Necessary and Sufficient Conditions for Consensus in Third Order Multi-Agent Systems

Chi Huang,Member,IEEE,Guisheng Zhai,Senior Member,IEEE,and Gesheng Xu

Abstract—We deal with a consensus control problem for a group of third order agents which are networked by digraphs.Assuming that the control input of each agent is constructed based on weighted difference between its states and those of its neighbor agents,we aim to propose an algorithm on computing the weighting coefficients in the control input.The problem is reduced to designing Hurwitz polynomials with real or complex coefficients.We show that by using Hurwitz polynomials with complex coefficients,a necessary and sufficient condition can be obtained for designing the consensus algorithm.Since the condition is both necessary and sufficient,we provide a kind of parametrization for all the weighting coefficients achieving consensus.Moreover,the condition is a natural extension to second order consensus,and is reasonable and practical due to its comparatively decreased computation burden.The result is also extended to the case where communication delay exists in the control input.

I.INTRODUCTION

THERE has been great interest in cooperative control of multi-agent systems,where all agents are connected by a network(described by a graph),and they communicate to neighbor agents for necessary information such that the whole group can achieve a collective behavior.The specification for collective behavior includes flocks and swarms,sensor fusion,random networks,synchronization of coupled oscillators,formation control of multi robots,optimization-based cooperative control,etc.For more detailed information,see the cornerstone paper[1],the survey paper[2],the book[3],[4]and the references therein.

One important control problem in cooperative control is the consensus problem,which involves reaching an agreement regarding a certain quantity of interest that depends on the states of all agents.There are many important papers which have made great contributions in consensus problems for selforganizing networked systems[5]-[8].For networked secondorder integrators,[9]presented a necessary and sufficient condition for achieving consensus,where it is shown that both real and imaginary parts of the eigenvalues of the Laplacian matrix of the corresponding network play key roles.Recently,[10]presented a necessary and sufficient condition for consensus among second-order controllable canonical multi-agent systems.Both[9]and[10]dealt with communication delay in the discussion.The consensus problem of third-order nonlinear multi-agent systems with a fixed communication topology was discussed,and a consensus algorithm was proposed with several sufficient conditions in[11].For consensus control of higher order linear systems,a sufficient and necessary condition was obtained in[12]where the local control input included two parts:a feedback controller and the interactions from the neighbors.The interconnection graph considered in[12]is undirected,and thus,the discussion can not be extended to directed interconnection cases.Moreover,an approach of achieving consensus for more general linear agents in the framework of matrix inequalities and stabilization was proposed in[13],and the extension to the consensus problem for networked nonholonomic systems was dealt with in[14].For multi-agent systems with switching interconnection graphs,[15]adopted a combination of connected and disconnected graphs to achieve desired consensus,where the basic idea was inspired by switched systems analysis.

The main purpose of this paper is to extend the results in[9]and[10]to third order agents networked by directed interconnection graphs,that is,to provide a necessary and sufficient condition to design a consensus algorithm for a group of agents described by third order integrators.The motivation of dealing with third order agents is not only from theoretical interest but also from the fact that there are many real systems which are described by third order differential equations;for example,the location of bouncing robots,road vehicles with random terrain,and aircrafts in the wind[16],[17].A typical example is a mass-spring-damper system with jerk term[16],[17]whose dynamics is described by x(3)=-ax(2)+(x(1))2-x.Third order integrators are the simplest third order linear systems,and they exist in real systems such as electronic circuits(shown later in Remark 1).Since single or double integrators are typically used in consensus control in the literature,we choose to focus on third order integrators in this paper.

As in the literature including[9]and[10],we assume here that the control input of each agent is constructed based on the weighted difference between its states and those of its neighbor agents,in a decentralized manner,and aim at proposing an algorithm for computing the weighting coefficients in the control input.The problem is reduced to design a thirdorder Hurwitz polynomial with real or complex coefficients.It is noted that the direct computation method in[9]and the frequency domain test approach in[10]can not be applied directly and effectively to design the third-order polynomial with complex coefficients.For that purpose,we propose to adopt the generalized Hurwitz condition[18]in our design,and obtain a necessary and sufficient condition for the consensus algorithm design.Since the obtained condition is both necessary and sufficient,we provide a kind of parametrization for all the weighting coefficients(feedback gains)achieving consensus.Moreover,the condition turns out to be a natural extension to second order consensus,and is reasonable and practical due to its comparatively decreased computation burden.The discussion is extended to the case where communication delay exists in the control input.With the same control gains as in the case without delay,we aim to establish a tight upper bound for the delay as a necessary and sufficient condition such that consensus is maintained when involving communication delay.It is noted that the method of discussing delay in the Hurwitz polynomial is encouraged and revised from that in[10].Moreover,although the main idea and approach are different,we would like to mention that there have been many references discussing communication delays in consensus control of networked agents[19]-[23].

The remainder of this paper is organized as follows.In Section II we give some preliminary information about graph theory and provide two lemmas for the benefit of discussion later.Section III is devoted to describe the system of networked agents with the control input protocol including three design parameters,and to reduce the control problem to designing Hurwitz polynomials with complex coefficients.Then,Section IV gives a detailed discussion on the design of third-order Hurwitz polynomials together with some possible simplification and generalization.Furthermore,the extension to the case of control input with communication delay among agents is made in Section V,where a tight upper bound is established for the delay such that the desired consensus is maintained when the real communication delay is smaller than the bound.Two numerical examples are given in Sections IV and V to show effectiveness of the results.Finally,Section VI concludes the paper.

II.PRELIMINARIES

Let us first review some basic definitions for graphs and consensus in network of multi-agents.The interconnection of a family of agents can be represented by using a directed graph(or digraph)G=(V,E)with the sets of nodes V={1,...,N}and edges E⊂V×V.The edge(i,j)∈E or i→j means that the information of the ith agent is available for the jth agent.The neighbor agents set of the ith agent is defined aswhich is the index set of the agents from which the ith agent can obtain necessary information.

A directed path is a sequence of ordered edges,and a digraph is called strongly connected if there is a directed path from every node to every other node.A directed tree is a digraph,where every node,except the root,has exactly one parent.A spanning tree of a digraph is a directed tree formed by graph edges that connect all the nodes of the graph.We say that a digraph has(or contains)a spanning tree if there exists a spanning tree that is a subset of the graph.It is known that the condition that a digraph has a spanning tree is equivalent to the case that there exists a node having a directed path to all other nodes.

The Laplacian of a graph is defined as L=[lij]N×N,where

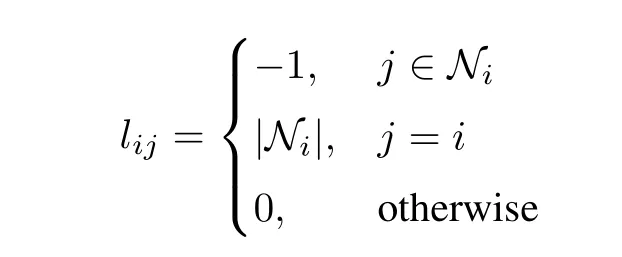
and|Ni|denotes the number of neighbors of the ith agent.It is easy to see from the above definition that all row-sums of a graph Laplacian L are zero,and thus L always has a zero eigenvalue and a corresponding(right)eigenvector 1=[1 1...1]T,satisfying L1=0.Furthermore,it is known that rank(L)=N-1 if and only if the graph has a spanning tree.For other spectral properties of graph Laplacians,see for example[24].

The next two lemmas will be used in the following sections.

Lemma 1[25]:Suppose A and D are square matrices.Consider the determinant of the block matrix

1)If|A|/=0,then|W|=|A|×|D-CA-1B|

2)If|D|/=0,then|W|=|D|×|A-BD-1C|

3)If AC=CA,then|W|=|AD-CB|

4)If BD=DB,then|W|=|DA-BC|.

Lemma 2[25]:Let A1∈ Rn1×n1,A2∈ Rn2×n2and A3be arbitrary.Then,the following properties of the Kronecker product hold:

1)A1⊗A3+A2⊗A3=(A1+A2)⊗A3

2)|A1⊗A2|=|A1|n2|A2|n1.

III.PROBLEMFORMULATION

Consider a group of networked third order agents whose dynamics are described by

where yi(t)∈Rmis generalized coordinate of the ith agent,and ui(t)∈Rmis the control input.Let the Laplacian of the interconnection graph be denoted by L.To consider consensus among the agents,we assume that there is a spanning tree in the graph,and thus rank(L)=N-1.Throughout this paper,we assume that the eigenvalues of L are µ1=0,µ2/=0,...,µN/=0.

Define

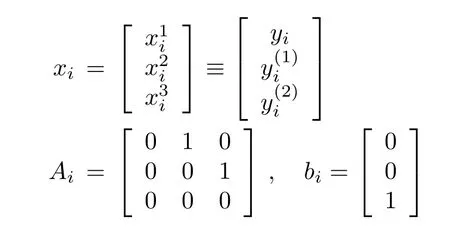
and rewrite the system as

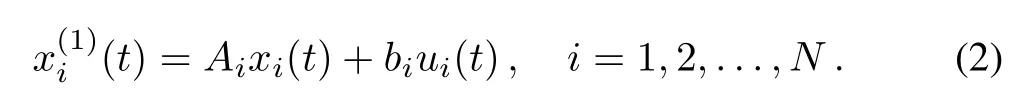
As in the literature,we assume that the available information for the ith agent is the states of itself and the neighboring agents,i.e.,xiand{xj:j∈Ni}.Then,the control problem is to design ui(t),using the available information,such that the consensus is achieved among all agents,that is,

Note that the consensus problem is different from the stabilization one in the sense that convergence to an equilibrium point such as the origin is not desired.In real systems,we usually do not want the system state to stop but rather,to track each other in a flexible manner.Therefore,even if the pair(Ai,bi)is controllable and we can use a local state feedback ui=Kixito drive the state to zero,the consensus control of achieving(3)is significant.

Similarly to the literature such as[9]and[10],we adopt the control input(consensus protocol)given by

where γ1,γ2and γ3are design parameters to be determined.

Remark 1:It is noted that the formulation of the third order integrator model in(1)is reasonable in two aspects.First,there are real examples that are described by third order integrators especially in electronic circuits.For example,consider a parallel circuit composed of an inductor(L)and a capacitor(C).If the variable y is the electronic charge on the inductor,and the control input u is the current in the capacitor,then we use Kirchhoff’s law to obtain u=CV(1)=C(Ly(2))(1),or equivalently,which is exactly a third order integrator.

Secondly,in the case that the dynamical equation of each agent is given by the more general form

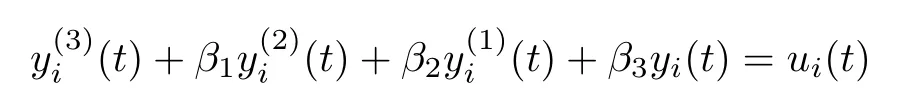
since it is reasonable to assume that each agent can obtain all states of itself,we define ui(t)=i(t)+(t)+(t)+β3yi(t)to obtain(t)=¯ui(t),which is exactly the third order integrator model(1).Then,as a result,we modify the control input(4)as

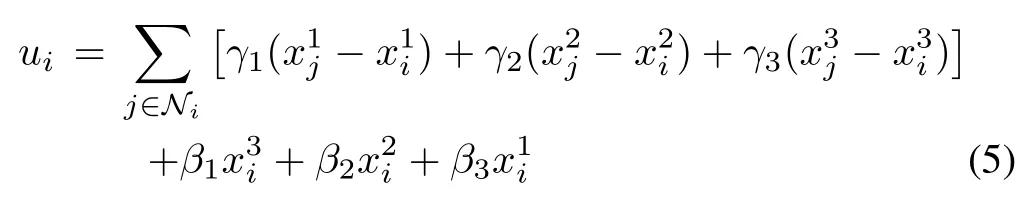
with the same design parameters γk’s.The remaining discussion is completely the same.

Remark 2:Although in this paper we focus our attention on third order agents for notation simplicity,as can be seen later,it is easy to extend the discussion to higher order integrators described by

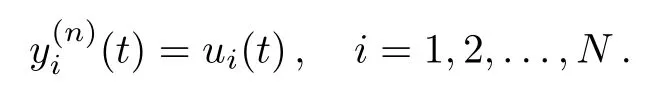
In this case,the matrices Aiand biare

The closed-loop system composed of the system(1)(or the system(2))and the controller(4)is

where

and

According to Lemma 2,we obtain that the characteristic polynomial is

Then,using the same technique as in[4],[9]and[10],the following fact can be proved easily.

Lemma 3:Consensus is achieved in(1)with(4)if and only if Θ has exactly three zero eigenvalues and all others have negative real parts.

According to Lemma 3,our design problem is to choose γ1,γ2and γ3such that Θ has three zero eigenvalues and all others have negative real parts.To proceed,we need the following lemma to analyze the spectral property of Θ.

Lemma 4:The characteristic equation of Θ is

Furthermore,if the eigenvalues of L are µ1,...,µN,then

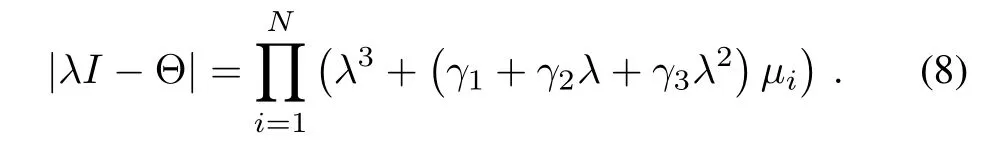
Proof:Using the definition of matrix eigenvalues,the characteristic equation of Θ is computed as

In the case of λ=0,we have

which is consistent with(7)with λ=0.

In the case of λ/=0,we use 1)of Lemma 1 to obtain

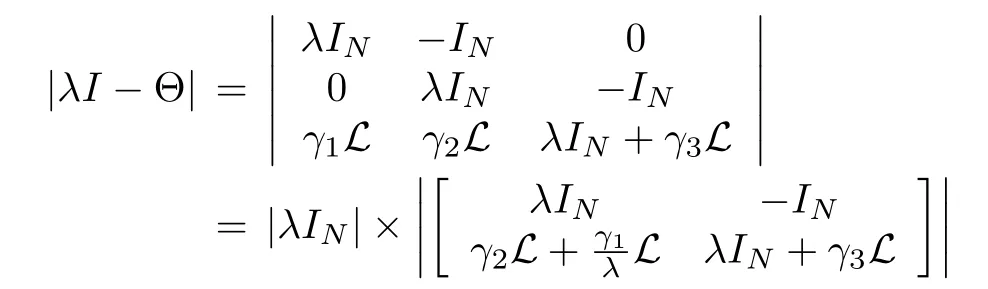
and,by 3)or 4)of Lemma 1,

This completes the proof of(7).

Next,when the eigenvalues of L are µ1,µ2,...,µN,the eigenvalues of-L are-µ1,-µ2,...,-µN,which leads to

and thus

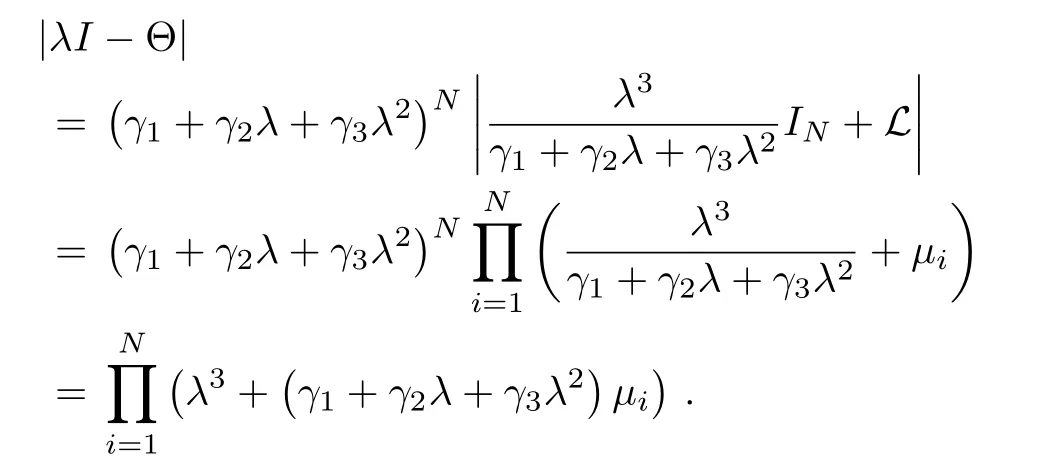
It is observed from the above thatµ1=0 corresponds to three zero eigenvalues of Θ.Therefore,according to Lemma 3,our design problem is reduced to choosing γ1, γ2and γ3such that the zeros of

have negative real parts for allµ= µi,i=2,...,N. ¥

Remark 3:Although the approaches in[9]and[10]are efficient in analyzing second order Hurwitz polynomials,they can not be used to design the third order polynomial pµ(λ).More precisely,the method in[9]needs to solve the characteristic equation with parameters,which is difficult for third equations.The design procedure in[10]is based on a frequency domain test for Hurwitz polynomial where it is required to check whether a polynomial pair is interlaced or not,which is also difficult in the present case.

IV.DESIGN OFCONSENSUSPROTOCOL

In this section,we discuss how to design the parameters γ1,γ2and γ3in the consensus protocol(4)such that the zeros of pµ(λ)have negative real parts for allµ = µi,i=2,...,N.

A.Approach Using Real Hurwitz Polynomials

Notice that whenµiis a nonzero complex eigenvalue of L,is also an eigenvalue of L.In addition,

is a polynomial with real coefficients.Then,based on the discussion in Section III,we have the following result.

Lemma 5:Suppose L has one zero eigenvalueµ1=0,s-1 nonzero real eigenvalues µ2,...,µs,and 2p complex eigenvalues σ1,,...,σp,p(s+2p=N).Then,consensus is achieved if and only if all pµi(λ)(2 ≤ i ≤ s)and(λ)(1≤j≤p)are real Hurwitz polynomials with respect to λ.

Forµi=ai＞ 0(2≤ i≤ s),

The Hurwitz matrix of pµi(λ)is

and thus,the necessary and sufficient condition for the zeros of pµi(λ)to have negative real parts is

Solving these inequalities,we reach

which gives a simple and explicit condition for the parameters.

However,for σj=bj+(bj＞0,1≤j≤p),which is not real,the degree of(λ)is 6.Then,if we apply the Hurwitz matrix condition under which the zeros ofhave negative real parts,we will obtain very complicated inequalities which are not practical.

B.Approach Using Complex Hurwitz Polynomials

To overcome the computational difficulty mentioned in the above subsection,we choose to consider the zeros of each pσj(λ)and p¯σj(λ)separately.Fortunately,since

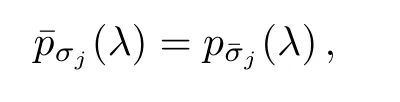
zeros of pσj(λ)are conjugate to those of.Using this fact,we can rewrite Lemma 5 by using Hurwitz polynomials with complex coefficients.

Lemma 6:Suppose L has one zero eigenvalueµ1=0,s-1 nonzero real eigenvalues µ2,...,µs,and 2p complex eigenvalues,...,(s+2p=N).Then,consensus is achieved in(1)with(4)if and only if all pµi(λ)(2 ≤ i≤ s)and pσj(λ)(1 ≤ j ≤ p)are complex Hurwitz polynomials with respect to λ.

To use the above lemma for consensus parameters design,we need the condition under which a polynomial with complex coefficients is Hurwitz.

Lemma 7[18]: The polynomial p(z)with complex coefficients,

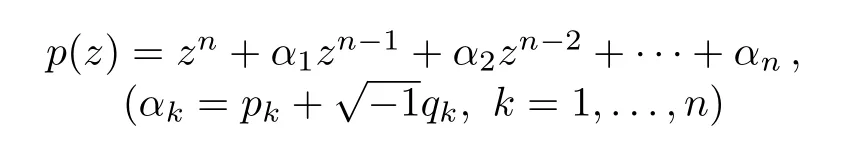
has all its zeros in the left half-plane if and only if the next determinants are all positive.

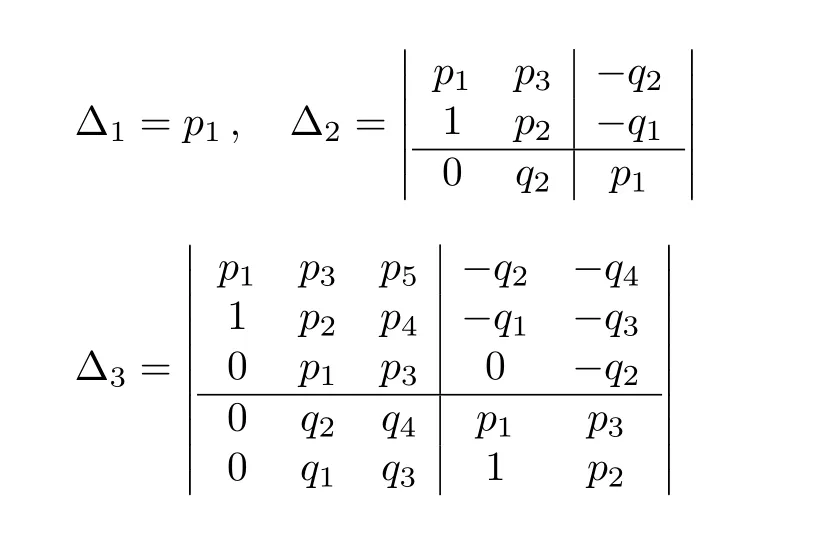
Using the above lemma for

where p1= γ3bj,q1= γ3cj,p2= γ2bj,q2= γ2cj,p3=γ1bj,q3= γ1cjin p(z),we obtain that the polynomial pσj(λ)has all its zeros in the left half-plane if and only if

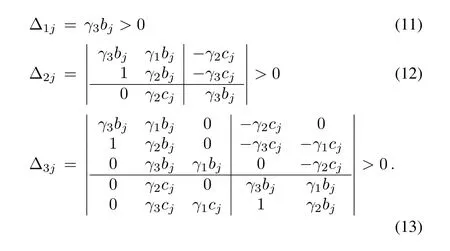
Since bj＞ 0,the condition(10)requires γ3＞ 0.Concerning(12),we obtain after simple calculation that

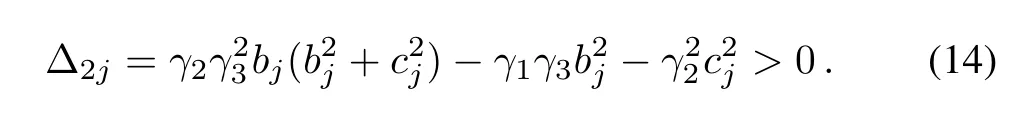
Next,we try to simplify the computation of Δ3j.Using the property of determinants(exchange the 3rd and the 4th row,and then exchange the 3rd and the 4th column),we obtain

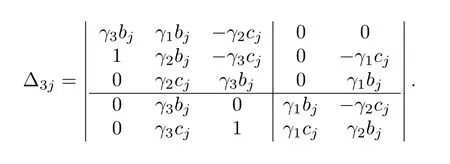
Notice that the leading principal minor of order 3 in Δ3jis exactly Δ2j,and thus Δ2j＞ 0 results in

Then,using 1)of Lemma 1,we obtain after some manipulation that

It is noted here that cjappears in Δ2jand Δ3jin the form of,and thus pσj(λ)and p¯σj(λ)have the same Δ2jand Δ3j,which is reasonable since their zeros have the same real parts.

Moreover,the above discussion is also valid for real eigenvalues,i.e.,cj=0.In this case,σj=bj,Δ1j= γ3bj＞ 0 requires γ3＞ 0,and requires thatwhich is the same as the final inequality in(10).And,

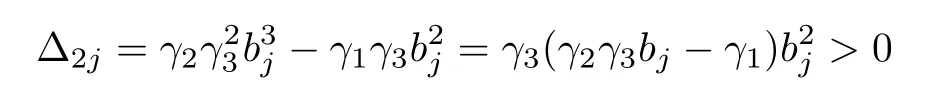
leads to γ1＞ 0,which appears in the first inequality of(10).

We summarize the above discussion in the following theorem,where we treat all the nonzero eigenvalues of L in a unified manner.

Theorem 1:Suppose that the Laplacian matrix L has the eigenvalues µ1=0,µ2/=0,...,µN/=0,and the real parts and imaginary parts of nonzeroµjare bjand cj,respectively.Then,consensus is achieved in(1)with(4)if and only if the parameters γ1,γ2,and γ3are chosen to satisfy

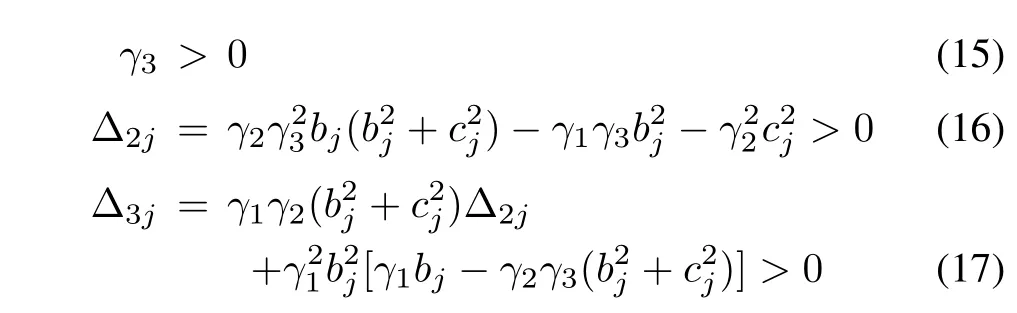
for all j=2,...,N.

As mentioned in the above,when the Laplacian matrix only has real eigenvalues(including the case of undirected interconnection among agents),the inequalities(15)-(17)shrink into(10).Since the condition(10)is much simpler to implement,we state the following corollary.

Corollary 1:Suppose that the Laplacian matrix L has only real nonzero eigenvaluesµj＞ 0,j=2,...,N.Then,consensus is achieved in(1)with(4)if and only if γ1,γ2,and γ3are chosen to satisfy

C.Discussion on Computation of Parameters

When the Laplacian matrix L has only real eigenvalues,the condition(18)is straightforward and thus the design of parameters γi’s is easy.However,when there are complex eigenvalues,it is not an easy task to choose parameters satisfying(16)and(17).Although γ3＞ 0 has been obtained in(15),we can not determine whether γ1and γ2are positive or not,if L has no nonzero real eigenvalues.Fortunately,the answer to this question is solved in the following theorem.

Theorem 2:Suppose that the Laplacian matrix L has the eigenvalues µ1=0,µ2/=0,...,µN/=0.Then,with the control input(4),the necessary condition for achieving consensus in(1)is γ1＞ 0,γ2＞ 0 and γ3＞ 0.

Proof:Consensus in(1)with(4)is achieved if and only if the conditions(15)-(17)are satisfied.γ3＞ 0 has been obtained in(15),and the remaining task is to show γ1＞ 0,γ2＞ 0.

First,we obtain from the definition of Δ2jthat

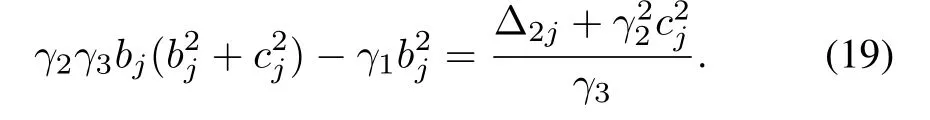
Substituting(19)into Δ3jin(17),we have

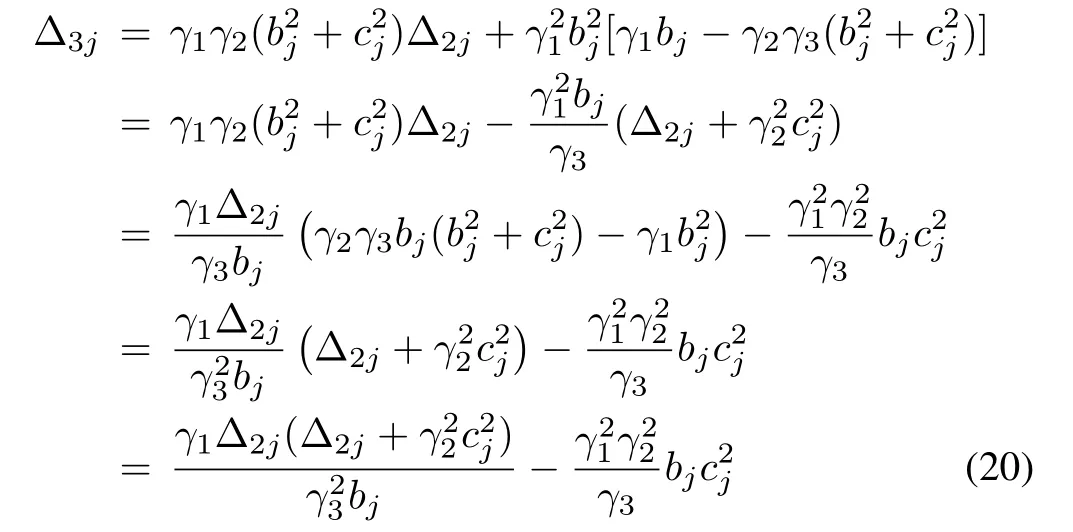
which is equivalent to

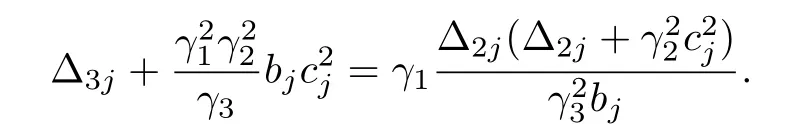
Since γ3＞ 0,bj＞ 0,Δ2j＞ 0 and Δ3j＞ 0,one easily obtains γ1＞ 0 from the above equation.

Next,rewriting(19)into

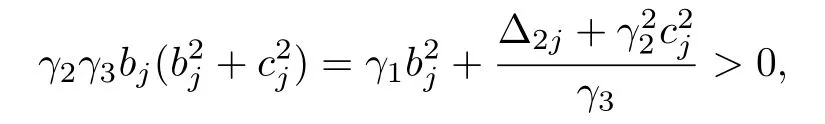
we get γ2＞ 0 easily. ¥

The above theorem shows that the parameters have to be positive.In addition,we shall show that the conditions(16)and(17)may be combined to compute the solution.Since(20)is equivalent to

our problem is reduced to solving

together with Δ2j＞ 0,with respect to positive parameters γ1,γ2,γ3.Furthermore,we obtain from(21)that

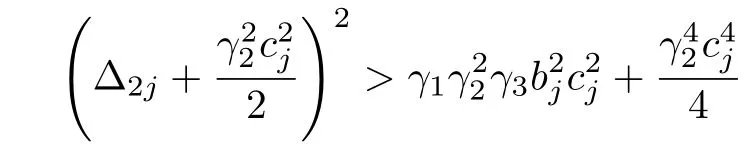
and thus

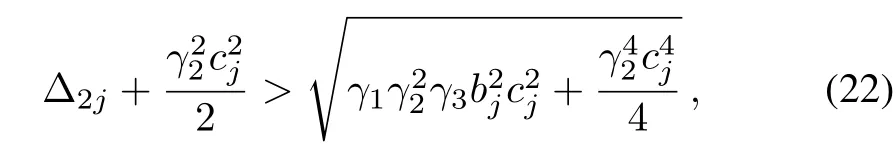
which guarantees Δ2j＞ 0.

Substituting Δ2jin(16)into(22)and summarizing the above discussion,we obtain the following result.

Theorem 3:Suppose that the Laplacian matrix L has the eigenvalues µ1=0,µ2/=0,...,µN/=0,and the real parts and imaginary parts of nonzeroµjare bjand cj,respectively.Then,consensus is achieved in(1)with(4)if and only if the parameters γ1,γ2,and γ3are chosen to be positive and satisfy

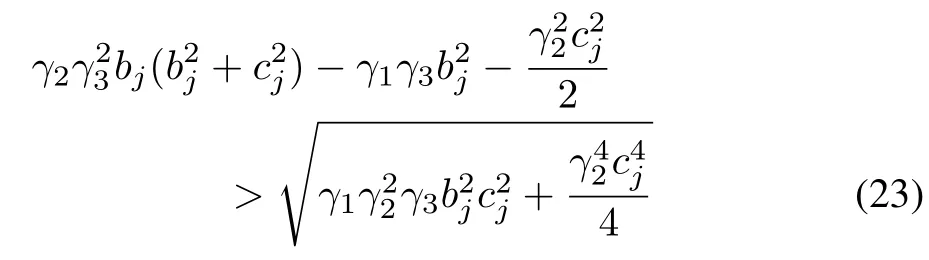
for all j=2,...,N.

Remark 4:Although(23)is a nonlinear and complicated inequality,we can analyze it efficiently to design the parameters.Firstly,when all cj’s are zero(the case where L has only real eigenvalues),(23)shrinks into γ2γ3bj＞ γ1,which again is the same as in(10).Secondly,when there are nonzero cj’s,given positive γ1,γ3,we see easily from(23)that γ2can not be very large due to the termon both sides of(23),and we can evaluate an upper bound for γ2such that(23)is satisfied.Moreover,(23)does not hold when γ2→ 0,and thus,there is a lower bound for γ2.Therefore,we can first fix positive parameters γ1,γ3,to evaluate the upper bound and lower bound for γ2,i.e.,

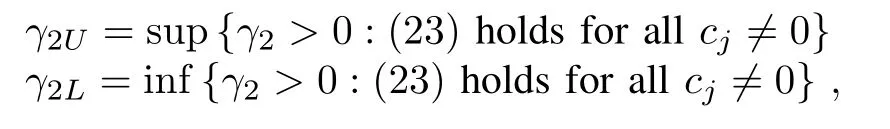
and then choose γ2satisfying γ2L＜ γ2＜ γ2U.

There are many practical tools for evaluating γ2Land γ2U.For example,one can numerically solve the nonlinear equations

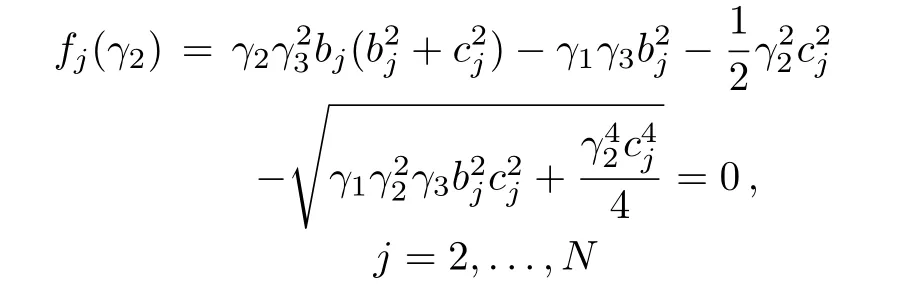
by using bisection,the Newton method or other numerical algorithms.

D.Numerical Example

In the end of this section,we give an example for the consensus algorithm proposed above.

Example 1:Consider 5 agents connected as in Fig.1,which is a directed graph.Then,N=5 and the Laplacian of the network is

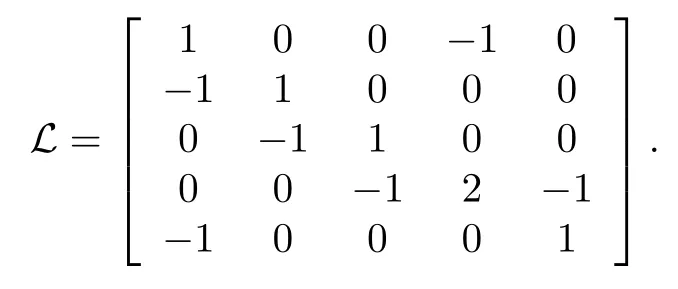
The eigenvalues of L areµ1=0,µ2=1,µ3=2,σ1,2=In correspondence with the notations we used,let aandThen,for the real eigenvalues,we obtain from(18)that

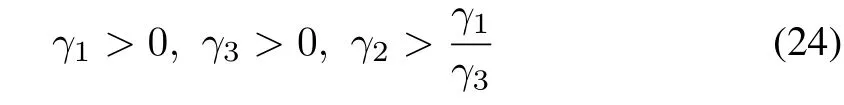
and for the complex eigenvalues we have

and

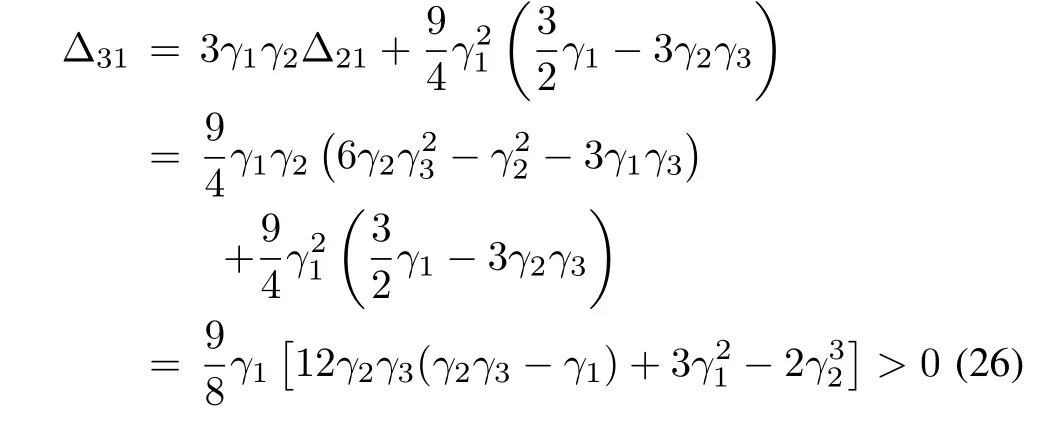
Fig.1.Five agents networked by directed graph(Example 1,2).

On the other hand,the inequality(23)turns out to be

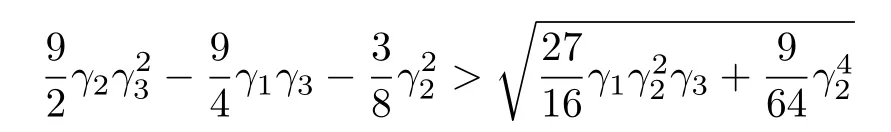
or equivalently,

It is easy to observe that there are infinite solutions to the simultaneous inequalities(24)-(26)or(27).For example,

is one solution.

Using the consensus algorithm(4)with these parameters,the plots of the systems’trajectories are depicted in Fig.2,where the initial conditions are

It can be observed that consensus has been achieved.

Fig.2. States of five agents achieving consensus(Example 1,γ1=1,γ2=1,γ3=2).

On the contrary,if we choose the parameters

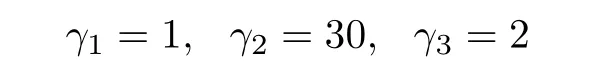
then(26)and(27)are not satisfied.With the same initial conditions,the plots of the systems’trajectories are depicted in Fig.3,and consensus has not been achieved.

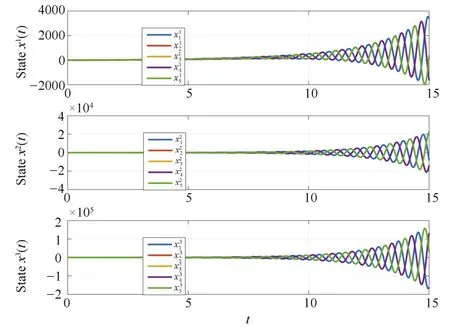
Fig.3.States of five agents not achieving consensus(Example 1,γ1=1,γ2=30,γ3=2).

V.CONSENSUSWITHCOMMUNICATIONDELAY

In this section,we assume that the design parameters γ1,γ2and γ3have been designed so that the conditions in Theorem 1 are satisfied,and analyze the period of time delay that the proposed algorithm can tolerate.In the case of constant communication delay,the control input takes the form of

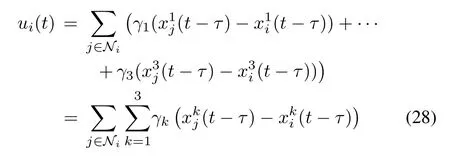
where τ≥0 is the constant time-delay.Then,the system(1)with the above control input can be rewritten in the compact form

where

Similarly to the discussion in Lemma 4,the characteristic polynomial of the above system is

and thus the characteristic equation is dominated by

Then,consensus is achieved if and only if the above equation has exactly three zero eigenvalues and all other eigenvalues have negative real parts.

Let pµi(λ,τ)= λ3+(γ1+ γ2λ + γ3λ2)e-λτµi,then?

We see from the above thatµ1=0 corresponds to zeros of pµ1(λ,τ)=0,which are three zero eigenvalues as before.

Next,we seek the condition about the communication delay τ,under which each pµi(λ,τ),2 ≤ i ≤ N,has zeros with negative real parts.The main idea is motivated and revised from the discussion in[10].First,observe that the quasipolynomial pµi(λ,τ)is Hurwitz stable when τ =0 and unstable for some large positive τ.Thus,there exists a positive upper bound τifor τ such that pµi(λ,τi)has a zero on the imaginary axis and it remains Hurwitz stable for any delay smaller than τi.Therefore,the problem is reduced to finding the smallest τifor i=2,...,N such that one of pµi(λ,τi)’s has imaginary roots.

For this purpose,we substitute∈ R,ωi/=0)into pµi(λ,τi)=0 to obtain

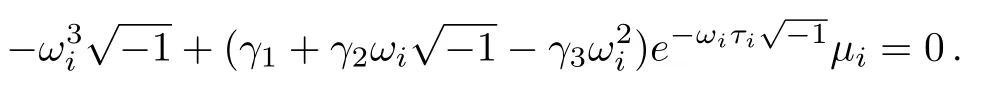
Separating the real and imaginary parts of the above yields

where

Then,it is easy to reach

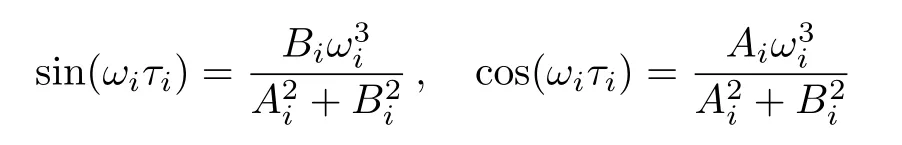
where

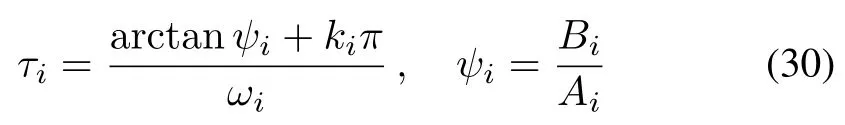
and kiis the minimum integer such that τi＞ 0,i=2,...,N.

Using sin2(ωiτi)+cos2(ωiτi)=1 in(29),we obtain

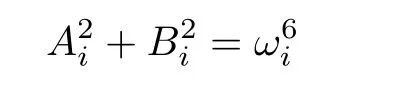
and after simple calculation,

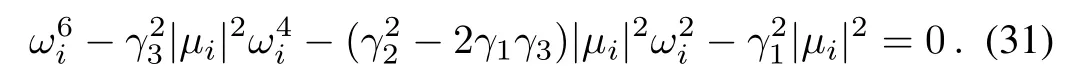
The procedure of calculating the upper bound τ∗is summarized as follows:

1)Forµi/=0(2≤ i≤ N),solve(31)to obtain the positive solution ωi.

2)Calculate Ai,Biand then τias in(30).

3)Let τ∗=min2≤i≤N{τi}.

Theorem 4:Suppose that the parameters γ1,γ2and γ3have been designed such that the third order multi-agent system(1)has achieved consensus with the algorithm(4).The system(1)with communication delay τ,i.e.,with the control input(28),achieves consensus if and only if τ＜ τ∗=min2≤i≤Nτi.

Example 2:Consider the multi-agent system used in Example 1.The nonzero eigenvalues of L areµ2=1,µ3=2,Moreover,assume γ1=1, γ2=1, γ3=2 have been chosen such that the consensus is achieved when no communication delay is involved.

Next,we compute τifor nonzero eigenvalues µi.

1)Forµ2=1,(31)is

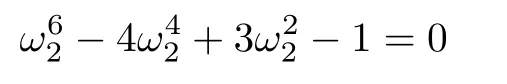
and its positive solution is ω2=1.7742.Correspondingly,A2=1.7742,B2=5.2958,and τ2=(tan-1)/ω2=0.7031.

2)Forµ3=2,(31)is

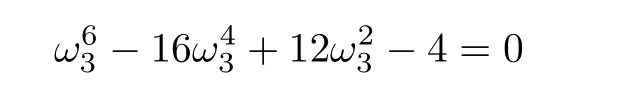
and its positive solution is ω3=3.9025.Correspondingly,A3=7.8049,B3=58.9172,and0.3688.

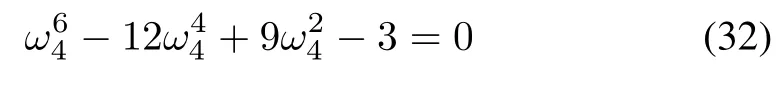
and its positive solution is ω4=3.3499.Correspondingly,A4=-13.5459,B4=35.0665,andπ)/ω4=0.5790.

Therefore,τ∗=min{τ2,τ3,τ4,τ5}=0.2663.

Using the same initial condition as in Example 1,Fig.4 shows that consensus has been achieved when τ=0.25,while Fig.5 shows that consensus can not be achieved when τ=0.27.

Fig.4. States of five agents achieving consensus(Example 2,γ1=1,γ2=1,γ3=2,τ=0.25).

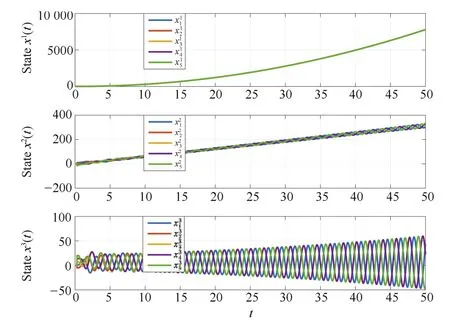
Fig.5.States of five agents not achieving consensus(Example 2,γ1=1,γ2=1,γ3=2,τ =0.27).

VI.CONCLUDINGREMARKS

In this paper,we have considered the consensus algorithm for networked third order agents,and have established a necessary and sufficient condition(protocol)for designing the parameters in the control input.The key idea is to reduce the consensus problem into designing a Hurwitz polynomial with complex coefficients.The main result turns out to be a natural extension from second order consensus,and it does not require large computational efforts.Moreover,the discussion has also been extended to the case where a constant communication delay exists in the control inputs.A tight upper bound for the delay has been established as a necessary and sufficient condition under which consensus is maintained when communication delay is involved.