Speed-assigned Position Tracking Control of SRM With Adaptive Backstepping Control

Jiajun Wang

Abstract—A novel speed-assigned method is applied to the position tracking control of switched reluctance motor(SRM).A speed control freedom can be drawn into the position control through speed assignment.Adaptive backstepping control is used to design the position controller for the SRM.The accuracy of position tracking of the SRM can be enhanced with speed assignment.A disturbance observer is further designed to enhance the estimation accuracy of the unknown load torque.Simulation results certify that the design scheme is right and effective.

I.INTRODUCTION

SWITCHED reluctance motors(SRMs)have the simplest and most robust construction among electric motors.Although SRMs have many good characteristics,the doublesalient and high saturated features result in strong nonlinearities.SRMs have never been a popular choice in highaccuracy position control due to the drawback of higher torque ripple compared with conventional motors.The torque ripple can cause large vibrations and acoustic noise[1].At present,almost all research on SRMs focus on speed or torque control[2].As an important application aspect,position control of the SRMs still has several problems which must be solved.This paper mainly focuses on solving three problems related to the position control of the SRM:how to enhance the accuracy of position tracking,how to depress torque ripple,and how to reduce the effect of unknown load torque.

Generally speaking,the position control of motors is composed of three control loops:position loop,speed loop,and current loop[3].As we know,in position control of SRMs,the motor speed is solely controlled by the output of the position loop.That is to say,the speed,which is the differentiation of the rotor position,can not be controlled independently.If one control freedom of motor speed can be added in the position control of the SRM,the position-control flexibility and accuracy of the SRM can be enhanced greatly.Adding this control freedom of speed in the position tracking control of the SRM is a key research problem that is discussed in this paper.

Tracking control is a widely researched problem in modern control theory,which can be divided into trajectory-tracking and path-following[4],[5].Trajectory-tracking is concerned with the design of control laws that force the states to reach and follow a time parameterized reference signal.Pathfollowing forces states to follow a specified path without any specific dynamic requirements along the path(such as the constraint of the time or speed).At present,all the position tracking control of the SRMs can be considered trajectory tracking control problems.In position tracking control of the SRMs,if the tracking speed can be controlled deliberately,then the performance of the tracking can be enhanced.The idea in this paper is to add a speed control freedom in the position tracking which originates from the path-following method in[5].

In position tracking control of the SRM,besides the speed control,the torque control performance also need to be considered.At low speed,the torque ripple has strong influence on the position tracking performance.To reduce the torque ripple of the SRM,different torque control techniques have been developed[6]-[8].In[6],the direct torque control(DTC)for the SRM was first proposed as the DTC in AC motor.In[7],direct instantaneous torque control(DITC)is used to realize the high-dynamic four-quadrant operation of the SRM.In[8],torque-sharing function(TSF)is adopted to reduce the torque ripple with torque sharing between different phases.The DTC and DITC can be considered as torque direct control.While the TSF can be considered as indirect torque control.It is of great convenience to use DTC to realize torque control.

There are many elements which affect the position tracking performance of the SRM.Unknown load torque is yet another element which should be considered.If the unknown load torque can be estimated,the position tracking performance can be enhanced further.Backstepping control technique is a systematic and recursive design methodology for nonlinear feedback control[9]-[11].The most appealing point of it is to use the virtual control variable to make the original highorder system simple,and the controller can be derived step by step.In this paper,the function of backstepping control is twofold.One is to realize the controller design of speedassigned position tracking,and the other is to estimate the unknown load torque of the SRM.

The disturbance attenuation problem of a nonlinear system has been investigated via a nonlinear model predictive control(MPC)method augmented with a disturbance observer[12].Disturbance observer has been popularly applied in the design of tracking controllers for motion control systems[13].Most of the work in the design of disturbance observer is engineering-oriented and lacks sound theoretical justification.In this paper,a disturbance observer is designed based on state equations,which can realize estimation of the unknown load torque.The designed disturbance observer can enhance the estimation accuracy of the load torque further compared with the adaptive estimation in the adaptive backstepping design.

The novelty of the paper can be mainly summarized as following four aspects.

1)The speed-assigned method is firstly used in the position tracking control of the SRM to enhance the accuracy of position tracking.

2)The adaptive backstepping control is successfully applied to the speed-assignment design of the SRM.The speed control freedom can be easily added in the position tracking control through the backstepping design.

3)The disturbance observer is utilized to realize the load torque estimation of the SRM,which can enhance the estimation accuracy of the load torque compared with the estimation strategy using the adaptive backstepping design.

4)The DTC is used to reduce the torque ripple of the SRM in the position tracking control.

The remainder of this paper is organized as follows.In Section II,the model of the SRM is given.In Section III,speed-assigned position tracking control is designed.In Section IV,the design of disturbance observer is given.In Section V,the simulation procedure is shown,and lots of simulation results are given to certify the rightness and effectiveness of the design.And finally,some conclusions are presented in Section VI.

II.MODEL OF THESRM

The model of the SRM can be referenced to[14]and given by the following state equations:

where θ is the rotor position,ω is the rotor speed,ikis the kth phase current,ukis the applied kth phase voltage,Tkis the kth phase torque,ψkis the kth phase flux-linkage,R is the phase resistance,B is the damping coefficient,Nphis the total phases of the SRM,J is the moment of inertia of the rotor,and TLis the load torque.The kth phase torque can be derived from the flux-linkage expression,and the total torque can be computed with.In this paper,Tkis derived from the experimental data and can be acquired through the lookup of a two-dimensional table.

To simplify the position tracking control of the SRM,the mechanical part is selected as the controlled part.The electromagnetic part is enclosed in the inner loop,which will be given in Section V.The simplified mechanical part are given as the following state equations:

where a=-B/J,b=1/J,d=-TLJ,u=Te.And d represents the uncertain part of the model.

Before the design of the position tracking control,we first give three assumptions.

Assumption 1:The load torque TLis assumed to be unknown to the controller.The uncertainty of the rotor inertia J and the viscous constant B are not considered.That is to say,J and B are assumed to be constants.

Remark 1:The load torque is considered as the only uncertainty to the controller design in this paper.If the uncertainties of J and B are considered,[15]can be referenced,which gave the solution for the uncertainties of J and B with the disturbance observer.

Assumption 2:Because the mechanical dynamics of the motor is slower than the electrical dynamics,the load torque of the SRM can be assumed to satisfy that=0[16].Then,it is reasonable to assume that=0.

Assumption 3:d is assumed to be estimable with.And

III.POSITIONCONTROLDESIGN OFSRM

A.Definition of Speed-assigned Position Tracking

Assumption 4:We assume that θdis the reference position signal of the SRM,and θdis two times differentiable.It is reasonable to assume that θd,˙θd,and¨θdexist and are bounded.

The general position tracking control can be called timeassigned position tracking control.Time-assigned position tracking control means to be at specific position along the reference signal at specific time instances.The time-assigned position tracking can be presented as following equation:

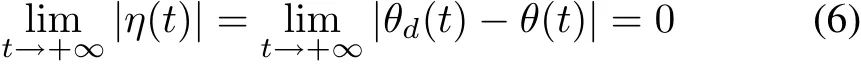
where η(t)is the tracking error.This means that the rotor position θ(t)of the SRM tracks the desired position θd(t)asymptotically.

In contrast to time-assigned control,speed-assigned control means to design a desired speed at specific position.If the reference position θd(t)is given as a time related function,it is a function of γ(t).That is to say the reference position signal is given as θd(γ(t)),where γ(t)is the function of time.One control freedom can be added to the position tracking control of SRM through this processing.The speed-assigned method can be realized if the following condition can be achieved[5].

where vd(θd(t),t)is the assigned speed at different position.Then it is reasonable to have the following condition:

To simplify the function presentation,we will use γ,vd,η,,to present γ(t),vd(θd(t),t),η(t),

B.The Design of Adaptive Backstepping Control

The design of the adaptive backstepping controller for speed-assigned position tracking of the SRM can be achieved through two steps.

Step 1:The position tracking error x1can be described as the following equation:

The time derivative of x1can be given as

According(10),the virtual variable x2is selected as

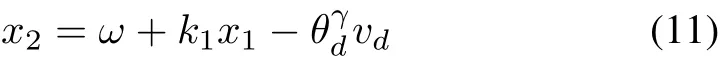
where k1is a positive constant,then the time derivative of x1can be written as

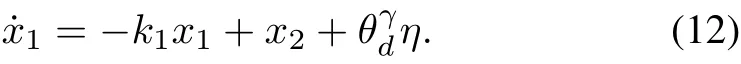
The first Lyapunov function V1is selected as the traditional form

The time derivative of Lyapunov function V1can be computed as

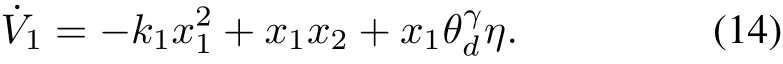
Step 2:The second Lyapunov function V2is designed as

The time derivative of the second Lyapunov function can be written as

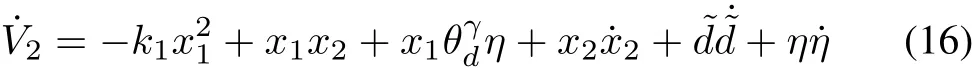
where the time derivative of x2can be derived from(11).The time derivative of virtual variable x2can be computed as

Until now,the control u can be designed as following equation:

where k2is a positive constant.The control rules for the load torque estimation errorand speed-assigned tracking error η should be designed as

where k3and k4are positive constants.With the control u,the errorand error η,the time derivative of the second Lyapunov function can be written as

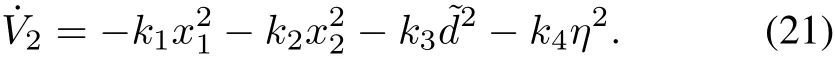
According to Barbalat’s Lemma[17],we can obtain＜0 when x1/=0,x2/=0,/=0 or η/=0.And then when＜0,V2→ 0 as t→ +∞.At last θ-θd→ 0 can be realized,and speed-assigned position tracking control of the SRM with an unknown load torque is achieved.

IV.THEDESIGN OFDISTURBANCEOBSERVER

The proposed control structure of SRM with the disturbance observer is given in Fig.1.As seen from the figure,the composite controller consists of two parts:a controller and a disturbance observer.In the position tracking control of SRM,the unknown load torque TLcan be estimated with the disturbance observer.

Fig.1.The control structure with the disturbance observer.

From Assumption 2,we can know=0.The disturbance observer can be designed as following state equation:

From the disturbance observer,we can obtain the estimated load torque,and=-

Theorem 1:Consider the model(4)and(5)of SRM with unknown load disturbance d.The disturbance observer(22)and(23)can converge to the disturbance d exponentially.

Proof:Combining the model(4)and(5)of SRM and the disturbance observer(22)and(23),the differentiation of˜d can be computed as following:

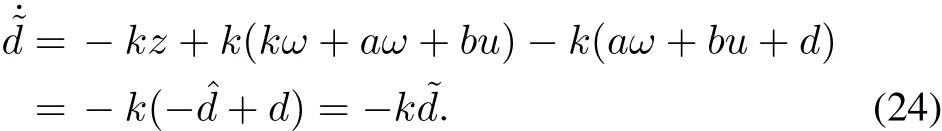
Equation(24)can be simplified as

The above disturbance observer has the following three advantages.

1)The design of the disturbance observer is very simple.It can enhance the disturbance attenuation ability of any control system with the same structure.

2)The disturbance observer is exponentially stable,and its stability is regardless of the design of the controller.This can enhance the flexibility of the controller design.

3)The disturbance observer can be designed before or after the controller design.It is very meaningful to simplify the control system design.This can be used for other control systems with the form described as(4)and(5).

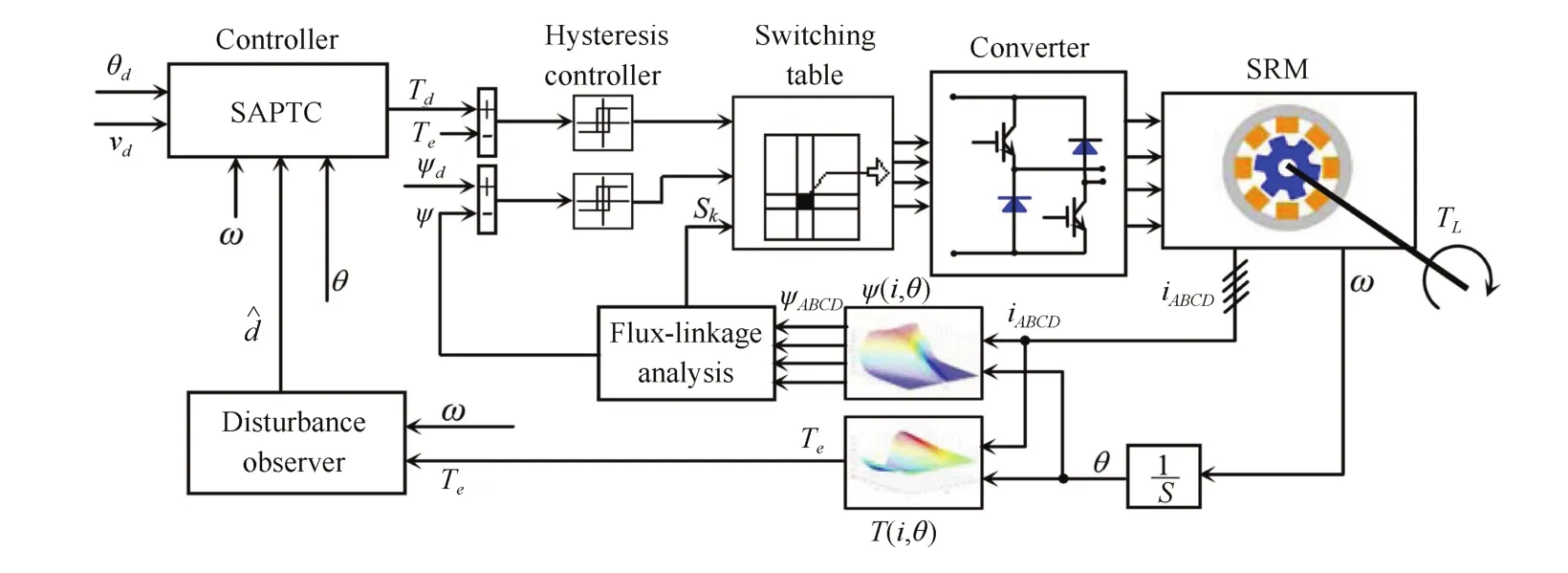
Fig.2.The control structure of the SRM system.

Fig.3.The measured electromagnetic torque and flux linkage.

V.SIMULATIONPROCEDURE ANDANALYSIS

The structure of speed-assigned position tracking control of the SRM is given in Fig.2.In Fig.2,the speed-assigned position tracking controller is abbreviated as SAPTC.The output of the SAPTC block u is the desired torque Td,which is compared with the feedback torque Te.Tecan be acquired with the rotor position and phase current through the lookup of the 2-D table of torque,which is obtained through experiment.The flux-linkage ψ can be computed from ψABCD,which is acquired from the experimental torque data.In torque andflux-linkage control loops,the hysteresis controller is used to control the torque and flux-linkage.The traditional asymmetric half-bridge converter is chosen as the voltage-supply unit for the SRM.The normal parameters of the SRM are given in Table I.

A.Data Acquisition of Electromagnetic Torque T(i,θ)and Flux-linkage ψ(i,θ)

1)Measurement of T(i,θ):The modeling of the electromagnetic torque and flux-linkage for SRM is still an open problem.There are no analytical models which can describe the performance of SRM completely.In this paper,the torque measurement data are first acquired from a measurement method proposed in[18].Then,the flux-linkage data are computed from the torque measurement data.From the experiment data,the relationship between the electromagnetic torque and the phase current and rotor position is given in Fig.3(a).

2)Computation of ψ(i,θ):The static flux-linkage profile can be computed from the measured static torque characteristics.The method can avoid errors introduced by the iron losses and copper losses of the SRM.To acquire the data offlux-linkage,the co-energy should be computed firstly.

TABLE I DATA OF THETESTEDSRM

The co-energy can be computed from the measured torque data at a constant current(I)and position θ0as in[18]

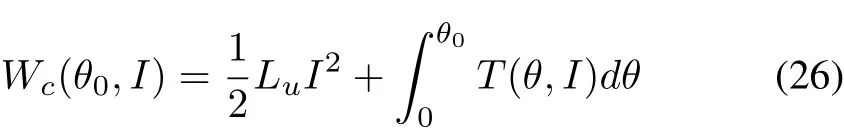
where Wc(θ0,I)presents the co-energy and Luis the inductance at the unaligned position(30◦).Then the flux-linkage can be computed from the co-energy as

where i is the phase current of the SRM.

To acquire the flux-linkage characteristics of the SRM,two steps of computation are needed.

1)The data of co-energy Wc(θ0,I)are first computed with(26)from the measured torque data.

2)The data of flux-linkage is acquired from the data of the co-energy Wc(θ0,I)with(27).The figure of flux-linkage ψ(θ,I)is given in Fig.3(b).

B.Realization of Direct Torque Control

Similar to induction motors,equivalent space voltage vectors may be defined for the SRM.The voltage space vectors for each phase are defined as lying on the center axis of the stator pole.The definition of the voltage space vectors for a four phase 8/6 SRM are shown in Fig.4(a).The voltage state definition of one phase of SRM are given in Fig.5.

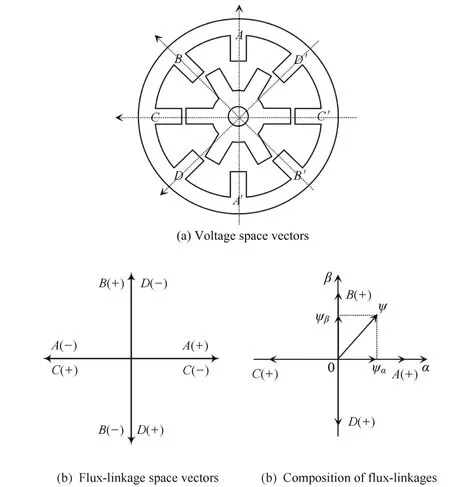
Fig.4.The definition of the voltage and flux-linkage vector.

Fig.5.The voltage state definition of one phase.

According to the eight effective voltage space vectors in Fig.4(a),the formation of flux-linkage directions are given in Fig.4(b).As in Fig.4(c),the relation between composite vector of flux-linkage and the phase flux-linkage vector are given as following equations:

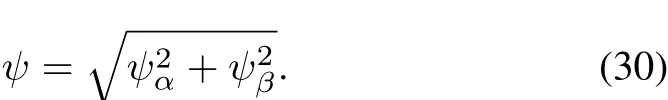
One of the eight possible states is chosen at a time in order to keep the stator flux linkage and the motor torque within hysteresis bands.The space distribution of eight effective voltage space vectors are given in Fig.6(a),where Sk,Uk(k=1,2,...,8)represent sectors and voltage space vectors,respectively.Whenever the stator flux linkage reaches its upper limit in the hysteresis band,it is reduced by applying voltage vectors which are forced toward the center of the flux vector space and vice-versa.This procedure is illustrated in Fig.6(b).

Fig.6.Effective voltage phase vectors.

C.Simulation Results and Analysis

In the simulation of the speed-assigned position tracking control of the SRM,there are five control variables that need to be regulated.The control variables are given as k=1200,k1=480,k2=7200,k3=1200,and k4=4500.

To test the effectiveness of the speed-assigned position tracking control of the SRM,four cases of simulation are given.The desired position reference signal is set as θd=sin(γ(t))rad.

In the first case of simulation,the assigned-speed of the SRM is set to be vd=8π rad/s.The load torque is given as a constant value TL=1Nm.The simulation results are shown in Fig.7.In Fig.7, “adaptive estimation”and “disturbance observer”present the control scheme with adaptive backstepping estimation and disturbance observer for the unknown load torque respectively.Fig.7(a)shows the reference position,actual position,and position tracking errors.Fig.7(b)demonstrates the assigned speed,actual speed,and the speed errors.And Fig.7(c)gives the actual load torque,estimated load torque,and estimated errors.

In the second case of simulation,the assigned-speed of the SRM is reduced to be vd=4π rad/s.The unknown load torque is given the same as the first case TL=1Nm.The simulation results are shown in Fig.8.

In the third case of simulation,the assigned speed of the SRM is set to be vd=8π rad/s.The unknown load torque is given as TL=1+0.5sin(10πt)Nm.The simulation results are shown in Fig.9.

In the fourth case of simulation,the assigned speed of the SRM is reduced to be vd=4π rad/s.The unknown load torque is given the same as the third case TL=1+0.5sin(10πt)Nm.The simulation results are shown in Fig.10.

The comparison between adaptive estimation and disturbance observer of the speed-assigned position tracking under different conditions are given in Table II and Table III,where the position error,speed error,and torque estimated error represent steady errors.And AE and DO present adaptive estimation and disturbance observer respectively.

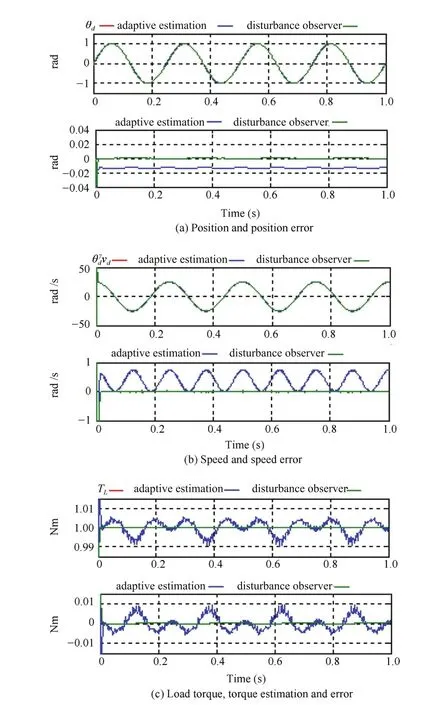
Fig.7.The simulation results of the first case.

TABLE II COMPARISONBETWEENADAPTIVEESTIMATION AND DISTURBANCEOBSERVERWHENTL=1Nm

TABLE III COMPARISONBETWEENADAPTIVEESTIMATION AND DISTURBANCEOBSERVERWHENTL=1+0.5sin(10πt)Nm

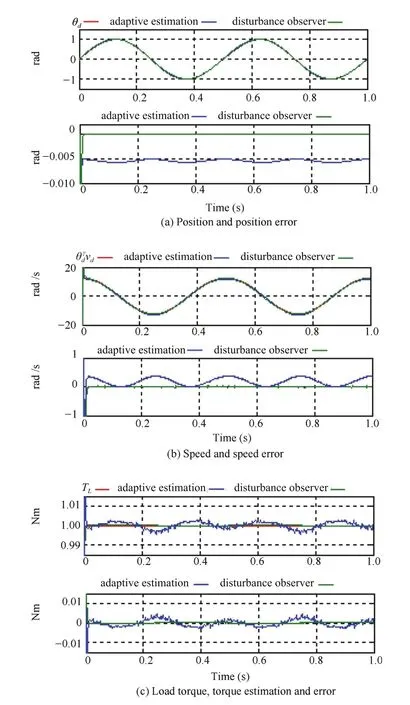
Fig.8.The simulation results of the second case.

To demonstrate the superiority of the proposed method,the speed-assigned position tracking control is compared with the traditional PID controller.The structure of the PID control for the SRM is given in Fig.11.Because the PID control does not need the load torque estimation and cannot realize the speed assignment,the load torque estimation and adaptive estimation units are omitted.

The parameters of the PID controller for the position control of the SRM are given as following:

In the simulation,the speed-assigned position tracking control of the SRM with disturbance observer is compared with the PID controllers.Two cases of the simulation results are given.The reference position and load torque are the same as the conditions in above two cases.The comparisons of the PID control and the speed-assigned position tracking control of the SRM with disturbance observer are given in Fig.12.Fig.12 shows the reference position,actual position,the tracking error with PID control,and speed-assigned strategy based on disturbance observer under different assigned speed.From the comparison,we can conclude that the speed-assigned position tracking with disturbance observer has higher tracking accuracy and better tracking dynamics than the traditional PID controller.

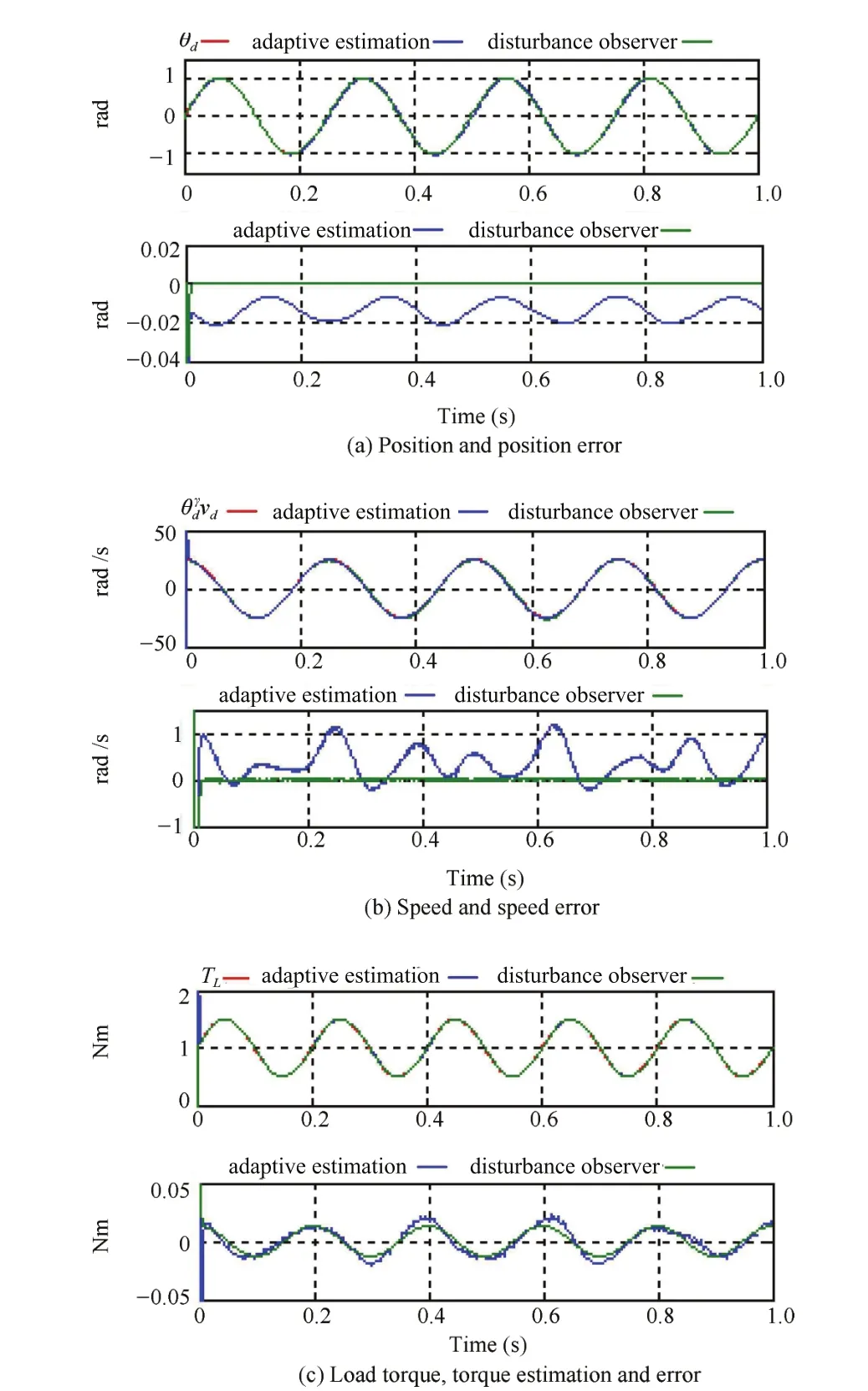
Fig.9.The simulation results of the third case.

From Figs.7-10,Fig.12 and Tables II and III given above for the speed-assigned position tracking,we can reach the following six conclusions.

1)The speed-assigned method can add a speed control freedom to the position tracking of the SRM.When a low speed is assigned to the position tracking,the position tracking error can be reduced.This is very meaningful for position control of SRM.

2)The disturbance observer can estimate the unknown load torque of the SRM.The convergent speed of the disturbance observer can be designed fast enough to suit the controller design.

3)The backstepping controller is effective for the speedassigned position tracking control of the SRM,and the controller has robustness for varying load torque.

4)The DTC has very good direct torque and flux-linkage control performance for the SRM.There is no need for the control of turn-on and turn-off angles.This is the virtue of the DTC to realize the four-quadrant operation of SRM.The transition procedure of SRM in four operating quadrants is very fluent.

5)The torque ripple of the SRM is reduced with combination of the DTC and disturbance observer.In the position tracking procedure,we can see that the torque ripple is small enough to realize the high accuracy of position tracking.

Fig.10.The simulation results of the fourth case.

6)The speed-assigned strategy is superior to the traditional PID control for the SRM.The speed-assigned position tracking control method has large potential for the position control of the SRM in the future.

VI.CONCLUSION

In this paper,a novel speed-assigned position tracking control of the SRM is designed which achieves excellent position control performance.The main contribution of this paper can be summarized as following three aspects.

1)A speed control freedom is successfully added to the position tracking control of the SRM.This can enhance theflexibility of position tracking control of the SRM.

2)The speed-assigned position tracking control of the SRM is realized with adaptive backstepping design.This design makes the speed-assigned error and load torque estimation an easy job.

3)The disturbance observer can enhance the accuracy of the load torque estimation.It is very meaningful for the position control of SRM.

The speed-assignment method proposed in this paper has a general applicability.The design method can be easily extended to the position control of other motors.

Fig.11.The structure of position control with PID control.

Fig.12.The comparison between PID controller and speed-assigned control with disturbance observer.