Optimal Decoupling Control Method and Its Application to a Ball Mill Coal-pulverizing System

Yue Fu,Chengwen Hong,and Jingyi Li

Abstract—The conventional optimal tracking control method cannot realize decoupling control of linear systems with a strong coupling property.To solve this problem,in this paper,an optimal decoupling control method is proposed,which can simultaneously provide optimal performance.The optimal decoupling controller is composed of an inner-loop decoupling controller and an outer-loop optimal tracking controller.First,by introducing one virtual control variable,the original differential equation on state is converted to a generalized system on output.Then,by introducing the other virtual control variable,and viewing the coupling terms as the measurable disturbances,the generalized system is open-loop decoupled.Finally,for the decoupled system,the optimal tracking control method is used.It is proved that the decoupling control is optimal for a certain performance index.Simulations on a ball mill coal-pulverizing system are conducted.The results show the effectiveness and superiority of the proposed method as compared with the conventional optimal quadratic tracking(LQT)control method.

I.INTRODUCTION

THE controlled objects of actual industrial processes are mostly multivariable.One of their important characteristics is the existence of couplings among the variables.That is to say,when one of the input variables of the object changes,many output variables or even all the output variables may change.Due to the existence of couplings among the variables,when the output variable of one control loop is changed by adjusting the controller parameters in the control loop,the output variables of the other control loops are also changed.This results in a degraded control effect,or even invalidity of the whole control system.Decoupling control system is one of the five advanced control systems in multivariable process control[1],whose research is very important.

Decoupling control methods are divided into open-loop decoupling control and closed-loop decoupling control.The open-loop decoupling control is realized in two steps.First,a decoupling compensator is designed,which transforms a multivariable system to multiple single-variable systems.Then,a controller is designed,which makes these single-variable control systems achieve the desired performance.By combining a decoupling compensator with a controller,the closedloop decoupling control is realized in one step.The coupling effect among the loops is reduced,and simultaneously the performance requirements are also achieved.

The earliest decoupling control method can be traced back to 1950s,where it was proposed for multivariable linear systems described by an input-output model.The decoupling control problem of multivariable linear systems described by a state space model was first proposed by Morgan in 1964.The sufficient and necessary conditions that a square system described by a state space model could be decoupled were given in[2].The decoupling control problem of nonsquare systems was solved in[3].For multivariable linear systems with unmeasurable states,the output feedback based decoupling control method was proposed in[4].There also exist other classical linear decoupling control methods,such as the inverse Nyquist matrix method[5],the Bristol-Shinskey method[6]and the related analysis method[7].

By the 1980s,linear multivariable adaptive decoupling control had become an important research field.Linear multivariable adaptive decoupling control methods are divided into open-loop adaptive decoupling control and closed-loop adaptive decoupling control.On the basis of identification,both of them use the conventional decoupling control method to decouple the system[8]-[10].

Since the 1990s,with the introduction of intelligent methods,nonlinear multivariable adaptive decoupling control has attracted the attention of control scholars and engineers.For a class of discrete-time multivariable systems with strong coupling,strong nonlinearity and uncertainty,the sufficient and necessary conditions that a system could be decoupled in a compact set were given in[11].In[12],the controlled system was linearized at an equilibrium point by using Taylor expansion,and then it was equivalently expressed as a combination of a linear model and a nonlinear higher order term.Based on the equivalent model,an adaptive decoupling control method was proposed by combining one step-ahead optimal weighting decoupling control with neural network feedforward compensation.In[13]and[14],the controlled system was transformed into a linear model with diagonal parameter matrices and a nonlinear term.By combining neural network feedforward compensation respectively with one stepahead optimal weighting adaptive control and generalized predictive adaptive control,two adaptive decoupling control methods were proposed.In the above literatures,the effectiveness of the proposed decoupling control methods are demonstrated only by numerical simulations.The stability and convergence of the closed-loop systems are not provided.To solve this problem,in[15]-[18],four adaptive decoupling control methods based on multiple models and neural networks were proposed by combining multiple model switching respectively with one step-ahead adaptive decoupling control,one step-ahead weighting adaptive decoupling control,adaptive generalized predictive decoupling control,and adaptive proportion integration differentiation(PID)decoupling control.The stability and convergence of the closed-loop systems were proved.In[19],the adaptive decoupling control method combining an open-loop decoupling compensator with neural network approximate compensation was proposed,which can also ensure the stability and convergence of the closed-loop system.For complex industrial processes with multivariable,strong coupling,strong nonlinearity and especially variable dynamic characteristics,two intelligent decoupling control methods were proposed by combining multiple model switching respectively with one step-ahead optimal weighting decoupling control based on neural network feedforward compensation and approximate dynamic decoupling control based on neural network feedforward compensation[20],[21].For nonlinear multivariable systems with unknown structures,an adaptive switching control method driven by virtual unmolded dynamics was proposed in[22].With the development of intelligent control methods,in recent years,by combining intelligent control with inverse systems,the inverse decoupling control methods were proposed in[23]-[27].

The above methods are designed without considering the performance requirements on the systems.Although they can realize decoupling control of complex industrial processes,they cannot meet the rising performance index.Therefore,if the above decoupling control methods are used,the integrated optimization control of complex industrial processes aimed at saving energy and reducing consumption will be influenced.With the rapid development of science and technology,the performance requirements on many control systems(such as spacecraft,modern industrial equipment,and production process,etc.)become higher and higher.For a control system,it is always hoped that a certain performance index is optimal in some sense.Optimal control is a subject that studies and solves the optimal solution among all possible control schemes,which provides a feasible scheme to realize the optimal performance of a control system.

This paper proposes an optimal decoupling control method for a class of continuous time linear multivariable systems,by combining open-loop feedforward decoupling control with optimal tracking control.First,by introducing one virtual input vector,the differential equation on state is converted into the differential equation on output,and then the system matrix and input matrix are decomposed into a diagonal matrix and the matrix with zero diagonal elements,such that the coupling terms are separated.Second,by introducing the other virtual input vector,the system is open-loop decoupled by using feedforward and output feedback method.Finally,for the decoupled system,the conventional optimal tracking control method is adopted to realize the tracking of the system to any reference input.By choosing appropriate weighting matrices,the optimal decoupling control method is equivalent to the closed-loop optimal decoupling control method.Simulation results show the effectiveness of the proposed method and the superiority as compared with conventional optimal quadratic tracking(LQT)control method.

II.PROBLEMDESCRIPTIONS

Consider a continuous-time linear multivariable timeinvariant system

where x(t)∈Rnis the system state,u(t)∈Rmis the control input,y(t)∈ Rmis the system output;A ∈ Rn×n,B ∈Rn×m,C ∈Rm×nare constant matrices with CB invertable,{A,B}controllable,{A,C}andobservable,where Q is defined in the sequel.

The conventional optimal tracking control problem is tofind the optimal control policy u∗(t)so as to make the system(1)track a desired reference trajectory yr(t)∈Rnin an optimal manner by minimizing a predefined performance index,especially,

where e(t)=yr(t)-y(t)is the tracking error,Q=QT≥0 is a nonnegative matrix,and R=RT≥0 is a positive matrix.The standard optimal tracking controller is given as[28]

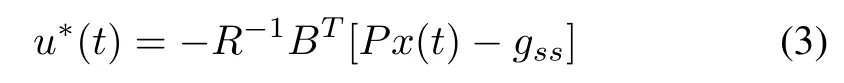
where P is obtained by solving the Riccati equation

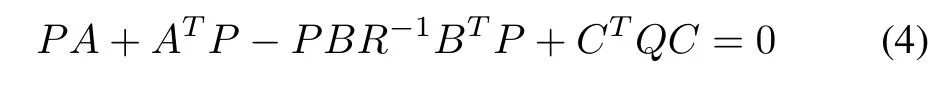
and the limiting function gssis given by gss=limT→∞g,with the auxiliary time signal g satisfying

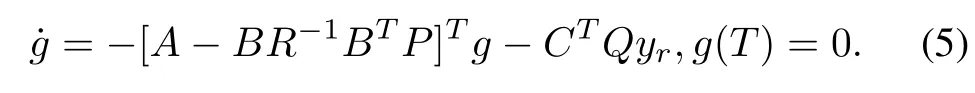
The optimal output trajectories can be then obtained by computing

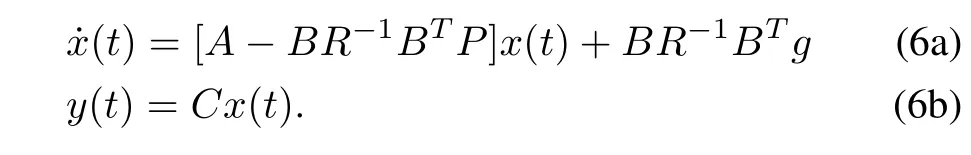
From(5)and(6),the transfer function matrix from yr(t)to y(t)may be non-diagonal,and the change of one reference input yr,i(t),i=1,...,m must lead to the changes of other outputs yj(t),i/=j.In fact,many industrial processes have the coupling characteristics.For industrial processes with weak coupling,distributed control and model predictive control are generally used.However,if an industrial process is strongly coupled,an effective decoupling control method is necessary.

The purpose of this paper is to derive an optimal decoupling control law,so that the system output y(t)of the closedloop system can track the reference input yr(t)as much as possible,and the influence of the couples among control loops is suppressed to be as small as possible,while the closed-loop system achieves a certain optimal performance.

III.OPTIMALDECOUPLINGCONTROL

A.Differential Equation on Output

To realize input-output decoupling control,we should first convert the differential equation on state into the equation on output.

From(1),we know

Define

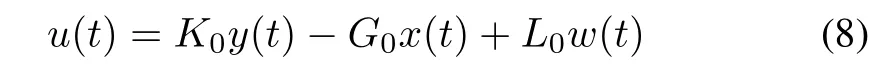
where K0∈ Rm×m,G0∈ Rm×n,L0∈ Rm×mare constant matrices,and w(t)∈Rmis the first virtual input vector.By substituting(8)into(7),we have

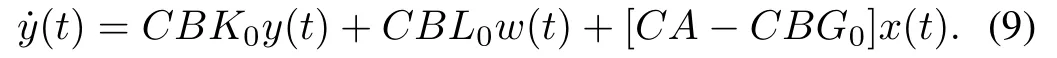
Select

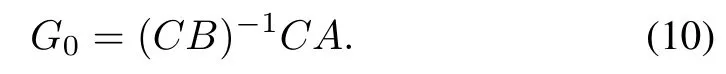
(9)can then be converted into the following equation:

Equation(11)can be viewed as a generalized system.In the sequel,it will be considered directly,and an optimal decoupling control w∗(t)will be designed.

B.Decoupling Control Scheme

Since the coupling effect of the ith channel’s input wi(t)on the jth channel’s output yj(t),i/=j can be regarded as measurable disturbance,in the design,it will be eliminated by a feedforward method.The effect of the ith output variable on the jth output variable in the autonomous system w(t)=0 will be eliminated by applying a feedback method.Therefore,we rewrite(11)as

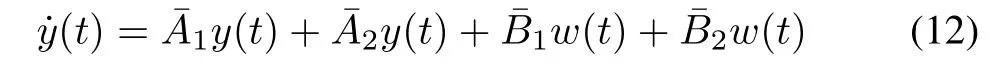
By introducing the second virtual input vector v(t)∈Rm,we design the following decoupling controller:

where S1,L are diagonal matrices with corresponding dimensions where S1is invertible,and S2,K are matrices whose diagonal elements are zeros.By left-multiplying(12)using S1and left-multiplying(13)usingwe have

From(14),to achieve decoupling,S1,S2,K should be chosen to satisfy the following equations:

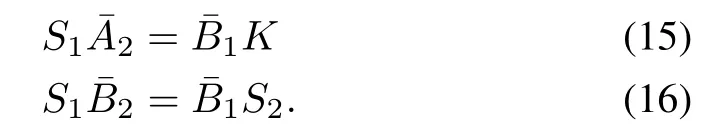
Then,(11)is converted to

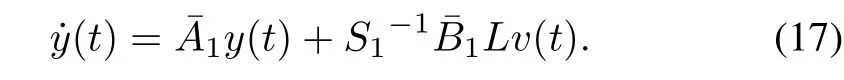
C.Optimal Tracking Control

In the following,for(17),we will design the virtual input v(t)by using the conventional optimal tracking control method.The performance index is

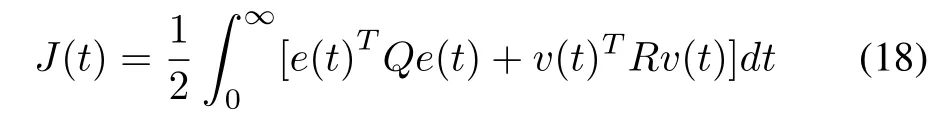
where e(t)=yr(t)-y(t)is the tracking error,Q=QT≥0 is a nonnegative matrix,and R=RT≥0 is a positive matrix.

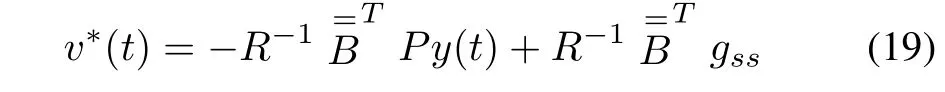
where P is the symmetric positive definite constant matrix which satisfies the following Riccati algebraic equation:

and gssis given by gss=limT→∞g with the auxiliary time signal g satisfying

Then,from(13)and(19),the optimal decoupling control law is finally obtained as follows:

The structure of the optimal decoupling control system is shown in Fig.1.

where the symmetric positive definite constant matrix P satisfies the following Riccati algebraic equation:

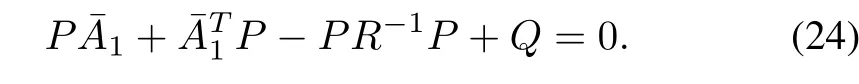
and gssis given by gss=limT→∞g with the auxiliary time signal g satisfying

Fig.1.Structure of the optimal decoupling control system.

D.Performance of the Optimal Decoupling Controller

The optimal decoupling controller(23)is realized by first decoupling the generalized system(11)and then designing the optimal tracking controller.Therefore,it is actually an openloop decoupling controller.In the following,we will show that the open-loop decoupling controller equals a closed-loop optimal decoupling controller in a sense.

Theorem 1:For the generalized system(11),the optimal decoupling controller(23),with P satisfying(24)and g(t)satisfying(25),makes the following performance index minimized.

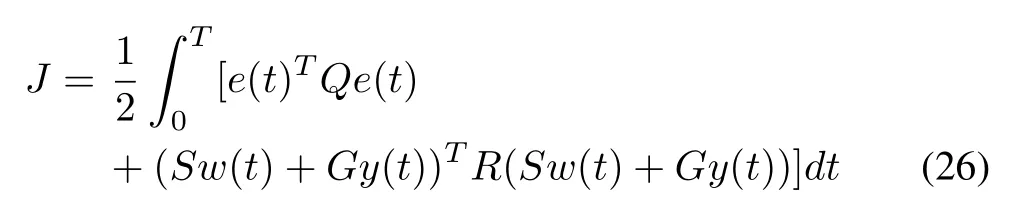
Proof:The optimal control minimizing the performance index(26)must satisfy the minimum principle;thus,the Hamiltonian function is introduced.

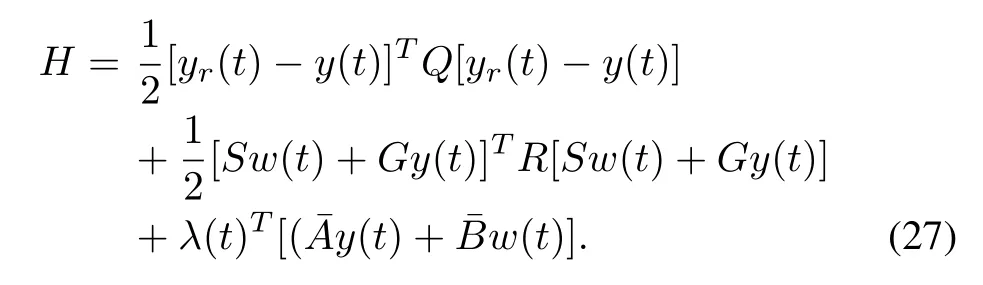
From the extreme value condition

the optimal control is obtained as

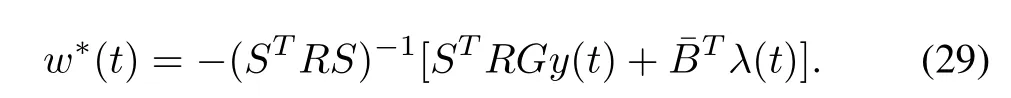
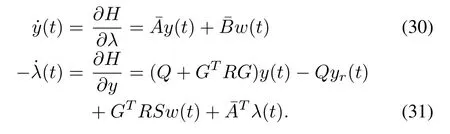
Let

then,we have

From(31),we know

By comparing(34)and(35),and making them to hold for any y(t)and yr(t),the matrix P and g(t)must satisfy the following equations:

Substituting(32)into(29),the optimal control can be obtained as

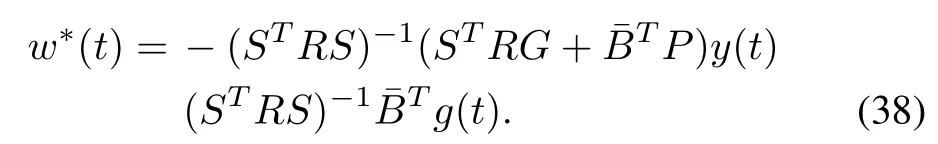
Remark 1:Since the optimal decoupling controller(23)minimizing the performance index(26)is derived by using one step,it is also a closed-loop decoupling scheme.

IV.SIMULATIONS

To illustrate the effectiveness of the proposed method,in this section,we will apply it to a ball mill coal-pulverizing system.

As described in[21],ball mill coal-pulverizing systems are important heat-power equipment in power plants.They are used to pulverize raw coal into fine powder of desired temperature and fineness.There are plenty of coal mines in China,but the quality of raw coals varies greatly.Therefore,ball mill coal-pulverizing systems are widely used to grind various raw coal.The flowchart of ball mill coal-pulverizing system is shown in Fig.2,which consists of a hopper,a feeder,a strap transmission system,a ball mill,a coarse powder separator,a fine powder separator and a blast system[21].The raw coal is leaked from the hopper to the feeder,sent into the dryness pipeline by the strap transmission system,and then blended with dryer air.The quantity of dryer air and heat can be regulated by the flow rates of hot air and warm air in the blast system.The mixture of raw coal and dryer air are sent into the ball mill through the dryness pipeline,where it is pulverized to fine powder by knocking and grinding of iron balls when the ball mill rotates.At the same time,the coal powder is dried and brought out of the ball mill by dryer air.Then,it is transferred into the coarse separator,where the coarse powder and fine powder are separated.The unqualified coarse powder is returned into the ball mill for re-grinding,while qualified fine powder is sent into the bunker and then to boiler for burning.

Fig.2.Flowchart of the ball mill coal-pulverizing system.

According to the energy and mass equilibriums of ball mill entrances and the mass equilibrium of liquid in the blast pipes,a dynamic model of the ball mill coal-pulverizing system is established as follows[21]:

where x1=y1is the outlet temperature of the ball mill,which is related to the grinding quality of the coal-pulverizing system;x2=y2is the inlet pressure of the ball mill,which is related to system security;x3=y3is the import and export differential pressure of ball mill,which is connected with the production of ball mill;u1,u2,and u3are respectively the coal feeding rate,the hot air flow and the warm air flow.The meanings and values of other variables and parameters can be found in[29],and they are respectively listed in Table I and Table II.

From(42),the ball mill coal-pulverizing system is a nonlinear process with strong couplings between each loop.Variations of each control input will cause the changes of all the system outputs.According to the observation on site,the strong coupling property is mainly reflected in following cases:

1)When the coal feeding rate,u1,increases,more heat of the desiccant will be absorbed into the ball mill.Therefore the outlet temperature of the ball mill,y1,will decrease.Simultaneously,the increase of the coal feeding rate,u1,can also increase the ventilation friction inside of the ball mill,resulting in a decrease in ventilation volume.Consequently,the inlet pressure of the ball mill,y2,decreases.The increase of the coal feeding rate,u1,also makes the mill load inside the ball mill increase,and then leads to the increasing of the differential pressure of the ball mill,y3.

2)When the hot air flow,u2,increases,the corresponding hot air volume will increase.Then,the outlet temperature of the ball mill,y1,will increase and the inlet pressure and the differential pressure of the ball mill,y2and y3,will decrease.

3)When the warm air flow,u3,increases,the corresponding warm air volume will increase.Then,the outlet temperature and the inlet pressure of the ball mill,y1and y2,decrease,and the differential pressure of the ball mill,y3,increases.

Therefore,it is very important to decouple the control of the ball mill coal-pulverizing system.

TABLE I DEFINITIONS OFPARAMETERS ANDVARIABLES IN COAL-PULVERIZINGSYSTEMMODEL

TABLE II DATA OFPARAMETERS ANDVARIABLES INCOAL-PULVERIZING SYSTEMMODEL

According to the requirements of the practical process,the outputs y1(t),y2(t)and y3(t)should be controlled respectively between 60◦C-85◦C,-0.2kpa--0.6kpa and 0.5kpa-2.0kpa[29].In the simulations,we choose(y1,y2,y3)=(78◦C,-0.4kpa,1.2kpa)and(82◦C,-0.5kpa,1.7kpa),which lie in the ranges of the outputs,as the equilibrium/operational points.First,the initial values,i.e.,the raw coal temperature tc=15,the warm air temperature tlk=30,and the hot air temperature tr=340 are selected.Then,we linearize(42)respectively at the above two equilibrium/operational points.

For(y1,y2,y3)=(78◦C,-0.4kpa,1.2kpa),we have

The relative gain matrix is as follows:

From the RGA matrix,we know that it is reasonable to select the coal feeding rate u1(t)to control the outlet temperature of the ball mill,y1(t),the hot air flow u2(t)to control the inlet pressure of the ball mill,y2(t)and the warm air flow u3(t)to control the differential pressure of the ball mill,y3(t).Since the relative gains of the three channels are 0.6417,2.0054 and 2.6433,respectively,according to the Bristol-Shinskey metrics,there exists serious coupling in the loops.Select the weighting matrices as

and the reference input as

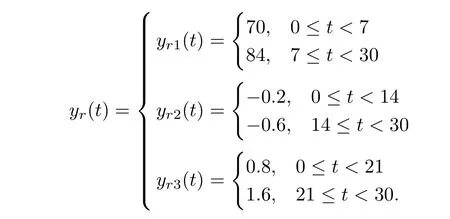
Fig.3 is the output tracking curves by using the proposed optimal decoupling control method,and Fig.4 is the corresponding control input curves.From Fig.3,the three output variables can all track their reference curves well.In order to compare with the proposed method,the conventional LQT control method is also used.Fig.5 is the corresponding output tracking curves,and Fig.6 is the control input curves.From Fig.5,we can see that due to the existence of the couplings,the output y1cannot track its reference input at all.

For(y1,y2,y3)=(82◦C,-0.5kpa,1.7kpa),we have

The relative gain matrix is as follows:

Fig.3.Tracking results by using the proposed controller.

Fig.4.Input signals by using the proposed controller.

Fig.5.Tracking results by using the LQT controller.

Fig.6.Input signals by using the LQT controller.

From the RGA matrix,we know that there still exists serious coupling in the loops.Select the same weighting matrices as in the above example and the reference input as below

Fig.7 is the output tracking curves by using the proposed control method,Fig.8 is the corresponding control input curves,Fig.9 is the output tracking curves by using the conventional LQT control method,and Fig.10 is the corresponding control input curves.From Figs.7 and 9,we can see that the tracking effect produced by using the proposed method is better than that produced by the LQT method.

Fig.7.Tracking results by using the proposed controller.

Fig.8.Input signals by using the proposed controller.

To verify the effectiveness of the proposed method for the ball mill coal-pulverizing system,in the following,we will conduct simulations on the ball mill coal-pulverizing system(42)around a small neighbourhood of the point(y1,y2,y3)=(82◦C,-0.5kpa,1.7kpa).

The weighting matrices are selected as in the above two examples,and the reference input is as

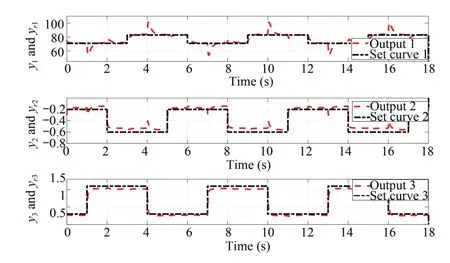
Fig.9.Tracking results by using the LQT controller.

Fig.10.Input signals by using the LQT controller.

Since the nonlinearity is weak around the small neighbourhood of the equilibrium/operational point,the linear decoupling control method can be used to control the nonlinear system.Fig.11 shows the output tracking curves by using the proposed optimal decoupling control method,from which we can see the three output variables can all track their reference curves well.In order to compare with the proposed method,the nonlinear decoupling control method[21]is also used.The sampling time T=0.01 is selected.The parameters of the controller are chosen same as that in[21].Fig.12 is the output tracking curves.From Figs.11 and 12,we can see that the effect produced by the proposed method is not worse than that produced by the nonlinear decoupling control method.

V.CONCLUSIONS

In this paper,for a class of linear multivariable systems with strong couplings,an optimal decoupling control method is proposed by combining an open-loop decoupling compensator and an optimal tracking controller.From the design method point of view,this method belongs to the open-loop decoupling domain.However,it is also proved to be equivalent to the closed-loop decoupling control in a sense.Therefore,the method can not only eliminate the coupling effects in the loops,but also can improve the closed-loop performance index,and can realize the tracking of any reference input of the system.Two linear models are obtained by linearizing a ball mill coal-pulverizing system at two equilibium/operational points.Simulations are conducted respectively for the two models.The results show the effectiveness and superiority of the proposed method as compared with the conventional LQT control method.Simulations are also conducted on the ball mill coal-pulverizing system.The results show that around a small neighbourhood of the equilibium/operational point,the effect produced by the proposed linear decoupling control method is not worse than that produced by the nonlinear decoupling control method[21].

Fig.11. Tracking results by using the optimal decoupling control in the ball mill.

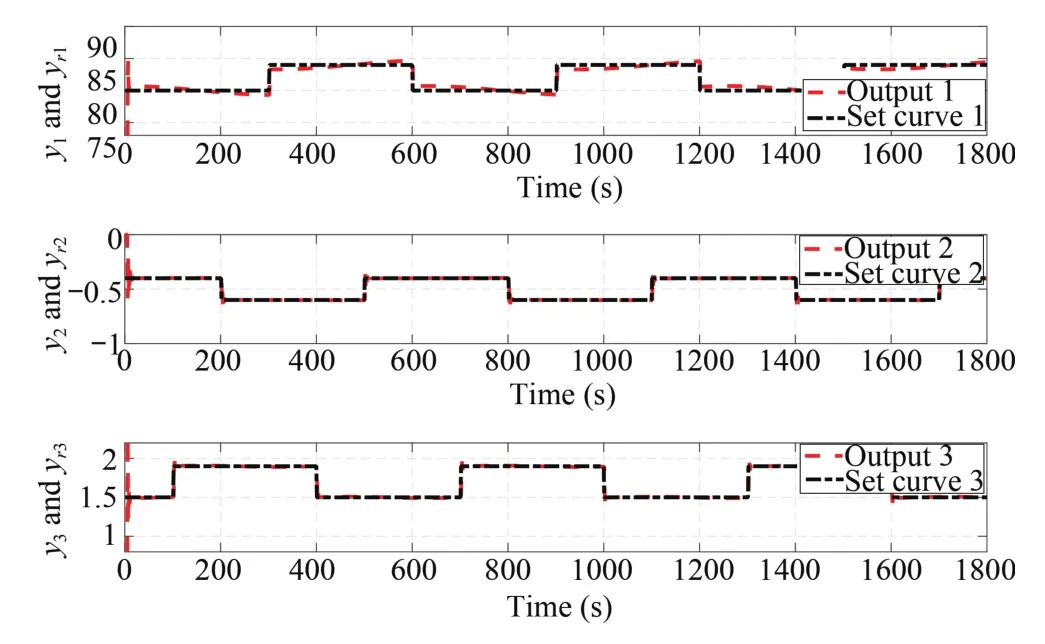
Fig.12. Tracking results by using the nonlinear decoupling control[21]in the ball mill.

The proposed optimal decoupling control method is designed for linear systems with completely known dynamics.Although it is also effective for nonlinear systems with weak nonlinearity,it cannot be directly applied to a nonlinear system with strong nonlinearity.In the future,we will study adaptive optimal decoupling control methods for nonlinear systems with strong nonlinearity and unknown dynamics.