基于化学发光免疫分析仪三轴取样模型的交叉耦合控制

薛 鹏，杨力滔

（长春工业大学 电气与电子工程学院，吉林 长春 130022）

基于化学发光免疫分析仪三轴取样模型的交叉耦合控制

薛 鹏，杨力滔

（长春工业大学 电气与电子工程学院，吉林 长春 130022）

化学发光免疫分析仪是临床医学免疫检测中必不可少的医疗设备。在三轴取样平台中，需要取样针快速、精准地在试剂样品区、试剂反应区和清洗区运动。为了提高其精度，简要介绍了三轴取样平台的数学模型，阐述了造成取样针偏差的轮廓误差计算模型，提出了基于交叉耦合控制方法的变增益交叉耦合控制方法，最后在Matlab/Simulink环境下搭建双轴变增益交叉耦合控制系统仿真模型，并对其进行必要的分析。

三轴取样；两轴控制系统；轮廓误差；交叉耦合

化学发光免疫分析仪是临床医学检测技术的一种，其取样部分通常采用三轴运动平台取样控制系统，取样控制对取样针运动的速度和精度有较高的要求。为了提高其取样控制的精度，建立三轴运动控制系统，XY轴负责定位控制，Z轴负责垂直运动，以便取样针能够准确完成取样工作。鉴于此，取样平台控制精度的重点是要提高两轴控制系统的协调性[1]。采用交叉耦合的控制方法来提高两轴运动的协调性得到了越来越多人的认可，通过每个轴的跟踪误差来反映轮廓误差，运用交叉耦合的方式计算出每个轴的补偿量，将结果补偿到各轴上，以此消除该轴对其他轴所造成的影响[2]。本文采用变增益交叉耦合的算法研究两轴运动，而仿真验证表明轮廓精度有所提高。

1 三轴运动平台的系统模型

取样平台的三轴运动控制系统采用两两垂直的永磁同步直线电机进行轮廓误差实验，该电机具有推力大、损耗小、响应快等特点。永磁直线同步电机运动方程式可以表示为[3]：

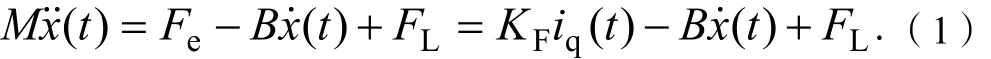
式（1）中：M为动子和动子负载的总质量；Fe为电磁推力；（t）为动子位移；B为黏滞摩擦系数；KF为推力系数；FL为外部扰动；iq为动子q轴电流。

令（t）和动子速度v（t）为状态变量，永磁直线同步电机的状态方程可以表示为：

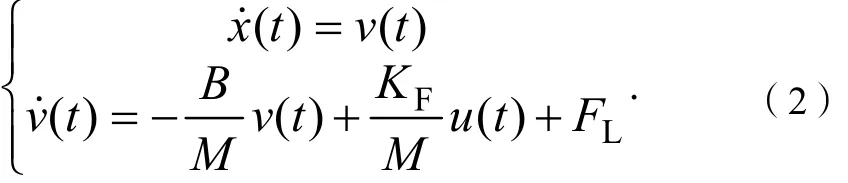
式（2）中：u为控制输入，u＝iq。

那么，三轴运动平台的状态方程为：

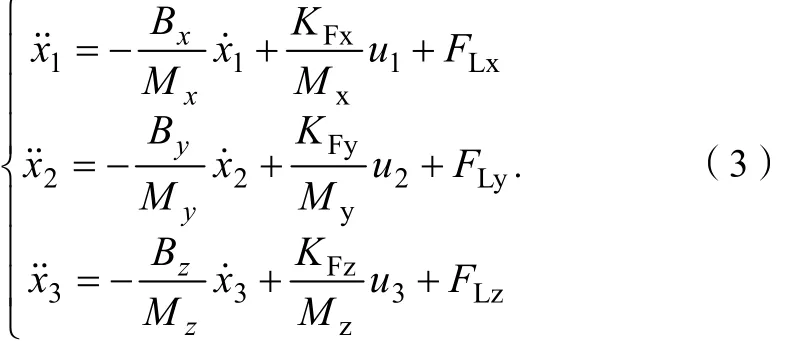
式（3）中：x1、x2、x3分别为x轴、y轴、z轴的位置输出；u1、u2、u3为q轴定子电流的输入，其中，u1＝iq1，u2＝iq2，u3＝iq3。

2 轮廓误差定义

XY轴平面上的轨迹误差分为跟踪误差和轮廓误差。跟踪误差，是指某一时刻实际位置与预期位置的偏差值；轮廓误差，是指瞬时点的实际位置距离轨迹法线上的偏差值。轮廓误差是在双轴运动过程中产生的，主要影响因素是每个轴的跟踪误差。图1为取样平台运动过程中产生的误差示意图，其中，R为某时刻的指定运动位置，A为该对应时刻的实际运动位置，θ为指定运动位置的轨迹切线与X轴的夹角，e为运动平台的跟踪误差，ε为运动平台的轮廓误差，ex、ey为双轴XY的跟踪误差分量，εx、εy为双轴XY的轮廓误差分量。

对于曲线轮廓，一般采用圆来近似逼近轮廓曲线，曲线上某时刻的指定位置处的曲率半径ρ代替圆的半径，则有：

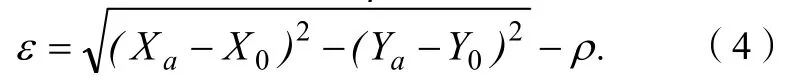
式（4）中：Xa、Ya为实际的运动位置点坐标；X0、Y0为该时刻运动点处弧线对应的曲率中心坐标。

至此，则有：

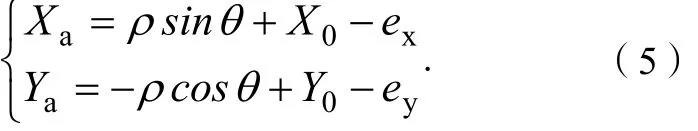
将式（5）代入式（4）中可得：

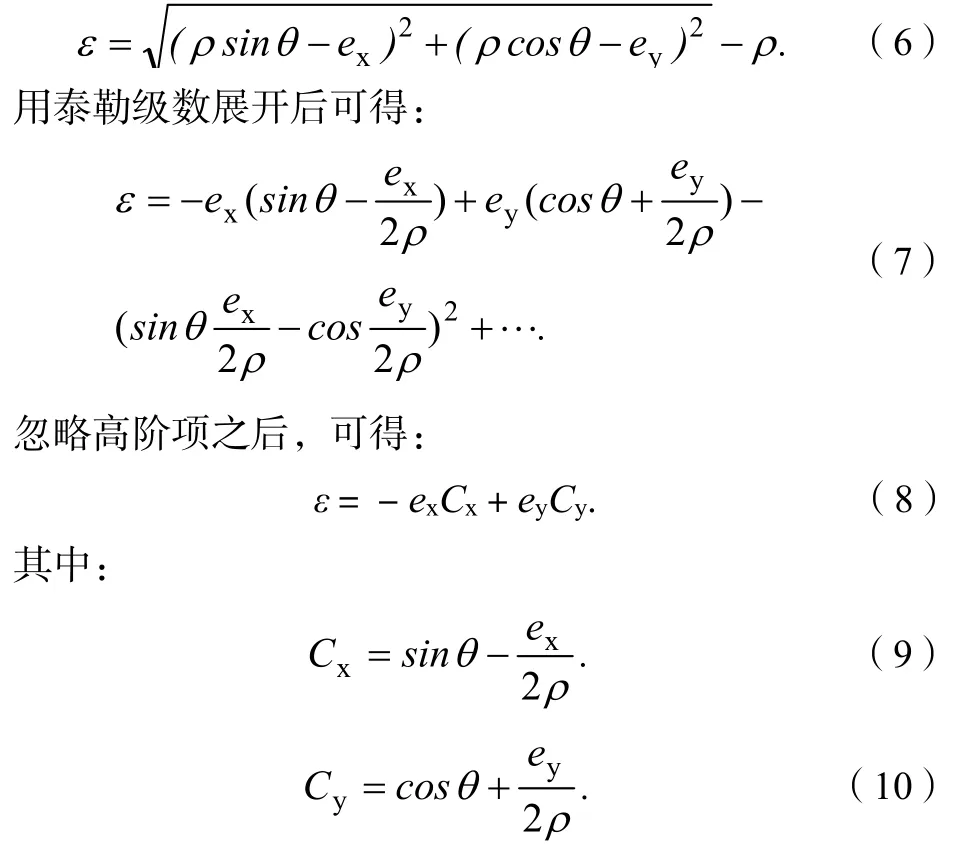
式（8）（9）（10）中：Cx、Cy为交叉耦合增益系数。

因此，由式（8）可以看出，交叉耦合增益随着取样运动的进行随时发生变化，所以，系统的轮廓误差一般为取样运动轨迹轮廓误差的表达式，是变增益的。

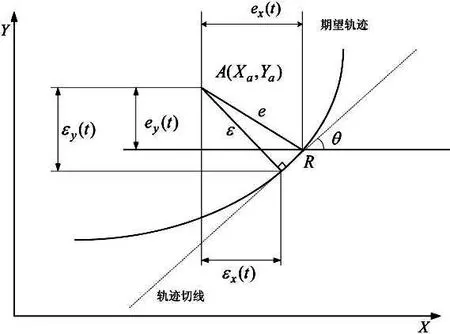
图1 跟踪误差与轮廓误差模型

3 交叉耦合控制系统的方法

取样平台运动过程中产生的误差主要来源于单轴的跟踪误差和多轴之间的轮廓误差。双轴联动对取样针进行定位时，要求双轴动态配合好，减小位置轮廓误差。因此，提出通过减少轮廓误差提高取样针定位精度的交叉耦合轮廓控制概念[4]。由式（8）（9）（10）可知，轮廓误差是由各轴的跟踪误差造成的，从控制的角度来讲，是将轮廓误差的开环控制变为闭环控制[5]。

变增益交叉耦合的控制方法实际上就是根据多轴的反馈信息，对轮廓误差模型实时的进行修正，寻求最佳补偿反馈到各轴，以此来减小轮廓误差[6]。根据式（8）（9）（10）设计变增益交叉耦合控制方法，如图2所示。对于同一轮廓的不同位置，其交叉耦合增益系数也是不同的。

图2中，rx、ry和ex、ey分别为XY轴的参考输入和跟踪误差；Cx和Cy分别为XY轴的交叉耦合增益系数；Cc为变增益交叉耦合控制器。ex、ey作为交叉耦合控制器的输入，其输出量通过Cx和Cy分解至两轴上，以此达到协调控制。交叉耦合控制器采用PID控制方法，这种控制方法实时性良好，不需要实时调节输入参数，在控制框架不变的情况下可以很好地降低轮廓误差。交叉耦合控制器参数随取样针运动轨迹位置的改变而改变。

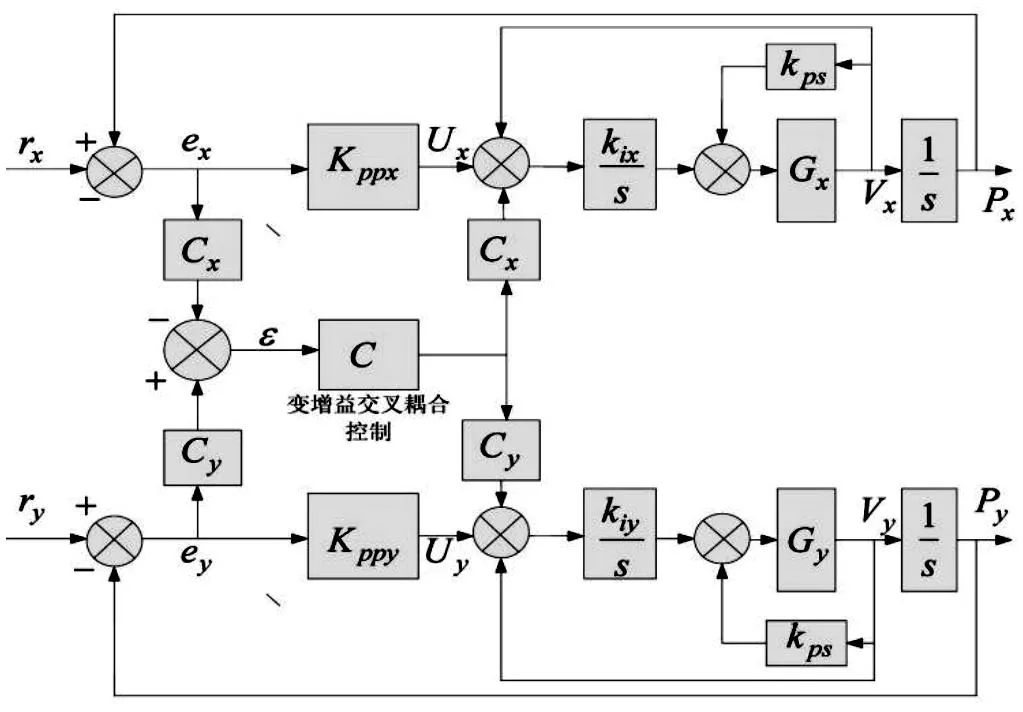
图2 双轴变增益交叉耦合控制系统框图

4 取样平台双轴交叉耦合控制系统建模与仿真

为了验证变增益交叉耦合控制方法对控制系统降低误差的效果，针对取样平台双轴控制系统，利用Matlab软件对轮廓控制进行仿真。XY采用相同的永磁直线同步电机，其参数为：J＝15 kg，B＝0.2 N·s/m，Kf＝15 N/A。

跟踪曲线为半径1 mm的圆，即L＝｛（x（t），y（t））∈R2：x（t）＝sint，y（t）＝cost，t∈[0，2π]｝.利用具有变增益交叉耦合控制和无交叉耦合控制2种方法分别进行仿真，可以直观地进行比较。变增益交叉耦合参数设为：Kpp＝15，Ki＝150，Kp＝40，Kci＝25，Kcp＝0.2，Kcd＝0.1；无交叉耦合控制参数为：Kpp＝15，Ki＝150，Kp＝40.仿真结果如图3、图4所示。

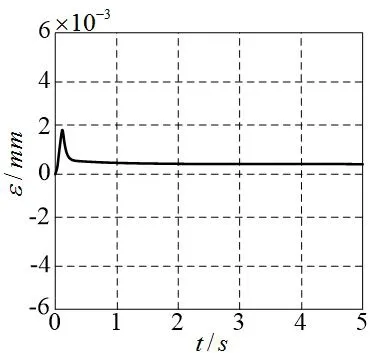
图3 变增益交叉耦合控制轨迹轮廓误差

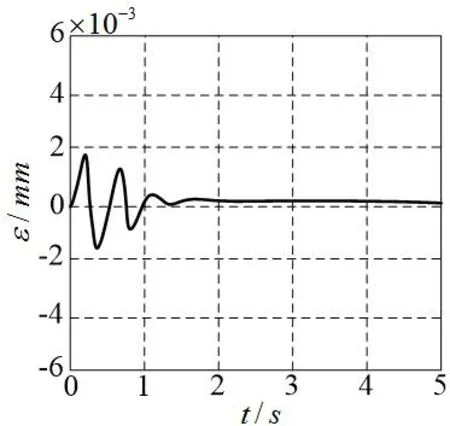
图4 无交叉耦合控制轨迹轮廓误差

由图3、图4可知，采用无交叉耦合的控制方法震荡比较大，误差稳定时间长。而变增益交叉耦合的控制方法能够在较短的时间内达到稳定状态，双轴变增益交叉耦合的控制方法减小了双轴协调运动引起的轮廓误差，能够更好地保证取样平台的精度，减小跟踪误差和轮廓误差。

5 结论

化学发光免疫分析仪的核心之一是运动控制部分。对于三轴取样控制平台，要想提高取样精度，采用变增益交叉耦合的控制算法是有效的，并且在数控机床系统中也有良好的应用发展。本文利用变增益交叉耦合控制器，即时补偿耦合误差，减小轮廓误差，使PMLSM驱动的双轴取样平台能够更加精准地控制位置。

［1］孙宜标，宋杨，郭庆鼎.XY平台直线伺服系统的IP变增益交叉耦合控制［J］.组合机床与自动化加工技术，2007（11）：40-43.

［2］Koren Y.，C.C.Lo.Variable gain cross-coupled controller for contouring［J］.Annals of the CIRP，1991，40（1）：371-374.

［3］夏加宽，张琳娜，孙宜标，等.直线电机XY平台交叉耦合迭代学习控制［J］.沈阳工业大学学报，2013，35（1）：1-5.

［4］Syh-aShiuh Yehk，Pua-Lo Hsu.A New Approach to Biaxial Cross-coupled Control［C］//Proceeding of the 2000 IEEE International Conference on Control Applications.Anchorage，Alaska，USA，2000：168-173.

［5］李圣宜，张云洲，张明亮，等.超精密机床的变增益交叉耦合控制研究［J］.基础自动化，2000，7（2）：25-28.

［6］张建国.基于滑模变结构控制的多轴协调运动控制策略研究［D］.济南：山东大学，2007.

TM921.541

A

10.15913/j.cnki.kjycx.2018.01.114

2095－6835（2018）01－0114－03

〔编辑：白洁〕