基于自步学习多元回归分析
2018-12-22甘江璋赵树之
甘江璋,钟 智,余 浩,雷 聪,赵树之
(1.广西师范大学 广西多源信息挖掘与安全重点实验室,广西 桂林 541004;2.广西师范学院 计算机与信息工程学院,广西 南宁 530023)
0 引 言
多元回归问题在现实应用中普遍存在,而且常用高维特征数据进行描述,但离群样本和高维属性都会影响多元回归分析的准确度和效率[1-3]。所以,如何处理离群样本和高维数据对于建立有效可靠多元回归模型具有重要的研究价值。
现有处理高维数据的方法有子空间学习[4]和属性选择两种[5]。属性选择方法既可以保持数据的原有功能,又提高了算法的效率[6]。而处理离群样本的方法主要有基于距离方法[7]和基于聚类的方法[8]等,基于聚类的方法主要通过将远离类簇的少数样本判定为离群样本。基于距离的方法将与数据集中大部分样本距离大于阈值的样本判为离群样本,从而达到处理离群样本的目的。
然而,现有的回归分析算法只是单一考虑其中一种因素的影响(离群样本或高维大数据),因此在本文提出了一种基于自步学习多元回归分析算法(multiple regression analysis based on self-paced learning,SPM_RS)来同时处理高维大数据和离群样本,以此来获得更好的效果。具体地,首先利用自步学习方法对数据中的训练样本进行选择,有效避免离群样本带来的影响,然后引入稀疏学习理论,使用可以导致行稀疏的2,1范数进行属性选择。经实验验证,结合了自步学习和稀疏属性选择的多元回归分析方法在应用中各项评价指标均优于对比算法。
1 相关理论背景
1.1 多元分析
多元回归分析是研究多个变量之间相关关系的一种重要统计分析方法,因其坚实的内在理论基础被广泛应用于自然科学,社会科学和应用技术中等领域[9]。
假设样本xi由d个属性来描述,回归分析的本质就是试图学到一个模型尽可能的预测出样本标签yi,使用最小二乘法对样本标签yi进行线性回归拟合,这样可以得到模型
f(xi)=xiW+b
(1)
其中,W表示回归模型参数,b表示模型偏差项。
在实际任务中,为了使模型尽可能更好拟合原始数据,需要模型的拟合误差尽可能的小。但是在多元回归问题中,高维大数据普遍存在,会使回归模型出现过拟合的问题。为了缓解模型的过拟合,常在多元回归模型中引入稀疏学习理论[10]。
在稀疏学习的基本理论中,通过稀疏正则化项对回归模型参数W进行稀疏假设,并使用训练数据对W进行拟合,则可以得到模型

(2)
其中,φ(W)为稀疏正则化项,α表示调节参数用来平衡拟合损失函数项和稀疏正则化项,n为样本数。
在稀疏学习中,正则化项通常选择能够凸优化求解的范数[14]。其中1范数具有较强的稀疏性,2范数具有防止损失函数过度拟合。而2,1范数融合了两者之间优点,既有1范数稀疏性的特点又有2范数防止过度拟合的特点。因此本文采用2,1范数作为稀疏正则化项进行对W行稀疏处理,排除冗余信息和不相关的属性,从而提升算法效率。
1.2 自步学习简介
自步学习[11]是一种模拟人的认知机理的机器学习方法,人类对事物的认识都是从简单的知识过度到复杂知识。我们在机器学习的模型中引入这一机制,利用自步学习的方法首先学习简单样本再逐步将复杂的样本纳入训练当中。
给定一个数据集E(xi,yi)有n个样本,xi表示一个样本,yi表示与该样本对应的类标签,W表示模型需要优化的参数,r(W)为参数的正则化项。用损失函数L(xi,yi,W)来表示样本的“难易”程度,则可以得到传统的机器学习目标函数
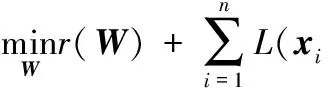
(3)
自步学习的核心思想在于每一次的迭代都倾向于选择“简单”的样本来更新模型参数[12]。每次迭代选择的样本数量由自步学习参数来确定,通过逐次增加自步学习参数将更多的训练样本纳入训练当中。因此,自步学习在传统的机器学习目标函数中引入一个变量v用以表征样本是否被选择的程度,则自步学习的目标函数为

(4)
其中,f(v,λ)为自步正则化项,λ为自步正则化参数,用于控制哪些样本被选择,如果λ的值较小,目标函数的优化过程就倾向于选择L(·)较小的样本。随着迭代次数的增加,逐步增大λ的值,将更多的样本纳入训练。
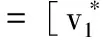
这种迭代优化的策略在当使用固定的W更新v的时候,将损失小于阈值λ的样本作为“简单”样本,并选择这些“简单”样本进行训练。当用固定的v来更新W的时候,只对所选择的“简单”样本进行训练,得到模型参数W。其中λ也相当于模型的“年龄参数”,随着λ值的增加,那些“复杂”的样本也会被选择,这样模型也会变得更加成熟,泛化能力更强。
2 算法描述和优化
2.1 算法描述
给定一个训练数据集X=[x1,x2,…,xn]∈Rn×d,n表示样本数量,d表示属性维度。Y∈Rn×c表示样本类标签,c表示样本对应的类数。使用最小二乘法来拟合模型参数和数据,得到如下模型
(5)

大部分数据中普遍存在不相关信息和离群值,会对实验结果造成一定影响。所以,找到一个合适的规则化项对于提高算法性能有很大的作用。2,1范数既有良好的行稀疏性,又能防止模型的过拟合,对于去除一些冗余信息有很好的效果。本文采用2,1范数对重构系数矩阵进行稀疏,得到的模型为

(6)
其中,α为稀疏正则化参数,α越大则矩阵越稀疏。
在传统的机器学习模型训练过程中通常会将所有样本一次加入到训练中,这样的学习方式没有充分考虑到噪声给模型训练带来的影响,因此在本文中采用自步学习的方法有意义的对样本进行选择,这样得到的目标函数如下所示

(7)
SPM_RS算法的伪代码如下:
算法1: SPM_RS算法伪代码
输入: 训练样本X∈Rn×d,Y∈Rn×c控制参数α,λ。
输出: aCC
(1)初始化t=1。
(2)初始化矩阵D∈Rd×d,v∈R1×n。
(3)通过式(13)求解W。
(4)根据得到的W,更新Dt,计算λ。
(5)根据λ值,更新v。
(6)t=t+1,重复步骤(3)~(6)。
(7)直到式 (8) 收敛。
(8)最后,对新的属性集构成的样本使用SVR进行回归分析。
2.2 算法优化
本节对文中提出的目标函数进行优化

(8)
目标函数存在两个变量,所以本文采用交替优化方法。
定义一个对角矩阵D
(9)
(1)固定v,优化W:固定v后,目标函数变为

(10)
为方便优化将式(10)写成如下所示
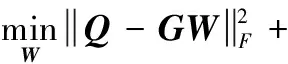
(11)
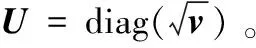
对式(11)中W求导可得

(12)
最终求出的结果为
W=(GTG+αD)-1GTQ
(13)
(2)固定W,优化v问题变成

(14)


(15)
对式(15)求导可得最优解
(16)
2.3 算法收敛性证明
根据算法2可得第t次迭代的W(t+1)

(17)
由式(17)可得

(18)
将对角矩阵D代入式(18)可得

(19)
对于W(t)和W(t+1)的每一行,可以得到下列不等式

(20)
对上述不等式乘以控制参数α,并累加得到
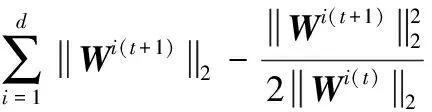
(21)
最后,结合不等式(18)和式(20)就可以得到
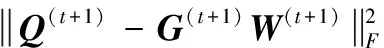
(22)
根据上述不等式可以得出,目标函数的值在迭代的过程中是单调递减的,所以SPM_RS算法可以收敛到当前选择样本下的最优解。
3 实验结果和分析
3.1 实验数据集和对比算法
本文使用6个数据集来测试算法在回归分析上的性能。数据集来源于UCI[16],信息统计见表1。
本文通过与4种优秀对比算法的实验结果比较来评估提出的算法:LSG21[17]方法,CSFS[18],SLRR[6]和RSR[19]方法。在实验中使用平均相关系数(average correlation coefficient,aCC)来评估回归的准确性。

表1 数据集信息统计
3.2 实验结果和分析
实验中的对比算法和SPM_RS算法均采用十折交叉验证来对比算法性能,在每一折中再进行5折交叉验证,并且使用SVR学习训练得到回归模型。
SPM_RS算法与对比算法在6个数据集上每一折的aCC对比如图1~图6所示。由于十折交叉验证的随机性,所以SPM_RS算法并不是在每一折上都是最好的,但是10次实验结果大部分都高于对比算法,最后的平均aCC也优于对比算法。
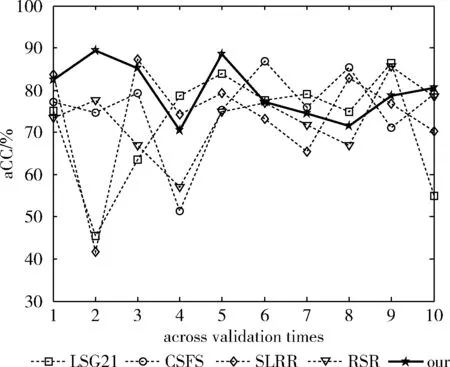
图1 数据集EDM

图2 数据集ATP1d

图3 数据集ATP7d

图4 数据集OES10

图5 数据集sf1

图6 数据集OES97
在表2中的数据可以看出,SPM_RS算法的平均aCC在6个数据集上与另外的4种对比算法的平均aCC进行了比较。在6个数据集上SPM_RS算法获得了最高的aCC。具体的,在EDM数据集上SPM_RS算法取得了最好的79.83%,比LSG21高出了7.85%,比CSFS,SLRR,RSR分别高出4.2%6.38%,6.88%。在数据集ATP7d上SPM_RS算法的aCC是87.13%,相对于其它对比算法分别高出8.29%,10.13%,7.22%,11.39%。在sf1数据集上SPM_RS算法比对算法提高了5.92%,4.9%,13.38%,3.61%。其中在OES97上提高的最多,高出了13.38%。在所有的数据集中,SPM_RS算法也比对比算法高出7.21%,7.11%,5.79%,5.88%。可见SPM_RS算法在回归实验上取得了明显的效果。
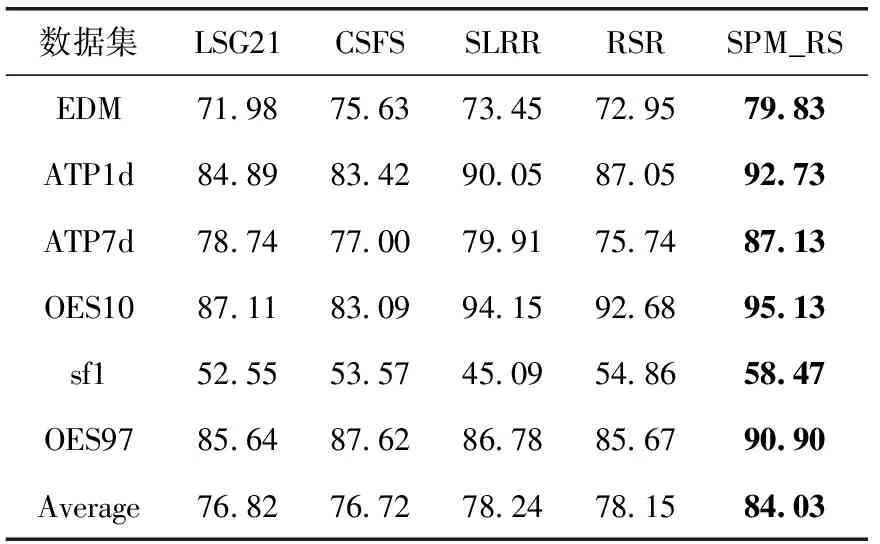
表2 aCC统计结果/%
实验结果表明SPM_RS算法在性能上优于4个对比算法。与SPM_RS相比,4个对比算法都没有采取有效的方法对样本进行选择,无法避免噪声和离群样本对回归模型的影响,从而影响模型的稳定性和准确性。本文算法不仅有效避免了噪声样本的影响,还保留了提取后的重要属性,使得算法拥有更好的性能。
4 结束语
本文提出了一种结合了基于自步学习多元回归分析算法(SPM_RS算法)用于回归分析。基于基本线性回归模型,利用自步学习选择训练样本,再结合稀疏属性选择理论对样本的重要属性进行选取。因此算法融合了自步学习和稀疏学习,既考虑了高维大数据对多元回归模型的影响,同时又有效避免了离群样本对模型训练带来的干扰。实验结果表明SPM_RS算法在回归分析中取得了较好的效果。在今后的研究中,我们尝试将自步学习引入其它的机器学习模型中来扩展自步需学习的应用范围。
