基于马尔科夫博弈的云代理与微云收益优化
2018-12-22张锋辉符茂胜何富贵
张锋辉,符茂胜,何富贵
(皖西学院 电子与信息工程学院,安徽 六安 237012)
0 引 言
由于移动设备的计算资源和电池容量极为有限,使得计算密集型应用在移动端的实施面临挑战,解决这一挑战有效方法是将计算密集型任务卸载到云上执行,这种方法称为移动云计算[1]。由于微云相比远程云计算中心距离移动设备更近,可以大幅度减少传输延迟,因此使用微云进行计算卸载是移动云计算的发展趋势[2]。
卸载任务到微云具有提高云计算效率、缩短任务传输时间等优点,但该方式也存在一些挑战:①移动设备通常无法确定那些是距离最近的微云,造成通信距离延长;②由于设备的移动性会导致它和微云之间的无线连接不稳定,造成通信中断;③部分微云会拒绝一些移动设备接入,造成任务无法卸载[3]。为解决微云存在的这些问题,一种新形式是云代理将该地区的微云进行联合为附近的移动用户提供云计算服务。云代理将任务送入距离最近的微云,当移动设备越出网络覆盖范围时,云代理能保证将结果送回。该系统结构如图1所示。

图1 系统架构
近期移动云计算中一个重要的研究方向是云代理和微云的虚拟机租用关系,其中Xie等使用双向博弈方法采用分布式多维价格机制提高微云中虚拟机利用率,从而提高云代理和微云的收益[4]。Qiu等采用斯坦伯格博弈的方法激励微云提供虚拟机资源给云代理使用[5]。Jin等提出了竞价机制提高微云资源利用效率,并保证竞价过程的不可欺诈性[6]。Liu等将微云的资源分配过程建模为半马尔科夫过程,并使用自适应多维价格方法提高微云的资源利用率[7]。另外一些研究采用博弈的方法或随机控制的方法提高双方收益[8-10],但这些研究主要考虑在单个时间片内虚拟机的租用问题,没有考虑长期内用户任务提交的随机性。
本文将云代理和微云的服务过程建模为排队过程,以云代理和微云实际利润为收益,把微云租赁虚拟机给云代理的过程转化为两者将任务送入虚拟机资源池而提高收益的过程,从随机性角度将这一过程建模为马尔科夫博弈,提出反向迭代算法实现博弈的纳什均衡。将该方法和云代理租用固定虚拟机方法进行对比,仿真结果表明采用马尔科夫博弈能明显提高收益。
1 云代理与微云关系模型
1.1 系统描述
如图2所示,本文仅考虑云代理租用一个企业微云资源情景,微云的资源划分为类型相同的虚拟机,它们构成虚拟机资源池,云代理和微云中均有一队列用于存储移动用户和企业内部用户提交的任务。将两者服务的过程划分为不同的时间片,单个时间片定义为微云完成所有任务需要的时间,每个时间片内两者将任务送入虚拟机资源池执行。为保证任务能够被快速处理,当微云资源池中虚拟机数量不能满足提交的任务量时,多余的任务将被送入其它微云进行计算,并支付相应费用[11]。
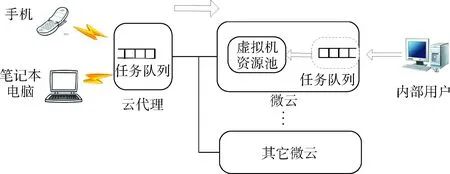
图2 任务执行过程
微云中虚拟机资源池被分为V个虚拟机,云代理中任务队列容量为F1,微云队列容量为F2。在时间片t内,云代理将b个任务放入虚拟机资源池运行,同时有c1个任务进入云代理的队列。在同一个时间片内,微云送d个任务进入虚拟机资源池,同时有c2个任务到达微云。因此在时间片t中,云代理队列长度s1小于队列容量,0≤s1≤F1。微云中队列长度s2小于队列容量,0≤s2≤F2。
1.2 系统状态和动作

(1)
(2)
系统以时间片形式运行,云代理和微云每个时间片分别送b和d个任务进入微云虚拟机资源池执行。但送入任务数不能高于队列中任务的个数,因此:0≤b≤s1, 0≤d≤s2。
将每个时间片中用户提交给云代理的最大任务量用c1max表示。内部用户提交至微云任务数的最大值用c2max表示,因此:0≤c1≤c1max, 0≤c2≤c2max。
1.3 系统转移函数
在不同时间片内,任务进入云代理和微云的数量会有一定随机性,把该系统任务到达的过程描述为泊松过程[12-14],任务的平均到达率为λ。因此云代理在状态为s的条件下将b个任务送入到虚拟机资源池后队列中的数量的概率为p(c1),当进入队列的数量多于队列剩余的空间时,多余的任务将被丢弃,在此情况下云代理队列中任务数量的转移函数为
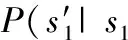
(3)
在时间片t中,微云将d个任务送入虚拟机资源池运行。同时内部用户提交的任务进入队列,当队列满时微云将任务送入其它云中运行并支付费用,因此微云状态变量s2在微云动作d下的转移概率为

(4)
在系统中状态变量s1和s2相互独立,S′表示下一个时间片系统的状态,因此我们可以得到在云代理动作b和微云动作d下系统的转移概率
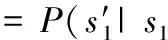
(5)
1.4 云代理和微云的即时收益函数
微云对虚拟机资源池的管理需有一定成本,本文将其描述成学习曲线模型,当运行的虚拟机数量增加时,管理单位虚拟机的边际成本会以固定因子下降[11]。使用Uo表示管理运行的虚拟机所需成本,管理首个运行的虚拟机所需成本为co,φ表示微云的学习因子。因此管理运行虚拟机所需的总成本是
(6)

(7)
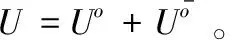
云代理以单个虚拟机价格为p收取用户费用,且以每个虚拟机价格为q支付给微云。微云内部用户可免费使用虚拟机资源。每个时间片t,云代理送b个任务到虚拟机资源池执行,同时微云也将d个任务送入执行,当d+b>V时,多余的任务将别送入其它云执行,并需支付相应的费用,其它云虚拟机单价使用r表示。多余的任务数量为V-b-d,使用γ1表示云代理送入任务过多时的惩罚因子,γ2表示微云送入任务过多时的惩罚因子,并将它们表示如下

(8)
R1代表在时间片t内云代理的即时收益,可用如下公式表示
(9)
根据微云送入任务的多少和虚拟机资源池的使用情况,将其收益分为4种类型表示
(10)
式(9)、式(10)描述了在每个时间片内云代理和微云的收益。由于用户提交任务具有随机性,在单位时间内的收益不能表示两者的长期收益,因此需对两者的长期收益进行优化。
2 马尔科夫博弈
云代理和微云分别将任务送至虚拟机资源池,由于任务到达的随机性,各自队列中任务数量呈现马尔科夫转移特性,因此可采用马尔科夫博弈的方法对两者关系进行建模。使用W1表示云代理的长期收益,W2表示微云的长期收益,β表示博弈的折扣系数。π(S,b)表示时间片t内系统状态为S下云代理采用动作b的概率。π(S,d)表示时间片t内系统状态为S下微云选择策略d的概率。因此我们得到长期的折扣收益为
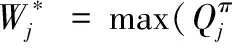
max(Rj+β∑T(S′|S,b,d)∑π(S′,b′)
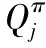
subjectto(1)(2)
0≤s1≤F1
0≤s2≤F2
0≤b≤s1
0≤d≤s2
0≤c1≤c1max
0≤c2≤c2max
(11)
3 系统分析和算法设计
在系统运行的每个时间片内,云代理和微云根据队列中任务的个数选择相应任务量送入虚拟机资源池,因此在每个时间片内博弈双方获得的收益不同,所以在每个时间片中系统的收益不同,因此该博弈是变和马尔科夫博弈。此种类型的马尔科夫博弈具有纳什均衡策略[15]。本文根据此类博弈的特性设计了反向迭代算法使其达到ε纳什均衡。
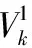
反向迭代算法:
输入:p,q,r,G,F2,F1
输出:云代理和微云在每一个状态的最优策略
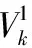
Repeat:
(1)在每个系统状态和最优动作d*下计算云代理的最优动作,使用下式
b*(S)= argmax∑T(S′|S,b,d*)
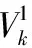
(2)计算在最优动作b*下云代理的最优的收益
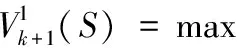
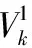
(3)根据云代理的最优动作b*在状态S下计算微云的最优的动作d*,使用如下公式
d*(S)= argmax∑T(S′|S,b*,d)

(4)根据微云最优的动作计算最优收益


(5)计算云代理和微云本次迭代和上次迭代所有状态的均值
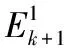
(7) if ΔV1≤ε,ΔV2≤ε
returnb*,d*
end repart
else
k=k+1
goto 1
end if
4 实验仿真
首先仿真估计该反向迭代算法的收敛性,而后比较该方法性能。
在仿真过程中,设置折扣因β=0.85,算法的终止条件为ε=1e-4,云代理中任务的平均到达率为λ1=12,微云中企业内部用户任务的到达率为λ2=8,系统中虚拟机个数为20。云代理以单位虚拟机价格为0.4 $收取移动用户费用,以每个虚拟机价格0.32 $租用微云虚拟机资源池,当任务量溢出时两者将多余任务送入其它云进行运算并以单价为0.48 $支付给其它微云,首个运行的虚拟机所需的管理成本为0.06 $,首个空闲虚拟机所需管理成本为0.03 $[12]。
由图3可看出当采用反向迭代算法时,当迭代到59次时两者的收益收敛于ε纳什均衡。在经过20次迭代后两者收益均值趋于稳定,结果表明该采用反向迭代算法能很好达到博弈的均衡点。
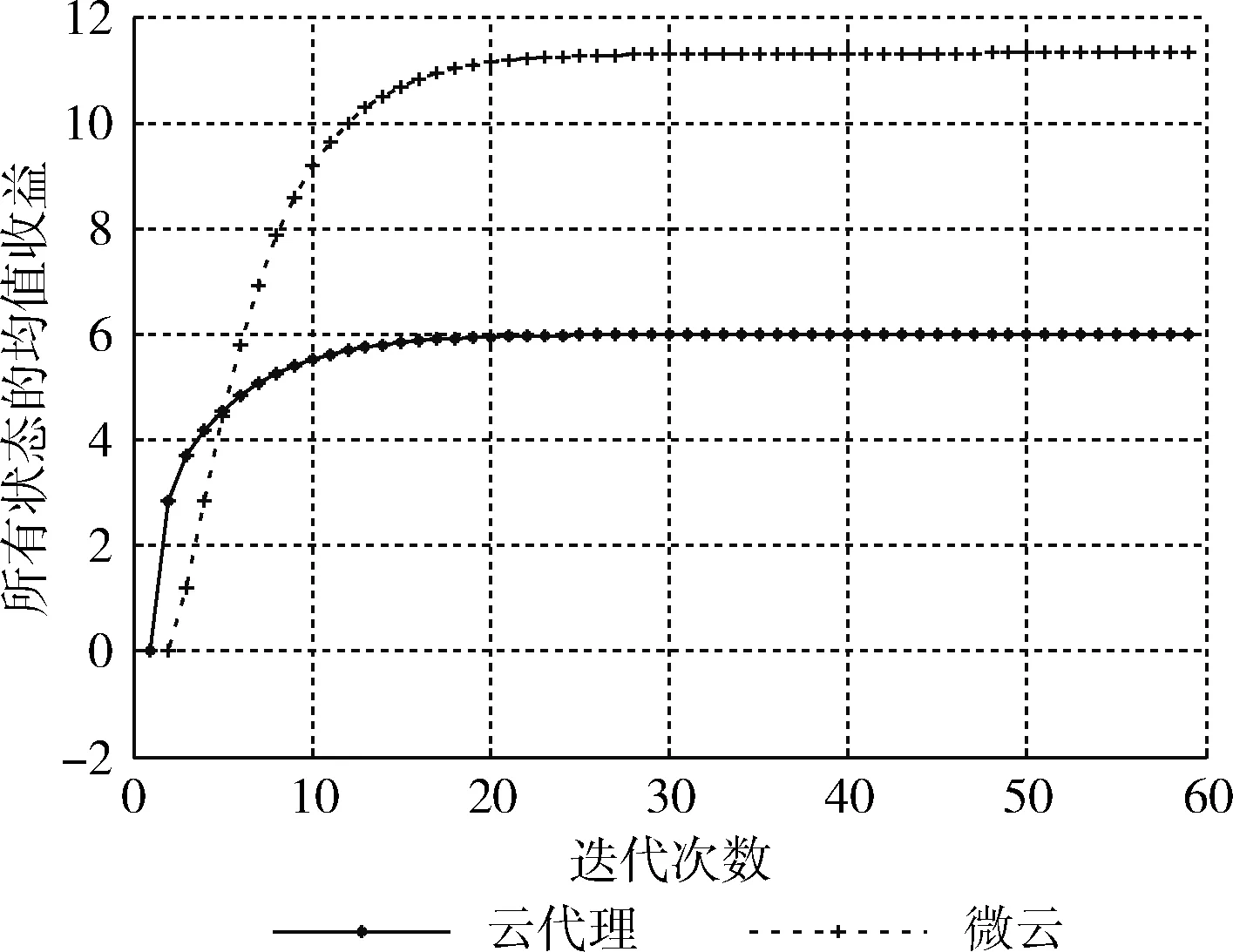
图3 均值的收敛性
为了和马尔科夫博弈的方法进行对比,设计了云代理租用固定虚拟机数量的方法,租用量为微云虚拟机数量的40%。图4为两种方法的比较。从图4中可以看出相比租用固定虚拟机的方法使用马尔科夫博弈能够明显提高云代理和微云的收益,并且系统收益明显提高。

图4 马尔科夫博弈和租用40%虚拟机数量的收益比较
将马尔科夫博弈的方法和微云租用其虚拟机60%的方法进行对比,结果如图5所示。图中的收益是收敛时博弈双方及系统的折扣收益。从中可以明显看出采用马尔科夫博弈方法使博弈双方提高收益的同时也提高了系统收益。
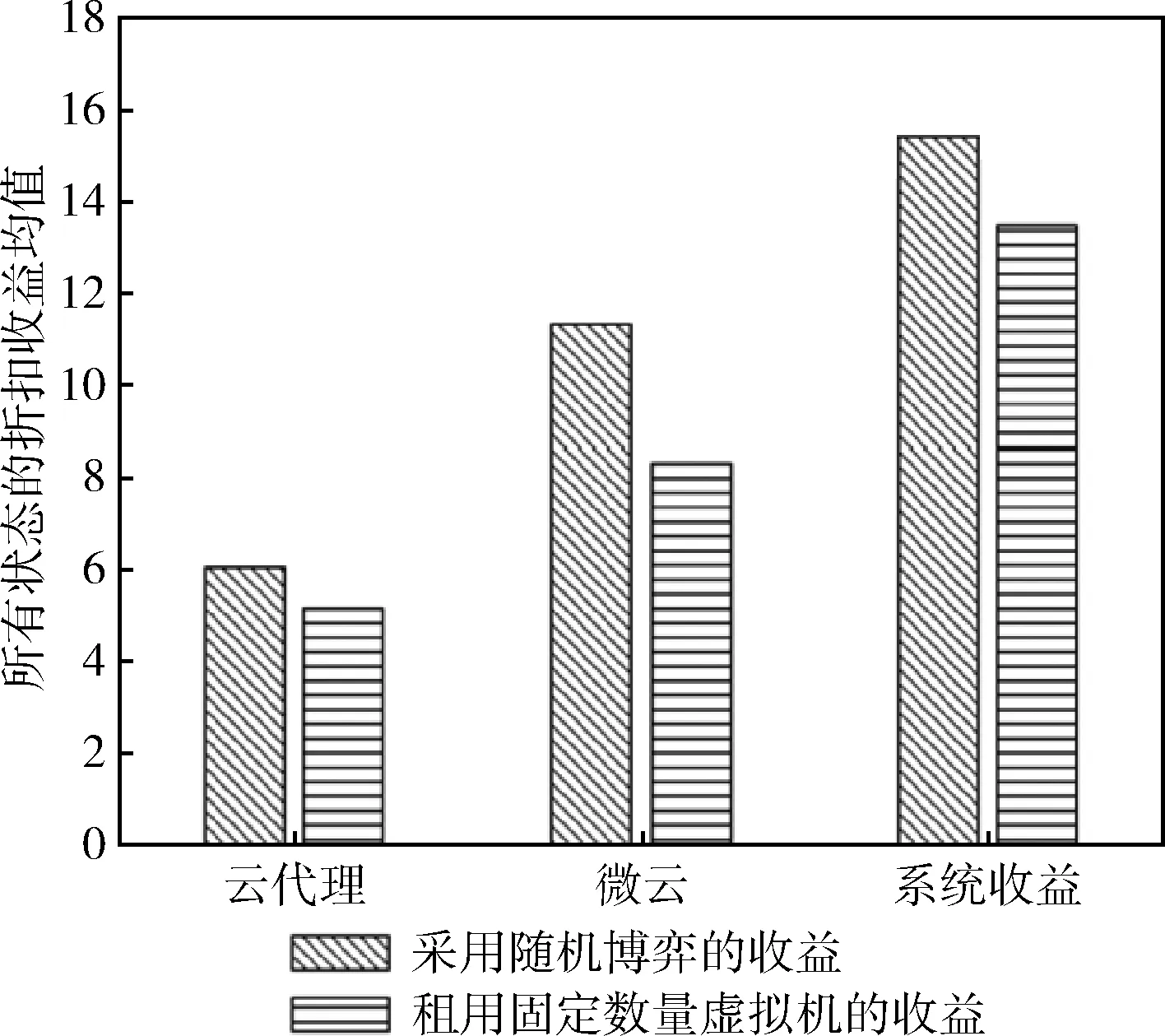
图5 马尔科夫博弈和租用60%虚拟机数量的收益比较
5 结束语
本文根据在移动云计算中任务提交的随机性,将云代理租用微云虚拟机的收益获得问题转化为两者为使各自收益最大化而送任务到虚拟机资源池执行的过程,并提出了反向迭代算法达到了该博弈的纳什均衡点,最后仿真结果表明采用马尔科夫博弈的方法能明显提高云代理和微云收益,具有一定使用价值。但是该研究仅针对同一类微云,对于不同性质的微云和处于不同地区的微云如何提高其收益是下一步的研究方向。
