塔式GPCA张量线性子空间图像模式低秩识别
2018-12-22申希兵
申希兵,韦 容,杨 毅
(1.钦州学院 资源与环境学院,广西 钦州 535000;2.钦州学院 人文学院,广西 钦州 535000;3.广西科技大学 软件学院,广西 柳州 545006)
0 引 言
在图像模式识别[1,2]中,维度降低可实现无损前提下的数据处理量的降低,但是降维存在的最大问题是,会导致图像模式的拓扑和几何特征信息丢失[3]。
很多研究人员都致力于数据降维算法的研究,文献[4]提出多值属性的图像金字塔降维技术,采用多值来构造多分辨率金字塔骨架;文献[5]提出基于图论的3个金字塔方法,可保留图像的几何性质;文献[6]开发了边缘特征向量方法;文献[7]开发了奇异值分解(SVD)图像编码系统;文献[8]提出广义主成分分析(GPCA)的图像压缩方法;文献[9]研究显示从高维欧氏空间到低维欧氏空间的嵌入点存在低失真可能性;文献[10]实验结果表明,随机映射可保持低维子空间中的原始数据与高维数据之间的距离;文献[11]指出构建随机矩阵的条目必须至少4组,且相互独立;文献[12]建立了对称正定矩阵的几何感知降维方法,其学习方法不依赖于流形的切空间近似。此类文献较多,不再赘述。
上述图像模式识别文献存在的问题有:①理论分析不够深入,缺乏理论佐证;②降维过程存在的图像模式的拓扑和几何特征信息丢失问题未得到有效解决。对此,为解决上述问题,本文提出一种基于塔式随机映射广义主成分分析(GPCA)的张量线性子空间图像模式低秩识别方法,从理论分析和拓扑、几何特征信息保持角度进行算法设计,并进行了有效性验证。
1 塔式变换与随机映射
1.1 塔式变换
利用因子σ定义下采样操作Dσ
g(x,y)=Dσf(x,y)=f(σx,σy)
(1)
利用因子σ定义上采样操作Uσ

(2)
上述下采样和上采样操作存在以下特性:
特性1 部分等距特性:这些操作满足关系
(3)
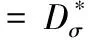

(4)
降维算子R的对偶算子E可定义为

(5)
根据式(1)可知,降维是通过卷积核ωσ的平滑函数实现,在实际应用时选取σ=2。
对于一个非扩张映射φ,其满足
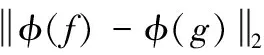
(6)
式中:φ(f)≠λf,则可得定理1,具体如图1所示。

图1 函数及其非扩张映射夹角
定理1 设定∠f,g为f和g在Hilbert空间上的夹角,其满足
∠(φ(f),φ(g))≤∠(f,g)
(7)
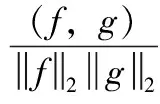
(8)
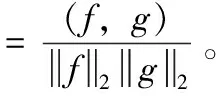
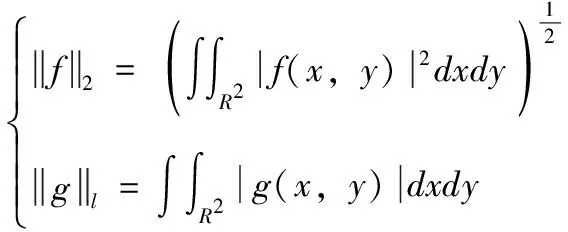
(9)
对于f(x,y)和g(x,y)之间的卷积h(x,y)=g(x,y)*f(x,y),可得如下推论:
推论1 对于卷积能量,可得如下特性

(10)
对于线性算子R,如果Rf≠0,则当f∈L2,g∈L2时,存在关系

(11)
定理2 塔式变换是线性扩张和降维映射。
证明:根据定义可知,对于两个二维图像,通过塔式变换线性操作可将原始尺寸的图像降低到1/4。因此,这个操作线性降维映射。同时根据式(11),塔式变换是非扩张映射。
根据上述特性,可得到以下特性:
特性2 假阳性识别:对于本来很大的模式相似性,定理2通过塔式变换可提供比原来的模式更大的相似性。然而,对于原来很小的模式相似性,塔式变换可提供更大的相似性,此特性可有效对假阳性进行识别。
对于采样函数fij=f(i,j),下采样Dσ和对偶操作Uσ可扩展为
(12)
此外,塔式变换线性降维算子R和其对偶算子E可扩展为
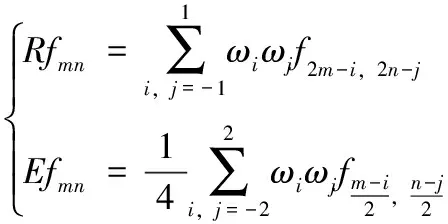
(13)
其中,ω±1=1/4和ω0=1/2。此外,对整数m-i和n-j进行求和操作。这两个操作涉及的图像大小降维和扩展。作为非扩张映射,塔式变换可对O1/2n的n阶张量进行压缩,并可保持张量数据的微分几何结构。
1.2 随机映射
塔式变换是一种度量嵌入方法,可近似保留原空间中的点与点之间的距离。此外,对于任意一个点集,塔式变换可保留点角集、卷积单形和光滑曲线及流形的长度。图2(a)~图2(c),显示了存储的距离,角度和体积,以及塔式变换流形。
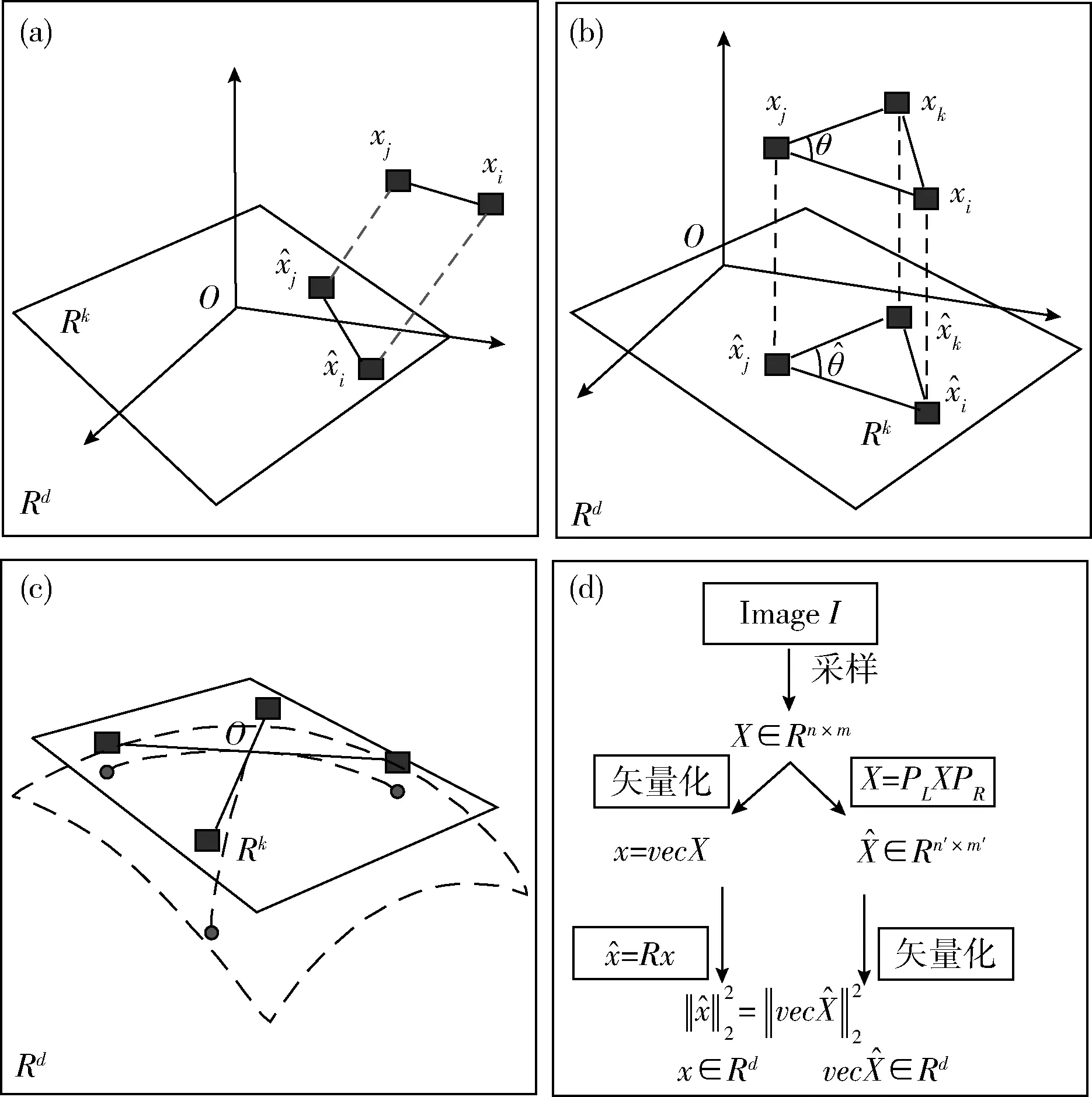
图2 图像模式识别映射情形

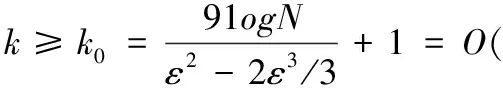
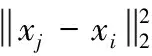
(14)
式中:i,j=1,2,…,N。从模式识别的角度来看,特性3表明该映射近似保留模式的相似性,而不受类型的模式或其分布的影响,虽然映射不能保存图像的几何形状。
对于d维欧式空间的N个点集,k≤d,令R为k×d正交矩阵,形式为
(15)
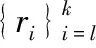
(16)


(17)
对于上述随机映射,可得如下定理:
定理3 随机映射是线性和拓扑保持降维映射。

(18)
该下界表明,维度K的低维空间与D维原始空间是独立的。下界k0来自马尔可夫不等式,在大多数情况下,比实际误差ε要小得多。对于标准的随机线性映射,可得如下定理:

(19)
随机矩阵R定义一个独立的数据集X的k维随机子空间。随机线性映射降维并未考虑数据分布。密集的随机矩阵生成需要的计算和存储成本为Okd。此外,N个点映射需要计算和存储成本为OkdN。实际计算中,所使用随机线性映射的计算和存储成本为Odlogd。
2 模式张量的线性降维
2.1 拓扑和几何表示
图2中给出图像模式识别中的3种映射情形,尽管构造顺序结构,但会在度量空间中嵌入数据。因此,可利用弱和强条件对阶条件要求进行替换。一般情况下,在线性降维操作中,强的和偏向性的条件不成立。线性降维方法中,随机映射满足图像模式识别所需的弱条件,而其它方法不满足。
作为非线性降维方法,内核方法通过映射函数Φ将数据映射到高维空间。内核方法满足条件
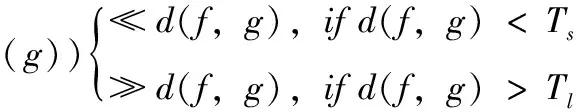
(20)
其为非线性映射,对于Ts
内核方法实际计算,给出两个数据在高维空间投影的内模,而不是在高维空间中的范数或距离。例如多项式函数
k(f,g)=(Φ(f),Φ(g))=((f,g)+1)p
(21)
高斯径向基函数为
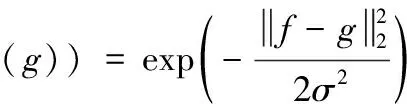
(22)
在高维空间中给出f和g的内模。该函数给出对应距离比阈值T更大的内模。基于内核,在高维空间中执行线性降维,并获得在原来空间中的非线性映射。
2.2 二维随机映射

(23)

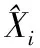

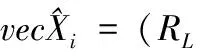
(24)

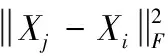
(25)


(26)
通过矩阵Xi的Frobenius范数,替换vecXi的欧式范数,可得上述定理成立。
通过将二维数组扩展为二阶张量,可减少任意维数据张量的维数。通过二维随机映射在函数空间保存张量的拓扑结构。
2.3 广义主成分分析
(27)
其中,U=[u1,…,um],V=[vl,…,vn]通过最小化的标准

(28)
和最大化准则获得
(29)
其限制条件为
UTU=Im,VTV=In
(30)
式中:Im和In为单位矩阵,通过计算特征值分解问题的极值可导出
(31)
MV=V,NU=U∑
(32)
式中:∑∈Rm×m,Λ∈Rn×n是满足关系λi=σi的对角矩阵
(33)

Yi=(UP1)TXi(VP2)=LTXiR
(34)
其中,P1和P2为映射矩阵U和V的基向量,则式(34)所示矩阵为图像压缩的二维随机映射方法,该方法采用二维PCA变换形式为
Yi=XiR
(35)
为实现上述奇异值分解的指标优化,所提算法见伪代码1。

伪代码1:广义主成分分析的迭代最小二乘算法(1)输入:一组张量Xi∈m×n{}Ni=1。模式1和2的维度降低数k1和k2,最大迭代数K;(2)输出:一组投影矩阵PL,PR{};如果k1=m、k2=n,则PL,PR{}给出全投影,否则,它给出了全投影截断。(3)通过M(0)r=1N∑Ni=1XiXTi和M(0)c=1N∑Ni=1XTiXi的特征分解,计算初始投影矩阵P(0)L和P(0)R。(4)通过选择M(0)r和M(0)c的k1和k2个特征向量,构建投影矩阵;(5)计算ψ0=∑Ni=1P(0)TLXiP(0)R2F;(6)begin loop(7) for k=1,2,…,K(8) 选择M(k)r=1N∑Ni=1XiP(k-1)RP(k-1)TRXTi的k1个特征向量,计算P(k)L;(9) 选择M(k)c=1N∑Ni=1XTip(k-1)TLP(k-1)LXi的k2个特征向量,计算P(k)R;(10) if ψk-ψk-1<η,ψk=∑Mj=1P(k)TLXiP(k)R2Fbreak;end(11)return PL=P(k)L、PR=P(k)R;
2.4 张量的子空间低秩逼近分类
对于矩阵X,设定PL和PR为正交投影,则X到Y的正交投影为
(36)

(37)


(38)
则可得G∈Ck(δ)。
设定Rd为d维欧氏空间,定义内积f,g,令f∈Rd,Pk分别为第i类模式和操作算子,其中第i类模式可定义为
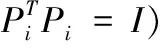
(39)
由于模式扰动,可定义类别i形式为
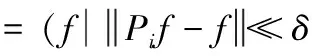
(40)
其中,δ表示小扰动模式。对于输入g∈Rd和类别Ci,分别定义相似性和分类标准
θi=∠(Ci(δ),g),0<θi<∃θ0→g∈Ci(δ)
(41)
定义输入模式g和模式空间的角度为
(42)
输入模式和模式空间之间的角度表示两者之间相似性。对于输入g∈Rd构建
(43)
由此可得
θi=∠(Ci(δ),Cg(δ)),θ<θi<∃θ0→Cg(δ)∈Ci(δ)
(44)
其中,CgCk(δ)∩Cg(δ)≪δ。为fi∈Ci构建操作算子Pi
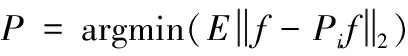
(45)
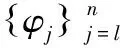
(46)
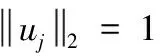
图3显示了基于塔式变换降维,主成分分析和二维张量主成分分析子空间低秩逼近分类过程。塔式变换和PCA变换都是酉变换。
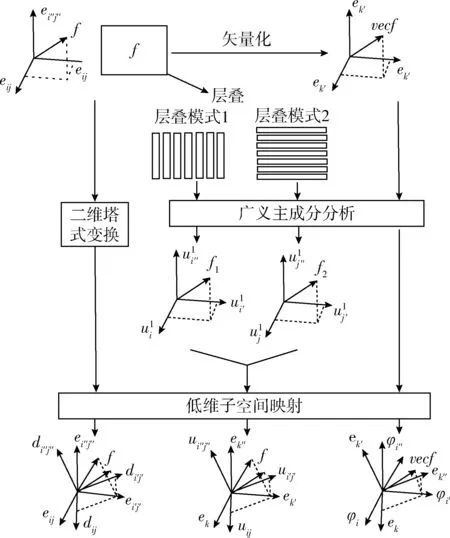
图3 子空间低秩逼近
3 实验分析
为评价所提图像模式识别的维数约简方法性能,实验对象选取CALTECH101目标检测数据集、YaleB人脸数据库、ORL人脸数据集和ETL9G中文字符集,具体如图4所示。

图4 测试数据集
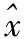
(47)
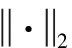
(48)
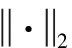
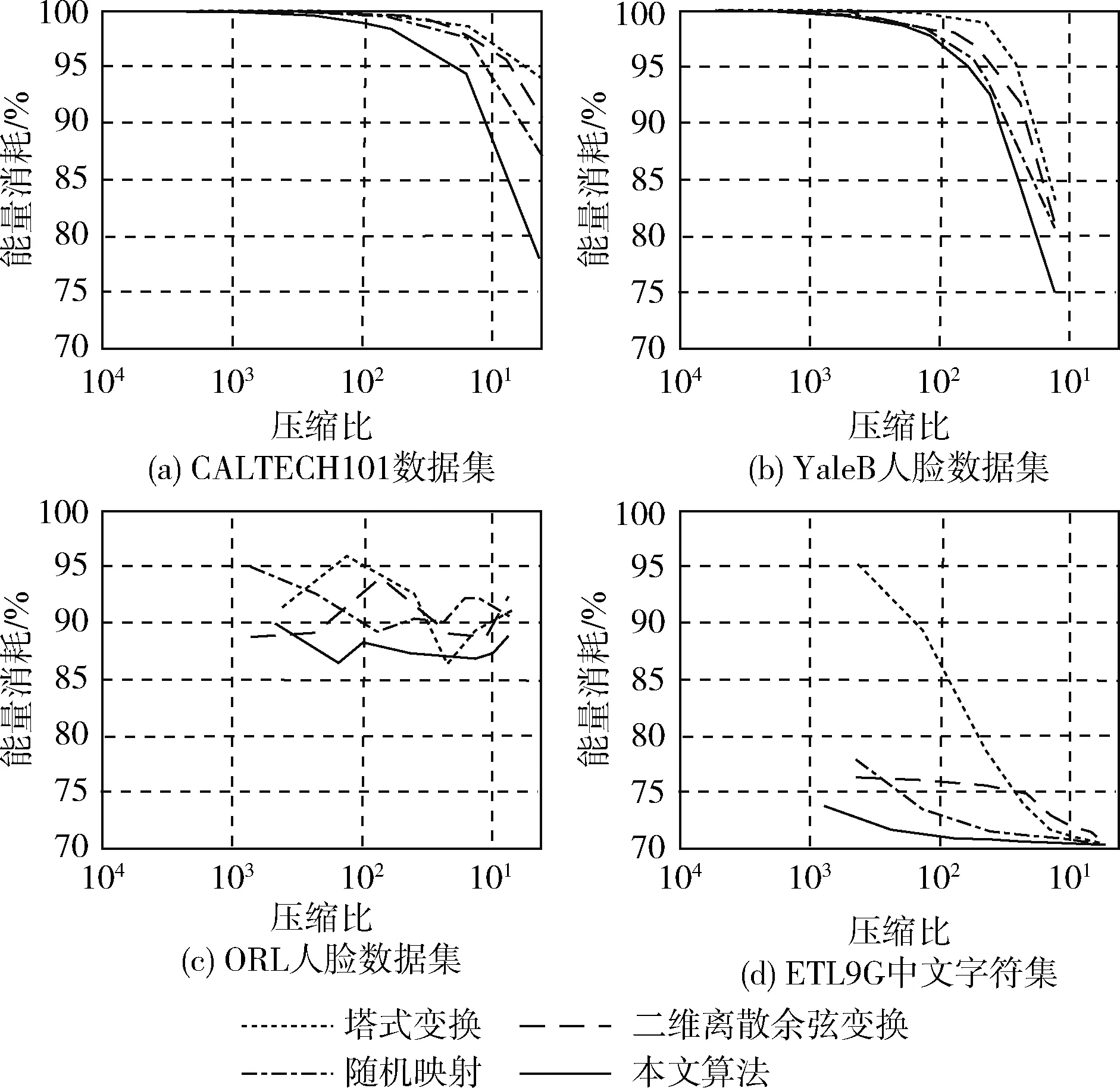
图5 能量消耗对比

图6 图像间距相对误差均值
由图5能量消耗对比曲线可知,塔式变换所需要的消耗指标最大,其次为二维离散余弦变换,第三是随机映射,而本文算法所需要的能耗指标最低,这表明所提算法在计算资源消耗上要少于选取的3种对比算法。由图6图像间距相对误差均值对比曲线可知,在CALTECH101目标检测数据集和ETL9G中文字符集中,塔式变换相对误差均值最大,其次为二维离散余弦变换,第三是随机映射,而本文算法图像间距相对误差均值指标最低,在YaleB人脸数据库和ORL人脸数据集上,算法间相对误差均值指标在压缩比取值较小时,存在交叉现象,但是整体上本文所提算法的相对误差均值指标更低,这表明所提算法在原数据拓扑和几何特征保持能力上要优于选取的3种对比算法。
为更加直观的验证所提算法在图像模式识别中的性能,选取识别率和计算时间作为对比指标,对比算法选取文献[13,14]算法,这两种算法均为随机映射算法的改进版本。实验硬件参数:CPU i5-6200U,内存6G ddr3-1600,系统win7旗舰版,硬盘为浦科特M6S+ 128G固态硬盘,实验对象选取上述YaleB人脸数据库和ETL9G中文字符集,实验对比数据见表1。

表1 识别率和计算效率对比
根据表1数据可知,在识别率指标中,本文算法在YaleB人脸数据库和ETL9G中文字符集上的识别率分别为91.5%和94.1%,要稍高于文献[13,14]两种对比算法,在计算时间指标中,本文算法在YaleB人脸数据库和ETL9G中文字符集上的计算时间分别为7.6 s和6.5 s,要优于文献[14]算法,同时与文献[13]算法相差不大。上述实验结果验证了所提算法在识别率和计算时间指标上的性能优势。
4 结束语
本文提出一种基于塔式随机映射广义主成分分析(GPCA)的张量线性子空间图像模式低秩识别方法,推导出随机映射所具有的线性和拓扑保持的降维映射特性,并基于塔式变换降维,随机映射和GPCA构建张量子空间低秩逼近分类过程,实验结果表明,所提算法在能量消耗等指标上要优于选取的对比算法。
同时应该看到,在计算识别率指标上,所提算法还有进一步提升的空间,其在在YaleB人脸数据库和ETL9G中文字符集上识别率与文献[15]所提算法识别率相比,并无绝对优势。
