基于PLFT及图像融合的卫星河流识别
2018-12-22冷凯群
冷凯群
(北京工业大学 软件学院,北京 100124)
0 引 言
卫星图像中的河流自动监测具有重要的应用价值,如水资源的监测和评估、洪水预测、水污染检测、及GIS数据库更新等。计算机视觉中的目标识别和检测的主要任务就是依靠特征提取的分类器的设计。一些常用的图像特征包括灰度特征、彩色特征、形状特征、结构特征及纹理特征等;常用的分类器包括支持向量(SVMs)、多层感知器、最近邻域分类器等[1]。
随着理论研究的加深和技术的进步,近些年国内外学者提出局部图像特征并将其广泛地应用于计算机视觉、图像处理及模式识别领域[2-4]。在局部图像空间内具有的对光照、尺度、位置、遮挡等的不变性是局部图像特征能得以成功应用的关键,而这种属性在全局图像空间中是不具有的,因此局部图像特征比一些全局图像特征(如:基于主元分析(PCA)的特征)更具有模式鉴别能力。在模式识别研究领域,基于k近邻(kNN)思想的分类器是最简单也是研究时间最长的一类分类器。文献[5]提出了一种基于增大判决边缘距离的大间隔近邻(large margin nearest neighbor,LMNN)分类器算法,LMNN通过从训练样本中学习马氏距离(Mahalanobis)达到模式分类的目的——属于同一类别的样本总是在k邻域内,而不同类别的样本被一个较大的判决边缘距离隔离开。该方法的实验结果表明,LMNN分类器在5个大型数据库中的3个能取得比SVM更好的分类效果,但是其仍需要有较大的改进。
本文提出了一种基于融合的方法用于提取卫星图像中的河流区域,该方法通过对监督分类的结果和无监督分割的结果进行融合而得到最终的结果。在监督分类的方法中本文提出了一种局部图像特征算法,即基于主元分析的局部傅立叶变换特征(PCA-based local Fourier transform,PLFT)。与现有方法相比,PLFT对图像的纹理信息和颜色信息具有更好的模式鉴别能力,能更准确的对卫星河流的背景和颜色信息进行分类识别。
1 本文识别算法
1.1 所提PLFT特征算法
1.1.1 局部傅立叶变换特征
Zhou等[6]提出了一种基于局部傅立叶变换(local fourier transform,LFT)的图像纹理特征描述算子用于纹理分类和图像分割。Yu等[7]提出了一种改进的LFT,该特征描述算子的新颖之处在于计算傅立叶系数的一阶和二阶矩,而非文献[6]中那样计算量化后傅立叶系数的直方图。LFT在处理灰度图像时,使用8个LFT模板计算得到一个维数为16的特征数组;当该算法进一步应用于处理彩色图像(如HSV)的每一个彩色分量时,能得到一个维数为48的特征数组,并取得比灰度的LFT特征更好的图像识别或分割效果。
图1是一个3×3的局部图像I(x,y),x=1, …,L-2和y=1, …,M-2,这里原始图像大小是L×M,中心点是(x,y),8个邻域像素点被标注为Pn,n=1, 2, …, 8。式(1)计算(x,y)的局部傅立叶变换系数
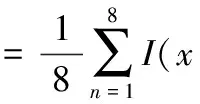
(1)
其中,FI(k)表示灰度共生属性以及它们的空间分布[6],n是8个邻域像素点的编号。

图1 3×3的局部图像区域
1.1.2 PLFT特征提取流程
目前,有效将LFT系数转化为特征描述算子向量的方法有两种:一种是计算系数量化后的直方图;另一种是计算系数的一阶和二阶矩。而文献[7]的结果表明后者的图像特征描述能力要优于前者,所以本文采用后者的方法。接下来,首先介绍计算LFT系数的一阶和二阶矩的过程,然后由此推导提出一种新的局部特征描述算子,即基于主元分析的局部傅立叶变换特征(PCA-based local Fourier transform,PLFT)。
F=[f1,f2,…,f81]∈R8×81
(2)
沿F的水平方向计算每行的均值就得到系数的一阶矩:M=[m1,m2,…,m8]∈R8,其中

(3)
系数二阶矩是计算水平方向每行的方差,即V=[v1,v2,…,v8]∈R8,其中
(4)
最后,通过级联向量M和V得到一个维数是16的LFT特征向量:Xlft=[M,V]∈R16。
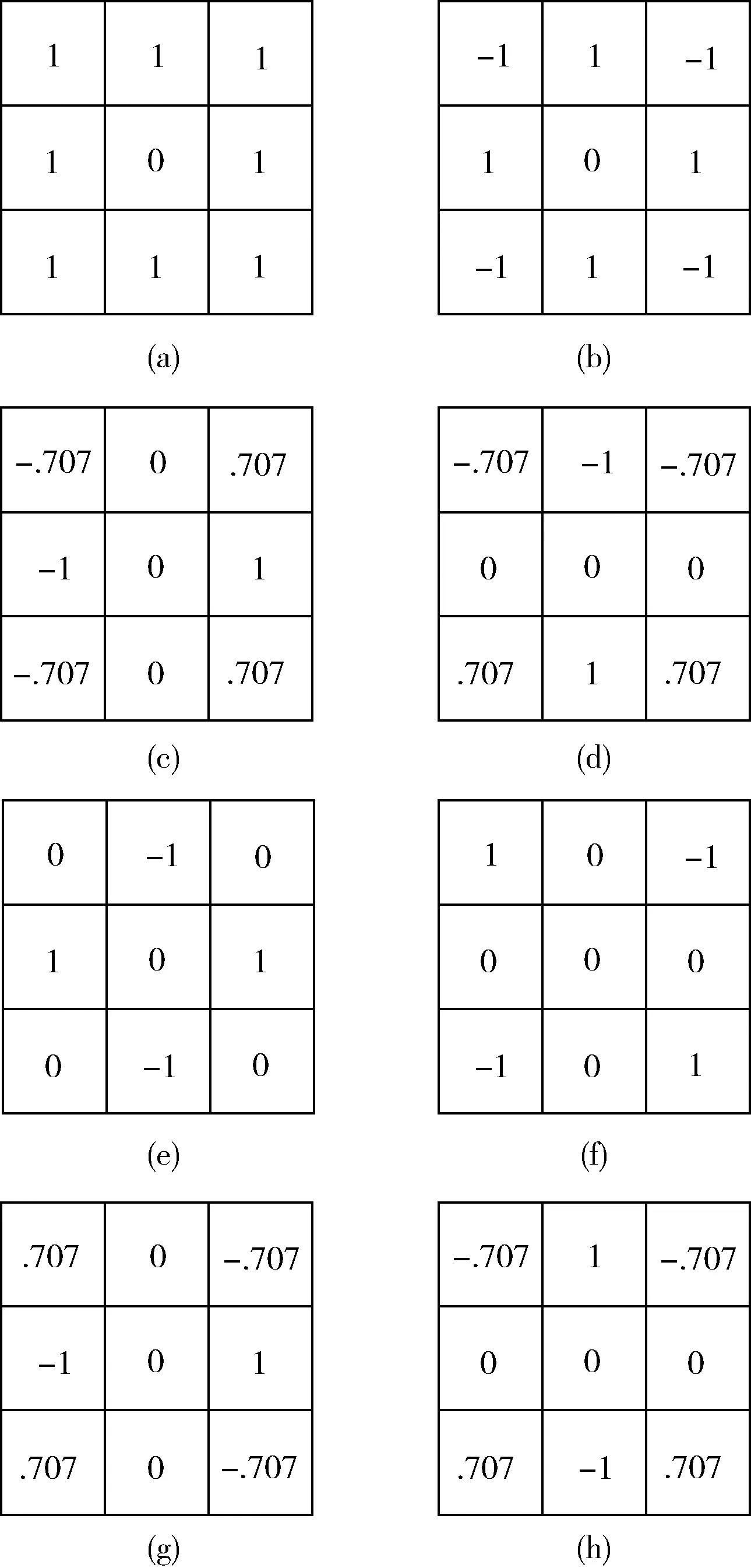
图2 8个计算LFT系数的模板[7]
均值和方差是统计方法描述样本数据的两个基本分布特征,此外,另一个常用于揭示数据内在分布特征的方法是主元分析法,它的第一主元(最大的特征值)揭示了数据分布中最大可能的方差,而第二主元是数据分布中下一个最大可能的方差,以此类推,并且不同的主元之间它们的方向是正交的。因此,可以利用主元分析方法在LFT系数矩阵中提取更有用的特征用于描述图像。
假设在整个训练样本中总共有N个图像窗口,那么可以组成一个更大的LFT系数距阵
F=[F1,F2,…,FN]∈R8×Nm
(5)
这里m是每个图像窗口里可用于计算LFT系数的像素点,如前面的81个像素点。对F进行奇异值分解
F=UDWT
(6)
这里U和W分别是左奇异值向量矩阵和右奇异值向量矩阵,D是对角矩阵包含了奇异值,而非零奇异值的平方就是8×8矩阵FFT的非零特征值。
在特征值中,由于数据中的噪声和样本数量不足,较小的值通常偏离数据分布的真实方差[8]。为了避免主元空间中的不稳定性,会把特征值较小对应的主元向量从主元空间中去除掉,通常只保留前面k个较大的主元向量组成主元空间U,这里的k可以通过设定特征值能量的98%来确定。通过主元分析方法,可以将F中的每个Fi转化成具有低维的形式
Fi=UTFi∈Rk×m, (k<8)
(7)
然后沿水平方向计算Fi每行的均值,Mpca=[m1,m2,…,mk]∈Rk。把3个向量M,V,Mpca级联起来就形成了一个新的图像描述特征,即基于主元分析的局部傅立叶变换特征PLFT
Xpca_lft=[M,V,Mpca]∈R16+k
(8)
由于加入了主成分分析元素,PLFT能够更有效地识别出占主要地位的有用信息并忽略占次要地位的干扰信息,因此,与文献[6]中所提的LFT方法相比,PLFT对图像的纹理信息和颜色信息具有更好的模式鉴别能力。
1.2 LMNN分类算法
大间隔近邻算法(LMNN)由Weinberger等提出,该算法基于K近邻算法改进,具体理论可参见文献[10]。其学习一种马氏距离度量方式
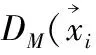
(9)
式中:M=LTL为半正定对称矩阵,用于最小化每个训练点和它的K个最近邻中类标签相同的点,以及最大化类标签不同的点,其构造代价函数
ε(M)=(1-μ)εpull(M)+μεpull(M)
(10)
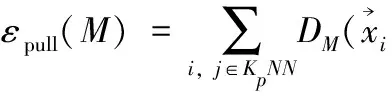
(11)
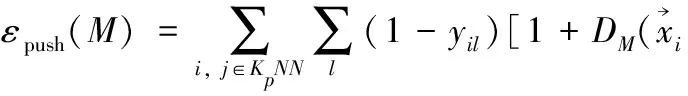
(12)
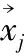
2 卫星图像河流检测流程
2.1 图像颜色空间转换
在计算机视觉领域,彩色特征已经被广泛地研究以提高目标和场景识别中算法的光照不变性和分类鉴别能力[9]。L*a*b*彩色空间也叫做CIELAB彩色空间或CIE L*a*b*彩色空间,是常用来描述人眼可见的所有颜色的最完备的彩色模型,它的3个基本坐标分别表示图像的颜色亮度,在红色/品红色和绿色之间的位置及它在黄色和蓝色之间的位置。在卫星图像中大部分河流区域呈现出黑色或深蓝色,而背景一般是绿色或棕色的,利用L*a*b*彩色空间,可以量化卫星图像中河流和背景之间的颜色视觉差别,针对这种特点本文选取在L*a*b*彩色空间中进行河流的提取和分割。因此,在后续处理之前需要首先把彩色卫星图像从RGB空间转化为L*a*b*彩色空间,如图3(a),图3(b)所示。
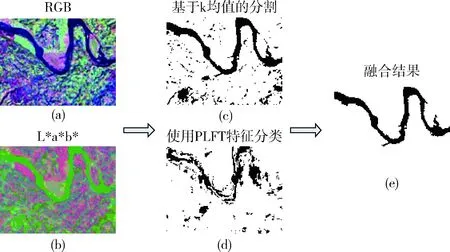
图3 本文算法的流程
2.2 有监督PLFT特征分类
彩色卫星图像在转化到L*a*b*彩色空间后,对它的每个彩色分量提取PLFT特征,这样对每一个图像窗口可获得一个维数是3×(16+k)的向量组。在有监督的分类算法中,使用PLFT特征和LMNN分类器把每个像素分类成河流和背景两类。由于要处理L*a*b*空间的3个分量,为了减少计算量这里并非分别计算3个投影矩阵U(见式(7)),而是把3个彩色空间分量的LFT系数矩阵级联起来组成一个矩阵F∈R24×Nm,以得到一个单独的投影矩阵U,这样PLFT特征的维数就是3×16+k而不是3×(16+k)。值得注意的是,在训练和测试过程中需要使用同一个投影矩阵U。
有监督分类学习过程中的训练样本是裁剪出的11×11的图像窗口,它们包含了河流区域(正样本)和背景区域(负样本),使用类别标注后的样本训练一个LMNN分类器,然后用训练完成的LMNN分类器来对需要处理卫星图像进行河流识别。有监督分类的结果如图3(d)所示。
2.3 无监督k均值聚类分割
在无监督的方法中,使用k均值聚类方法对L*a*b*空间的3个分量同时聚类,根据理论经验这里聚类中心数选择为5,然后把具有最小L*值的中心选为河流像素点的聚类中心,分割的结果如图3(c)所示。
2.4 融合检测
观察图3(c),图3(d)所示的两类识别结果可以发现,无监督聚类的方法取得了较高的正确率,即大部分河流区域被分割出来,但同时也有较高的错误率,即把很多的背景像素也识别为了河流区域。而有监督学习的方法由于严重地依靠训练样本,它的分类正确率不高,即一些河流像素被分类成背景。这是因为卫星图像中背景区域的面积远大于河流面积,故而很难获得足够多的正样本来训练LMNN分类器,所以在对新样本进行分类测试阶段一些河流的像素点不能够被正确的分类。但同时这种方法有较低的错误率,只有少部分背景被分类成河流。
基于上述的特点,为了提高本文算法的性能,提出通过融合的方法得到河流的识别结果,即同时使用有监督PLFT特征分类和无监督k均值聚类的图像分割的方法提取卫星图像的河流区域,最后把两种方法的结果进行融合得到最终的结果。融合检测的效果如图3(e)所示。
3 实验研究
3.1 PLFT分类性能分析
为了分析本文所提PLFT特征在目标分类中的有效性,从Google Maps中随机选取50幅包含河流信息的卫星图像作为实验样本图像。图4所示为其中两个样本,样本1的图像尺寸是80×100,样本2的图像尺寸是70×100。实验中,通过手动标注图像中的河流区域,然后遍历图像中所有大小为11×11的窗口,凡窗口中心是河流像素的这个窗口被选为正样本,否则为负样本,总共获得11 700个图像窗口,其中正样本窗口有1361个,最后从这些图像窗口提取PLFT特征并训练一个LMNN分类器。

图4 实验样本图像
为了进行比较,运用文献[6]中所提的LFT特征进行同样分析步骤的比较实验。经过对这50幅卫星实验样本图像的分析,获得这两类特征分类性能的实验结果见表1,可以发现这两类特征均能较为准确地将卫星图像的背景分离开来,故而其平均分类正确率都较高,但是PLFT对于河流分类的正确率则明显高于LFT,表明该特征更适用于本课题。
3.2 本文方法检测效果
验证本文方法的检测效果,从Google Maps中选取100张具有不同地貌地形的卫星河流图像,图5(a)所示为其中的4张具有代表性的图像。实验中,运用有监督的PLFT特征及LMNN分类算法依次提取这4张图像的河流信息,其分类结果如图5(b)所示;然后运用无监督的k-means聚类算法依次提取图像河流信息,其分割结果如图5(c)所示。可以发现,基于PLFT和LMNN的方法能够将图像中的绝大多数背景干扰信息去除,但对有用的河流信息破坏也较大;k-means聚类的方法能更完整地保留河流信息,但其却难以去除背景干扰信息。
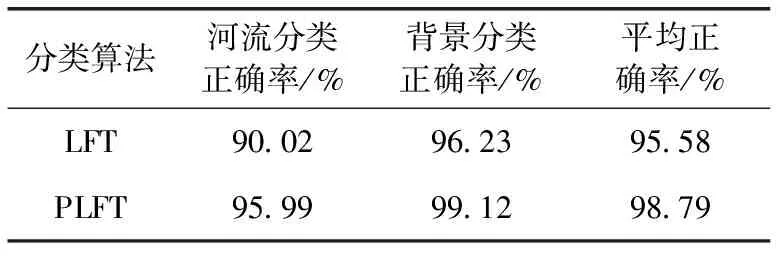
表1 PLFT和LFT分类性能的比较
经上述分析,接下来将以上两种方法的结果进行融合。首先对图5(c)中的目标(黑色像素区域)进行标号,然后遍历每个目标,在它的区域范围内统计图5(b)中有多少个对应的黑色像素点,最后返回这个数量最大的目标,那么该目标就被认为是图像中的河流区域,这4张图像融合识别的结果如图5(d)所示。实验结果表明,本文提出的融合算法吸取了上述两种方法各自的优点,同时也摒弃了其缺点,能够有效地将卫星河流图像中的背景干扰信息去除掉,同时也能较为清晰完整地保留图像中的有效河流信息,基本能满足自动提取检测并保证一定精度的要求。
4 结束语
卫星图像中的河流自动检测在水资源监测评估、洪水预测及水污染检测中具有重要的应用价值。本文提出了一种新的局部图像描述算子,即基于主元分析的局部傅立叶变换特征PLFT,用来提取卫星图像中的河流信息,实验结果表明,该特征较传统的LFT算子有更好的分类鉴别能力。其次,本文将基于PLFT特征和LMNN分类器的有监督学习分类算法和基于k均值聚类的无监督聚类分割的算法进行融合,来用于卫星图像中河流的识别。选取大量Google Maps卫星图像进行实验,结果表明提出的方法更加清晰完整地检测出卫星图像中的河流信息,具有较高的实用价值。今后的研究中,可以尝试使用核密度估计[11]的方法对彩色卫星图像进行分割。

图5 不同方法实验结果对比
