Spark平台下关联规则算法的优化实现

梁瑷云，袁 丁，严 清，刘小久

(四川师范大学 计算机科学学院，四川 成都 610101)

0 引 言

关联规则算法是数据挖掘算法中的一个经典算法，其目的在于从海量的、价值密度低的数据中挖掘出潜在的、高价值的关联关系[1]，用以辅助用户获取有效信息。传统的Apriori算法设计简单、结构清晰、易于实现，尽管如此，该算法仍然有值得优化的地方：①大量临时形成的无效项集引发内存溢出；②多次访问数据库引发系统I/O负荷失衡，甚至系统宕机；③采用单机环境实现，执行效率低、花耗时间长、实效性低。值得注意的是，现有的单机串行的算法运行模式已经无法满足当前大数据时代背景下的需求。此时，MapReduce分布式并行处理框架的出现，正好为关联规则算法的研究提供了新的思路和研究方向。本文主要针对关联规则算法所存在的无效候选集多、单机运行时间短等问题，提出基于Spark平台的Apriori并行优化算法(本文简称Apriori_MC_SP算法)，利用矩阵结构，压缩事务数据库的存储空间，减少了算法的扫描次数；同时利用矩阵存储频繁k项集，采用分组模式，直接生成局部频繁k项集，简化了频繁k+1项集的生成过程；利用Spark分布式计算框架实现并行化处理，增加系统的可扩展性，提高了算法的执行效率。

1 相关工作

随着大数据分析技术发展越来越成熟，研究学者们开始尝试将关联规则算法与并行化技术相结合，针对已有的并行Apriori算法所存在的问题，提出了一系列的解决方案。

在国外，文献[2]用MapReduce思想提出了一种的Apriori并行化算法，该算法伸缩性较好，但索引能力较差，仅适合处理小量的结构化数据集。文献[3]提出一种有效的关联规则算法——ScadiBino，将离散化的数据集转换为二进制编码，通过执行多个Map操作和执行一个Reduce操作，实现算法的并行化处理，提高算法的运行效率。文献[4]提出一种基于Spark平台的关联规则算法YAFIM，该算法引入HashTree概念，对候选集存储进行优化，节省存储空间，提高算法的运算效率。

在国内，Guo Fangfang等[5]利用水平分割的思想，提出一种基于多叉树的并行Apriori算法，该算法利用多叉树生成候选项集，有效减少了中间节点产生候选项集的数量，降低了数据库的访问次数以及各节点间的通信次数，有效地节省了数据存储的空间。Wang Qing等[6]针对在Hadoop平台下MapReduce模型处理节点失效、基于磁盘读取数据缓慢等缺陷，将优化后的Ariori算法移植到Spark平台进行实现，该优化方法在一定程度上节省了内存存储空间，但在Map过程中产生的大量中间节点存储在内存中，造成资源浪费。Yan Mengjie等[7]基于Spark平台提出一种改进算法——IABS算法，对事务数据库的转化过程和候选集产生过程进行优化，并与文献[4]中提出的YAFIM算法进行比较，该优化算法的性能明显提高。Niu Hailing等[8]提出一种AMRDD算法，利用Spark平台基于内存计算的优势，运用局部剪枝和全局剪枝策略，缩减生成候选项集的数量，但该算法仍然没有解决产生大量无效候选集的问题。Xie Zhiming等[9]基于Hadoop平台利用MapReduce框架提出一种Apriori_MMR算法，该算法结合数据划分的思想，利用矩阵的特性，简化候选项集的生成过程，从而提高算法的性能。

2 基于Spark的Apriori算法的优化改进

2.1 关联规则算法的相关概念

本文采用部分符号标识及其相关定义见表1。

本文对关联规则算法进行优化，引入了矩阵的概念，其相关定义如下：

定义1 事务布尔矩阵B，矩阵的行表示事务数据集D中的记录，列表示所有数据集中项的集合[15]，其形式如式(1)所示

(1)

表1 部分数学表达式定义

定义2 某频繁k项集{Ii,Ij,…,Ip} 的内积运算方式，详细定义参见文献[15]，如式(2)所示

(2)

其中，(Ii,Ij,…,Im)⊆I,B(Ii)表示布尔矩阵中的某Ii列的数据。

定义3 某1项集{Ii}的支持度计数[14]sup_count满足如式(3)所示

(3)

定义4 某多项集{Ii,Ij,…,Ip}支持度计数的求和运算如式(4)所示

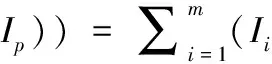
(4)

定义5 支持度sup，即项集Ii在整个数据库中所得比例，详细定义见参见文献[15]，计算方式如式(5)所示

sup(Ii)=sup_count(Ii)/counts(D)

(5)

其中，counts(D)表示数据库D的总事务数。

2.2 传统Apriori算法简介

Apriori算法主要采用简单的迭代技术，利用已知的频繁k项集“自连接”生成候选k+1项集，通过逐层搜索统计候选k项集出现的次数对候选项集进行“剪枝”。其具体实现流程见表2。

表2 传统Apriori算法的实现流程

从表2中可以看出，传统的Apriori算法不仅会多次扫描初始数据库，而且在频繁k-1项集“连接”过程中会形成大批无用的候选k项集，占用内存空间，拖慢执行进度。为适应当前大数据时代背景，设计高效的算法优化方案是非常必要的。

2.3 Apriori优化算法描述

本文所提出的Apriori优化算法利用“分治”思想，将大型数据库切割成多个均匀的数据块，针对各个数据块转化为布尔矩阵。该算法主要对频繁k(k=2)项集生成频繁k+1项集的过程进行优化。算法具体实现流程如下：

步骤1 扫描事务数据库D，对数据库中的数据进行均匀分块，分割成n个相同大小的数据块。

步骤2 当k==1时，将n个数据块转化为n个不同的事务布尔矩阵Bi，形如式(1)所示，生成局部频繁1项集l_fi1，返回n个数据(Bi,l_fi1),i取值为1,2,3…,n。

在对数据块进行转化为布尔矩阵时，需注意，当生成局部布尔矩阵Bi，对矩阵进行简约化处理，即判断矩阵的每行、列是否均满足所给条件(行的求和结果不小于k，列的求和结果不小于局部支持度计数)，满足则保留，不满足则删除,如图1所示。

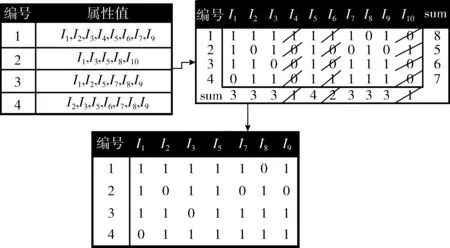
图1 事务布尔矩阵生成过程

步骤3 当k==2时，连接局部频繁1项集，直接生成局部频繁项集l_fi2，采用矩阵进行存储，结果返回(Mi2,l_fi2)。

对频繁1项集中的各项进行自连接生成2项集的过程中，运用式(2)、式(3)计算某2项集的计数是否不小于局部支持度计数，满足条件，则将该项集保存到二维矩阵l_fi2中，最后将l_fi2扩展为1维数组，去重后对分块矩阵进行行列筛选，形成新的矩阵。

步骤4 当k>2时，首先将频繁k-1项集进行排序后按照前k-2项进行划分，并采用前k-2项属性值作为块标号；其次采用下述连接方法，利用式(2)、式(4)形成频繁k项集，避免无效项集的产生，占用资源，返回(Mik,l_fik)。对该步骤进行迭代，直至满足条件k，或出现频繁项集为空时返回k-1时的结果值。

自连接方式主要为两种：块内自连接、块间自连接。

(1)块内自连接：当块内项集的个数不小于1时，采用该连接方式执行，如图2所示，以标号为“I2”的块进行解析，(I2,I5)， (I2,I7)连接生成(I2,I5,I7)，采用式(2)、式(3)运算其支持度计数；满足条件，则添加到频繁k项集矩阵中。

(2)块间自连接：当总块数不小于1时，采用该连接方式执行，图2中以(I2,I5)为例(此处k=3)，采用后1个项作为查找依据，即“I5”去查找对应的分块标号，然后连接生成(I2,I5,I7)、 (I2,I5,I8)两个项集，在进行自连接的同时，需判断该项集是否存在于l_fck中，若不存在，则需对矩阵中的相应列进行相关运算，运算结果满足条件则保留至二维矩阵l_fck中。如图3所示，当k=4时，划分频繁3项集后，应采用前两项作为块表示，后两项作为连接依据。

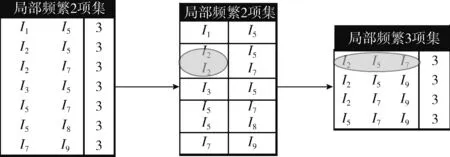
图2 生成局部频繁3项集

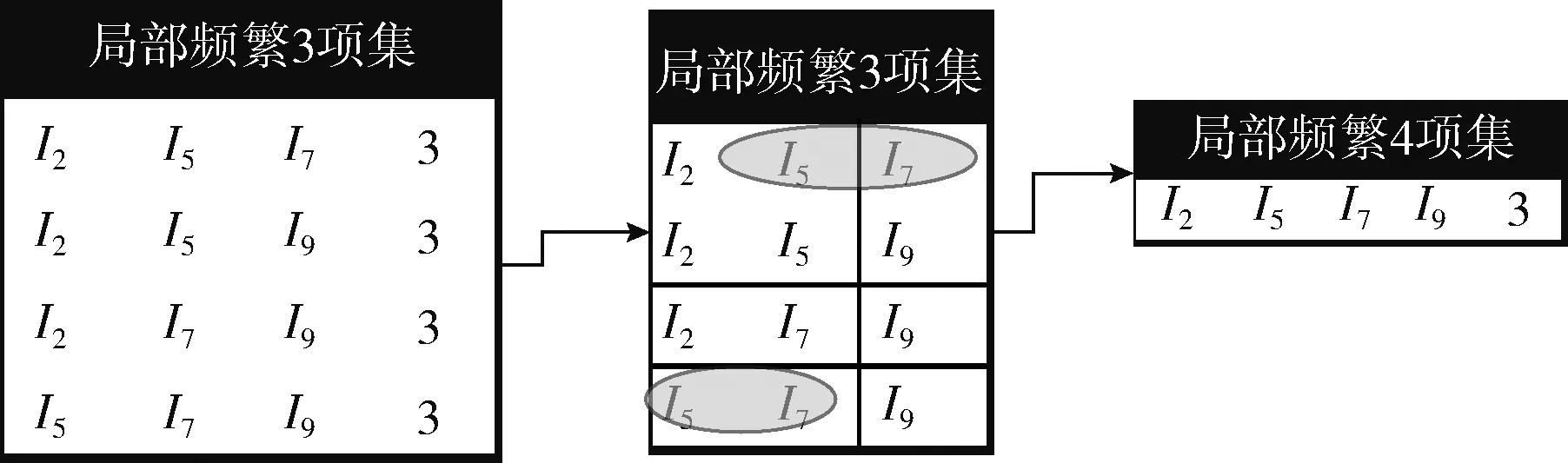
图3 局部频繁4项集的形成过程

步骤5 根据相同的“健”(即局部频繁项集)进行“值”(即局部频繁项集的求和结果)相加，合并所有分块的局部频繁项集，生成全局候选频繁项集fk，再根据最小支持度计数，进行全局剪枝。

2.4 Spark平台下的Apriori_MC算法基本思想

Spark框架是专为大规模数据处理所设计的通用并行框架，引入弹性分布式数据集[10](resilient distributed dataset，RDD)概念，RDD是一个具有容错性的数据集合，该数据被分成多个分片，存储在集群的各个节点的内存中，当内存容量不够时，这些数据会自动写入磁盘。RDD具有两种类型的操作模式：transformation(转换)和action(动作)，前者的主要目的是从现有的RDD数据对象中重新创建或重新计算，从而获得一个新的RDD数据对象，例如map()、flatMap()、filter()、distinct()、groupByKey()等。这些转换操作具有惰性，即在对RDD进行转换操作时，该操作并不会立即执行，仅仅记住这些操作；后者则通过某种特定的方法将多个RDD对象进行合并，生成一个最终结果，如count()、collect()、foreach()、reduce()等函数。在程序执行过程中，当RDD调用Action函数时，才会执行相关的Transformation函数进行计算。

Spark系统以MapReduce框架为核心，主要针对Hadoop存在的问题而设计的一套框架[11]，具有使用简单、自动容错、负载均衡、扩展性强、可靠性高等特点[1]，相较于Hadoop框架，它主要有以下优势：

(1)Spark实时性强，擅长处理流数据，而Hadoop则擅长处理批量数据。当随机访问数据时，Hadoop执行效率明显低于Spark。

(2)Spark最大的优势在于面向内存进行计算[12]。Hadoop平台面向磁盘存储数据，在调用数据时，Hadoop需要先将数据从磁盘中调入内存进行运算，而Spark直接在内存中进行计算，无需进行磁盘I/O操作，相比之下，内存处理速度明显高于磁盘速度。

(3)Spark改进了shuffle过程，提升了Spark的运行速度。Shuffle是Map阶段和Reduce阶段交流的纽带，在Hadoop平台上，shuffle过程强制要求数据按key值进行排序后分发到Reducer上，而Spark平台上的shuffle过程则是用户在有需求的情况下才会对结果数据进行排序(即调用sortBy()或sortByKey())。两者相比，Spark的设计更加合理有效。

基于以上几点，本文将改进后的Apriori_MC算法移植到Spark平台，通过执行k个Map操作以及一个Reduce操作过程，实现算法的并行化处理。在Map阶段，Spark将数据分成多个分块(分块数个数视集群情况而定)，将各个分块分别部署到不同的工作阶段中去，按照第2.3节中描述的Apriori_MC算法的执行流程进行部署实现；在Reduce阶段，将在Map阶段产生的分块结果按照键值进行求和，获得全局候选k项集；最后将通过filter()函数对全局候选项集进行筛选过滤，从而获得全局频繁k项集。整个算法的流程如图4所示。

Apriori_MC_SP算法核心伪代码如下：

图4 Apriori_MC_SP算法执行流程

输入： 存储路径path， 最小支持度min_sup， 所求频繁项集数k， 分块数n

输出： 频繁k项集fk

(1)某事务数据库被存储在path路径下的文件中， Master工作节点利用textfile()读取文件， 读取后创建一个新的RDD， 该RDD中的数据包含n个数据块。

rdd←sc.textfile(path, n)

(2)Map阶段：

for t←1 to k do:

if t==1 then :

rdd← rdd. mapPartitions( fc1(split, min_sup, k))

if t==2 then :

rdd← rdd.map( fc2(split, min_sup, k))

if t>2then :

rdd←rdd.map( fcn(split, min_sup, k))

(3)Reduce阶段：

fk←rdd.flatMap(_).reduceByKey(_+_).filter(_>= min_sup_count)

上述过程中主要涉及以下3个函数：

(1)函数fc1(split, min_sup, k)：

该函数目的是构造简约化布尔矩阵M1， 生成频繁1项集f1， 返回结果(M1,f1)， 相关实现如下：

begin

L1←sorted( unique ( flatten ( split) ) )

#扩展数据库为1维数组， 同时进行去重、 排序

w ← len(split) # w为分片长度

h ← len(L1) # h为L1长度

sup_count←min_sup * w

MatrixM←zero(size=(w, h) ); #构建零矩阵

for m←0 to h do :

for m←0 to w do :

if L1[m] in split[n] then :M[m, n] ←1

for m←0 to h do :

sums←sum(M[:,m]) #对矩阵每列进行求和

if sums >=sup_count then: f1.add(L1[m])

M1← Mat_process (M,f1, k)

# 调用Mat_process为筛选行/列的函数

return (M1,f1)

end

(2)函数fc2(split, min_sup, k)：

该函数的目的在于生成频繁2项集， 返回结果(M2,f2)， 相关描述如下：

begin

f2,f1,M← [], split [1], split [0]

for m←0 to len(f1)-1 do :

for n←m+1 to len(f1) do:

sums←sum(M[:,m]&M[:,n] )

l←[ [f1[m] ,f1[n]] , sums] #二维数组

if sums>=sup_count and l not inf2then:

f2.add( l)

M←Mat_process(M,f2, k)

return (M,f2)

end

(3)函数fcn(split, min_sup, k)：

该函数主要针对当k>2时， 采用块内自连接和块间自连接两种方式， 返回结果(Mn,fn)， 相关描述如下：

begin

f,M, result ,fn←split [1][:,0], split [0], 1, []

gid=unique(f[:,0:k-2]) #对二维矩阵进行分块标记

for each id in gid do :

group← select(f2[:,0:k-2]=id)

for each i←0 to len(gid)-1 do:

#块内连接

for each p←i+1 to len(group) do:

l←sorted(group[i,:] ∪group[p,:])

for u in A:result*=M[:,u]

if sums(result)>sup_count then :

fn.add( [l, sums(result)])

#块间连接

dev ← group[i][-(k-2):]

Group←select(f2[:,0:k-2]= dev)

for ecah item in Group do:

l← sorted( group[i,:]∪item )

for u in l: result*=M[u]

sums←sum(result)

if(sums>= sup_count) and [l,sums] not infn:

fn.add([l, sums(result) ])

M← Mat_process (M,fn,k)

return (M,fn)

end

2.5 时间复杂度

假设在Spark平台上单个分块的事务数为D,其中事物项集的数量为M，共N个这样的分片。

在单个分片中，采用传统的Apriori算法，扫描一次数据库以及获得频繁1项集的耗时O(MD)，在频繁k-1项集生成候选k项集的“自连接”过程中，所需耗时O(Lk-1*(Lk-1-1)),“剪枝”生成频繁k项集所需耗时O(Ck)。遍历整个数据库计算候选频繁项集Ck所需耗时O(Ck*D)，传统的Apriori算法平均情况下，所需的时间复杂度为

(6)

对Apriori_MC算法来说，当k==1时，其转换矩阵以及生成频繁1项集所耗时O(MD)；当k==2时，“自连接”步骤直接生成频繁k项集所耗时O(Lk-1*(Lk-1-1))；当k>=3时，对频繁二项集进行分组操作，在最坏的情况下，其时间复杂度为O(Lk-1*(Lk-1-1))，则该算法在最坏的情况下所需的时间复杂度为

(7)

对比式(6)与式(7)，明显传统Apriori算法的时间复杂度高于Apriori_MC算法的时间复杂度。其原因是Apriori_MC算法扫描数据库操作仅进行一次，忽略了局部“剪枝”过程，减少中间结果的产生，释放部分内存，缩短了算法的时间复杂度。

3 实验分析

3.1 实验数据

本实验部分将采用两种数据集进行实验测试，数据集特征见表3。

(1)数据来源于频繁项集挖掘数据集知识库[13]的数据集：Connect。

(2)数据有IBM数据生成器随机生成数据。

表3 数据集特征

3.2 实验环境

本文采用的实验环境：6台CPU Inter Core4、4G内存、1T、磁盘ubuntu14.04的操作系统的台式计算机，每台计算机通过交换机构建小型局域网，并利用操作系统提供的SSH服务进行免密通信。在搭建Spark Standalone集群的过程中，需要JDK1.8、Scala2.10、Hadoop2.6以及Spark1.6等软件包的支持，本文实验主要采用Python3.5进行实现，其依赖Pyspark、Numpy等库文件。

3.3 实验结果分析

本文实验部分将采用3种不同的Apriori方案进行验证：传统的Apriori算法、来自文献[14]的优化方案、以及前文设计的Apriori_MC方案，将这3种方案移植到Spark平台部署实现，分别命名为：Apriori_SP、MApriori_SP、以及Apriori_MC_SP算法。

实验1：支持度阈值的设定对算法的影响

支持度阈值的设置对关联规则算法的执行速度和频繁项集的数量会带来一定的影响。若支持度阈值设定过高，产生频繁项集数量过少，则无法更好展现算法的执行效果；若支持度阈值设置的过低，生成的频繁项集过多，容易造成集群的中间节点运行失败后再次计算，增加了集群的工作量。本实验主要目的在于验证支持度发生变化时不同方案的执行效率验证以及输出结果。该实验采用Connect数据集进行验证，输出结果要求返回频繁3项集，3种方案的执行效率见表4，频繁3项集的数据见表5。

表4 支持度变化时3种方案的性能对比

表5 支持度变化时3种方案的输出结果对比

在表4中可以得出，在数据集一直地情况下，随着支持度的减小，3种方案的执行时间随之增加。在表4中，传统Apriori算法的执行时间最长，运行效率最低。将MApriori_SP与Apriori_MC_SP方案进行对比，当支持度sup>=0.4时，两种方案的执行时间相差不大；当sup<0.4时，Apriori_MC_SP算法的运行效率明显优于MApriori_SP方案。

从表5中可以得出，随着支持度的降低，频繁项集的数量也相应增加；同时，本文提出的Apriori_MC_SP方案与传统的Apriori算法的频繁项集在数量上保持一致。

因此，支持度的选择是影响关联规则算法执行效率的一个重要因素。

实验2：不同数据集下算法的执行效率对比实验

本实验将采用100万条的随机数据集中分别提取20万、40万、60万、80万以及100万条数据集进行测试，由于该数据集的事务数量过大，为避免结果产生的频繁项集过少的情况，将最小支持度阈值设置为0.1，挖掘频繁3项集，在数据集量不同的情况下，3种方案的执行效果如图5所示。

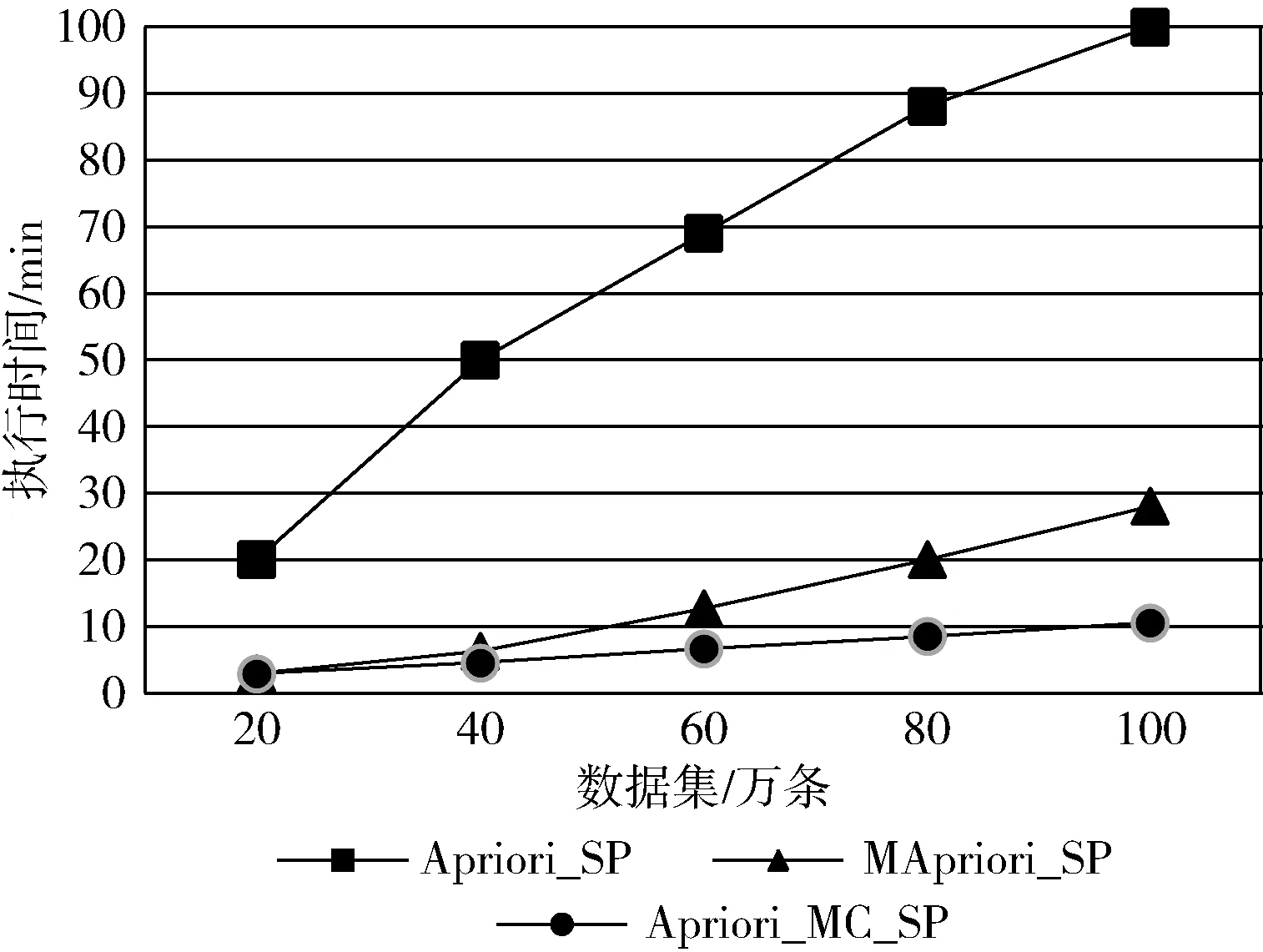
图5 不同数据规模下3种方案的性能对比

在图5中可以得出，随着事务数据集的规模逐步扩大，算法的执行时间也随之增长，同时也反映出传统Apriori算法比其它两种方案的执行时间长，并不满足当前大数据时代对数据分析的要求。当数据集的数据量小于40万时，Apriori_MC_SP与MApriori_SP方案的执行时间相差较小，但当数据量越来越小时，Apriori_MC_SP方案的执行效率则快于MApriori_SP算法。

实验3：Spark集群的工作节点数对算法的影响

该实验的目的是验证集群的工作节点是否影响算法的运行效率。该实验选取随机生成的60万条数据作为验证对象，最小支持度阈值设置为0.1，分别验证不同工作节点下Apriori_MP_SP方案的执行状况，实验结果如图6所示。

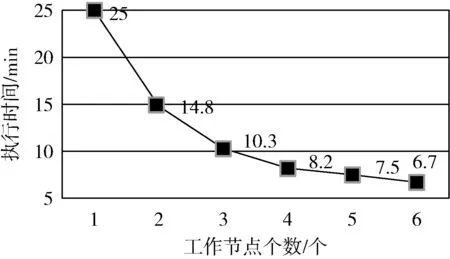
图6 不同工作节点下的执行效率

从图6中可以得出，在数据集不变的情况下，工作节点增加，集群可使用的内存资源加大，使得集群处理大数据量的能力加强，从而加快了算法的执行时间。图中，当工作节点数大于等于3时，执行效率下降的速度明显减缓。

综上所述，支持度的设定、数据规模、Spark集群规模均会影响算法的执行效率。本文提出Apriori_MC_SP方案在保证输出结果与传统Apriori算法一致地情况下，在很大程度上提升了关联规则算法的执行效率，且该算法更适用于大数据量的关联规则提取。

4 结束语

本文提出的Apriori_MC算法，运用分治思想，基于Spark集群框架，实现了关联规则算法的并行化计算，有效解决了数据库扫描次数多、系统I/O负载量大、无效的中间局部频繁项集多等问题，提高了关联规则算法的运行效率。当然，在算法的实现过程中仍然存在一些缺陷，在实验过程中，随着数据量的增长，算法产生的中间结果越多，在采用Spark集群进行测试的过程中，未充分考虑实验过程中数据倾斜所带来的问题，造成各工作节点运行时间不稳定的现象。后期将着重对这些问题进行深层次的研究，以期获得更理想的效果。