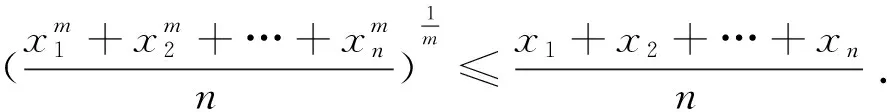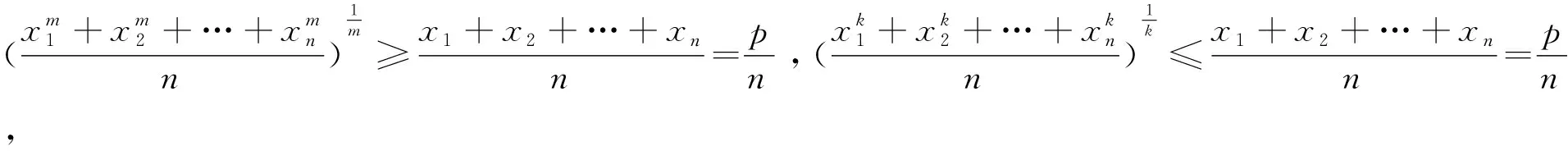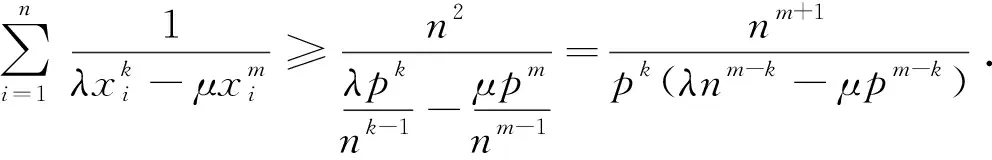数学探究应该怎么“做”？——以一道自主招生题的多种解法与拓展为例

温州大学数理与电子信息工程学院 (邮编：325035)

在数学的领域里重要的不是你知道什么,而是你是怎样知道的,数学课上教学生怎样思考比思考什么更重要.数学教学要注重引导学生经历知识的探究过程和学会数学探究的方法,数学教学应该被看作是教师与学生对有关知识领域的探究.数学学习最重要的应该是对数学问题的深入探索,并学会如何运用学科思维的方式进行思考.数学教学的最终目标是帮助学生发展与当代正活跃的数学家相一致的理解方式和思维方式,学生应该及早地像数学大师那样去追求和进行大量的创造性思考活动,而不要被学校里那种无休止的练习弄得头脑僵化和困乏,那实际上是沉溺在无益的练习之中.[1]学习数学的重要方法是自己动手做数学,只有在“做数学”的过程中,数学的探索性才能得到展现,学生的创造性才能得到发展,学生才能真正学会“数学地思维”,才能使得数学跳出枯燥、乏味的笼牢,彰显数学思想方法的深邃与高贵,展现数学所独有的精神和魅力,发现数学创造的真谛,体会到数学创造的乐趣和数学美.

笔者在文[2]中论述了数学探究的教育价值,并从学科底蕴角度论述了数学探究教学的必要性.在文[3]中提出数学教学中应加强问题的变式、引申与推广以培养学生的探索能力.在文[4]中又进一步指出:为了更好地培养学生“发现”和“提出”问题的能力,教师要主动地让不同层次的学生都能以探索者的姿态出现,在探究中发现新颖而独特的解决方案,问题的解决带来成功的体验,从而激励学生再发现和再创新.然而,在教学实践中,许多教师由于数学素养和能力不足,常常不知如何进行数学探究?迫切希望有一种模式或方法来有效指导组织数学探究活动.笔者在文[5]中也给出过一个提出数学问题的模型(见图1),这个模型无疑对一线的数学教师在指导学生提出数学问题或从事数学探究时具有重要的参考价值.现以一道浙江大学自主招生问题的证明与拓展为例,通过一题多解和推广拓展,进一步给出数学探究的一个基本模型(见图2),以供从事数学探究的同行参考.

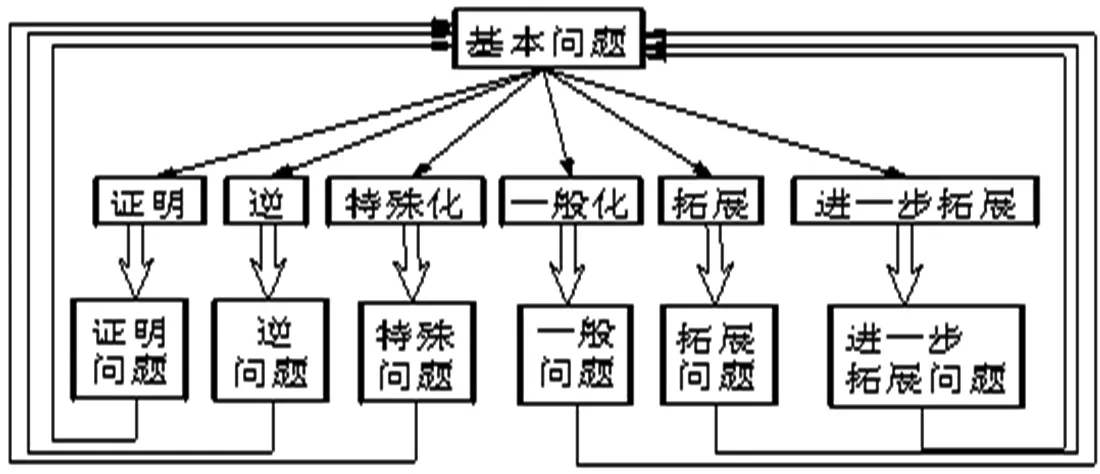
图1

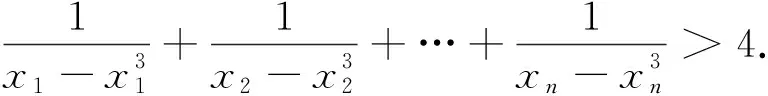
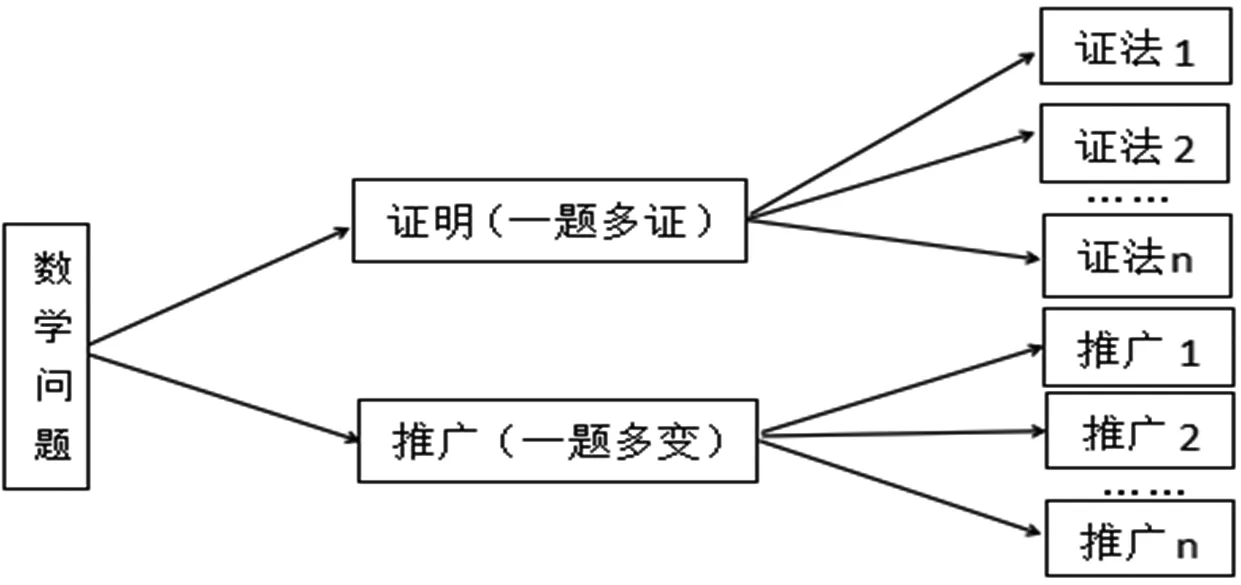
图2

先给出这个问题的三种不同证法.

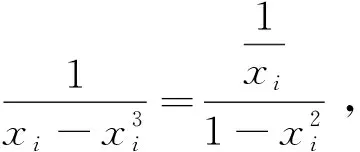
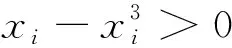
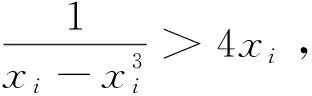
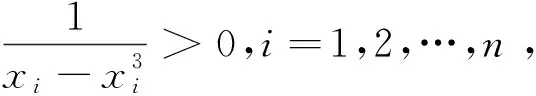
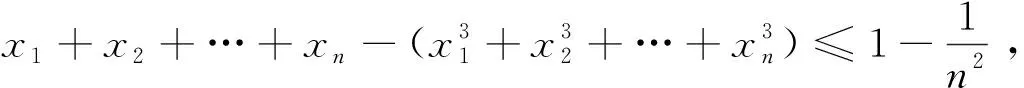
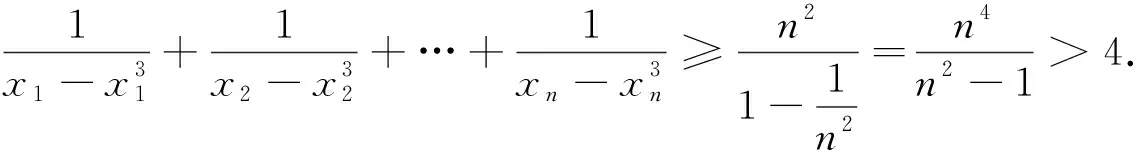
从以上可以看出,这三种证法都需要一定的技巧和灵感,出乎意料和又令人震惊,体验到数学的神奇和数学的美.实践中,数学家在解决问题时也总是喜欢努力去寻求对问题的不同证法尤其是新颖简洁的证法.正如高斯曾指出:“绝对不能以为获得一个证明以后,研究便告结束,或把另外的证明当作多余的奢侈品.有时候一开始你没有得到最简和最美妙的证明,但恰恰在寻求这样的证明中才能深入到真理的奇妙联想中去,这正是吸引我去继续研究的主动力,并且最能使我们有所发现.”因此,寻求对问题的不同解法尤其是新颖简洁的解法,是数学家研究的一种基本策略,也是数学探究的一种基本形式.

而且,数学家们常常不仅仅只是喜欢证明定理,很多情况下他们更喜欢以已有的定理为基础,尽可能多地得到新的问题或结论,这是数学家的本性,也是数学探究的一种基本形式.数学教学中应突出这种超出原习题解法的探索活动,而是适当、有机地对原习题进行深层次的探索,开拓创新和触类旁通,找出一些特殊问题中所蕴含的内在的规律性,挖掘出更深刻更广泛的结论,这是数学家研究数学的共同特征,也是数学探究中所需要学会的拓展变式艺术,以下是对这个问题的推广命题及其证明.

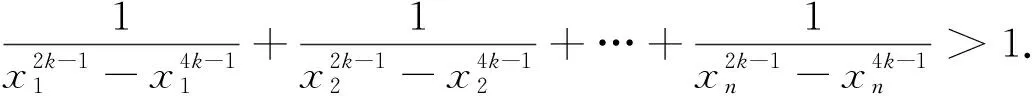
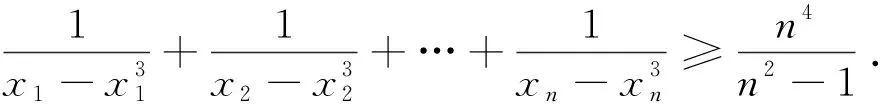
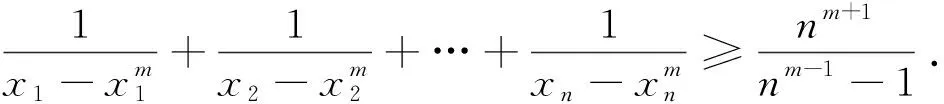
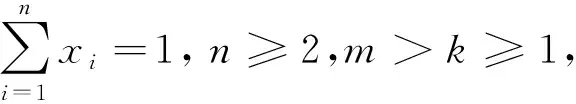
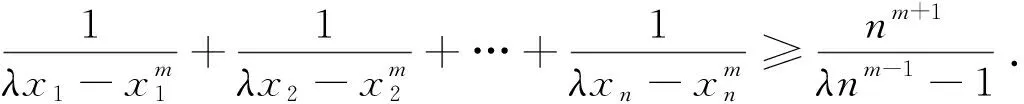
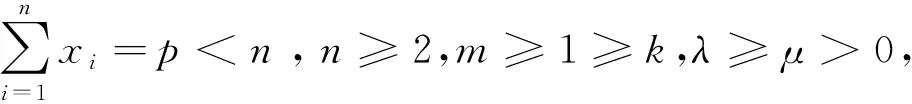
为了证明该推广7,我们先给出一个引理.

引理设xi∈R+,i=1,2,…,n,n∈N*,则: (1)当m≥1时，有

(2)当0

证明令f(x)=xm,则f″(x)=m(m-1)xm-2,

(1)当m≥1时，f″(x)≥0,由琴生不等式即得

(2)当0

推广7的证明: 因x1、x2、…、xn为小于1的正数,且m≥1≥k,λ≥μ>0,所以

由m≥1≥k和引理得

“好”的数学定理通常能够很好地和其他的数学问题触类旁通,能引发各个方面深刻的结果.实践中,数学家们从不满足于只是仅仅解决已有的问题,而总是通过推广原有的概念、理论和方法去寻求更大范围内的统一,发展和构建新的理论或提出新的数学问题.用数学家C. S. Pierce的话说:“数学思想的一个特征是当它不能推广时,它就没有成功”.[13]一旦有必要,数学家们总是力图使概念一般化(推广).数学研究工作者若能成功地推广已有的理论或方法,则其研究就推进了一步.数学能用这个方法扩大其范围,这一工作确实是无可限量的.[14]本文针对一道自主招生问题寻求到三种不同的证法,并进一步通过推广得到不同的拓展命题,促使学生学会多层次、广视角、全方位地认识、研究问题,从而培养学生的探究意识和创新能力,这是数学探究的一种基本策略和方法,许多数学家即使是从事最前沿的数学研究也是用这种方法去获得许多创造性成果的.学生学会了这样去探究数学问题,就学会了数学探究的方法,培养了数学创造的意识和能力,也可以领悟到数学研究的精髓,体会到生动活泼的数学创造.事实上,数学家们从事的前沿数学研究和初等的数学在本质上并没有什么差异,只是增加了抽象层次而已,增加抽象层次本身并不会导致更困难的数学,在每个抽象层次,做数学实际使用的方法大致上是一样的.数学教学的一个主要目标就是要培养学生数学探究性思考的能力和方法,只有这样,才能使学生形成较强的学习迁移和适应能力,才能“以不变应万变”,才能形成真正的数学学习和创造能力.

事实上,很多习题都存在着进一步扩展其数学功能的可能性.学生在做一些经过精心安排的习题的时候,他们不仅在积极地掌握数学课的内容,同时也在获得进行创造性思维的能力.这些能力表现为:善于运用某一种方法、手段而改变问题情境;善于构想新的解题手段和解题思路;善于在原有题目的基础上构想出新的题目.[15]这就要求我们平时要有意识地对所做的数学问题的由来、所用方法以及创新之处进行归纳总结和深层次思考,注意发现不同问题之间内隐的联系,以便学会发掘潜在的问题或方法,这是生长新思想、新方法和新知识的种子.同时,平时还应尽可能多地发掘具有较强探究性的“好的”数学问题,激发和调动探究意识,展现探究性思维过程,注意归纳总结数学探究的一般策略或方法.正如波利亚先生所指出:一个专心的认真备课的教师能够拿出一个有意义的、但又不太复杂的题目,去帮助学生发掘问题的各个方面,使得学生通过一道题,就好象通过一道门户,把学生引入一完整的理论领域.”[16]只有这样去组织数学探究,才能把潜在于数学中的研究精神、发现精神提炼出来使之表面化,才可以用来培养学生创见性的头脑,只有很好做到这一点的人,才称得上是真正的数学教育工作者.