基于核心素养视角下的高考试题赏析与拓展——以2018年全国卷3第16题为例

四川省成都市玉林中学 (邮编：610041) 四川省成都树德中学 (邮编：610031)

《普通高中数学课程标准(2017年版)》指出，数学学科核心素养包括6种，它们既相对独立又相互交融，是一个有机的整体．如何培养和评价学生的学科素养呢? 2018年高考试题给了我们答案：命制以检测学生素养达成情况为背景的创新型试题，主要考查学生的思维能力．下面就从一道高考题出发，来谈如何在解题中养育学生的核心素养、发展学生的能力．

1 题目与赏析

题目已知点M(-1，1)和抛物线C：y2=4x，过C的焦点且斜率为k的直线与C交于A、B两点．若∠AMB=90°，则k=__________．

视角一数学运算

数学运算指的不是四则运算而是一种思维过程，它是解决数学问题的基本手段．依据研究对象的不同，我们可以选择不同的运算思路但最终却可以得到相同的结果．在该题中根据运算对象的不同，得到了解决此问题的以下三种方法．

方法一从直线入手

本题是直线与抛物线的位置关系问题，可以通过联立直线与抛物线的标准方程，然后利用向量的数量积、借助韦达定理求解．

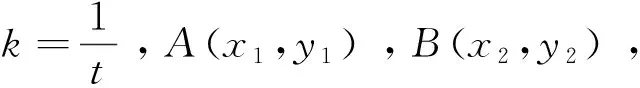
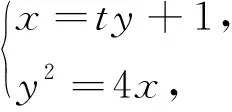
方法二从点入手

本题也可以根据抛物线标准方程的特性，用单变量表示出A、B两点的坐标，然后利用斜率公式、向量的数量积，借助整体代换的思想求解．

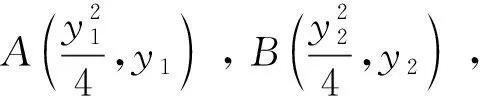
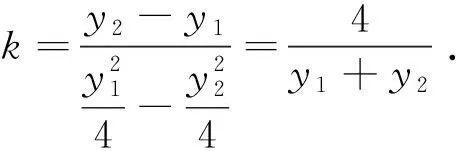
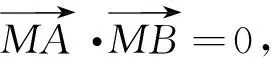
则y1+y2=2，故k=2．

方法三借助参数方程

此种方法和方法二本质是相同的．

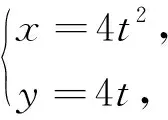
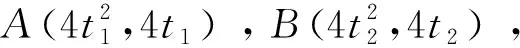
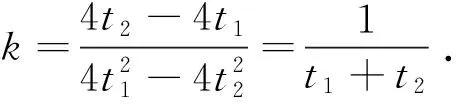
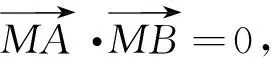
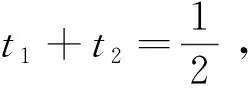
视角二直观想象

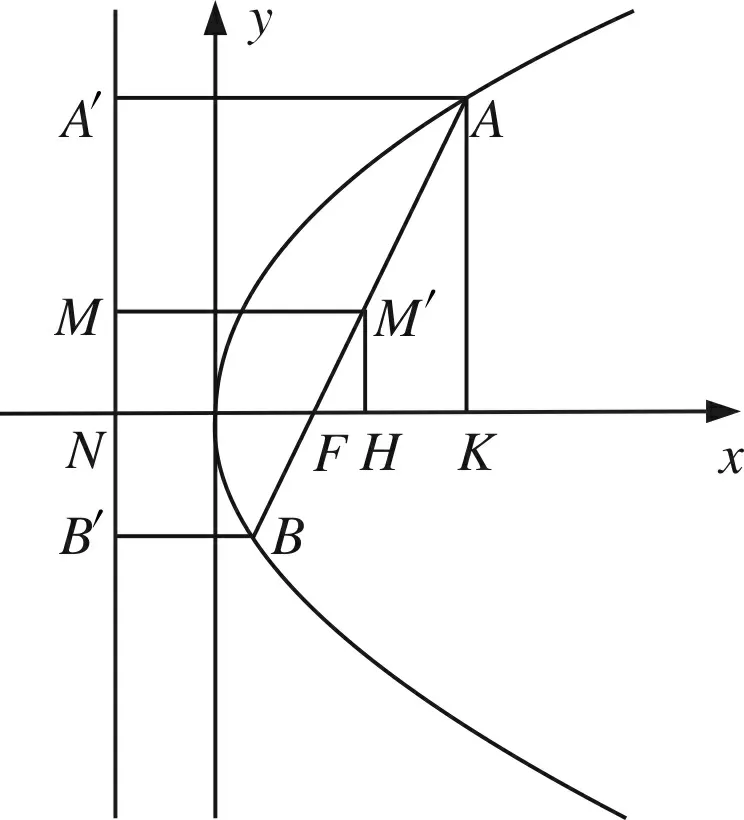
直观想象不是直观和想象的简单组合，而是二者的相互融合、相互渗透．直观想象的表现不外乎三个方面：借助图形描述问题情境，通过数形结合建立形与数的联系，基于图形理解构建数学直观．我们知道，解析几何也属于几何的范畴，自然可以采用平面几何描述代数问题，即将代数问题图形化．

本题是利用抛物线的几何定义构建几何图形描述数学问题．

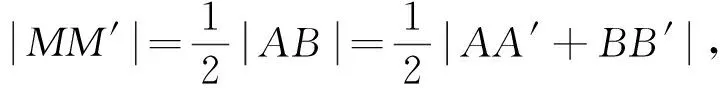
又M′为AB的中点，则MM′平行于x轴．

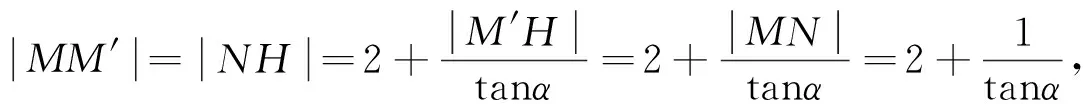
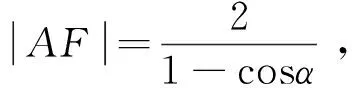
则tanα=2，即k=2．

方法五建立数形联系、凸显直观想象

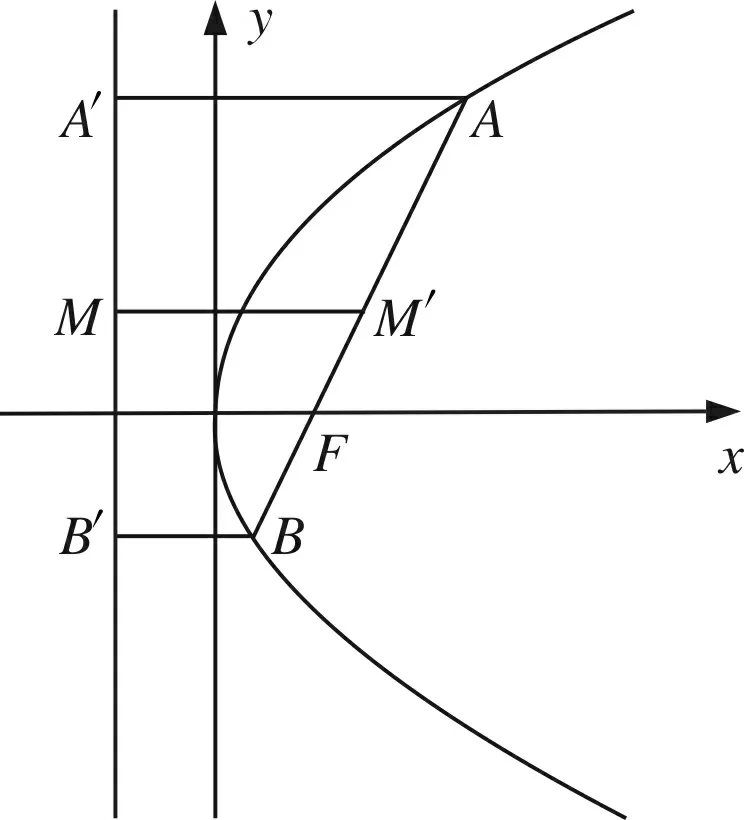
著名数学家华罗庚生动地描述了数与形的关系：“数形本是相倚依，焉能分作两边飞；数形结合百般好，隔离分家万事休．”本题中蕴含着线段成比例的几何关系(图形)，我们利用中位线分线段成比例，得到直线AB中点的纵坐标(数)，再通过点差法建立中点的纵坐标于直线斜率的关系即可．数与形的有效结合，可以最大程度上优化解题过程，提高解题效率．

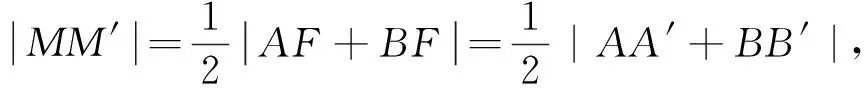
设A(x1,y1)，B(x2,y2)，故y1+y2=2.

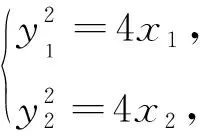
2 变式拓展

解题只是培养数学核心素养众多环节中的一环，与解题本身相比，更为重要的是反思和再创造．正如荷兰数学家弗雷登塔尔曾指出，“反思是数学思维活动的核心和动力．”下面我们立足于核心素养的视角对这道高考题进行探索、再加工．

视角三逻辑推理

文[1]中指出：逻辑推理是指从一切事实和命题出发，依据规则推出其他命题的思维过程．加里宁曾说：“数学是锻炼思维的体操．”数学思维不仅有生动活泼的探究过程，其中包括想象、类比、联想、直觉、顿悟等，而且有严谨理性的证明过程，通过数学解题培养学生的逻辑思维能力也不失为一种经济的方法．笔者利用归纳、类比推理方法得到了下面的一些命题．

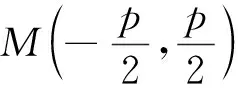
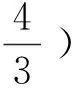
拓展4-1 已知抛物C：y2=2px(p>0)，点M在抛物线C的准线上，过点M作C的切线且切于A、B两点，证明直线AB恒过抛物线C的焦点．

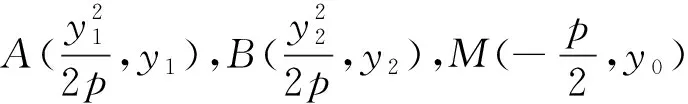
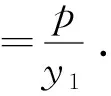
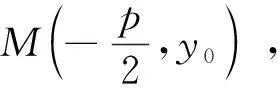
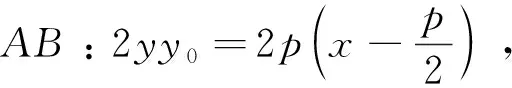
拓展4-2 已知抛物C：y2=2px(p>0)，过C的焦点的直线与C交于A、B两点，过A、B两点分别作C的切线交于点M，证明点M在抛物线C的准线上．

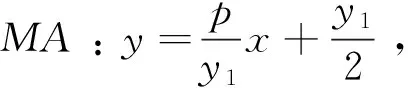
总之，数学素养的培养绝非一日之功，也不可能立竿见影，它是一种养成性教育，需要教师从长计议，从点滴做起，持之以恒，注重后发效应．在日常的教学中多尝试以下措施：

首先，注重课堂教学的多视角、知识的多模块渗透．除了解题教学外，我们应该在概念教学、问题解决教学、复习课教学等教学活动中使学生去切身体验．

其次，针对不同年龄阶段结合教学内容和案例，重视学生核心素养的培养，逐步提高学生的六大素养能力．比如直观素养的培养要加强学生对三种语言的理解与转化，多看多想、想与看结合．

最后，加强教学反思，不断提高自身专业素养，以身示范，育人才是素养的风向标．