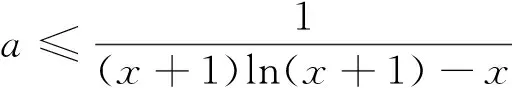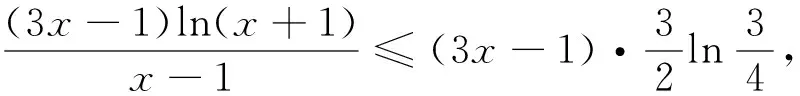顺应命题意图 提升解题效能

安徽省霍邱县第一中学 (邮编：237400)

高考数学试题的命制经历了知识立意→能力立意→素养立意的三大变革，万变不离其宗，每一道试题都是由条件和结论构成，利用条件及高中数学所学一定能得出结论.我们只有顺应命题意图，加之丰厚的高中数学所学，才能提升解题效能. 兹举数例，供读者参考.

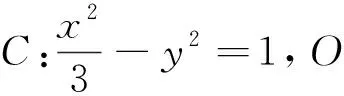
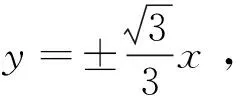
点评顺应命题意图，合理利用平面几何图形的有关性质解题，彰显数形结合思想的真谛，值得回味.

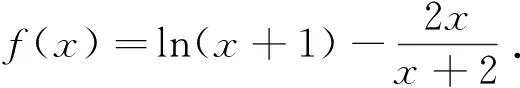
(1)证明：当x>0时，f(x)>0；

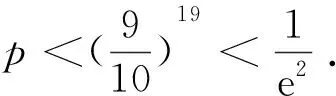
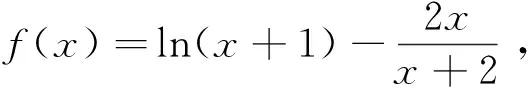
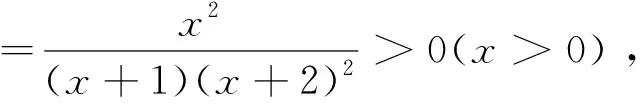
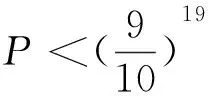
例3 函数f(x)、g(x)的定义域都是D，直线x=x0(x0∈D)，与y=f(x),y=g(x)的图象分别交于A、B两点，若|AB|的值是不等于0的常数，则称曲线y=f(x),y=g(x)为“平行曲线”，设f(x)=ex-alnx+c(a>0,c≠0)，且y=f(x),y=g(x)为区间(0,+∞)的“平行曲线”，g(1)=e,g(x)在区间(2,3)上的零点唯一，求实数a的取值范围.

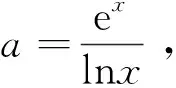
点评新定义题更彰显顺应命题意图的解题魅力，利用新定义将函数g(x)的图象转化为由函数f(x)的图象经过上下平移得到的是破解此题的神来之笔，加之娴熟的导数知识及数形结合的思想方法而快速破解，让人心花怒放，享受快乐.

点评旋转构圆，利用圆与函数的图象之间的区别与联系破解，深化对函数概念的理解，很值得我们关注.

巩固练习

1.已知an=log(n+1)(n+2)(n∈N*)，我们把使a1a2…an为整数的数n叫作“优数”，求在区间(1,2018)内的所有优数的和.

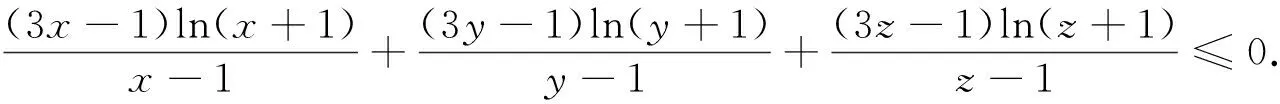
答案

1.a1a2…an=log23×log34×…×log(n+1)(n+2)=log2(n+2)，令log2(n+2)=t,t∈Z，则n=2t-2，由1<2t-2<2018，得2≤t≤10,t∈Z，所以在区间(1,2018)内的所有优数的和为22-2+23-2+…+210-2=2026.