只道寻常窗前月 更生月色水天长——一道调考试题求解引发的解题感悟

湖北省武汉市黄陂区第一中学盘龙校区 (邮编：430312)

哈尔莫斯说：数学的真正部分应该是问题和解，解题才是数学的心脏.波利亚说：掌握数学就意味着解题.罗增儒教授说：数学学习中发生数学的地方都无一例外地充满着数学解题活动.由此可见，数学解题在数学学习中极其重要.解析几何是学生高中阶段较难驾驭的一个知识板块，不少学生习惯于大题量快节奏的刷题模式来突破这一难点，收效甚微，在多年的解题教学中笔者深刻地体会到，面对解析几何的压轴试题，要想做到得心应手，平常的学习需要学生具备扎实的基本功、熟练的技巧、灵活的思路、开阔的视野和深入的钻研精神.下面就通过一道解析几何试题的求解来展示这一点.

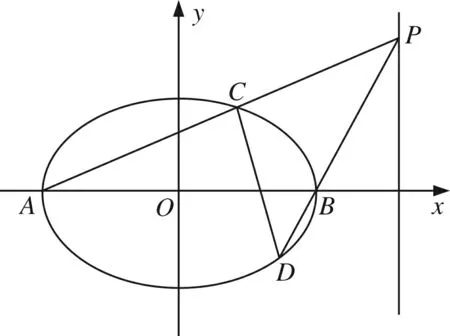
图1

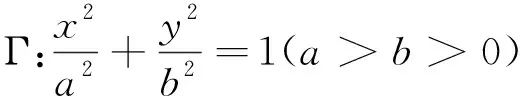
(1)求椭圆Γ的方程；

(2)若点P(x0,y0)(y0≠0)为直线x=4上任意一点，PA、PB交椭圆Γ于C、D两点，则直线CD是否过定点，若是求出该定点坐标，不是，说明理由.

这是武汉市2018届高三二月调考文科第21题，题目简洁明了，考查了椭圆方程的求法、直线与椭圆的位置关系、解方程组、韦达定理的应用，整体代入等多个知识点.重点考查运算求解能力，在思想方法上主要考查学生数形结合、转化化归的思想.

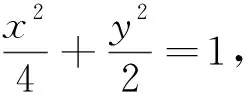
1 解题需要扎实的基本功

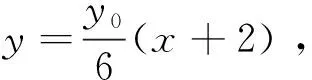
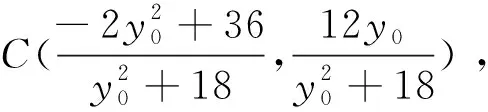
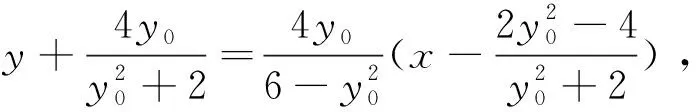
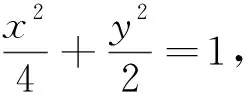
于是直线CD的斜率为

于是直线CD的方程为：

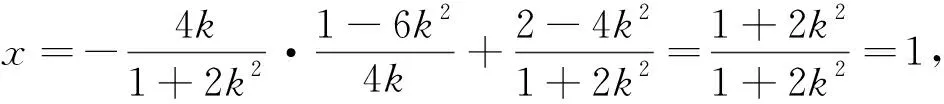
点评几何中的定点问题本质上是代数中的恒成立问题，合理选择参变量尤为重要，解法1和解法2分别选取P点坐标和直线AC的斜率作为变量，是通法，解答过程中需要两次将直线代入椭圆方程联立求解，计算量大，短时间完成需要学生有扎实的计算运算求解能力，平时必须训练有素才行.

2 解题需要熟练的技巧

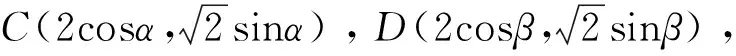
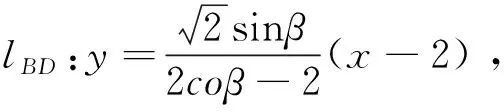
直线CD的方程为

令y=0得

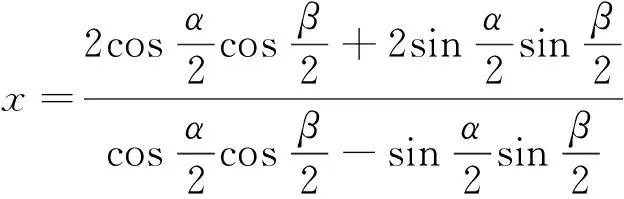
点评解法3利用参数方程，求解过程经历了用二倍角公式缩倍、化弦为切、和差化积、两角和与差的余弦展开等常见变形技巧，在准确记忆公式的基础上，对变形的熟练性上提出了较高的要求.

3 解题需要灵活的思路

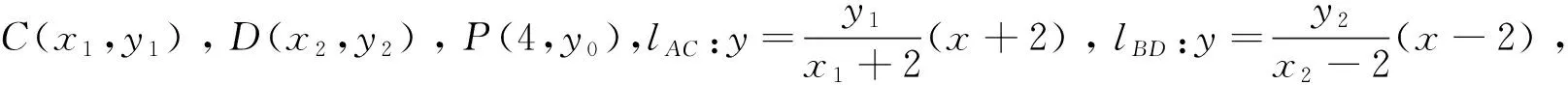
①

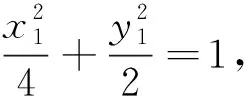
整理得：5(x1+x2)-2x1x2-8=0

②

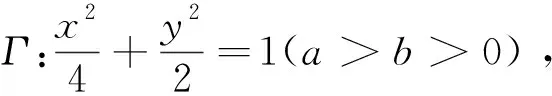
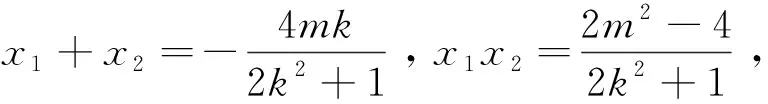
即m=-k或m=-4k.

若m=-4k，则直线CD的方程y=kx+m即为y=kx-4k，直线CD过点(4,0)，舍去；

若m=-k，则直线CD的方程y=kx+m即为y=kx-k，直线CD过点(1,0).

点评解法4基于整体思想，借助方程消参，将设而不求的思想灵活地展现出来，体现了灵活的解题思路.

4 解题需要开阔的视野

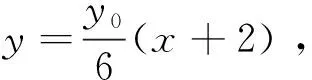
点评解法5，从曲线系发出，解答计算量很小，要求学生有较宽的数学视野，尤其具备一定的竞赛经历.

5 解题需要深入的钻研精神

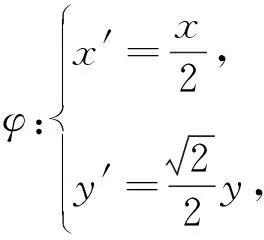
点评解法6，立足伸缩变换，找到了问题的源头，计算量很小，揭示了题目的深刻背景，需要学生平常养成刻苦钻研的良好习惯.

总之，面对难题，首先，必须树立信心，因为有了信心才能在挫折面前拥有坚持到底的勇气；其次，养成良好的学习习惯，如审题需要慢下来，谋定而后动，通过细心审视题目条件，合理选择转化途径；最后，选择科学的学习方法，比如通过一题多解，培养思维的灵活性，通过一题多探，培养思维的深刻性，并学会在不同方法的比较中学会选择，透视问题本质，优化数学思维，提升数学素养.