双绝对值问题的新认识
2018-12-22
浙江省绍兴市鲁迅中学 (邮编:312030) 浙江省杭州市第十四中学 (邮编:312012)
1 试题呈现
(2018年8月浙江20校联考填空题压轴题第17题)如下:
设函数f(x)=|x2+a|+|x+b|(a、b∈R),当x∈[-2,2]时,记f(x)最大值为M(a,b),则M(a,b)的最小值为_________.
笔者在阅卷过程中,发现得分率几乎为零.在与学生的交流中发现,此题对学生而言,有一种既熟悉又陌生的感觉.熟悉的是题目条件又是绝对值形式,问题也是熟悉的最值嵌套问题,陌生的则是此题该如何下手,如何成功地破解题中的双绝对值呢?
2 常规解法探究
这道题主要考查的是双绝对值函数最值的求解,考验学生的阅读理解能力,转化能力,对绝对值不等式的理解与应用的能力.下面先谈谈这个试题的常规解法:
根据绝对值恒等式|m|+|n|=max{|m+n|,|m-n|,
可以将原函数写成f(x)=max{|x2+x+a+b|,|x2-x+a-b|}.
如何处理这两个绝对值呢,有以下的三种视角:
视角一利用绝对值三角不等式
解法1 由二次函数的性质可知
|x2+x+a+b|max=
同理|x2-x+a-b|max
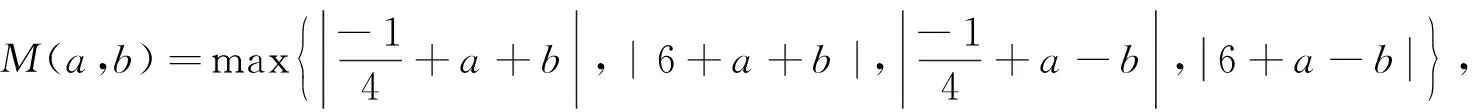
所以

视角二以形助数,利用图象处理绝对值函数值域
解法2 同前,
下面把a+b与a-b看成整体,作为变量,分别画出函数图象,如下图
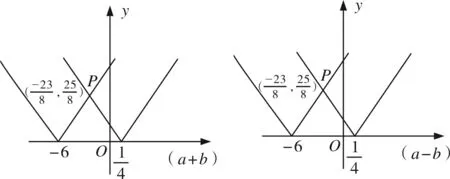
视角三利用绝对值的几何意义
解法3 因为|a|+|b|=

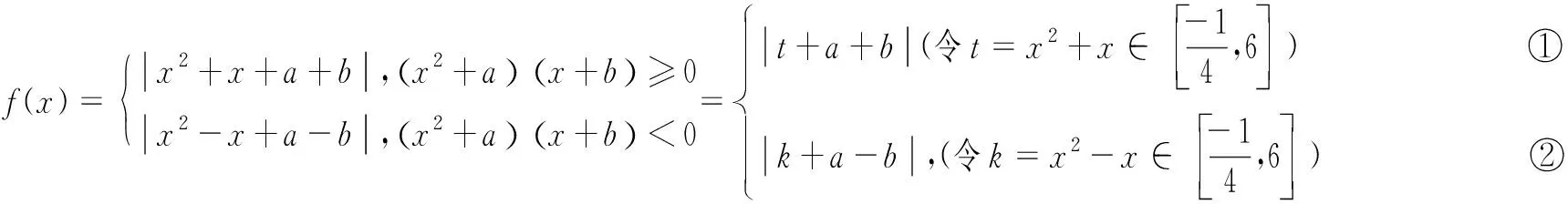
点评以上三种方法应该说是解决绝对值函数问题最基本的手段,三种方法核心之处在于都用了一个重要恒等式|a|+|b|=max{|a+b|,|a-b|},其本质是把两个绝对值问题转化为一个绝对值问题进行研究,自然可以从绝对值函数图象与值域,绝对值三角不等式,以及绝对值的几何意义等方面思考,水到渠成.
3 新的解法探究
如前解法,我们习惯于利用降维的思想,将两个绝对值减为一个绝对值,其实两个绝对值之和结构本身也具有良好的几何意义.下面仍从三个不同的几何视角给出新的认识.
视角四我们知道在线性规划里|x|+|y|=1是一个对角线长度为2的正方形,那么|x|+|y|=k呢?显然可以当成对角线长度为2k并随着k的变化可以缩放的正方形.
解法4f(x)=|x2-(-a)|+|x-(-b)|=|y-(-a)|+|x-(-b)|≤M(记y=x2,x∈[-2,2]),则点(x,y)的轨迹可以视为以(-b,-a)为对称中心,对称轴垂直于坐标轴的正方形内部(含边界).随着M的变化,正方形的大小变化.
故题意即为画一个正方形,要求抛物线y=x2,x∈[-2,2]完全包裹在正方形内.
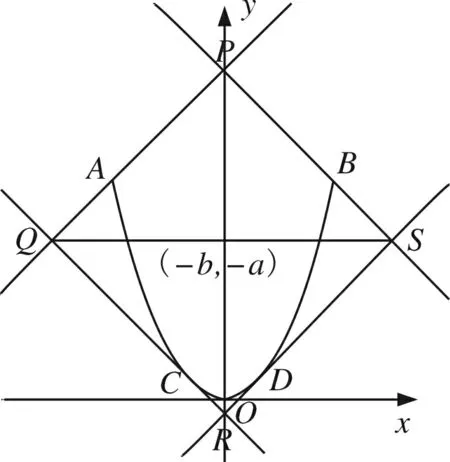
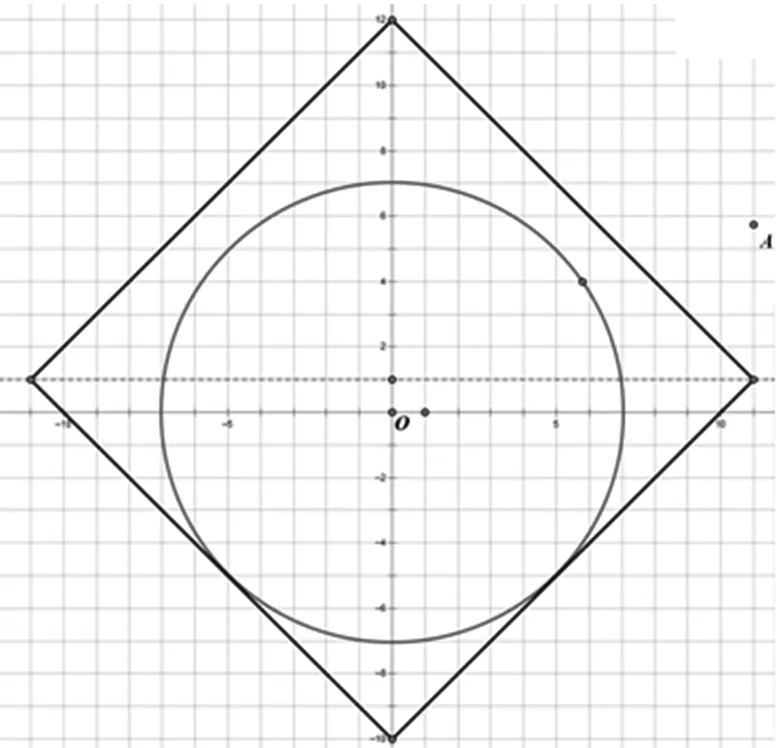
同样的方法我们可以巧妙而快速地解决2017年浙江省金华市十校模拟卷中的填空压轴题,如下:
已知y=|asinθ+bcosθ|+|bsinθ-acosθ-1|的最大值为11,求a2+b2的值.
解令u=asinθ+bcosθ,v=bsinθ-acosθ,
则u2+v2=a2+b2=r2.
|u|+|v-1|=Z,随着Z的变大,正方形逐渐变大,当正方形边界与圆相切时,取得Zmax=11.
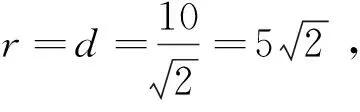
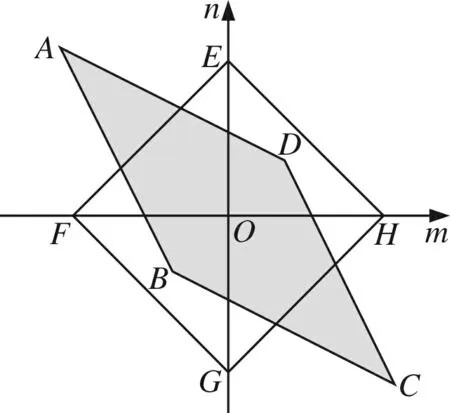
再比如2018绍兴市高一第二学期期末卷中选择题压轴题:
已知a、b是实数,对任意的x∈R,都有|asinx+b|≤1成立,则|a+3b|+|a-3b|的最大值为________.
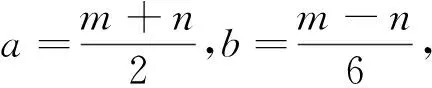
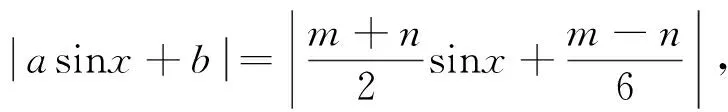
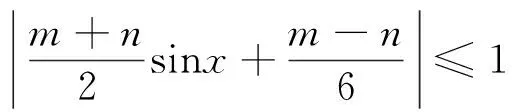
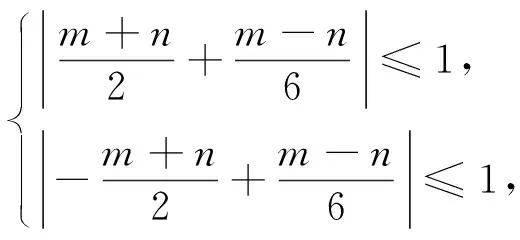
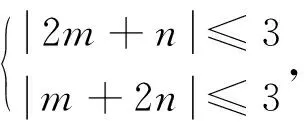
视角五两个绝对值之和除了几何意义可以表示为四边形外,还有什么其他意义呢?其实在现实生活中也有它的背景——曼哈顿距离.
【数学史小链接】 曼哈顿距离
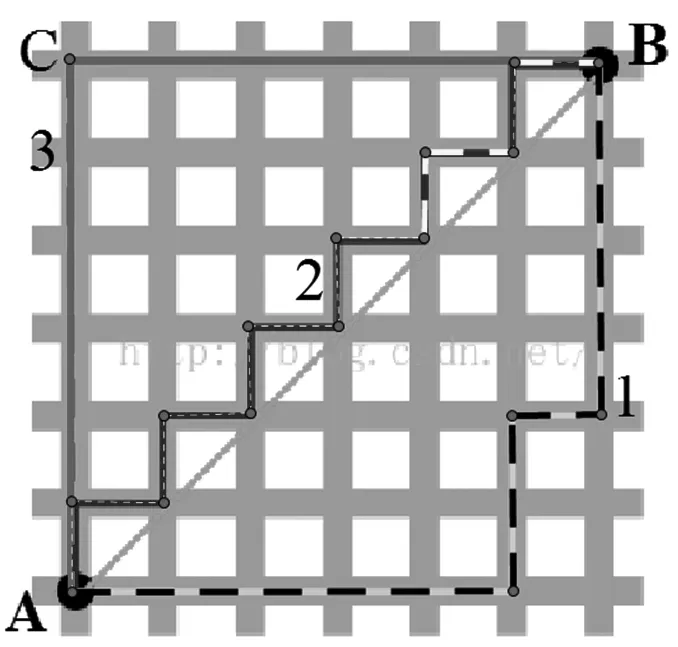
曼哈顿距离(Manhattan Distance)是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ,是一种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和.曼哈顿的街道纵横交错(如图),若要从A地经过C地到达B地,行走的最短距离显然是|AC|+|BC|.在Rt△ACB中,我们用|AC|+|BC|来表示AB间的折线距离,这种表示法就是著名的曼哈顿距离,又称为出租车几何.如图,我们也可以发现三种线型的不同路径(1,2,3)都对应AB的曼哈顿距离.
数学表示如下:
点A(x1,y1)与点B(x2,y2)之间的曼哈顿距离为:d(A,B)=|x1-x2|+|y1-y2|.
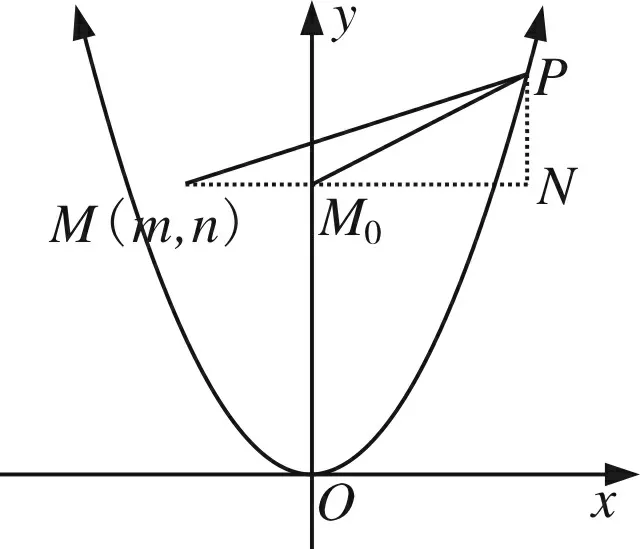
解法5f(x)=|x2-(-a)|+|x-(-b)|=|x2-n|+|x-m|.
这个目标函数式可以理解为点P(x,x2)与点M(m,n)之间的“曼哈顿距离”dMP=|MN|+|PN|.
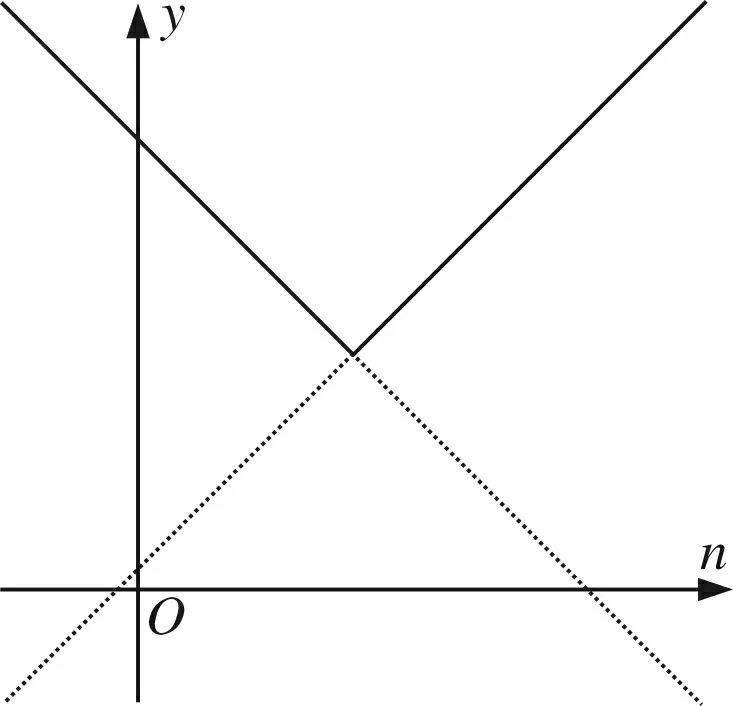
如图,显然由对称性,当M(m,n)在y轴上,即M0(0,n)时,dMP取得最大值的最小值,即dmax=|x2-n|+x.
注意到点M0(0,n)(n≥0)与点P(x,x2)(0≤x≤2)都可以运动,那么不妨先让点M0(0,n)不动,点P(x,x2)运动.
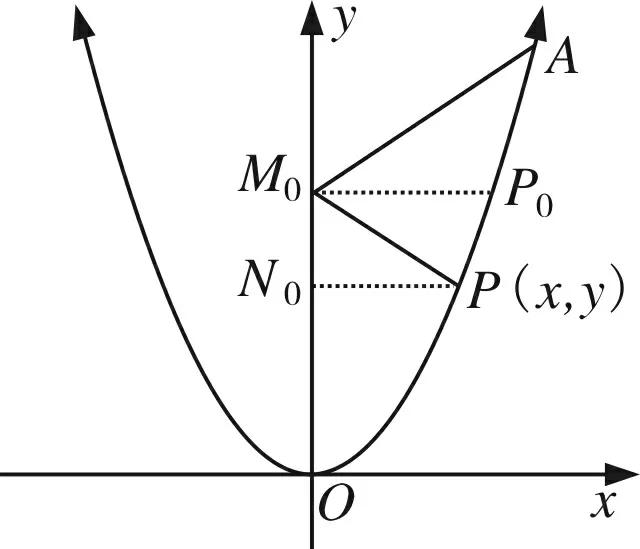
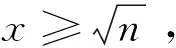
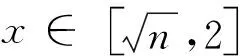

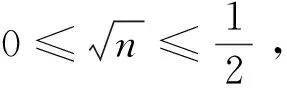
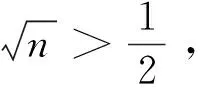
所以结合(1)可得结论
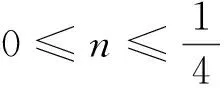
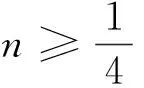
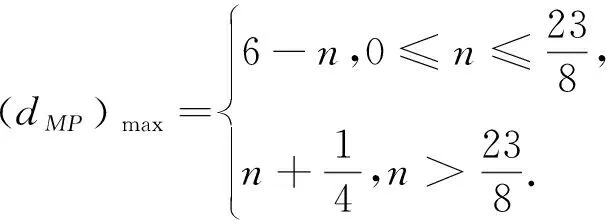
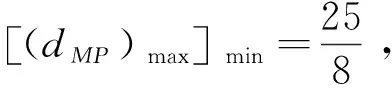
点评本解法将目标式子视为“曼哈顿距离”的视角非常精巧,后面两动问题的处理也顺理成章,但分类讨论的能力要求较高.如果只是填空题,不少学生和老师会直接取临界状态,虽然少了解法中的严格说明过程,但也不失为一种巧解.
其实“曼哈顿距离”在高考中出现很多次,甚至可以有更多的形态,包含了很多变形与创造,形如2014江西高考理科第11题.
对任意x、y∈R,|x-1|+|x|+|y-1|+|y+1|的最小值为( )
A.1 B.2 C.3 D.4
解此题即求平面内动点P(x,y)到两个定点A(0,-1),B(1,1)间垂直于坐标轴的方向的“曼哈顿距离”,显然最小值为3,故选C,当且仅当P的轨迹是矩形区域内即可.

而2014年的浙江高考理科第10题,“曼哈顿距离”若隐若现.
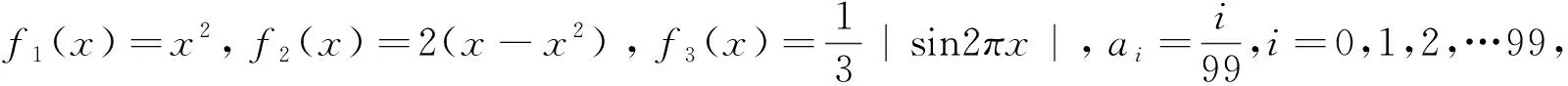
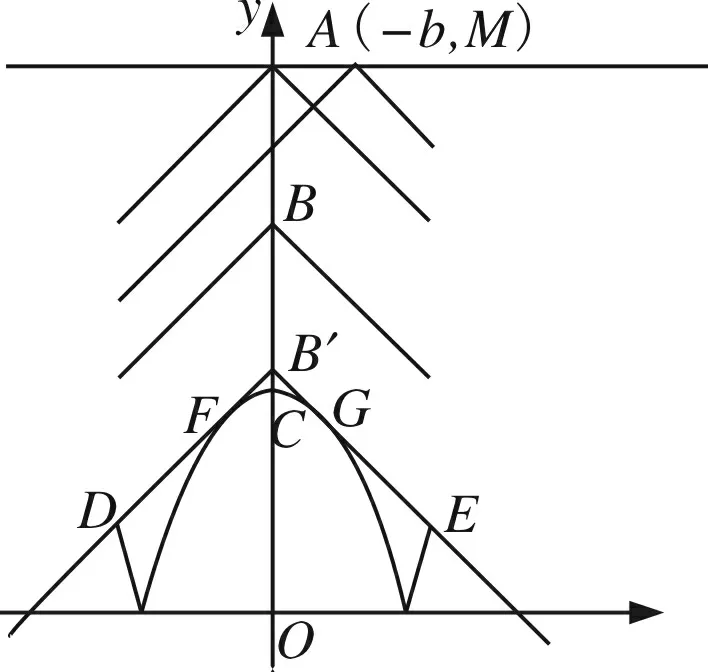
A.I1 C.I1 解不妨取一个区间x∈[0,1],显然|a1-a0|+|a2-a1|…+|a99-a98|=1, 目标Ik进行变形,即Ik=|fk(a1)-fk(a0)|+|fk(a2)-fk(a1)|+…+|fk(a99)-fk(a98)|=|fk(a1)-fk(a0)|+|fk(a2)-fk(a1)|+…+|fk(a99)-fk(a98)|+|a1-a0|+|a2-a1|+…+|a99-a98|-1,问题的实质表示质点从原点出发,沿函数图到达点(1,0),相邻两个点ai与ai-1之间的“曼哈顿距离”之和,由于水平方向所走的路程均为1,故只需比较竖直方向上所走路程之和大小的问题,如图得: 视角六分拆函数,V型函数开路 解法6 |x2+a|+|x+b|≤M在x∈[-2,2]上恒成立, 即|x2+a|≤M-|x+b|在x∈[-2,2]上恒成立, 即y1=|x2+a|的图象恒在y2=M-|x+b|(x∈[-2,2])的下方. 如图随便画一个y1=|x2+a|的大致图象,y2=M-|x+b|是一个开口向下的V字图,其中尖角的点在A(-b,M), 要使M尽可能小,显然在b=0处取得. (由图可以解释,如图当点A(-b,M)在如图点A处,V字图可以先向左平移,再向下平移,尖角到达点B处时,向下的V字图到达临界状态). 故题目简化为|x2+a|≤M-|x|在x∈[-2,2]上恒成立,求M的最小值. 接着让a变化,显然当点C越来越高,点D、E越来越低时,向下的V字图还可以继续下移,直到如图的临界状态. 点评本解法是用动静分离的手段,将不等关系转化为两个函数图象的位置问题.尤其是两动问题,“一定一动,先定后动,逐步调整”的原则更是重要. 新的视角呈现的三种解法,也是对两个绝对值处理的一种新的理解.从此题的探究过程中,我们有这样的认识,双绝对值直接理解就是两个点之间的曼哈顿距离,若是换一个视角那么双绝对值的几何意义可以认同为正方形的对角线长度.我们在解题中若是从不同视角多样化处理,那么我们的问题会变得层次分明,更有意思,我们学习数学的兴趣也会被更好地激发. 浙江高考《考试说明》明确指出高考试题对学生的个性品质提出了要求.何谓个性品质?个性品质是指学生个体的情感,态度和价值观,提高学习数学的兴趣,树立学好数学的信心,形成锲而不舍的钻研精神和科学态度.具有一定的数学视野,逐步认识数学的科学价值、应用价值和文化价值,形成批判性的思维习惯,崇尚数学的理性精神,体会数学的美好意义. 作为教师,首先要自己打开解题的思维,在教学过程中尽可能增加一些视角,方能在课堂上引导学生去尝试用不同的眼光审视数学的问题,感受数学解题过程中的乐趣,思考哪种思维方式更适合自己,从而塑造自己独特的个性品质.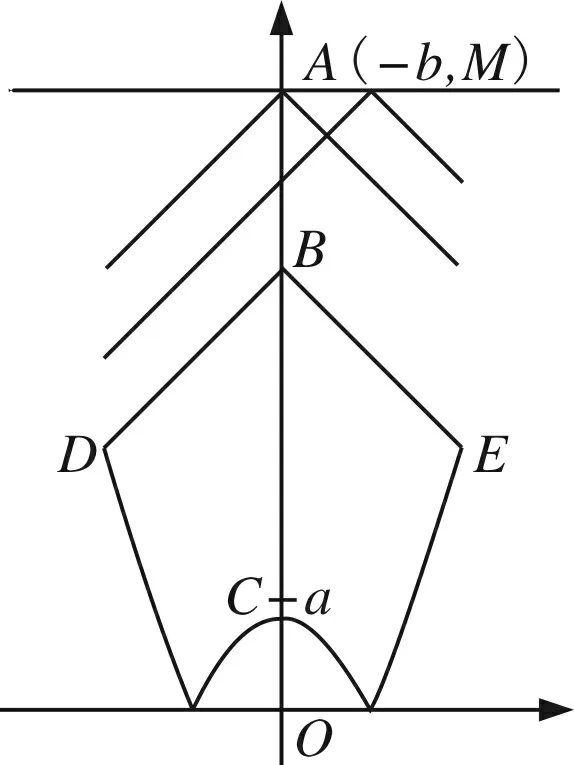
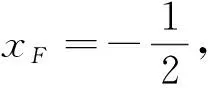
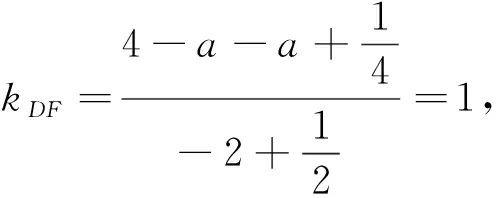
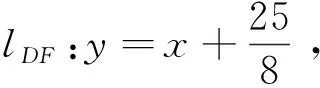
4 解题反思
