一道几何问题的数学本质探析

四川省巴中市巴州区大和初中 (邮编：636031)

在某数学QQ群里，大家对一道几何最小值问题的解法展开了讨论，其中，比较有代表性的解法思路有两种，但其合理性及问题数学本质，引发质疑和探究，现将笔者的探究结果与大家分享.

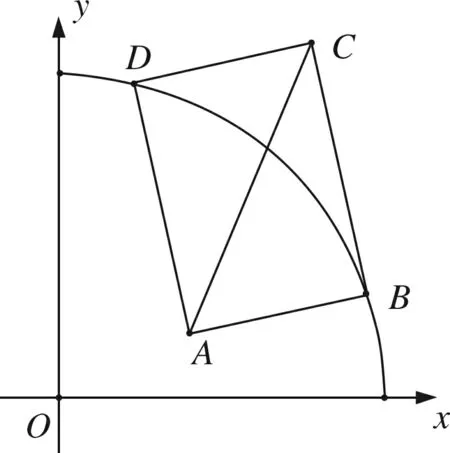
图1

题目如图1，在平面直角坐标系第一象限有一半径为5的四分之一⊙O，且⊙O内有一定点A(2,1)，B、D为圆弧上两点，且∠BAD=90°，以AB、AD为边作矩形ABCD，则AC的最小值为__________.

1 问题提出

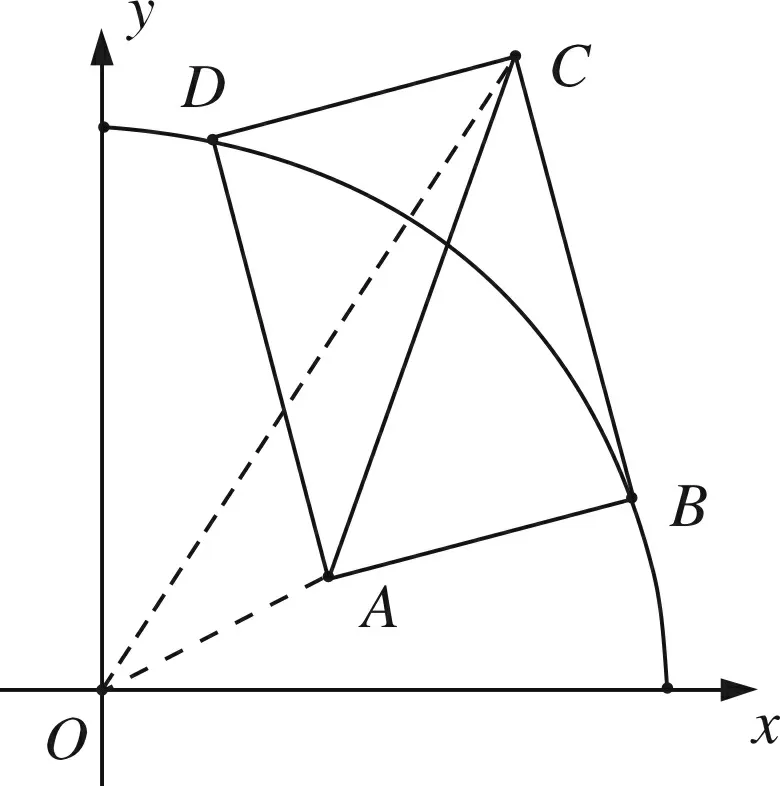
图2

解法1 如图2，根据三角形三边关系定理，得AO+AC>OC，因为AO是定值，要使AC最小，只需OC最小，只有O、A、C一线时OC最小，此时AC也最小.

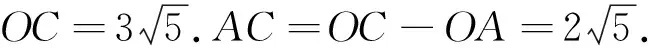
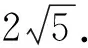
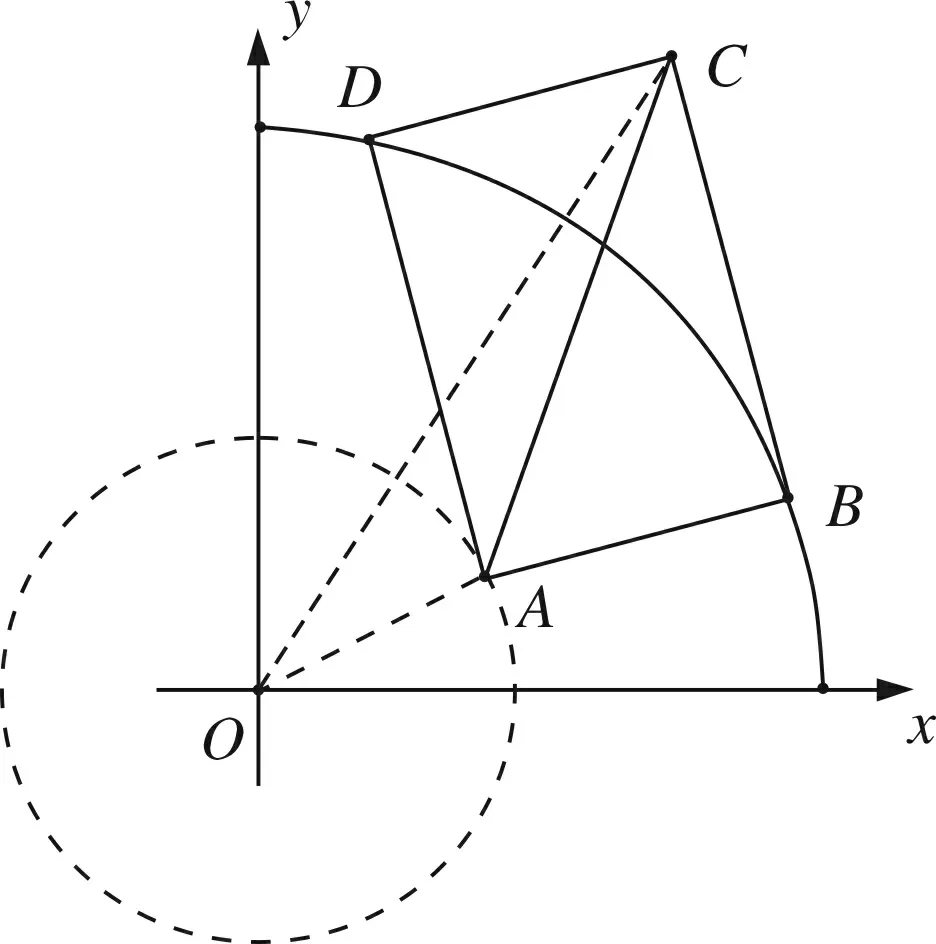
图3

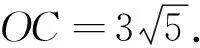
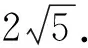
质疑上述解法的相同点都运用了矩形的一个结论：OA2+OC2=OB2+OD2，为什么？不同点是数学模型各异，解法1依据“三角形三边关系定理”，但该模型中的三点不可能共线，而问题中的O、A、C可能共线.解法2依据“圆外一点到圆的最短距离”，但该模型条件中圆外一点应是定点，而点C是动点.

2 问题解决

2.1 矩形的一个性质

矩形所在平面内任一点到相对的两个顶点的距离的平方和相等.

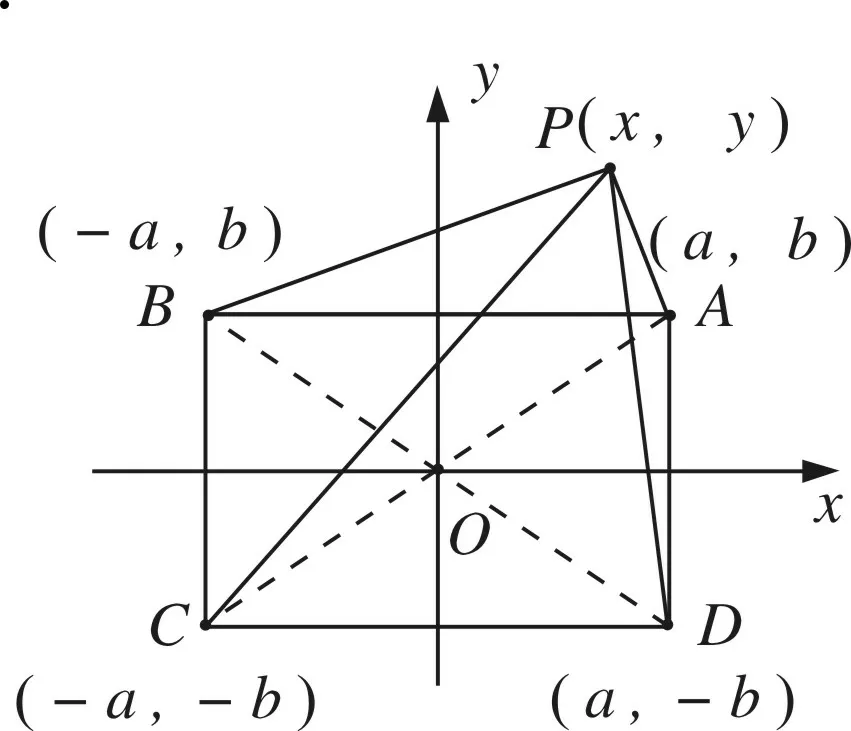
图4

证明如图4，以矩形ABCD对角线交点为原点，平行于矩形两边的直线为坐标轴建立直角坐标系，则每条对角线的两端点关于原点成中心对称.

设矩形ABCD的四个顶点分别为A(a,b)，C(-a,-b)；和B(a,-b)，D(-a,b). 再设矩形所在平面内任意点P(x,y)，则PA2+PC2=(x-a)2+(y-b)2+(x+a)2+(y+b)2，PB2+PD2=(x+a)2+(y-b)2+(x-a)2+(y+b)2，显然，PA2+PC2=PB2+PD2.

即矩形内任意一点到相对的两个顶点的距离的平方和相等.

2.2 解法合理性改进

对于解法1，由于点O为定点，OC为定长，应用“两点之间线段最短”模型”更为恰当.

正确解法根据两点之间线段最短，得AO+AC≥OC，即AC≥OC-OA，当O、A、C一线时AC最小.

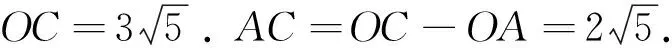
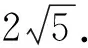
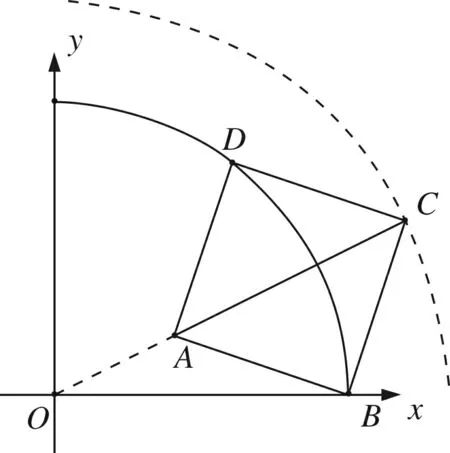
图5

对于解法2，因点O为定点，OC为定长，所以点C在以点O为圆心，OC长为半径的圆上，点A为这个圆内一点，应改用“圆内一点到圆的最短距离”模型.

正确解法如图5，在矩形ABCD中，OA2+OC2=OB2+OD2，所以OC2=OB2+OD2-OA2，OA2=12+22=5.

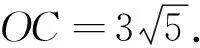
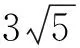
过点A作半径OC，则AC最小.

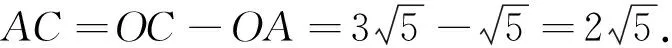
思考1 当O、A、C共线时，AC最小，此时，点B是否一定位于第一象限呢？

当点A在半径OC上时，根据对称性，得AB=BC.直线OA的解析式为y=0.5x，设点C(2y，y).所以(2y)2+y2=OC2=45，解得y=3，于是C(6，3).

设点B(a，b)，则(a-2)2+(b-1)2=(a-6)2+(b-6)2=10.

解得a=3，b=4(舍去)；a=5，b=0.

所以B(5，0)，即点B在x轴上.

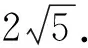
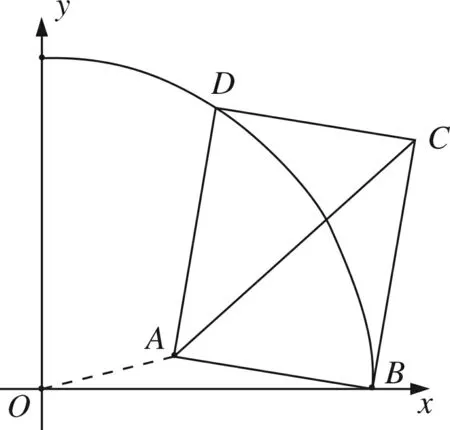
图6

如图6，将条件修改为A(2，1.5)，其余不变.点B是否在第一象限呢？

如图7，利用几何画板软件作图，将矩形ABCD绕点A顺时针旋转，发现：AC逐渐减小，至点B在x轴上时，AC最小，但O、A、C三点并不在一条直线上.如果要符合O、A、C三点在一条直线上，矩形必须突破第一象限，跨越到第四象限才行.这个问题具有一定隐蔽性，容易引发错误.

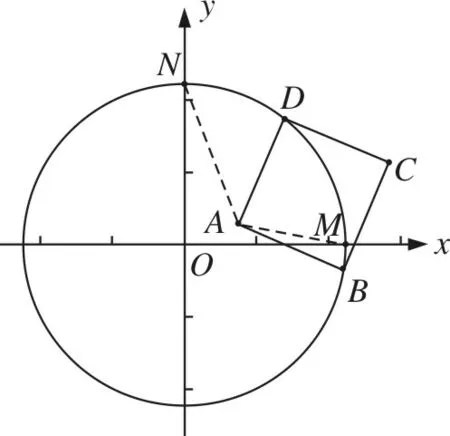
图8

3 图形范围探究

满足O、A、C三点在一条直线AC最小，图形范围如何界定呢？

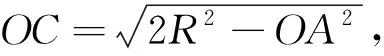
因点A在第一象限，设⊙O与x轴及y轴正半轴分别交于点M、N.

(1)当AN≤AB≤AM时，矩形ABCD在第一、二象限内；

(2)当AN≥AB≥AM时，矩形ABCD在第一、四象限内；

(3)当AN≥AB≤AM时，矩形ABCD在第一象限内.

拓展如果点A第二、三、四象限呢？有类似结果.

特别地，当点A在坐标轴上，取最值时矩形会在哪些象限呢？

当点A在x正半轴时，矩形ABCD在第一、四象限；

当点A在x负半轴时，矩形ABCD在第二、三象限；

当点A在y正半轴时，矩形ABCD在第一、二象限；

当点A在y负半轴时，矩形ABCD在第三、四象限.

这样，不解最值，可先判断AC最小时，矩形经过的象限.

譬如文前问题：由于

若

因AN≥AB≤AM，所以矩形ABCD在第一象限内，矩形不会跨入第二象限，而且AB=AM，则点B与点M重合.满足O、A、C三点在一条直线上时，AC最小.

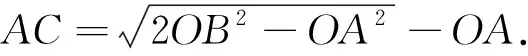
思考2 如果题设条件只限定在第一象限，如何求最小值AC呢？

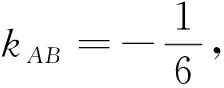
(负值已舍).

所以

根据两点间距离公式，得

4 建议

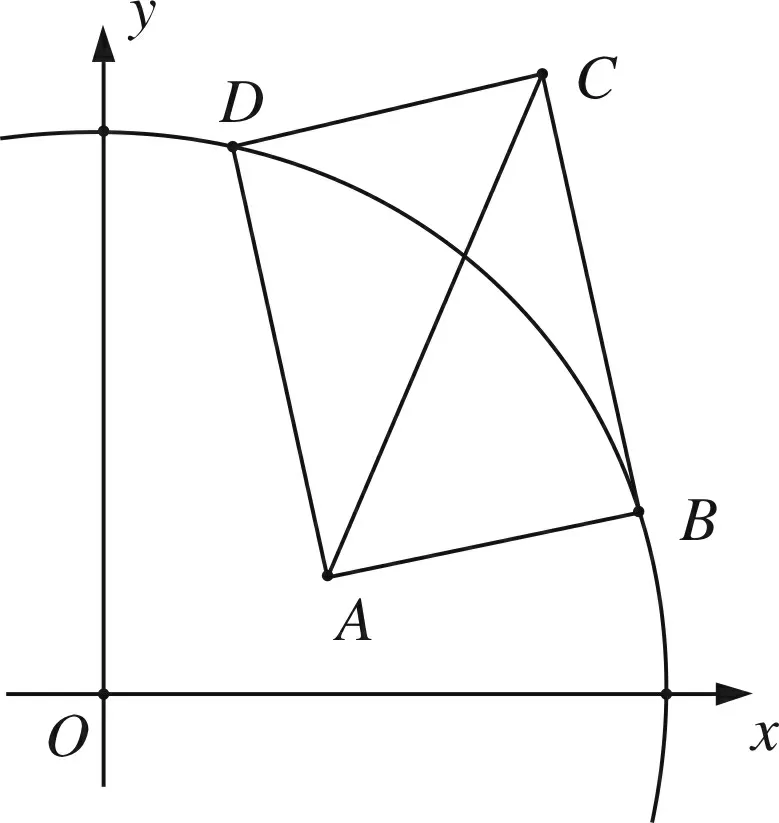
图9

为体现严谨性，同时降低解题难度，将题目中的象限扩至相关象限或取消象限要求，确保始终在O、A、C三点在一条直线时，AC最小.

譬如：如图9，在平面直角坐标系内有一半径为5的半⊙O，且⊙O内有一定点A(2,1)，B、D为圆弧上两点，且∠BAD=90°，以AB、AD为边作矩形ABCD，则AC的最小值为__________.

这样，解法1和解法2的思路，也都是严谨正确的了.

思考3 将题目中的矩形改为内角不变的平行四边形，其余条件不变，AC的最小值还存在吗？显然存在，只是上述解法不再适合.

可以大胆猜想，一定小心求证.思维缜密性是数学思维的重要指标之一，它是指在分析和解决问题的过程中，周到而细致地考虑问题的一种思维品质，无论是命题工作，还是教学工作都应在严谨科学精神指导下完成.