基于自适应H-极大值的粘连颗粒分割算法
2018-12-22何磊王正勇滕奇志田刚
何磊,王正勇,滕奇志,田刚
(1.四川大学电子信息学院,成都 610065;2.新疆油田公司行政事务中心,克拉玛依 834000)
0 引言
随着CT岩心扫描成像技术日益成熟,利用CT岩心序列图重建出岩心三维结构成为一种重要的数字岩心分析手段。由于岩心中岩石颗粒相互挤压和粘连,在对岩心三维图像进行颗粒的粒度分析时,存在的粘连颗粒会影响颗粒的参数计算准确性。目前针对粘连颗粒分割的问题,研究者们根据岩心三维体颗粒(如图1所示)具有类球性差、轮廓信息不规则以及数据量大等特征,提出了不同的思路:

图1 CT岩心序列图
(1)基于腐蚀膨胀的粘连分割方法[1]。此方法对粘连颗粒进行连续腐蚀操作,直至粘连颗粒分开,再进行膨胀操作恢复颗粒。特点是原理简单,运算速度快,对粘连程度较小的颗粒能实现快速准确分割,但是针对粘连程度较大的颗粒,存在腐蚀次数不易控制和目标形变严重等问题。
(2)基于骨架的分割方法[2]。此方法通过统计垂直于颗粒骨架的截面的变化规律来进行分割。但是骨架提取算法和截面变化规律统计的计算量大,并且容易受到噪声的影响而出现一些冗余的骨架段,不适合形状复杂的岩石颗粒分割。
(3)基于分水岭的分割方法[3]。此方法利用二值图的距离变换图中的局部极大值作为种子点,实现分水岭分割。但是因为岩石颗粒的形状复杂以及噪声点,距离变换矩阵中会出现冗余的局部极大值点,会导致严重的过分割现象。本文借鉴分水岭算法的思想,提出了一种三维粘连颗粒的分割算法:利用自适应的H-极大值变换抑制冗余的局部极大值[4],然后以岩石颗粒的最优形状因子作为目标函数,利用基于三维颗粒粘连程度的合并算法进行区域合并,从而得到最终的分割结果[5]。
1 岩石颗粒形状度量指标
颗粒的球度公式定义由Wadell[6]提出,其文中通过计算颗粒等效球的表面积和颗粒表面积(颗粒等效球为与颗粒体积相等的球),得到两者的比值即为球度,球度公式如下:

其中Se为颗粒等效球的表面积,Sp为颗粒的表面积。公式(1)是作为经典公式被广泛使用,文献[7-9]均采用此球度公式作为颗粒的形状度量,其中文献[9]将公式(1)变换成二维的圆度公式,分别计算三维颗粒在x、y和z方向投影对应的三个圆度值,取三个圆度值的加权平均值作为颗粒的形状度量。
另外,文献[10]提出形状因子计算公式:

其中,V表示颗粒体积,Sp表示颗粒表面积。Φ的取值范围是(0,1],颗粒形状越接近于球,Φ的取值越接近于1,若颗粒形状呈现面状,则Φ的取值趋向于0。公式(1)形状因子表达式与公式(2)球度表达式具有相近的数学内涵,把颗粒体积V代入式(1)中得到式(3):

在程序的计算过程中,式(1)需要计算颗粒等效球的表面积Se,Se的计算首先需要计算颗粒体积V,然后由球的体积与表面积之间的关系式推导出Se,而式(2)没有推导Se的步骤,得到颗粒体积V和颗粒表面积Sp即可计算形状因子。本文对于岩石颗粒的形状度量采用公式(3)。
2 基于自适应H-极大值的粘连颗粒分割算法
岩石颗粒具有边缘复杂和形状不规则的特征,传统分水岭变换能将粘连的颗粒分割开,但是容易产生如图2所示的过分割现象。因为颗粒的距离变换图中普遍存在不止一个局部最大值的情况,直接选取每个局部最大值点作分水岭变换的种子点会产生严重的过分割现象。本文通过使用H-极大值变换来抑制冗余的局部极大值点,同时加入第1节定义的岩石颗粒形状度量指标实现了自适应的H-极大值变换,为了防止h值的增大导致正确的局部极大值点被过滤掉,H-极大值变换后的子分割区域集合还加入了区域合并算法。另外,由于经过三维重建的岩石颗粒的表面以及邻域空间会产生许多细纹以及噪声点,在进行H-极大值变换之前利用开重建运算去除因三维重建过程中产生的噪声点[11]。

图2 分水岭变换的过分割现象
2.1 自适应H-极大值变换
分水岭变换[12]的过程可以理解为降雨的过程,最后得到集水盆的集合,不同的集水盆对应不同的目标区域。因为一个集水盆对应于距离变换矩阵的一个局部极大值区域。所以过分割意味着有冗余的局部极大值点,要解决过分割就是要去除冗余的局部极大值点。
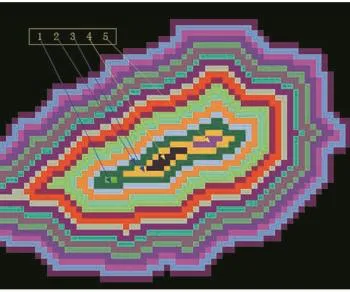
图3 颗粒的距离变换图
如图3所示,黑色像素点为背景,不同颜色的像素点代表不同的距离值,距离值由目标边缘向目标中心逐渐增大,局部极大值存在于目标中心区域。上图中我们期望的颗粒数是1,即只出现一个局部极大值,但图中存在3个局部极大值区域1、4、5(对应的距离值分别为17、19和20)。如果直接用分水岭变换,会得到三个目标,这显然是错的。因为距离变换受目标的局部噪声的影响出现了多个局部极大值,如果有办法过滤掉多余的局部极大值点,使得过滤后的局部极大值点的数目与我们期望的颗粒数目一致,就能得到正确的结果,达到抑制过分割的目的。
H-极大值变换[13]的作用是过滤掉距离值小于阈值h的冗余局部极大值点。h=0为起始点,通过以Δh=0.5逐步增大h值,逐步减少子分割区域的数目,找到能使当前子分割集合的加权平均形状因子最大的h值,从而实现自适应的H-极大值变换。加权平均形状因子公式和变换公式如下:

上述公式中Vtotal表示子分割区域的总体积,vi表示子分割颗粒的体积表示对应h值变换下的加权平均形状因子,maxpts表示子分割区域最大的局部极大值,hmax则表示子分割区域最终的H-极大值变换使用的h值。其中表示对标记图像I的测地膨胀,标记图像I是原图像的距离变换矩阵中局部极大值点的集合。
图4展示了不同h值对应不同岩石颗粒子分割集合的加权平均形状因子。图4(b)是原始图像(a)的分水岭算法分割结果,可见一颗完整的颗粒被过分割成三颗颗粒。逐步增大h值,直到h值增加到5也不能抑制过分割的情况,说明冗余的局部极大值大于5。当h值为5.5时,如图4(c)所示,一个冗余局部极大值被过滤掉。当h值为8时,图4(a)中两个冗余的局部极大值点均被过滤掉,得到子分割结果(d),此时加权平均形状因子最大,所以h=8对应的H-极大值变换得到的子分割集合作为候选结果。以此类推,对每个连通区域都可自适应地选取最优h值。
2.2 合并规则
合并规则是作为h值的继续迭代的约束条件,防止h值的增大把正确的局部极大值点也过滤掉,从而导致欠分割现象。由于岩心三维颗粒的类球性较差,粘连复杂,为此本文提出了基于粘连程度合并规则,这样合并规则的适应性会更强。粘连程度定义如下:

如图5所示,展示了两个粘连颗粒分水岭变换的距离变换图,b和c表示两个粘连颗粒的局部最大值,即为分水岭变换选取的种子点,a表示粘连处的局部最大值。当两个颗粒的粘连程度大于设定的阈值,就合并这两个颗粒。如果粘连阈值过大,会导致部分过分割的颗粒无法合并。如果阈值过小,会让本来不该合并的两个颗粒合并。本文通过多次实验对比分割效果,选取分割效果最好的粘连阈值,本文实验结果对应的粘连阈值为0.8。为了便于观察且说明问题,采用程序随机生成的球型数据为实验对象,如图6所示,展示了不同粘连阈值对应的不同的合并效果。

图4 岩石颗粒的h值以及形状因子

图5 粘连程度的定义
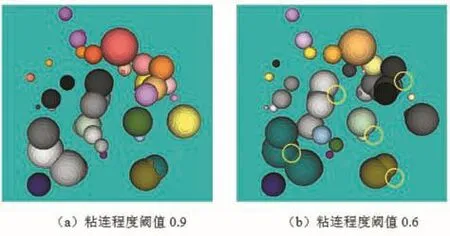
图6
2.3 算法步骤
定义图像经过开重建滤波处理后的N个连通分量集合I={Ij|j∈{1,2,…,N}}。对每一个Ij先后进行距离变换和分水岭分割,得到初始分割结果。定义Ij={Sn(Ij)|n∈{1,2,…,m}}为每个连通分量的初始分割结果,分割后的子区域为m个,需要对m>1的连通分量进一步处理,m=1的连通分量为最终分割结果。进一步处理的算法如下:
(1)初始化连通分量的序号j=1;
(2)取连通分量Ij,及其初始分割结果Sn(Ij),n∈{1,2,…,m},子分割数目是m,初始化阈值h=0,最优平均形状因子opt_shape=0;
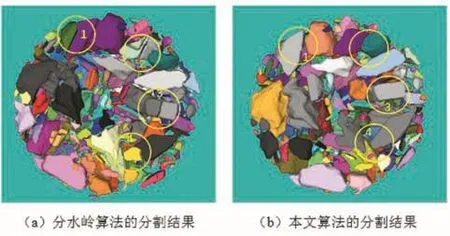
(3)当mj(h)>1且mj()h (4)若opt_shape<ϕ,则则跳转至 f); (5)令h=h+Δh,进行阈值为h的H-极大值变换,跳转至 c); (7)j=j+1,若j 本文算法应用在由岩心CT序列图重建得到的三维模型。如图7所示,由两组CT序列图提取出岩石颗粒分别得到图7(a)和(b)所示的岩石颗粒三维模型,然后对三维模型中的岩石颗粒进行分割,图7(a)和(b)对应的分割结果分别为图8和图9。图8(a)为传统分水岭算法分割后的三维模型,图8(b)为本文算法分割后的结果,两图均为伪彩色图像,不同颜色的三维体目标代表分割后的岩石颗粒。图8中标识的1、2、3和4显示了两种算法效果的差别,由图可见本文算法有效抑制了传统分水岭的过分割现象。对于形状复杂且不规则的颗粒图像,在最优加权平均形状因子和合并规则约束下,H-极大值变换能保证每一个分割后的颗粒都接近于真实情况。 图7 图8 图9 针对三维模型中存在岩石颗粒粘连的问题,本文提出了一种基于自适应H-极大值的粘连颗粒分割算法,对实际工程中遇到的三维粘连颗粒进行了分割。实验结果表明,本文提出的算法具有分割准确的优点,能够解决实际工程中三维粘连颗粒的分割问题。3 实验结果对比与分析


4 结语
