网络零售额影响因素模型研究

胡静波，朱丽丽,2

1.合肥通用职业技术学院基础部，合肥，230031;2.中国科学技术大学管理学院，合肥，230026

1 相关研究与问题提出

随着社会信息化和网络化步伐的加快，网络销售在带给消费者极大便利和实惠的同时，也带来了相当可观的经济效益和社会效益。根据商务部、国家统计局、中国电子商务研究中心等机构公布的数据，我国网络零售额呈逐年快速上升趋势，从2005年的150亿元增长到2017年的71 751亿元，年均增长率高达67.23%。因此，在“互联网+”的时代背景下，网络销售业既面临着新的挑战，也面临着无限的市场机遇。国内学者对网络零售发展现状[1]、网络零售的影响因素及发展策略[2]进行理论研究。

R语言是一种功能强大的、为统计计算和图形显示服务的语言环境，具有比其他统计学或数学专用的编程语言更为强大的面向对象的功能，使用者只需输入数据和参数即可进行统计分析[3]。近年来，统计学应用的新兴研究领域之一就是运用R语言等机器语言针对现实问题构建数学模型。陈将浩利用R语言实现了对房价影响因素的分析[4]；栾汝朋等人运用R语言构建了一种适用于Web日志挖掘的关联规则算法模型[5]；王怀亮讨论了数据挖掘中的线性回归技术及R语言实现[6]。

本文借助多元线性回归分析法，运用R语言对网络零售额影响因素进行探讨，从理论研究和实证研究两方面科学选择最合适的自变量，尝试建立网络零售额影响因素的数学模型。

2 网络零售额影响因素

在我国社会主义市场经济体制下，网络零售业的发展受到国内生产总值、社会消费品零售总额、经济指数、人口数量等宏观经济因素和社会因素的影响。为了便于分析，笔者将网络零售额的影响因素划分为经济因素、经济指数、人口因素三个方面。

本文选取的数据从2005年1月开始，到2018年6月结束(多项可供公开查询的相关数据起始时间为2005年)。数据来源如下：全国网络零售额、快递业务量主要来自商务部、国家统计局、中国电子商务研究中心、国家邮政局等机构公布的数据；国内生产总值、社会消费品零售总额、全国城镇居民人均可支配收入、居民消费价格指数、商品零售价格指数、工业品出厂价格指数来自国家统计局发布的《中国统计年鉴》《中国国民经济和社会发展统计公报》；物流费用率来自国家发展改革委经济运行调节局等部门公布的《全国重点企业物流统计调查报告》；网络购物用户规模、手机网民比例、农村网民比例、女性网民比例来自中国互联网络信息中心发布的《中国互联网络发展状况统计报告》《中国网络购物市场研究报告》；消费者信心指数来自于中国金融在线旗下的证券之星财经网站。因篇幅有限，本文未贴出R语言代码、部分图表及数据。

2.1 经济因素

由于影响网络零售额的经济因素众多，本文选取与之关系密切且具有代表性的国内生产总值、社会消费品零售总额、城镇居民人均可支配收入、快递业务量、物流费用率等5项指标进行影响因素分析，并采用了2005—2017年共13组相关因素的年度数据，如表1所示。

表1 2005—2017年全国网络零售额与经济因素数据

首先对全国网络零售额和5个经济因素的均值、最值、中位数、标准差进行描述性统计分析，输出结果如表2所示。

表2 2005—2017年全国网络零售额与5个经济因素的描述性统计

由表2可知，网络零售额与4个经济因素(国内生产总值除外)的中位数小于均值。这说明这几个变量的增长随着时间逐步加快。再利用cor.test函数中的Pearson检验分析变量之间的相关系数，输出结果如表3所示。

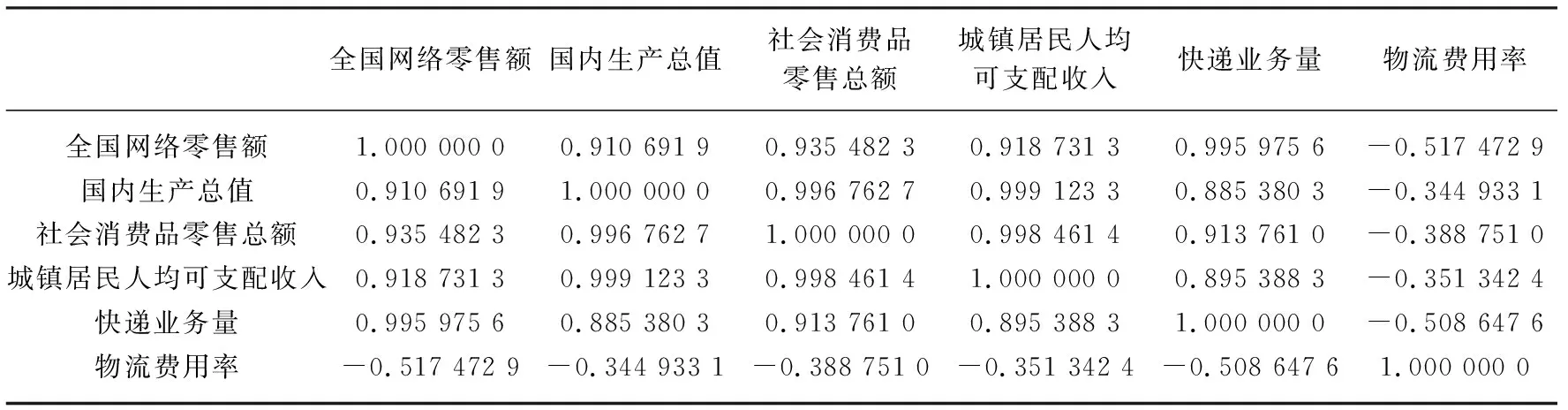
表3 2005—2017年全国网络零售额与5个经济因素的相关系数

由表3可知,国内生产总值、社会消费品零售总额、城镇居民人均可支配收入、快递业务量与网络零售额不仅正相关，而且相关性极强；物流费用率则与网络零售额负相关，且仅为中等强度相关。国内生产总值、社会消费品零售总额、城镇居民人均可支配收入等数据的上升，反映国内经济大环境向好的方向发展，居民可用于消费的收入增多了，全国网络零售额自然会随之上升。快递业务量与网络零售额的共同提升也验证了这二者间水涨船高的特点。物流费用的下降，在一定程度上减少了网络零售商的成本，网络商品价格的降低，进一步刺激了网络消费的提升。因此，将经济因素中的国内生产总值、社会消费品零售总额、城镇居民人均可支配收入、快递业务量纳入全国网络零售额影响因素的数学模型中。

2.2 经济指数

首先绘制居民消费价格指数、商品零售价格指数、消费者信心指数、工业品出厂价格指数等4项经济指数自2005年1月至2017年12月的月度数据变化曲线。发现4项经济指数随着时间的推移，有着大致一致的走势，而与全国网络零售额逐渐上升的曲线图对比则差别很大，进一步探讨4项经济指数与全国网络零售额的相关性。

笔者采用2005—2017年的4项经济指数的年度数据进行分析，见表4。

表4 2005—2017年全国网络零售额与经济指数数据

用Pearson检验分析网络零售额与4项经济指数定基数据的相关系数，结果如表5所示。

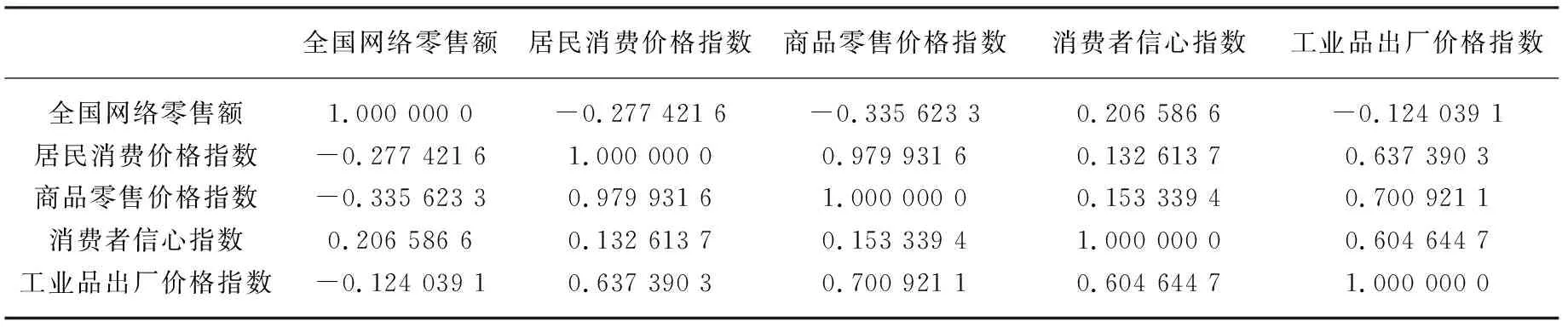
表5 2005—2017年全国网络零售额与经济指数的相关系数

由表5可知，4项经济指数取绝对值后均与全国网络零售额呈现弱相关或极弱相关。由于近年来工业品出厂价格指数的一路走低导致终端消费品价格的下降，在某种程度上刺激了商品网络销售量的增加，提升了网络零售额。因此，经济指数中没有任何一项列入全国网络零售额的影响因素。

2.3 人口因素

在考量人口因素时选择了2005—2017年网民规模、网络购物用户规模、手机网民比例、农村网民比例、女性网民比例共5类13组年终数据，如表6所示。

表6 2005—2017年网络零售额与人口因素数据

通过绘制人口因素变化曲线图发现，网民规模、网络购物用户规模、手机网民比例等3项人口因素的变化曲线与全国网络零售额的变化曲线有着大致相同的上升趋势，而农村网民比例的曲线在2008—2017年间震荡幅度较小且无上升趋势，女性网民比例的曲线在2007—2017年间震荡幅度较大,这两项都与网络零售额的曲线有明显不同。

用Pearson检验分析网络零售额与5项人口因素年度数据的相关系数，输出结果如表7所示。

表7 2005—2017年全国网络零售额与人口因素的相关系数

由表7可知，5项人口因素均与网络零售额呈现正相关。其中，网民规模、网络购物用户规模、手机网民比例、女性网民比例的相关系数>0.5，即与网络零售额强相关。农村网民比例与网络零售额相关性中等。同时，网民规模、网络购物用户规模的增大，手机网民和女性网民的增多，在很大程度上促进了网络零售额的提高。农村网民比例及数量虽有了一定程度的提升，但尚没有转化成网络零售的购买力。因此，将网民规模、网络购物用户规模、手机网民比例、女性网民比例纳入全国网络零售额的影响因素数学模型。

3 模型优化

3.1 模型Ⅰ

通过前面的分析可知，全国网络零售额与国内生产总值、社会消费品零售总额、城镇居民人均可支配收入、快递业务量、网民规模、网络购物用户规模、手机网民比例、女性网民比例这8个变量具有较强的相关性。

为进行函数构建，假设yi:全国网络零售额；x1:国内生产总值；x2:社会消费品零售总额；x3:城镇居民人均可支配收入；x4:快递业务量；x5:网民规模；x6:网络购物用户规模；x7:手机网民比例；x8:女性网民比例。

笔者将全国网络零售额与8个可能的影响因素进行函数构建：

yi=β0+β1·x1+β2·x2+β3·x3+β4·x4+β5·x5+β6·x6+β7·x7+β8·x8+εi

其中，β0是模型的截距项，β1,β2,…,β8是各个影响因素的回归系数，εi是随机误差项[7]。

在不考虑变量系数的前提下，先建立第一个回归模型Ⅰ：y～x1+x2+x3+x4+x5+x6+x7+x8。

运用从大量数据中压缩提取信息的最常用R语言工具——summary命令分析模型Ⅰ。结果显示，模型Ⅰ调整后的R2高达0.994 6，说明其拟合质量非常好，F统计量的p值只有3.229e-5，说明模型是显著的。但是，模型Ⅰ中除了x4以外的自变量都不显著。由于宏观经济数据经常出现严重的共线性问题，推测模型Ⅰ的多个变量之间可能存在多重共线性。

用kappa检验多重共线性，输出结果为12 723.77。显然模型Ⅰ没有通过多重共线性检验。

3.2 模型Ⅱ

在多元线性回归分析中，常用逐步回归分析的方法，以AIC统计量作为衡量的准则,即选择最小的AIC统计量,用删除变量或者增加变量的方法来优化模型。本文基于AIC统计量，通过step函数逐步回归的方式对模型Ⅰ进行优化，筛选出4个合适的自变量。

以这4个为自变量搭建模型Ⅱ：y～x1+x2+x4+x6。通过summary命令分析模型Ⅱ，结果显示，调整后的R2为0.996 7,拟合质量好。F统计量的p值为1.144e-10。模型Ⅱ是显著的。此外，模型Ⅱ各项的p值都较模型Ⅰ有明显降低。再用kappa命令检验模型Ⅱ的多重共线性，输出结果为8 517.821。显然，模型Ⅱ仍具有严重的多重共线性。

为了进一步降低多重共线性，考虑使用drop1函数计算AIC值，结果如表8所示。

表8 模型Ⅱdrop1命令分析结果

由表8可知，如果去掉变量x1，AIC值的增加量是最少的。此外，拟合越好的方程，其残差平方和应尽量小。如果去掉x1，残差的平方和的增加量也是最少的。因此综合考虑，应该去掉变量x1。

3.3 模型Ⅲ

基于社会消费品零售总额、快递业务量、网络购物用户规模这3个自变量搭建模型Ⅲ：y～x2+x4+x6。

用kappa检验其多重共线性，输出结果为6 850.557。模型Ⅲ的多重共线性数值虽然得到降低，但是仍然高于1 000。为了进一步降低数值，尝试对3个自变量进行对数变换或指数变换。经过测试，发现对x6进行指数变换时，多重共线性数值较低且各个自变量的系数具有显著性。

3.4 模型Ⅳ

模型Ⅳ：y～x2+x4+ex6。用kappa检验其多重共线性，输出结果为593.697 8，这个数值<1 000,且相较于前几个模型的多重共线性数值已大大降低。用summary命令分析模型Ⅳ的回归统计量，结果显示调整后的R2为0.996 5,拟合质量好。F统计量的p值为6.29e-12。由于模型Ⅳ的截距项和各自变量的系数都具有显著性，因此模型Ⅳ是显著的。由于多重共线性普遍存在于经济数据研究中，并且多重共线性对于拟合程度好的模型在进行预测时往往并不影响预测结果。考虑到本模型主要用来预测网络零售额，模型Ⅳ的拟合程度很好，多重共线性降为中等，因此认为模型Ⅳ通过多重共线性检验。

4 模型Ⅳ残差分析

在对模型Ⅳ进行显著性检验和多重共线性检验后，还需要通过残差分析，确保模型Ⅳ的残差通过正态分布检验、同方差性检验以及独立性检验。

4.1 正态分布检验

从模型Ⅳ的回归统计量结果来看，残差的最大值为1 710.40，最小值为-1 717.19，中值为-41.13，残差具有正态分布的特征。下面通过W检验和Anderson-Darling检验加以验证。

首先利用W检验验证模型Ⅳ是否符合正态分布，使用shapiro命令对模型Ⅳ进行检验，从输出结果来看，模型Ⅳ的p值0.413 4>0.05，所以通过正态性假设。

再检测是否能通过Anderson-Darling正态性检验，使用ad命令对模型Ⅳ进行检验，从输出结果来看，模型Ⅳ的p值0.465 1>0.05，顺利通过正态性检验。

4.2 同方差性检验

同方差性即总体回归函数中的随机误差项具有相同的方差。若残差同方差性比较好，则其残差不会随着因变量的变化而变化。这也是为了保证回归参数估计量具有良好的统计性质。加载car程序包，使用ncvTest函数对模型Ⅳ进行同方差性检验。从输出结果来看，由于p值0.821 930 3>0.05，拟合值具有同方差性，因此通过了同方差性检验。

4.3 独立性检验

独立性检验是为了检测残差序列是否自相关。通过car程序包中的durbinWatsonTest函数对模型Ⅳ进行durbin-watson检验。从输出结果来看，由于p值0.052>0.05 ,说明无自相关性，即通过独立性检验。

5 模型建立与预测

模型Ⅳ通过了显著性检验、多重共线性检验、正态分布检验、同方差性检验和独立性检验。根据回归分析的结果，可以确定最终的回归方程：

y=-5 366.30+521.51x2+108.30x4+69.82ex6

国家统计局和国家邮政局的数据显示，我国2017年社会消费品零售总额和快递业务量分别达到36.626 2万亿元和400.56亿件。根据第42次中国互联网络发展状况统计报告，截至2018年6月，我国网络购物用户达5.689 2亿人，半年增长率6.7%[8]。假定社会消费品零售总额、快递业务量、网络购物用户规模这3个指标在2018年的增速与上一年保持一致，则到2018年年底，社会消费品零售总额预计为40.365 7万亿元，快递业务量预计为512.877 0亿件，网络购物用户规模预计达6.070 4亿人。

针对模型Ⅳ运用Predict命令预测2018年全国网络零售额数据。预测结果：最低值为87 591.46亿元，最高值为 115 319.3亿元，合适值为101 455.4亿元。

根据国家统计局公布的2017年国民经济数据，全国网络零售额达71 751亿元。假定近3年年均增长37.01%的速率保持不变，则2018年我国网络零售额预计达98 306亿元。将模型Ⅳ预计的101 455.4亿元与根据年均增长速率预测的98 306亿元相比较，误差在3.20%。

6 结 语

本文采用理论研究和实证研究相结合的方法，对14个可能影响全国网络零售额的因素进行定性分析与定量分析。借助R语言的数据分析，最终选择了社会消费品零售总额、快递业务量、网络购物用户规模这3个因素作为自变量构建数学模型。然后在比较算法结果优劣的基础上进行模型的优化，建立了全国网络购物零售额影响因素模型，最后据此模型预测2018年全国网络零售额达101 455.4亿元。从数学模型上看，社会消费品零售总额、快递业务量、网络购物用户规模这3个自变量与全国网络零售额息息相关。本文通过验证网络零售额影响因素模型且顺利通过多项检验，证明了其科学性、合理性。