三维纺织复合材料增强体结构的矩阵模型研究
2018-12-21杜增锋刘新华
杜增锋,王 旭,2,刘新华,2
三维纺织复合材料增强体结构的矩阵模型研究
杜增锋1,王 旭*1,2,刘新华1,2
(1. 安徽工程大学 纺织服装学院,安徽 芜湖 241000;2. 安徽工程大学 纺织科技公共服务平台,安徽 芜湖 241000)
为了提高三维纺织复合材料增强体结构的设计效率,以贯穿正交机织物为例,在分析交织规律的基础上,提出了反映交织规律的矩阵模型,并给出了矩阵生成的算法。矩阵模型的列向量、行向量分别代表经、纬纱,其中以元素“1”、“0”分别表示接结经纱交织规律的经、纬组织点,以元素“3”、“2”分别表示地经纱交织规律的经、纬组织点,并建立了贯穿正交组织矩阵列向量之间元素的对应关系及矩阵生成算法。研究表明,提出的矩阵模型及其生成算法,能快速、准确设计出贯穿正交机织物组织矩阵,从而提高该类三维纺织复合材料增强体结构的设计效率。
复合材料;贯穿正交机织物;交织规律;组织矩阵;生成算法
随着复合材料应用的不断增多,对其结构设计的研究越来越引起复合材料设计领域的重视。三维纺织复合材料是采用纺织技术将纤维加工成三维预型件的复合材料,其中正交机织物是三维纺织复合材料广泛采用的增强体结构之一,由于接结经纱对其他系统的纱线的固定作用,从而加强各层纱线间的联系,使材料整体具有优异的抗分层、抗冲击能力[1-3]。结构设计及其性能研究一直是复合材料设计的热点之一。Legrand等[4]从宏观和微观两个角度分别分析了三维机织物在模具约束作用下织物结构的变化。Lomov等[5]提出一种采用编码来表示三维复合材料结构的方法,并结合给定经纬纱的几何和力学参数计算出织物中所有纱线的空间位置。丁辛等[6]提出三维机织几何结构数值表征的普适方法,定义了接结深度,接结长度等9个结构参数及其关系。聂建斌等[7]针对多层机织物的交织规律提出子组织概念,建立了新的多层的组织图绘制方法。臧海迪等[8]提出一种多层正交织物整体结构的快速设计方法。上述研究表明三维机织物交织规律比一般织物复杂,本文以提高三维纺织复合材料增强体结构设计效率为目的,通过对贯穿正交织物交织规律的分析,建立了矩阵模型,并提出了矩阵列向量元素之间关系及其赋值算法,为提高其设计效率提供了有价值的参考。
1 贯穿正交机织物交织规律
正交机织物由纬纱、地经纱、接结纱三组纱线交织而成,接结纱贯穿全部厚度时,即为贯穿正交。若接结纱沿经向引入,则称为接结经正交。若接结纱沿纬向引入,则称为接结纬正交。接结经正交机织物,纬纱比经纱多一层,接结纬正交机织物经纱比纬纱多一层。

图1 贯穿正交机织物立体结构图
图1为3层纬纱的接结经贯穿正交机织物,向纱为地经纱,向纱为纬纱,向纱为接结经。地经纱和纬纱呈直线状态,分别沿经、纬向交替排列。接结纱沿向依次穿过所有经纬纱层,并往复形成交织循环。依靠接结纱的固结作用,形成稳定的结构。
为了便于分析,贯穿正交机织物交织可用图2(a)交织示意图和图2(b)组织图简化表达,并作如下约定:
(1)圆圈代表纬纱,圆弧和直线组合线、水平线分别代表接结经纱、地经纱。
(2)圆圈行代表纬纱层,圆圈内数字为纬纱序号,左侧数字代表接结经及地纱纱序号,以便分析交织规律。

图2 贯穿正交机织物交织示意图和组织图
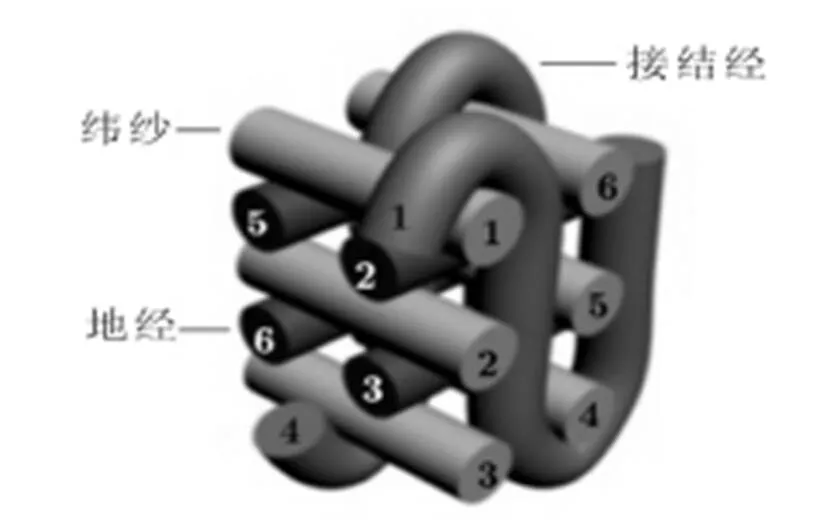
图3 贯穿正交机织物结构单元
正则贯穿正交机织物具有规则结构,当组织参数确定后,其组织图也随之确定。通过分析图2(a)所示的交织示意图,可得到图2(b)所示的组织图。图2(b)中接结经纱与纬纱交织的经组织点用“×”表示,地经纱与纬纱交织的经组织点用“■”表示,纬组织点用“□”表示。
为了分析交织规律,以图3所示的纬纱3层贯穿正交机织物的一个结构单元分析。由图3可知,一个结构单元由6根纬纱、4根地经纱和2根接结经纱构成。分别对经、纬纱进行编号,其中1、4号经纱为接结经,2、3、5、6为地经。
织第1纬时经纱1提升,织第2纬时经纱1、2、5提升,织第3纬时经纱1、2、3、5、6提升,织第4纬时经纱2、3、4、5、6提升,织第5纬时经纱2、4、5提升,织第6纬时经纱4提升。
通过上述分析,令纬纱层数为,完全组织经、纬纱数分别为R、R,接结经纱间经向飞数S,则R,R,S分别满足式(1)、(2)、(3)。
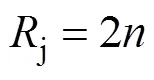
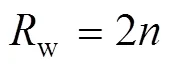
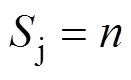
2 贯穿正交矩阵模型及生成算法
根据贯穿正交机织物交织特点,可构建矩阵来表达交织规律[9,10],如式(4)。矩阵的参数包括行数、列数和代表组织点性质的元素a,其中r=R、c=R。为区别接结经纱和地经纱,用“1”、“0”分别表示接结经纱与纬纱交织形成的经、纬组织点,“3”、“2”分别表示地经纱与纬纱交织形成的经、纬组织点。
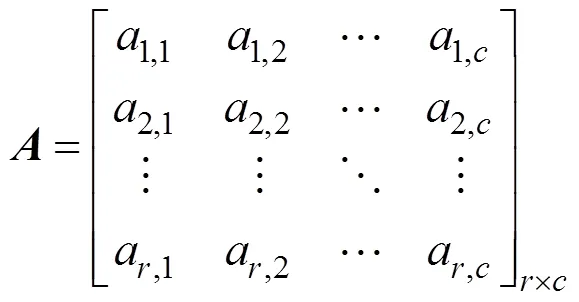
由图2(b)所示的组织图发现,整个组织图可分为接结经与纬纱交织的部分,以及地经纱与纬纱交织的部分形成。令整个矩阵为,其列数c=R、行数r=R,分别按式(1)、(2)确定。将矩阵分为1个接结经纱矩阵1和2个地经纱矩阵2。矩阵1的列向量表示接结经纱,分别用“1”、“0”代表经、纬组织点。矩阵2的列向量表示地经纱,分别用“3”、“2”代表经、纬组织点。其中矩阵1的行数1、列数1,分别为22。矩阵2的行数2、列数2,分别为2,-1。
贯穿正交组织矩阵等价于2个矩阵2嵌入1个矩阵1的列向量之间,具体生成算法包括以下3个步骤。
(1)生成接结纱矩阵1
对矩阵1的第1、2列元素a1赋值,可分别根据式(5)、(6)进行。

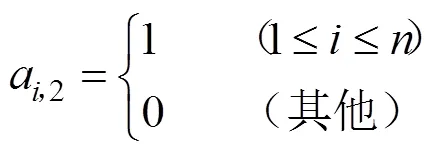
式中=1,2,…,2;表示纬纱层数。
(2)生成地经纱矩阵2
根据图2地经与纬纱交织具有上下对称性的特点,元素a中的取值范围是1到-1,的取值范围可分为两段,1到,+1到2,分别用式(7)、(8)赋值。

(8)
(3)生成贯穿正交矩阵
根据接结经纱矩阵1和地经纱矩阵2,按照式(9)的方式嵌入,建立矩阵。


图4 纬纱4层贯穿正交机织物组织图
3 矩阵生成算法验证
以图5所示的纬纱4层接结经贯穿正交机织物组织图为例,验证其矩阵生成算法。
(1)生成接结经纱矩阵1
由图4,纬纱层数=4,得到R=8,R=8,S=4,其中接结经纱矩阵1的行数1=8,列数1=2。由式(5)、(6)依次带入=1,2,…,8得矩阵1,如式(10)。

(2)生成地经纱矩阵2
图4左侧部分地经,由纬纱层数=4,地经纱矩阵2的行数2=8,列数2=3。矩阵2上半部分按照式(7),=1时,取1时11=2;取2,3,4时2, 1=3,31=3,41=3;=2时,取1,2时1, 2=2;2, 2=2;取3,4时3, 2=3,42=3。=3时,取1、2、3时1, 3=2,2, 3=2,3, 3=2,取4时43=3。
矩阵2的下半部分按照式(8),换算得出,最终得到地经纱矩阵2,如式(11)。

(3)生成贯穿正交矩阵
由图4,先将1个接结经纱矩阵1放入矩阵,再将2个地经纱矩阵2放入矩阵。由式(9),=4,分别为1,2时,分别为1,5,即矩阵的第1、5列分别等于矩阵1的第1、2列,完成接结经纱矩阵1嵌入矩阵。

通过验证图4及式(12)表明,给出的贯穿正交机织物矩阵生成算法正确无误。
4 结 论
(1)分析了贯穿正交机织物的交织规律,并建立了其矩阵模型。
(2)建立了接结经纱矩阵、地经纱矩阵赋值算法及嵌入算法。
(3)该方法能快速、准确的实现贯穿正交机织物矩阵的建立,从而提高其设计效率。
[1] 冯兆行, 田伟, 马雷雷, 等. 三维机织正交结构复合材料的参数化设计[J]. 纺织学报, 2010, 31(12): 59-63.
[2] 徐艺榕, 孙颖, 韩朝锋, 等. 复合材料用三维机织物成型性的研究进展[J]. 纺织学报, 2014, 35(09): 165-172.
[3] 易洪雷, 丁辛. 三维机织复合材料力学性能研究进展[J]. 力学进展, 2001, 31(02): 161-171.
[4] Xavier Legrand, François Boussu, Saad Nauman,et al. Forming behaviour of warp interlock composite[J]. International Journal of Material Forming, 2009, 22 (1): 177-180.
[5] S.V. Lomov, A.V. Gusakov, G. Huysmans, et al. Textile geometry preprocessor for meso-mechanical models of woven composites[J]. Composites Science and Technology, 2000, 60(11).
[6] 丁辛, 易洪雷. 三维机织几何结构的数值表征[J]. 东华大学学报(自然科学版), 2003, (03): 15-19.
[7] 聂建斌, 何奕中. 多层机织物的组织设计[J]. 纺织学报, 2010, 31(02): 50-53.
[8] 臧海迪, 陈涛, 白燕. 多层正交织物的快速设计[J]. 上海纺织科技, 2014, 42(04): 30-32.
[9] 王旭. 机织物组织结构的三维建模方法研究[J]. 河南工程学院学报(自然科学版), 2013, 25(01): 6-10.
[10]朱建华, 张瑞云, 王伟, 等. 复杂组织多层机织物三维建模与仿真[J]. 玻璃钢/复合材料, 2016, (02): 47-52.
Matrix Model of 3D Textile Composites Reinforcement Structure
DU Zeng-feng1, WANG Xu1,2, LIU Xin-hua1,2
(1.College of Textile and Clothing,Anhui Polytechnic University, Wuhu Anhui 241000, China; 2. Science and Technology Public Service Platform for Textile industry, Anhui Polytechnic University, Wuhu Anhui 241000, China)
In order to improve the design efficiency of the three-dimensional textile composite reinforcement structure, taking the through-thickness orthogonal woven fabric as an example, a matrix model was proposed on the basis of analyzing the interlacing rule, and the generation algorithm of matrix was given too. The column vectors and row vectors of the matrix model represent the warp and weft respectively, and then the warp float points and the weft float points of bind-warp were respectively represented with "1" and "0", while the warp float points and weft float points of ground-warp were respectively represented with "3" and "2" in matrix model. The corresponding relation of elements between column vectors of matrix and the algorithm of matrix generation were established. The results show that the proposed matrix model and its generating algorithm can quickly and accurately design the matrix of through-thickness orthogonal woven fabric and improve the design efficiency of this kind of 3D woven fabric.
composite material;through-thickness orthogonal woven fabric;interlacing rule;weave matrix;generation algorithm
王旭(1973-),男,副教授,博士,研究方向:三维纺织复合材料结构设计.
安徽工程大学研究生实践与创新资助项目(2017);安徽高校优秀青年骨干人才访学研修项目(gxfx2017045);安徽工程大学国家自然基金预研项目(2013).
TS106.6
A
2095-414X(2018)06-0021-04
