一种改善PMSS弱磁电流稳定性的控制策略

单文桃, 王 鑫

(江苏理工学院 机械工程学院，江苏 常州 213001)

高精度、高转速数控机床是实现高速加工技术的基础，而高速电主轴单元是高精度、高效率高档数控机床的核心功能部件之一，是航空航天、汽车、船舶、精密模具、精密机械等尖端产品制造领域所需高档加工母机的核心部件。永磁同步电主轴(Permanent Magnet Synchronous Spindle,PMSS)是高速电主轴单元种类之一，其具有以下几个优点：① 转子不发热。因为PMSS采用永磁体励磁，运行过程中无励磁损耗，故转子不发热；② 功率密度高、易启停。由于钕铁硼等高磁场强度永磁体材料的应用，电主轴的体积和重量大为减小，因此PMSS转动惯量小，易于快速启停；③ 功率因数高。转子转速严格与电源同步，工作效率高。

高速电主轴作为高速机床的核心部件，同时也是该类机床的主要热源。随着切削进给速度和加速度加大，机床的发热量将急剧增加。对于高速机床来说，热变形所引起的加工误差可占总体误差的30%～70%，PMSS的转子由永磁体构成，与三相异步电主轴相比，其转子在转动时不发热，能够减小热变形所引起的加工误差，有利于高精度、高转速的加工。PMSS高速化是未来数控系统发展的主要趋势之一，由于受到逆变器容量地限制，电主轴要获得较宽的调速范围并且高速时具有较稳定的定子电流，就存在一定的困难，解决这些困难是目前弱磁控制研究主要的研究方向。弱磁控制技术可使PMSS在低速时获得恒定转矩，以适应大转矩启动的要求；在高速时输出恒定功率，进一步提高电主轴的运行速度，拓宽调速范围。

针对PMSS的弱磁控制策略，国内外学者提出了诸多弱磁控制方案和改进措施。文献[1]提出了六步电压法，最大化利用直流母线电压，但该方法无法准确估算定子磁链，进而影响系统准确性和动态性能。文献[2-3]提出了电流调节器法，该方法鲁棒性好，但改变转速和转矩时最优直轴电压难以比较。文献[4]提出了自适应反演控制，该方法有很好的抗干扰性能力及较强的鲁棒性，但自适应模型地建立及内部参数地整定难度较大。文献[5-7]提出了超前角弱磁控制算法，该方法不依赖电机参数，计算较方便，且易于实现，但传统超前角弱磁控制算法存在电流震荡的问题。

模糊理论由自动控制理论专家L.A.Zade最先提出。1974年，英国的Mamdani首先把模糊理论用于工业控制，取得了良好的效果[8]。模糊控制系统的鲁棒性强，干扰和参数变化对控制效果的影响被大大减弱，尤其适合非线性、时变及纯滞后系统地控制。由于PMSS具有强耦合及强非线性的特点，因此在PMSS上应用模糊控制会取得良好的效果。

鉴于此，本文针对PMSS弱磁调速时定子电流震荡的现象，提出了一种基于模糊控制的改进型超前角弱磁控制策略。利用MATLAB中已有的Fuzzy-Logic Toolbox，进行模糊参数地设定，使用模糊控制器代替原有超前角弱磁控制模型中的转速PI调节器，并在弱磁环中使用变积分调节器。经过MATLAB仿真，模拟出基于模糊控制的改进型超前角弱磁控制策略的运行状态，并细致地分析了电主轴的运行状态，验证了该方法的正确性和有效性。

1 永磁同步电主轴数学模型

本文提到的表贴式永磁同步电主轴d-q轴系下定子电压方程[9]为

(1)

式中：ud和uq为d轴、q轴的定子电压；id和iq为d轴和q轴的定子电流；Ld和Lq为d轴、q轴的等效电感；Ls为定子电感；Rs为定子相电阻；ωr为转子电角速度；ψf为转子永磁体产生的励磁磁场的基波磁链。

在电主轴高速稳定运行时，可忽略定子压降，电压方程可改写为

(2)

PMSS的电磁转矩Te方程为

(3)

式中：Pn为极对数；β为定子三相基波合成磁动势轴线与永磁体基波磁动势轴线间的空间电角度，称为转矩角。

由于逆变器容量地限制，电压矢量必然存在一个最大值ulim，满足：

(4)

式中:us为定子电压。

电流矢量同样也受到一定地限制，存在一个最大值ilim，满足：

(5)

式中：is为定子电流。

2 模糊控制的改进型超前角弱磁调速策略

2.1 PMSS超前角弱磁调速原理

由PMSS的数学模型可知，随着电主轴转速升高，其产生的反电势也会增大。当电主轴运行在基速以上时，电主轴定子电枢的反电势等于逆变器自身能输出的最大极限值，因此在受到逆变器直流侧电压最大值地限制时，继续通过调整直流侧电压获得更高的转速已经不太可能，这时需要对电主轴进行弱磁控制，以此达到扩速的目的。PMSS弱磁控制的思想来自他励直流电动机的励磁控制。他励直流电动机的端电压随转速升高而升高，当端电压达到极限值时，若继续升速，必须降低电机的励磁电流，使磁场减弱，才能保证反电势和电压的平衡。

首先定义定子电流矢量is在d-q轴系下，超前于q轴的电角度为电流超前角，简称超前角γ，电流超前角,如图1所示。

受到逆变器容量地限制，PMSS稳定运行时，电压矢量满足式(4)。忽略定子压降后，将式(2)代入式(4)可得

(6)

由式(4)和式(5)所描述的电压和电流轨迹绘制得到，同时因d轴、q轴的等效电感Ld和Lq相等，故电压轨迹为圆，电压、电流极限圆,如图2所示。

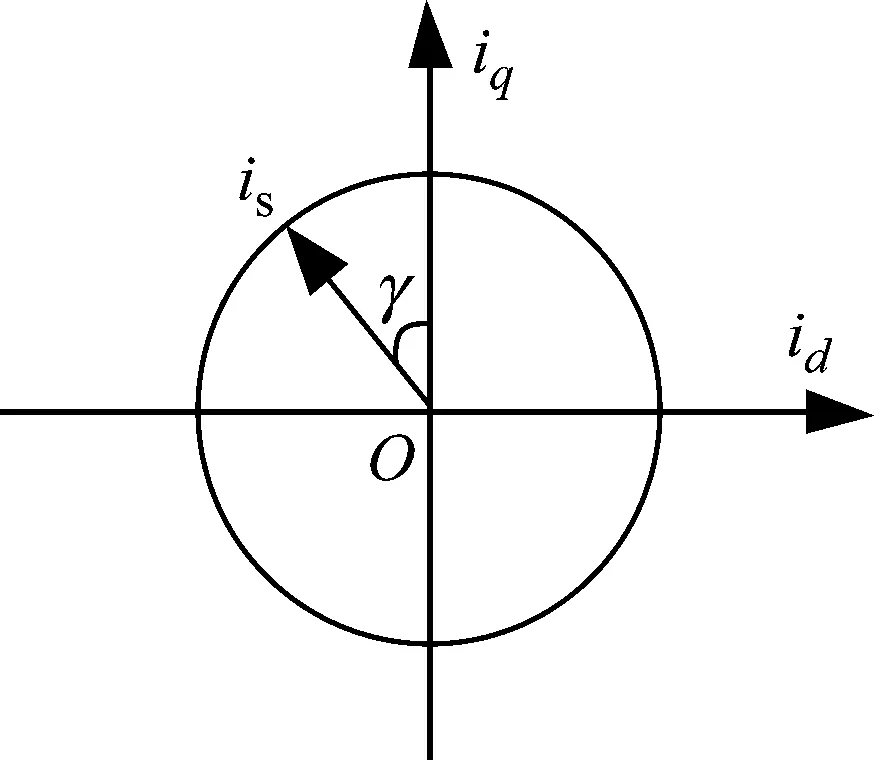
图1 电流超前角Fig.1 Current leading angle

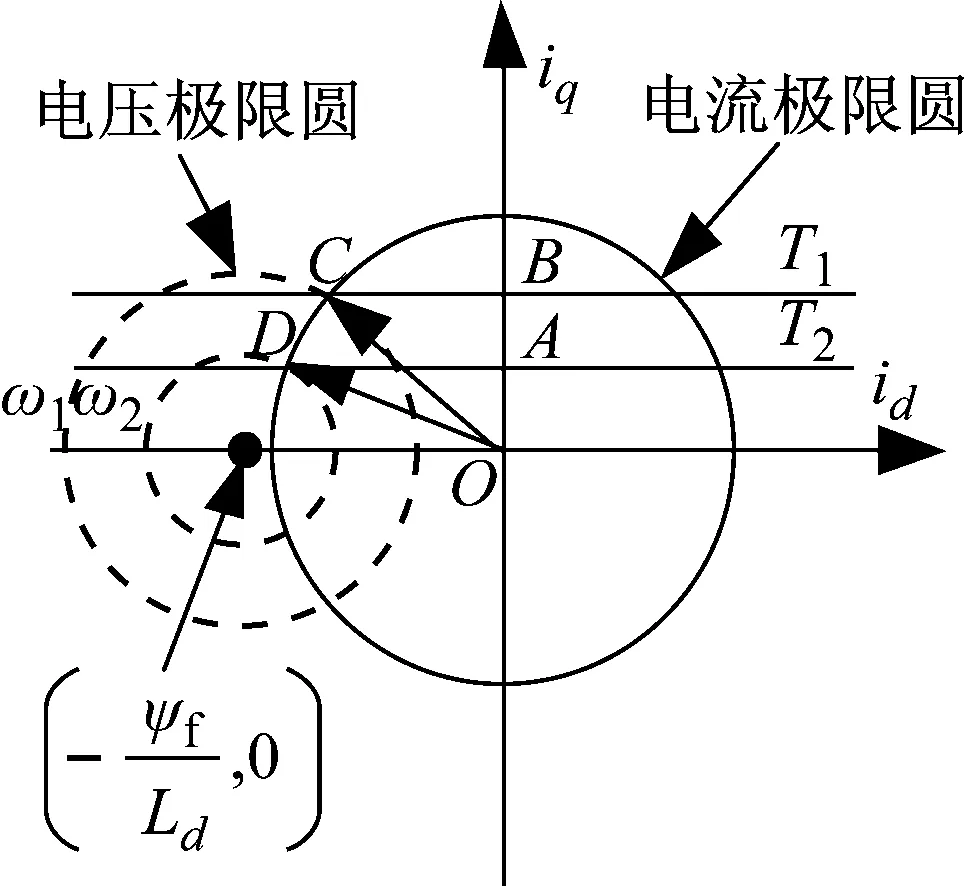
图2 电压极限圆与电流极限圆Fig.2 Voltage limit circle and current limit circle

通过图2可分析PMSS的弱磁过程，在基速以下时，采用id=0的矢量控制策略，定子电流is全部用来产生交轴定子电流iq，此时超前角γ=0，若负载转矩为T2，则电流轨迹为O→A。当转速超过转折速度时，逆变器输出容量已达到最大值，无法再继续提供升速所需的电压，此时只能依靠弱磁的方式来升速，即增大直轴电流分量id，以此削弱转子永磁体所产生的气隙磁通，此时超前角γ开始逐渐增大，速度达到ω2时，电流轨迹为A→D。同理，当负载转矩为T1(T1>T2)时，速度稳定到ω1时，整个电流运动轨迹为O→B→C。弱磁的同时也要减小交轴电流分量iq以维持电压平衡，从而使电主轴转速ωr升高，达到弱磁升速的目的。

2.2 改进型弱磁调速策略的提出

在转折速度以下时，PMSS工作在恒转矩区，未进入弱磁区，随着转速地升高，电主轴的定子端电压也不断升高，电流PI调节器的输出逐渐趋近饱和。当到达转折速度时，电流PI调节器饱和，电主轴的定子端电压达到逆变器输出的最高电压，此时通过增大id来提高转速，但在电主轴达到给定转速时，定子电流将出现震荡现象。

为提高PMSS弱磁稳定性，抑制定子电流震荡现象，本文提出了基于模糊控制的改进型超前角弱磁控制策略，系统结构,如图3所示。控制策略中以电流环的输出值ud、uq作为弱磁环的输入信号，其平方和的开方值us与给定电压Umax之间的差值作为变积分调节器的输入，当us低于Umax时，变积分调节器正向饱和，超前角γ输出为0；当us高于Umax时，调节器根据差值大小调节积分增益Ki，在差值过大时减小Ki，差值较小时增大Ki，以此抑制定子电流因积分饱和而发生震荡。同时使用模糊PI调节器对转速误差ne进行控制，根据转速误差ne大小动态调节参数，为弱磁环的输入提供更优的目标值，解决因传统PI调节器参数不可调导致系统稳定性变差的问题。

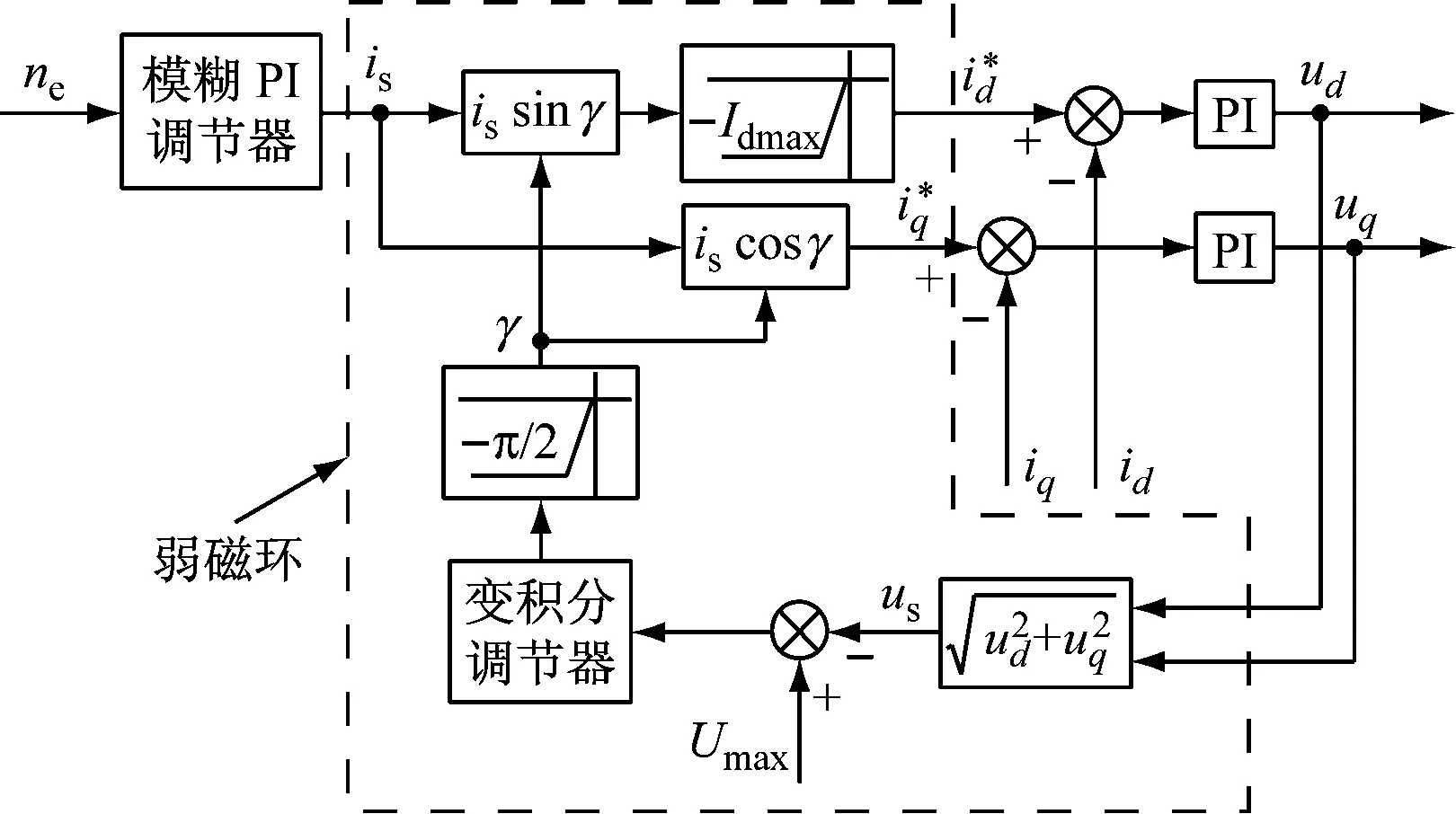
图3 改进型超前角弱磁控制结构框图

此方案克服了系统运行过程中因弱磁调节器与转速调节器参数不可调对系统所造成的影响，使系统获得较好的稳定性和控制效果。

3 电主轴模糊PI调节器地设计

在模糊PI调节器地设计过程中，由于操作者经验难以描述，控制对象过程及其参数复杂多变，故引入模糊理论来解决这一难题。通过采用模糊数学的基本理论，把规则的条件和操作用模糊集表示，并把这些模糊控制规则、有关评价指标以及初始PI参数等信息作为知识存入计算机知识库中，计算机再根据系统的响应情况，运用模糊推理，即可自动实现对PI参数的最佳调整[10-11]，模糊自适应PI控制结构,如图4所示。

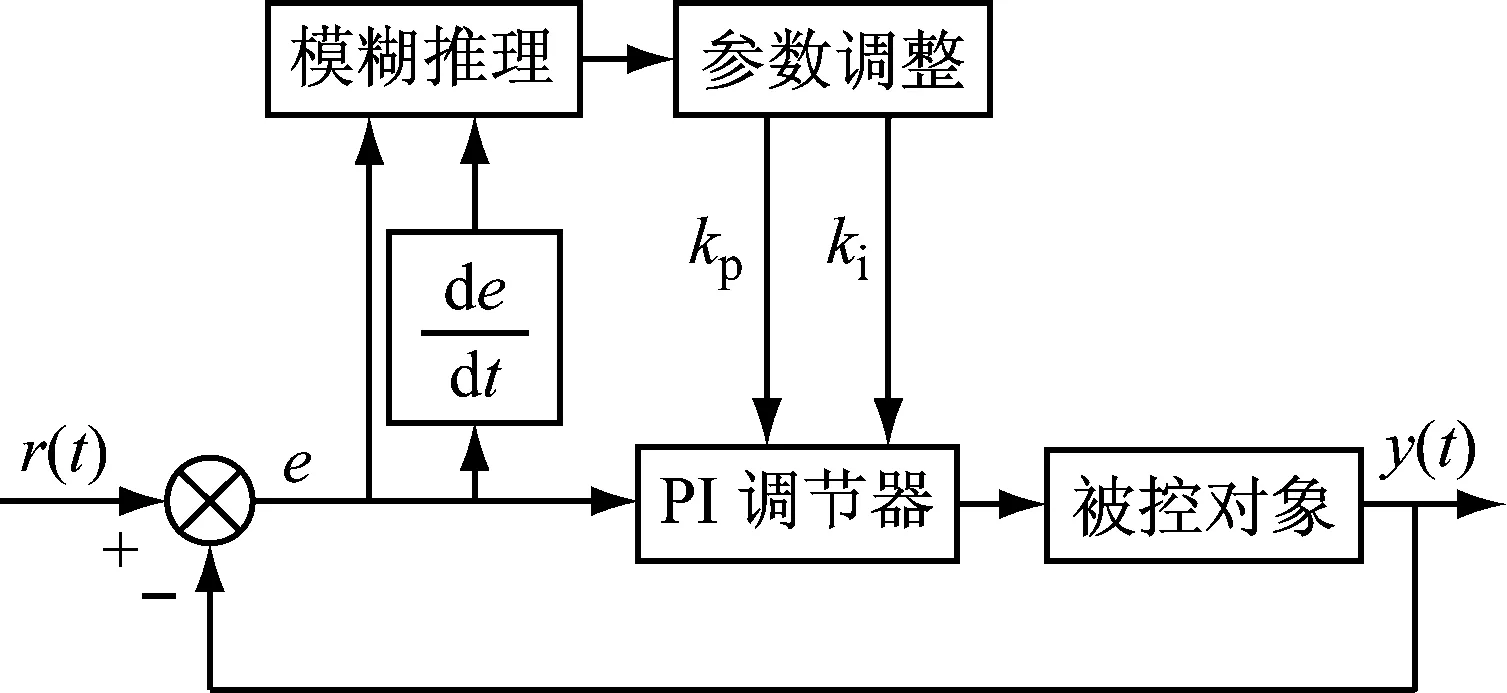
图4 模糊自适应PI控制器结构框图

3.1 隶属度函数与模糊逻辑决策的确立

模糊化处理是将精确的输入量和控制输出量模糊化。将电主轴转速的实测值与给定值的瞬时误差e及其误差变化ec作为输入变量，令其量化等级为7级，即{-3,-2,-1,0,1,2,3}，瞬时误差e的论域为[-10 000,10 000]，其误差变化ec的论域为[-150 000,150 000]，均服从三角型隶属度函数分布曲线。以PI调节器的Δkp、Δki两个参数作为输出变量，量化等级为7级，即{-3,-2,-1,0,1,2,3}，Δkp输出的论域为[-2,2]，Δki输出的论域为[-1,1]，均服从三角形隶属函数分布曲线，各输入输出的模糊子集均为{NB,NM,NS,Z,PS,PM,PB}，转速瞬时误差e、其误差变化ec和Δkp的隶属度函数,如图5所示。Δki的隶属度函数,如图6所示。模糊集的隶属度函数如表1所示。

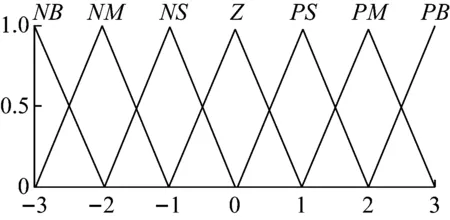
图5 e、ec和Δkp的隶属度函数图

模糊逻辑决策采用Mamdani算法的max-min进行合成，取误差e和误差变化ec的模糊集进行直积运算，其结果再和模糊算子进行模糊矢量积运算得出系统的控制输出量。

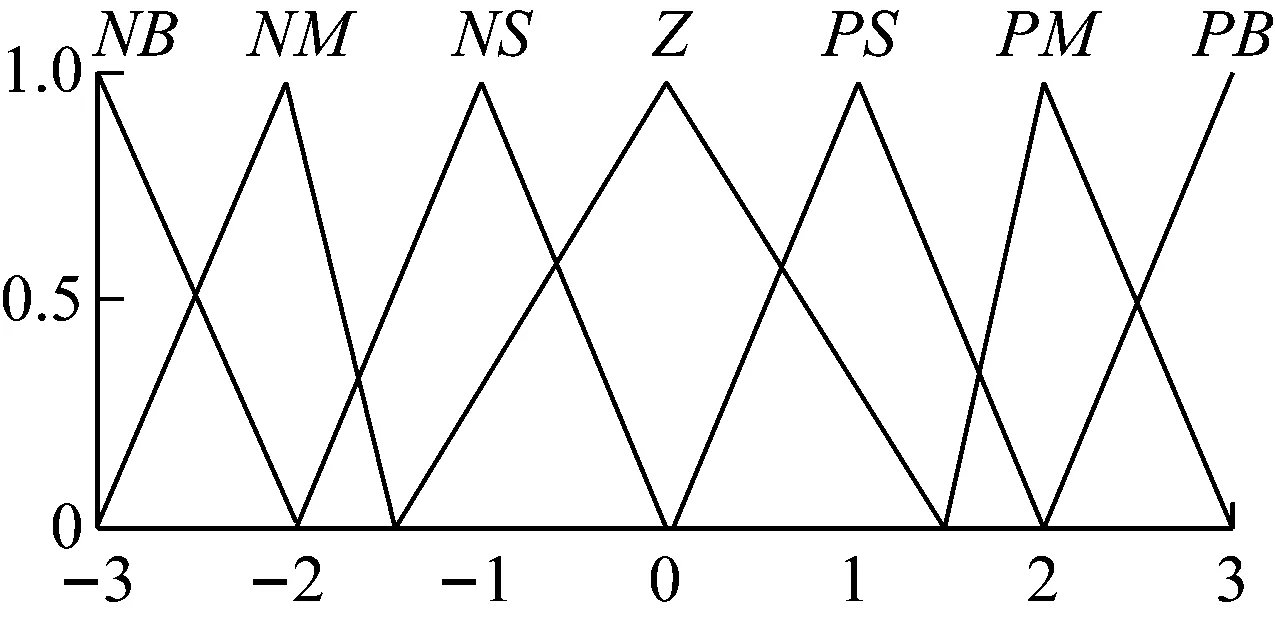
图6 Δki隶属度函数图

e×104ec×104ΔkpΔki量化等级-1-15-2-1-3-0.67-10-1.33-0.67-2-0.33-5-0.67-0.33-1000000.3350.670.3310.67101.330.672115213

3.2 控制规则的确立

比例系数kp成比例的反映控制系统的误差信号e，误差一旦产生，控制器立即产生控制作用，以减少误差。积分系数ki主要用于消除静差，提高系统的无差度。积分作用的强弱取决于积分时间常数。kp、ki的取值必须合适，若kp取值过大，会使系统产生超调；取值过小则减缓了系统的响应速度。若ki取值过大，将会因积分饱和引起较大超调，过小则无法消除静差，控制精度受到限制。参数整定时，必须考虑到在不同时刻两个参数的作用以及相互之间的联系。模糊自适应PI调节器通过计算当前系统误差e和误差变化率ec，利用模糊规则进行模糊推理，查询模糊矩阵表进行参数调整[12-14]，Δkp整定的模糊规则表,如表2所示。Δki整定的模糊规则表,如表3所示。

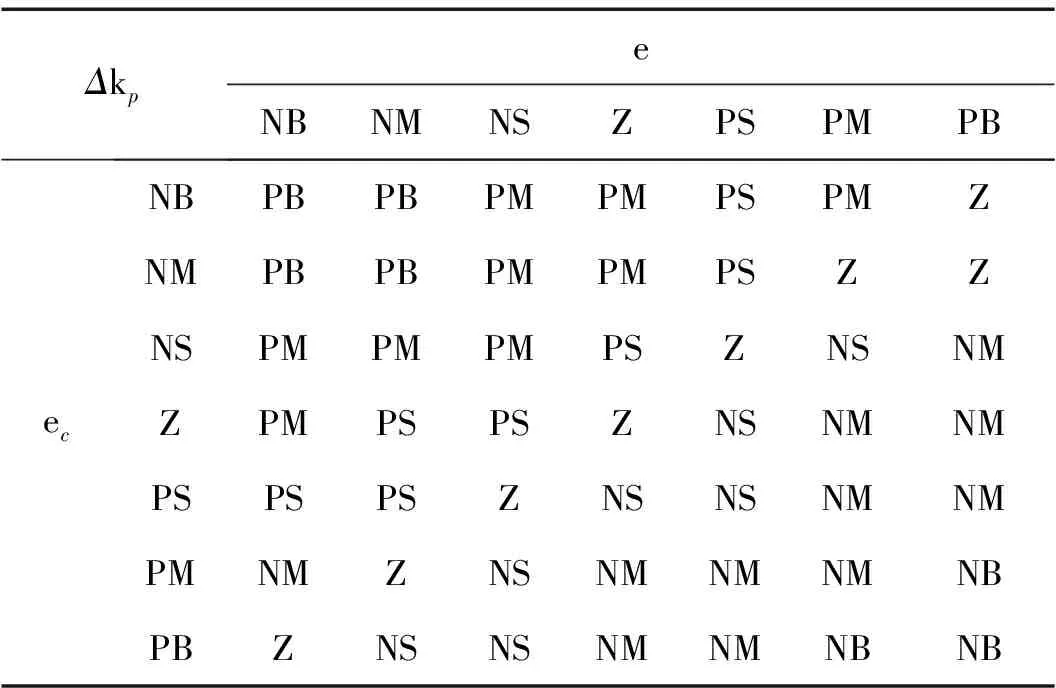
表2 Δkp的模糊规则表

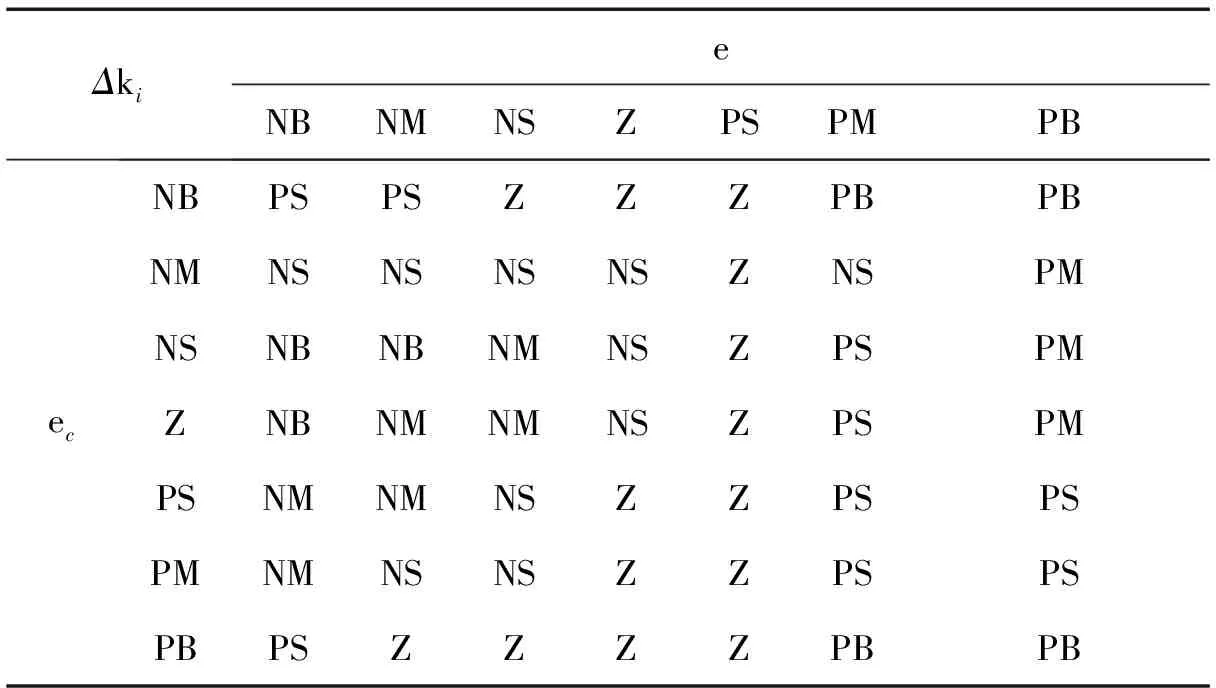
表3 Δki的模糊规则表

3.3 模糊量反模糊化

在模糊控制中，常用的两种反模糊化方法为最大隶属度法和重心法。本文采用输出更加平滑的重心法，重心法是取模糊隶属度函数曲线与横坐标围成面积的重心模糊推理得最终输出值，其表达式为[15]

(7)

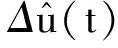
4 电主轴弱磁控制系统MATLAB/Simulink仿真验证

在MATLAB环境下，采用Simulink和Simscape的块图模型建立永磁同步电主轴控制系统的仿真模型。采用本文提出的基于模糊控制的改进型超前角弱磁控制策略进行弱磁控制，电主轴和实验的参数,如表4所示。

表4 永磁同步电主轴模型和实验参数

4.1 实验一：弱磁扩速

本实验的主要目的是将本文所提出的模糊控制改进型弱磁调速策略与普通id=0的控制方法进行对比，来验证此弱磁策略的调速性能。

无弱磁调速的转速图,如图7所示。此实验中，仿真时间为1 s。在t=0 s时，电主轴空载启动运行，给定转速为10 000 r/min，电主轴在上升时间tr=0.12 s时刻达到额定转速3 100 r/min，之后维持此速度稳定运行，说明该方案在转速达到3 100 r/min时，电主轴在逆变器容量范围内已经无法再提高转速。

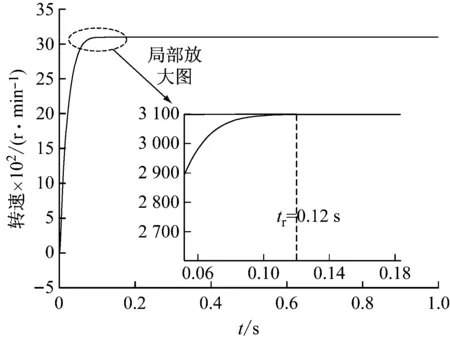
图7 id=0转速图

第二次进行了本文提出的改进型超前角弱磁调速策略的实验，弱磁调速的转速图,如图8所示。电主轴在tr=0.419 76 s时第一次达到给定转速，之后产生超调，在tp=0.427 9 s时达到转速峰值，并且此时的超调量σ%=0.78%，符合系统动态性能指标。

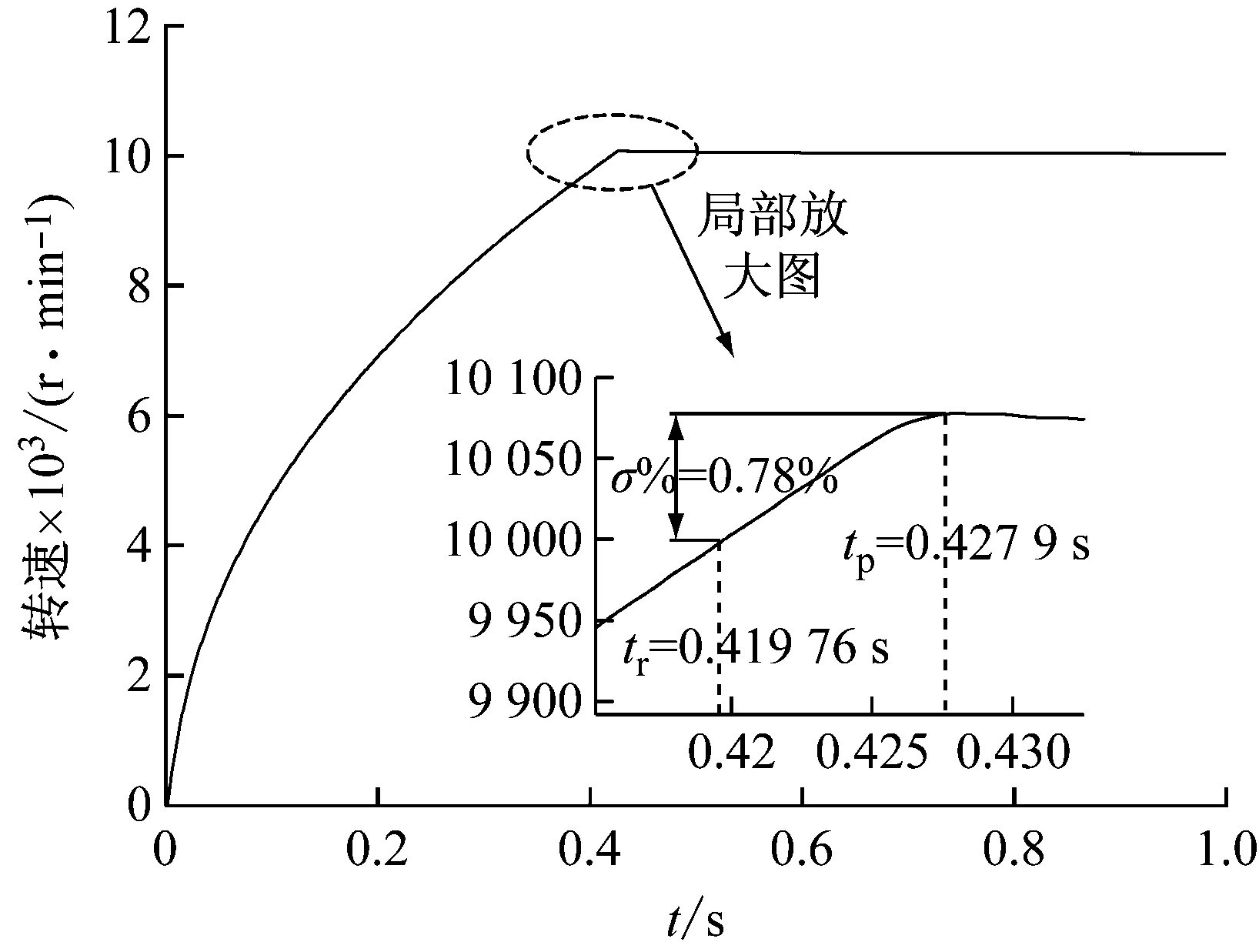
图8 弱磁调速转速图

此实验说明：无弱磁控制环节时，电主轴的运行速度范围有限，无法达到现场加工要求的转速。在加入弱磁环节后，电主轴的调速能力明显提升，达到弱磁扩速的目的，且系统的各个动态性能指标都较好。

4.2 实验二：定子电流稳定性实验

本实验的主要目的是将本文所提出的基于模糊控制的改进型超前角弱磁调速策略与传统超前角弱磁调速策略进行对比，来验证此改进型弱磁调速策略的优越性。

本文所提出的基于模糊控制的改进型超前角弱磁调速策略直轴定子电流,如图9所示。传统超前角弱磁调速策略直轴定子电流,如图10所示。两种策略均在t=0时，给定转速10 000 r/min，并在t=0.5 s时给定负载转矩2 N·m，两者对比可以明显地观察出，前者的直轴定子电流稳定性优于后者。同时，系统在t=0.5 s时加上负载，电流再次达到稳定后，前者的震荡幅值明显小于后者。

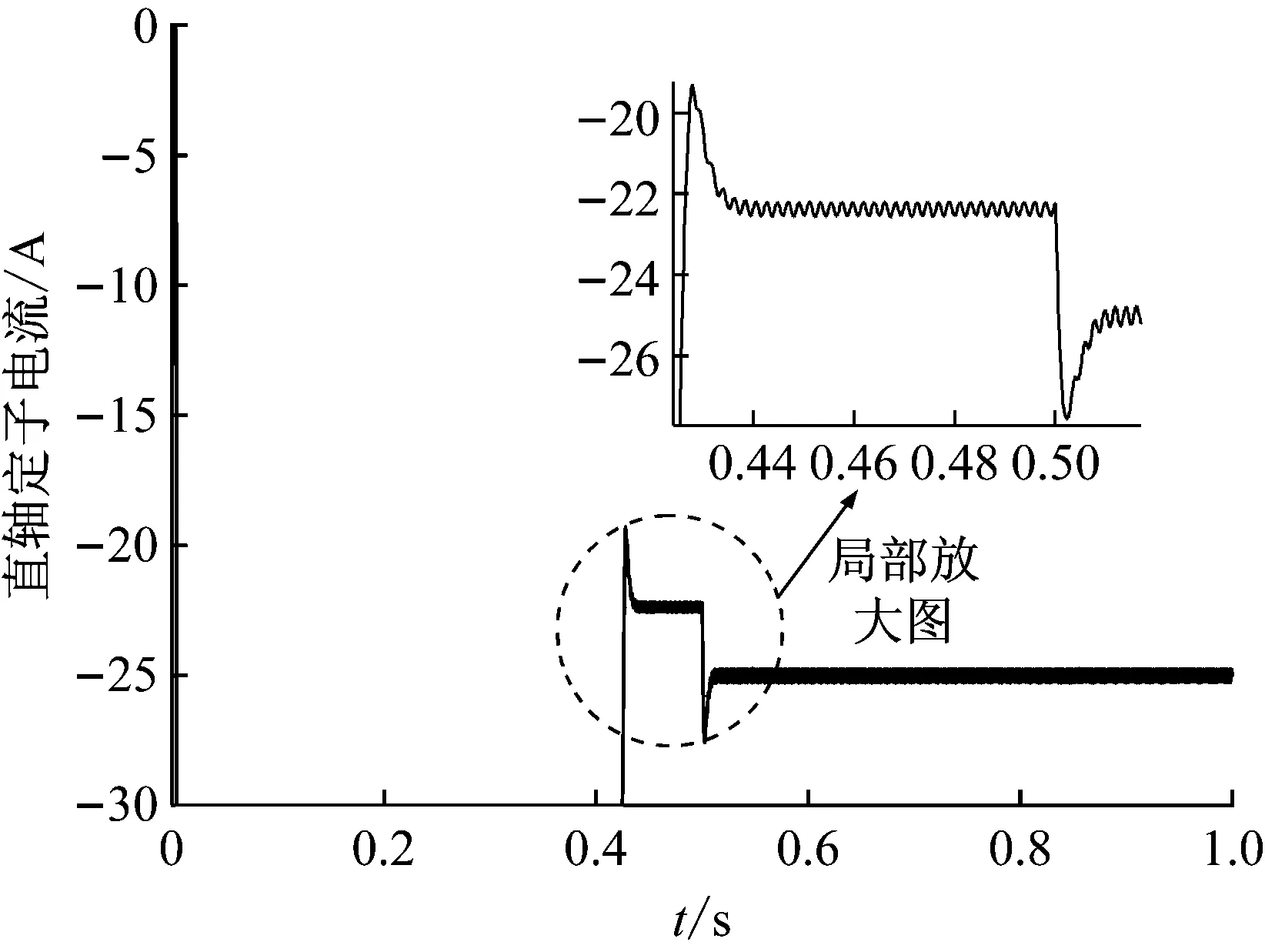
图9 改进型超前角弱磁控制直轴定子电流轨迹

Fig.9 Direct axis stator current trajectory of the improved leading angle flux-weakening control

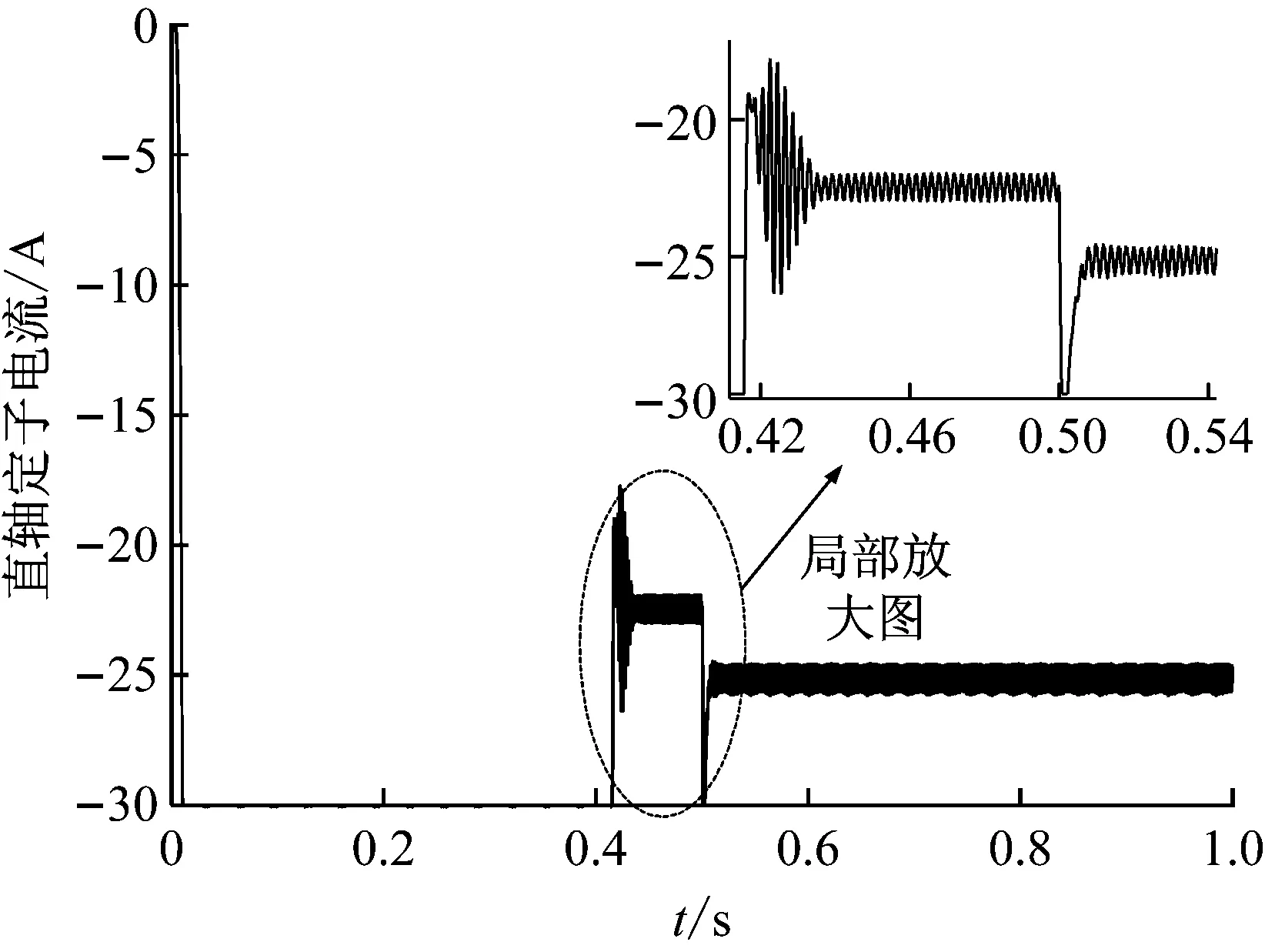
图10 传统超前角弱磁控制直轴定子电流轨迹

Fig.10 Direct axis stator current trajectory of the traditional leading angle flux-weakening control

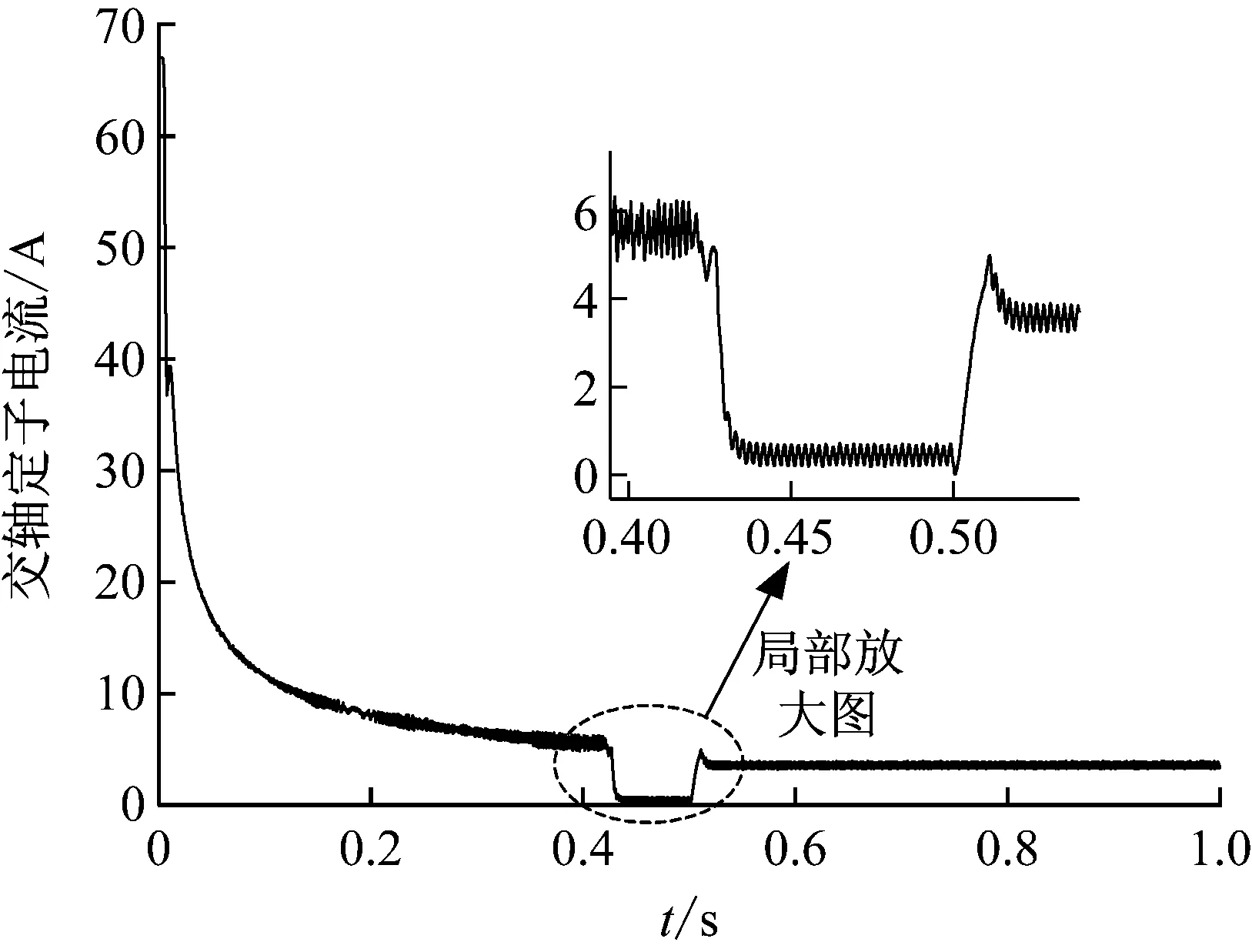
图11 改进型超前角弱磁控制交轴定子电流轨迹

Fig.11 Quadrature axis stator current trajectory of the improved leading angle flux-weakening control

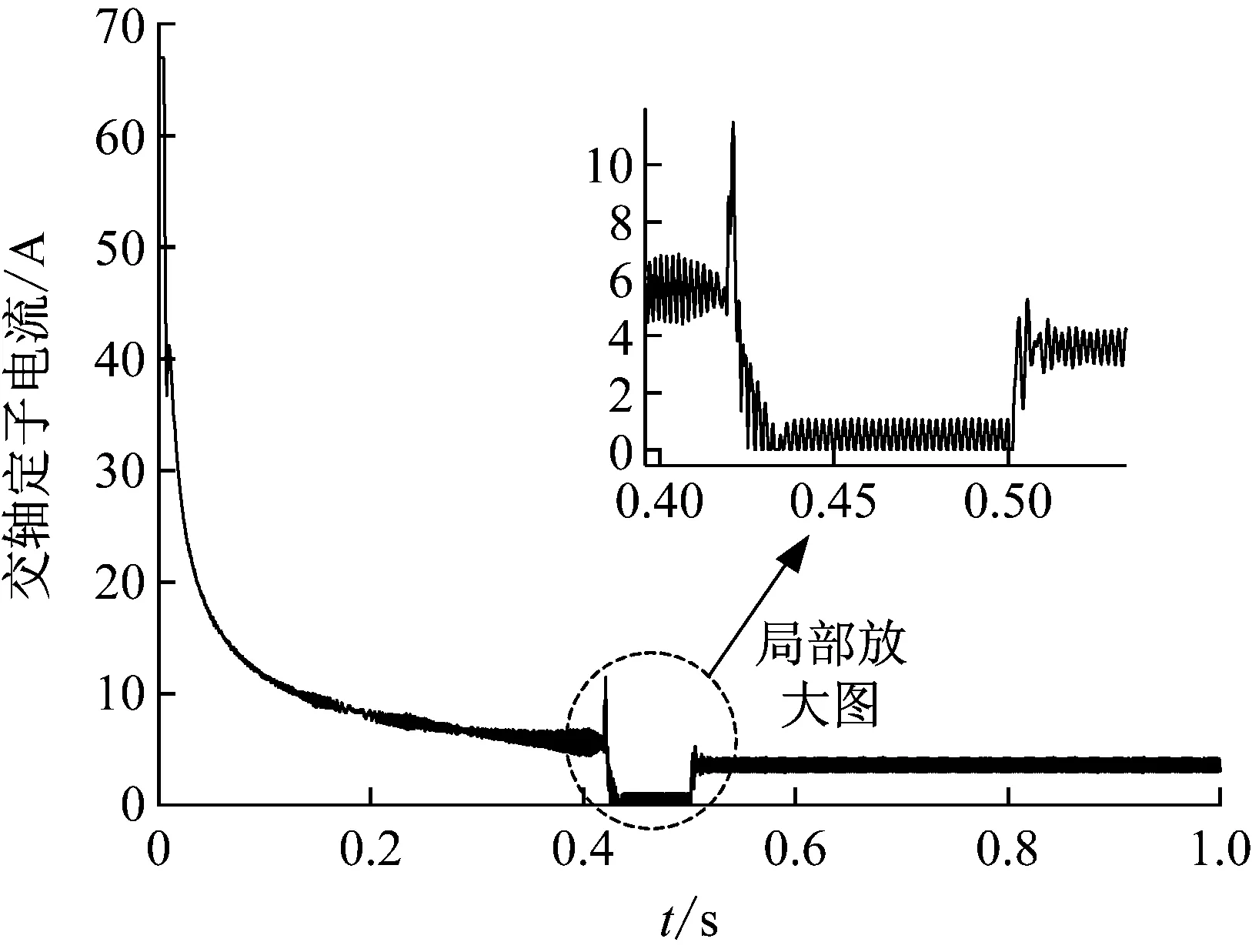
图12 传统超前角弱磁控制交轴定子电流轨迹

Fig.12 Quadrature axis stator current trajectory of the traditional leading angle flux-weakening control

本文所提出的基于模糊控制的改进型超前角弱磁调速策略交轴定子电流,如图11所示。传统超前角弱磁调速策略交轴定子电流,如图12所示。通过分析两个策略的交轴定子电流波形图可以看出，前者的波形轨迹整体都较平缓，具有较好的稳定性，而后者在加载前后，震荡幅值都大于前者。

此实验说明，本文提出的控制策略对交、直轴定子电流，无论是加载前还是加载后都具有较好地抑制震荡的能力，且变化趋势基本一致。此特点使系统整体的稳定性得到提高，并使高速加工性能更优更稳定。

5 结 论

本文针对永磁同步电主轴调速范围不足和定子电流震荡的现象，给出了一种基于模糊控制的改进型超前角弱磁调速策略。实验结果表明，采用该策略，电主轴在空载以及带负载的情况下能够进行深度弱磁，电主轴的转速从额定转速扩展了至少2倍，弱磁扩速的效果良好，同时在系统稳定性上，通过与传统控制策略的对比，证明其能较好地抑制定子电流震荡的现象，使得系统的稳定性得到显著提高，仿真结果证明了其正确性与有效性。