基于TR-PIV方法的格栅-空腔流动流场自激振荡空间特征研究
2018-12-21张永昌徐宇工
张永昌, 徐宇工
(1.内蒙古大学 交通学院,呼和浩特 010070;2.北京交通大学 机械与电子控制工程学院,北京 100044)
开放空腔流动是经典的流体力学问题之一,其示意图见图1(a)。一定条件下,开放空腔流场会形成自激振荡现象,造成流场速度、压力等物理量发生剧烈波动[1-2],继而引起结构承载、流致噪声等工程问题[3-4]。实际应用中,各类空腔结构的腔口处常安装有用以阻隔异物的格栅盖板。研究表明,流体流经具有格栅的空腔时同样有可能引发流场自激振荡现象[5],为方便描述,将该流动称为格栅-空腔流动,其示意图见图1(b)。尽管格栅-空腔流场自激振荡的产生方式及流场结构与开放空腔流场自激振荡不同,但其本质均属于剪切层自激振荡[6-8],具有很多相似的性质。
(a)
(b)
长期以来,为解决前述工程问题,国内外学者从不同角度对开放空腔流动进行了大量研究。其中,探究流场振荡空间分布规律一直是重要研究方向之一。很多研究均将其作为二维流动问题(x-y平面)进行处理[9-11],以归纳总结开放空腔壁面压力分布规律[12-15]为主。同时,一些学者对开放空腔流动的三维流动特性展开了研究[16-17]。相对于来流方向(x方向)和垂向(y方向),空腔展向(z方向)的流场振荡幅度较小。随着研究的深入,人们发现展向的流场振荡主要来自空腔内部环流,与流场自激振荡无关[18]。同时,空腔流动具有对称性,其对称面即为展向平分面[19-20]。
与开放空腔流动相比,针对格栅-空腔流动的研究起步较晚,以研究流场自激振荡的成因与变化规律为主。Celik等[21]的研究首次发现流体流经带有格栅或穿孔盖板的空腔时会激发流场自激振荡。Ozalp等[22]研究了穿孔板孔径对流场自激振荡的影响,并发现盖板外侧流场结构沿展向分布较为均匀,认为可以近似的将此类流动作为二维流动进行处理。针对该问题的后续研究[23-25]大多采用了该近似处理方法。因此,目前仍需对不同展向位置流动特征进行研究,从而加深对格栅-空腔流动流场自激振荡的空间分布特征的认识,明确不同空间位置流场振荡的时频特征,为格栅-空腔结构的设计研发及相关工程问题提供理论依据。如预测流动交变载荷的作用位置、强度、频率等。
根据上述研究背景,本文使用风洞实验方法,利用时间分辨粒子图像测速(TR-PIV)技术对格栅-空腔不可压缩流动进行测量,得到不同展向平面的流场速度分布。通过对不同空间位置速度波动频谱进行分析,明确流场自激振荡的空间分布特征。
1 实验方案
1.1 实验装置及设备
如图2所示,实验装置主要分为两部分,分别是箱体和格栅组件。箱体上部设计有凹槽,用以安装格栅组件。格栅组件由无色透明材料制成,从而满足激光透射和拍摄空腔内部流动的需求。同时,为消除散射的影响,将格栅除片状光源所在平面的部分涂为黑色。图中尺寸分别G=8 mm,H=8 mm,L=198 mm,W=400 mm。
实验在一座直流吹出式低速风洞上进行,其速度不稳定性、速度场不均匀性、湍流度均小于0.5%。使用TR-PIV系统进行测量。该系统采用高频双脉冲激光发生器输出波长为532 nm的激光。使用高速相机拍摄流场图像,相机分辨率为1 024×1 024像素,最大拍摄频率为500 kframe/s。使用癸二酸二辛酯油雾作为示踪粒子,其直径为1 μm左右。本实验使用的激光功率为5 325 W;激光照射时长为1×10-4s;激光脉冲间隔为3.5×10-3s;相机曝光时长为4×10-3s;相机延迟时长为1×10-4s;测量时长为20 s。
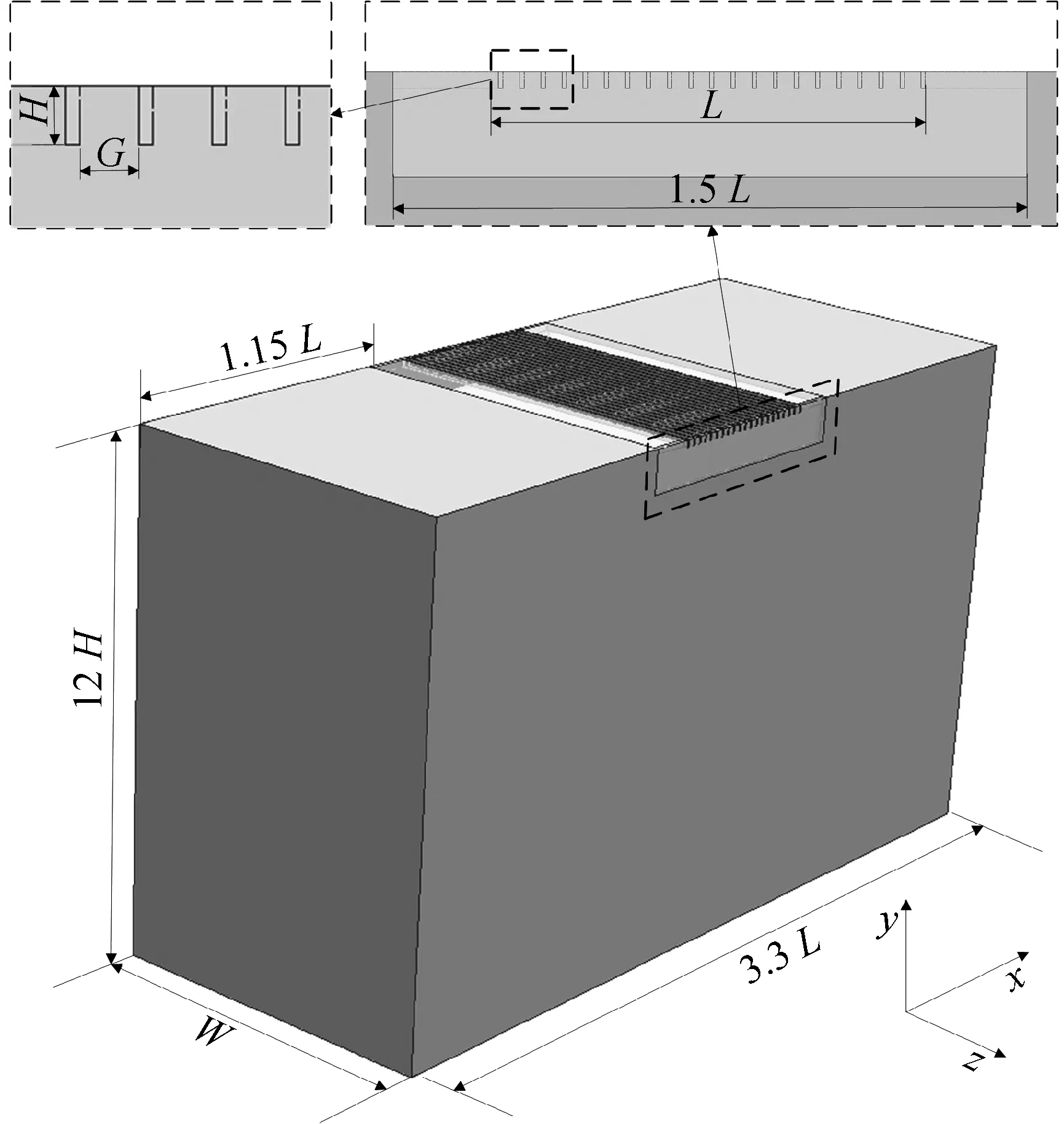
图2 实验装置示意图
实验装置及设备的布置方式,如图3所示。箱体及格栅组件安放在风洞内部。在空腔前部安装延长板,用以引导来流。激光发生器位于箱体及格栅组件的正上方,高速相机位于空腔侧面。
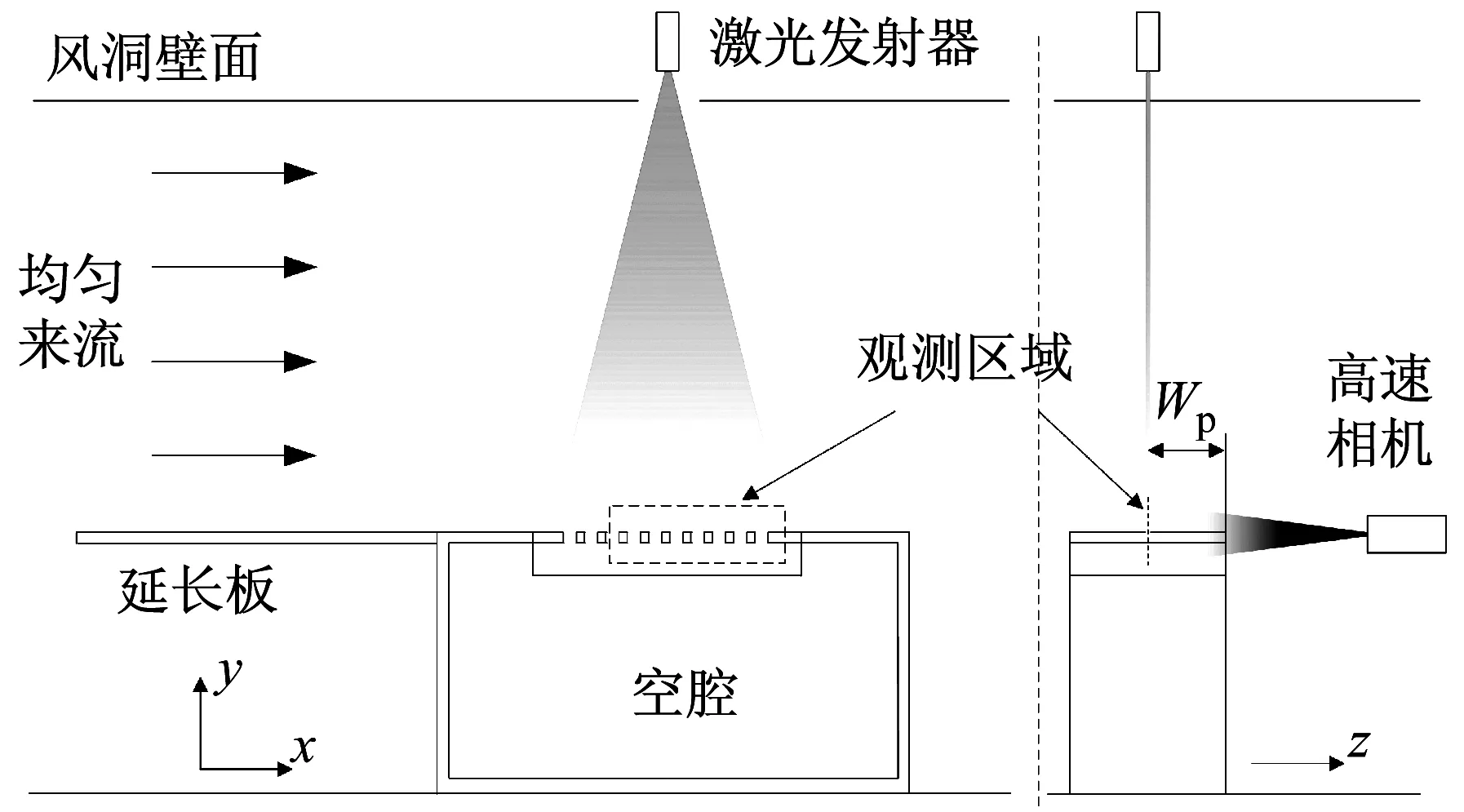
图3 实验设备布置
1.2 测量位置
实验时,激光发生器发射片状激光照亮x-y平面内随气流运动的示踪粒子,从而实现流场可视化。同时,高速相机记录该平面观测区域内的粒子图像。由于相机视野范围有限,观测区域不能完全覆盖格栅所在位置,故主要观测格栅中部及后部等流动情况复杂的重要区域(见图3),该区域的面积为164 mm×78 mm。
为研究流场自激振荡的空间分布规律,在不同展向位置分别设置多个测量平面,即片状激光所在平面。定义测量平面与靠近相机一侧的空腔壁面之间的距离为Wp(见图3右侧)。分别对Wp=0.125W,0.25W,0.375W和0.5W的几个平面进行测量。最后,通过对粒子图像进行处理得到不同时刻该平面的速度分布。
1.3 实验工况
实验工况主要由来流速度决定。在格栅-空腔几何参数确定的情况下,来流速度必须超过某一临界值才会激发流场自激振荡现象。同时,来流速度不可过小,否则会影响示踪粒子在流场中分布的均匀程度。根据以上两点需求,通过多次试验,最终确定对来流速度为10 m/s的工况进行研究。
1.4 实验数据处理
粒子图像拍摄完成后,需要对其进行一系列数据处理,最终得到一定范围内的速度场。进行数据处理区域,如图4所示,被分为164×78个边长为1 mm的正方形。这些正方形被称为查询区域。通过对连续两幅粒子图像进行互相关计算得到每个查询区域内的位移矢量,根据两幅图像的时间间隔求出该区域的速度矢量。对所有查询区域进行上述计算即可得到流动速度场。同时,为分析流场振荡的时频特征,在流场振荡较为明显的格栅内外两侧均匀地选取若干测点,其位置在图4中标出。在x方向,各测点距格栅边缘1/2G。在y方向,格栅内外侧测点与格栅内外边缘的距离均为G。其中,测点A将在“2.2”节和“2.3”节的讨论中使用。
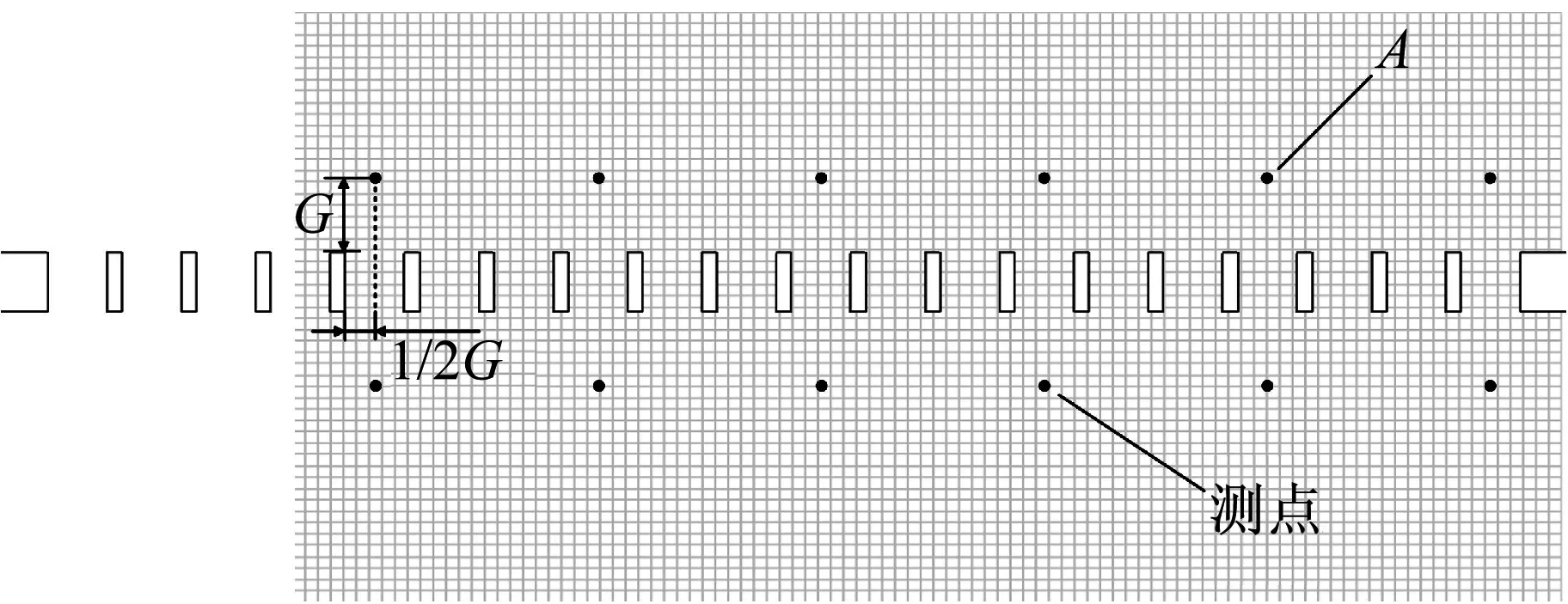
图4 查询区域及测点
TR-PIV系统所测实验数据为测量区域内不同位置的瞬态流动速度u,其在x和y方向上的速度分量分别为ux和uy。以来流速度u∞为特征速度,则流场中任意一点的无量纲流动速度分量分别为ux/u∞和uy/u∞。
在研究流场振荡的频谱特性之前,需要对流动速度时序进行快速傅里叶变换(FFT)。为避免产生频谱泄露,本文选择汉宁窗(Hanning window)函数对数据进行处理。
对速度振荡频率f进行无量纲化处理。相应的无量纲参数为斯特劳哈尔数,其表达式为Sr=fL/u∞。
1.5 实验误差分析
实验使用的示踪粒子的密度为0.91 kg/m3。在空气中的沉降速度为2.682×10-11m/s。在来流速度为10 m/s的情况下,示踪粒子与空气的相对速度几乎为0,即该示踪粒子跟随性良好。因此,由示踪粒子带来的误差几乎可以忽略。其他可能的误差来源有测量误差和互相关算法的误差,这部分误差约为1%~2%。
2 流场自激振荡时频特征
流场自激振荡伴随着复杂的流动现象,为把握其基本规律。本节对其时频特征进行分析,明确描述流场振荡过程的关键参数。
2.1 流场结构演化过程
图5利用流动速度矢量展示了流场结构的演化过程。在流体从格栅外侧流经空腔开口的过程中,格栅肋片周围会形成明显的大尺度涡团结构(图中虚线标出)。在tu∞/L=0.01时刻,大尺度涡团初步形成。从观测方向看,该涡团沿顺时针方向旋转。在外侧流动的驱动下,涡团逐渐向下游方向运动,并逐渐聚集增大。在tu∞/L=1.53时刻,涡团运动至格栅后部,受格栅末端壁面限制,涡团被压缩。在tu∞/L=1.78时刻,涡团运动至格栅末端,被壁面分割并逐渐耗散。上述过程是按照一定周期持续产生的,所产生的涡团依次向下游运动。在其影响下,流场流动参数会产生一定的波动。由此可见,大尺度涡团的运动是产生流场自激振荡的重要原因。

(a) tu∞/L=0.01
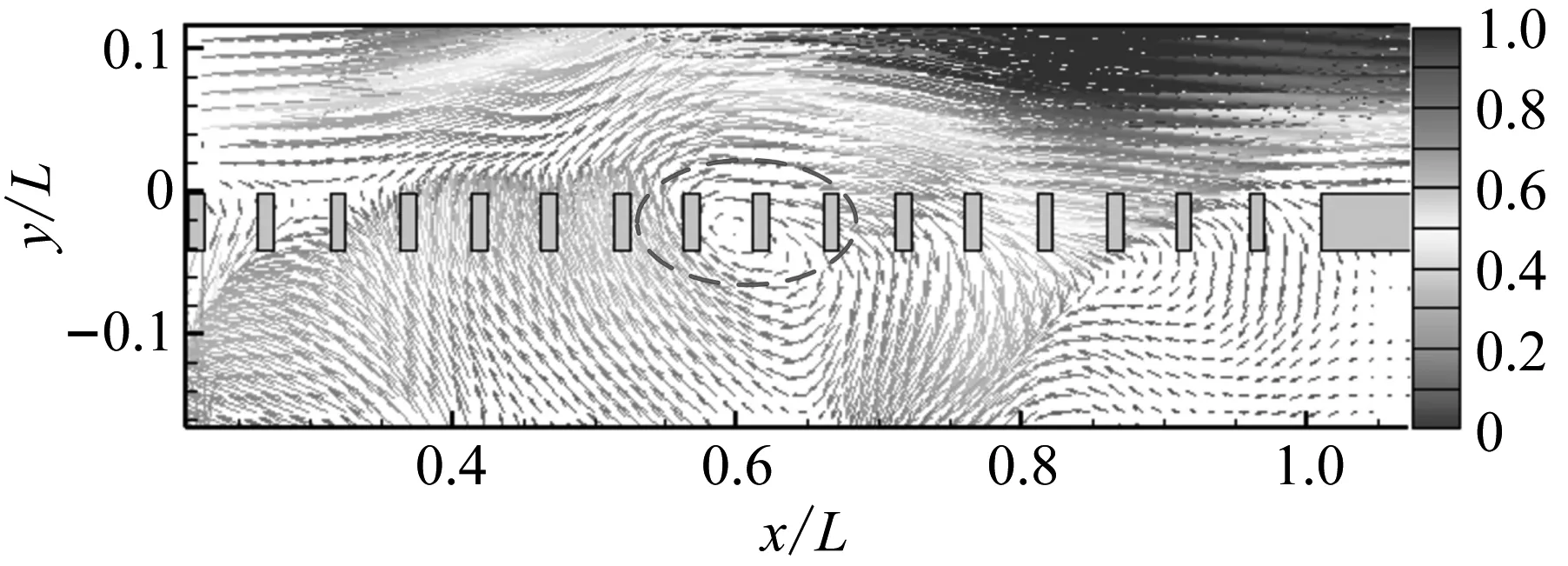
(b) tu∞/L=0.52
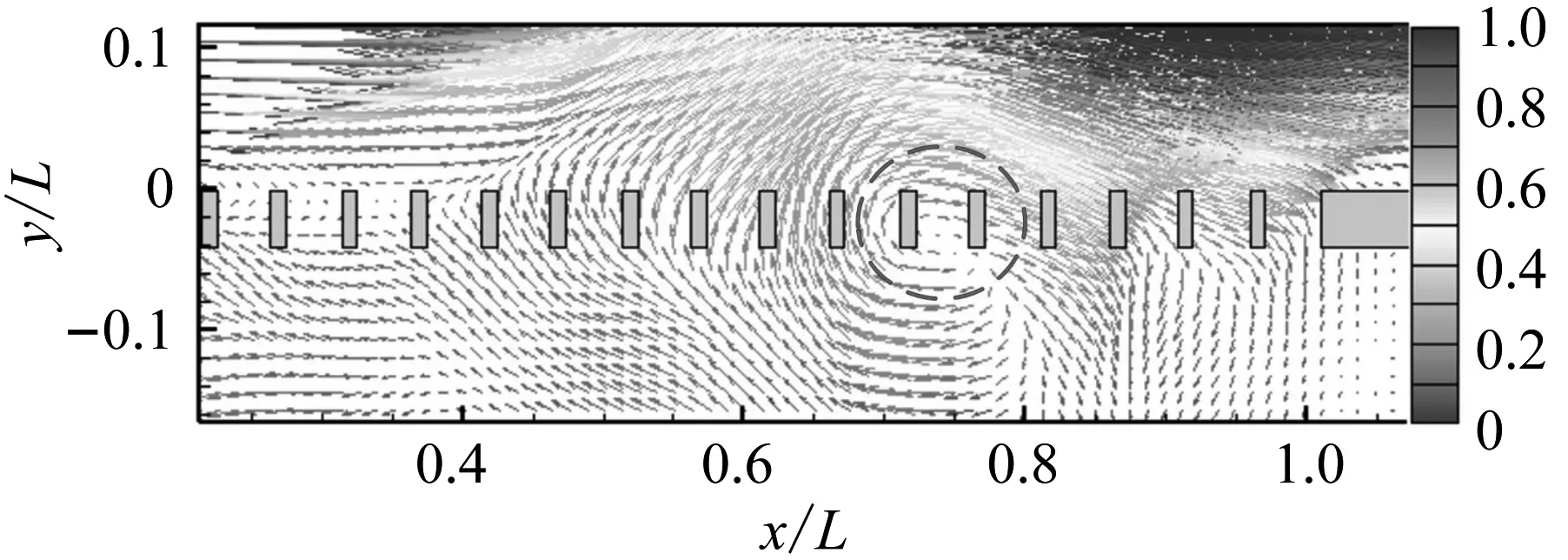
(c) tu∞/L=1.02

(d) tu∞/L=1.53
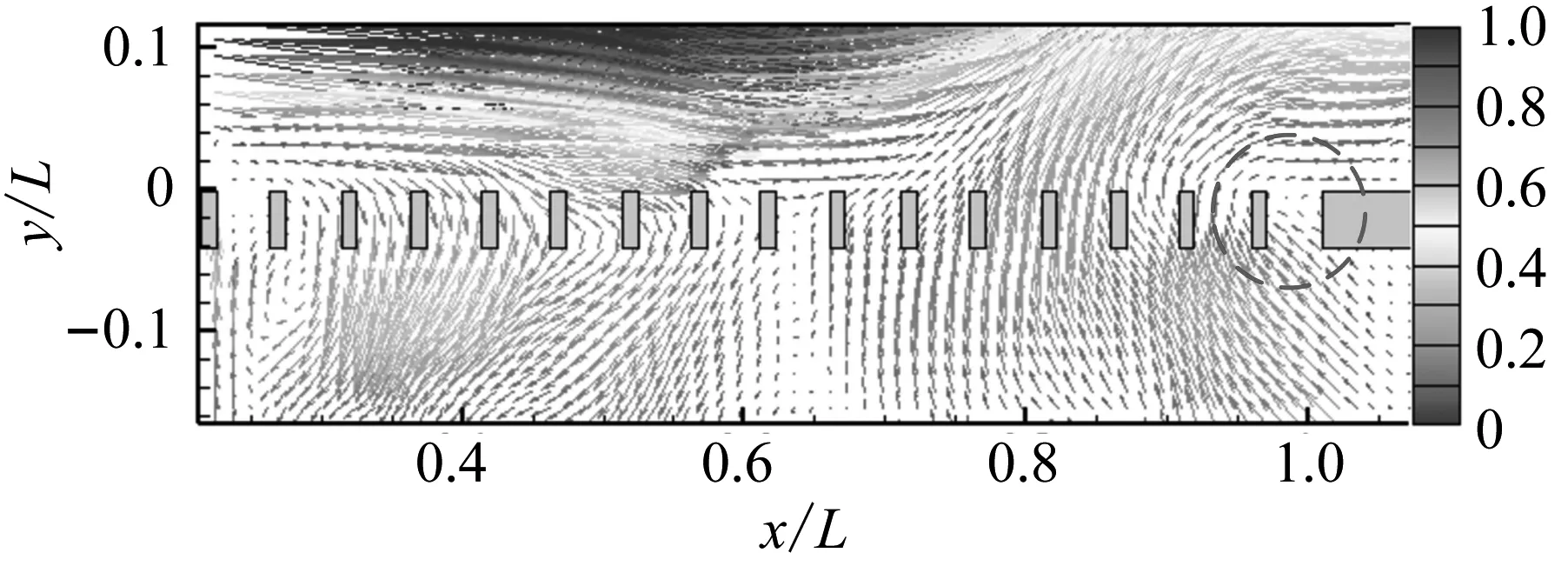
(e) tu∞/L=1.78
2.2 流场自激振荡时域特征
流场速度变化规律能够反映流场自激振荡的基本特征。图6显示了测点A所测x,y方向无量纲速度分量ux/u∞、uy/u∞的时程曲线,其中ui表示ux或uy。从图6可知,该位置不同方向的流动速度分量均处于持续振荡的状态。其中,ux/u∞和uy/u∞的算数平均值分别为0.45和0.01,两者均在其附近一定范围内振荡。同时,其振荡幅值基本稳定,振荡峰值之间的时间间隔基本相同,说明其振荡过程具有一定周期性。在没有外界激励作用的情况下,流场内产生的这种持续周期性振荡即为自激振荡。
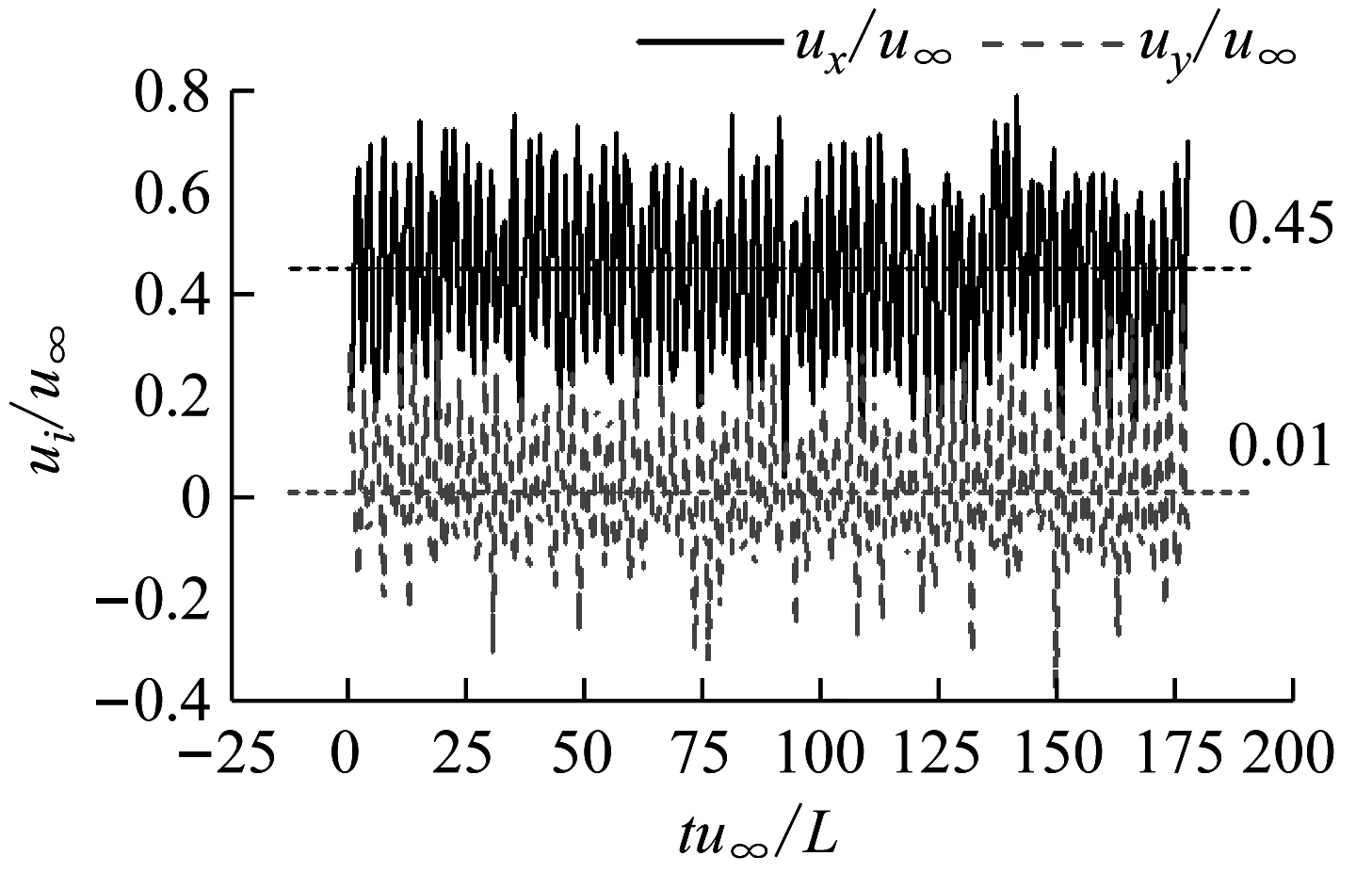
图6 速度时程曲线
2.3 流场自激振荡频域特征
为分析流场振荡的频域特征,将上述时序数据进行傅里叶变换,得到如图7所示的速度分量振荡频谱。无量纲速度分量ux/u∞和uy/u∞的振荡频谱十分相似。在所测范围内,振荡频谱具有两个谱峰。峰值频率的斯特劳哈尔数分别为St1和St2。其中,St1=0.37,St2=0.74,可得St2=2St1。显然,此类流场自激振荡是由基频成分(St1)与谐波成分(St2等)叠加而成的。从振荡幅值看,x,y方向速度分量的基频峰值分别为Pux和Puy。谐波成分所对应的峰值振幅远小于基频成分。因此,基频成分体现了流场自激振荡的主要过程,故选取基频Sr1及其对应的幅值Pux、Puy等参数描述流场振荡的频域特征。

图7 无量纲速度振荡频谱
3 流场自激振荡空间分布特征
本节讨论格栅周围流场振荡频率、幅值在不同空间位置的分布特征。如前所述,格栅-空腔流动所激发的流场自激振荡主要体现为流动在x,y方向产生的剧烈波动。因此,在讨论其空间分布特征时首先从x-y平面的振荡分布特征入手,随后扩展至z方向进行研究。
3.1 x-y平面流场振荡分布特征
图8给出了格栅周围不同位置处x方向速度分量的振荡频谱。从总体上看,流场不同位置均存在不同程度的振荡现象。在大部分位置,振荡频谱中仅存在一个较为明显的峰值,所对应的基频St1均为0.37,即流场不同位置的振荡频率相同。振荡幅值的分布具有如下规律:在x相同的情况下,格栅外侧振幅普遍大于格栅内测;在格栅外侧,随x的增加,振幅呈现增大-减小-增大的变化方式;在格栅内侧,随x的增加,振幅先增大后减小。
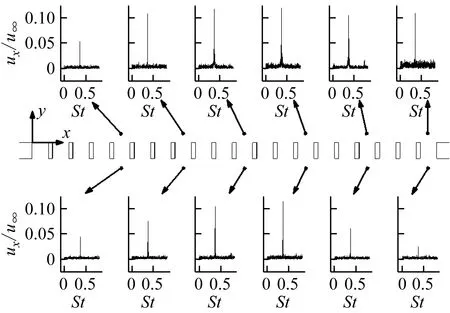
图8 格栅周围不同位置ux/u∞的振荡频谱
y方向速度分量的振荡频谱变化趋势与x方向基本相同,如图9所示。两者的不同点在于:在格栅外侧,y方向速度分量的振幅随x持续增加,未出现非单调变化现象。与之类似,图10所示的合速度的振荡频谱与x方向基本相同。
综合上述测量结果可知,在自激振荡的影响下,流场中不同方向的流动速度均会产生周期性波动。在x-y平面上,流场自激振荡的频谱分布特征见本节第一段关于x方向流动速度振荡频谱特征的阐述。振荡幅值的变化方式与“2.1”节所述大尺度涡团的运动状态密切相关。在格栅前中部,随着x的增加,大尺度涡团逐渐形成并不断增长,速度振荡幅值也随之逐渐增大。在格栅后部,大尺度涡团被压缩,速度振荡幅值出现小幅下降。在格栅末端,大尺度涡团与箱体平面发生冲击。根据大尺度涡团的旋转方向可知,冲击主要发生在格栅外侧。因此,格栅外侧速度振荡幅值较大,而受冲击影响较小的格栅内侧速度振荡幅值则很小。
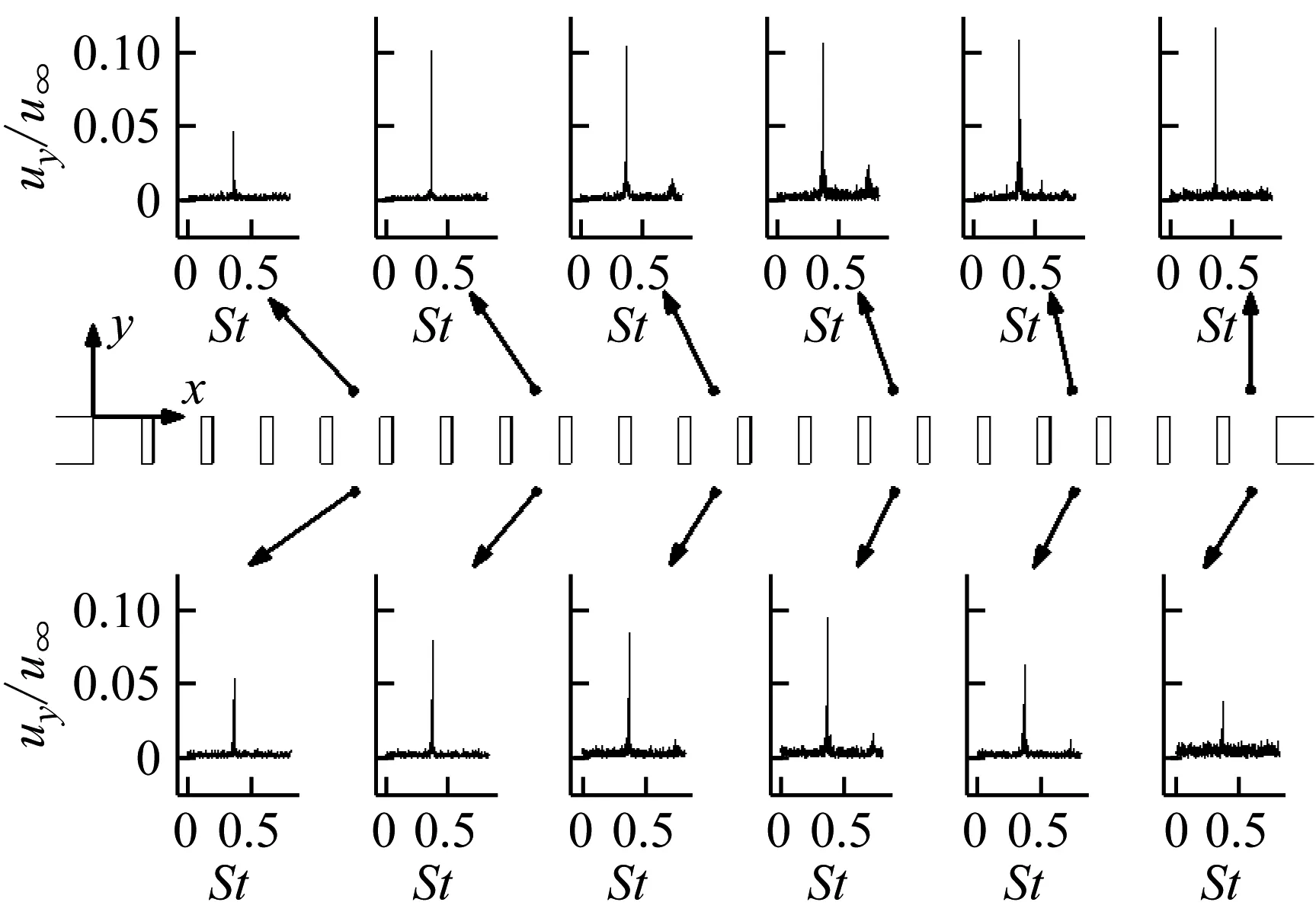
图9 格栅周围不同位置uy/u∞的振荡频谱
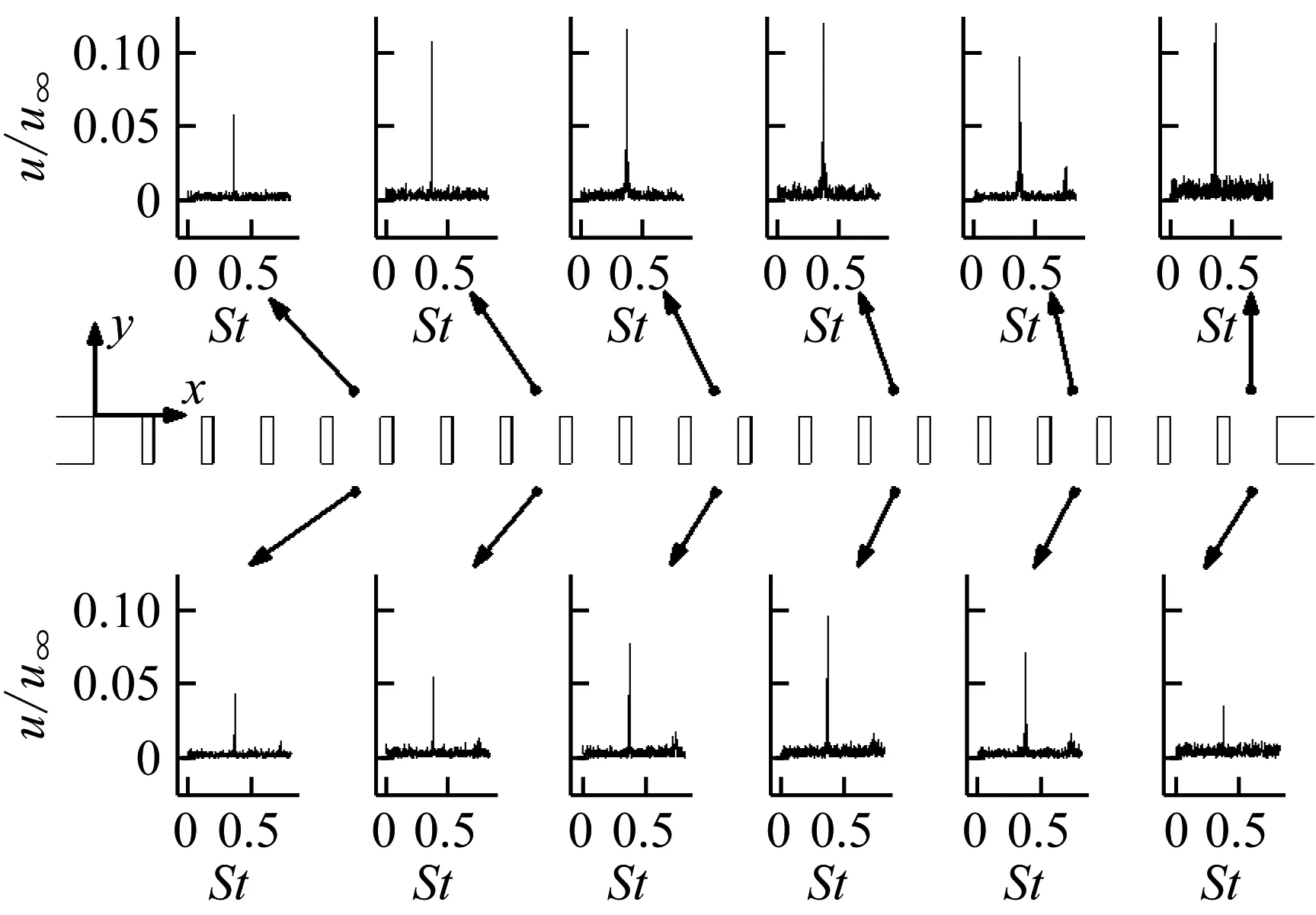
图10 格栅周围不同位置u/u∞的振荡频谱
3.2 z向流场振荡分布特征
z方向即为流场的展向,如图2、图3所示。以往研究多将格栅-空腔流动作为二维流动问题进行处理。故只关注x-y平面内的流动现象。为明确流场振荡的三维空间分布特征,本节对处于不同z位置的流场结构及流场振荡频率、幅值进行分析。
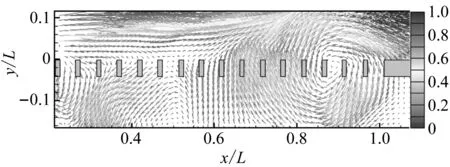
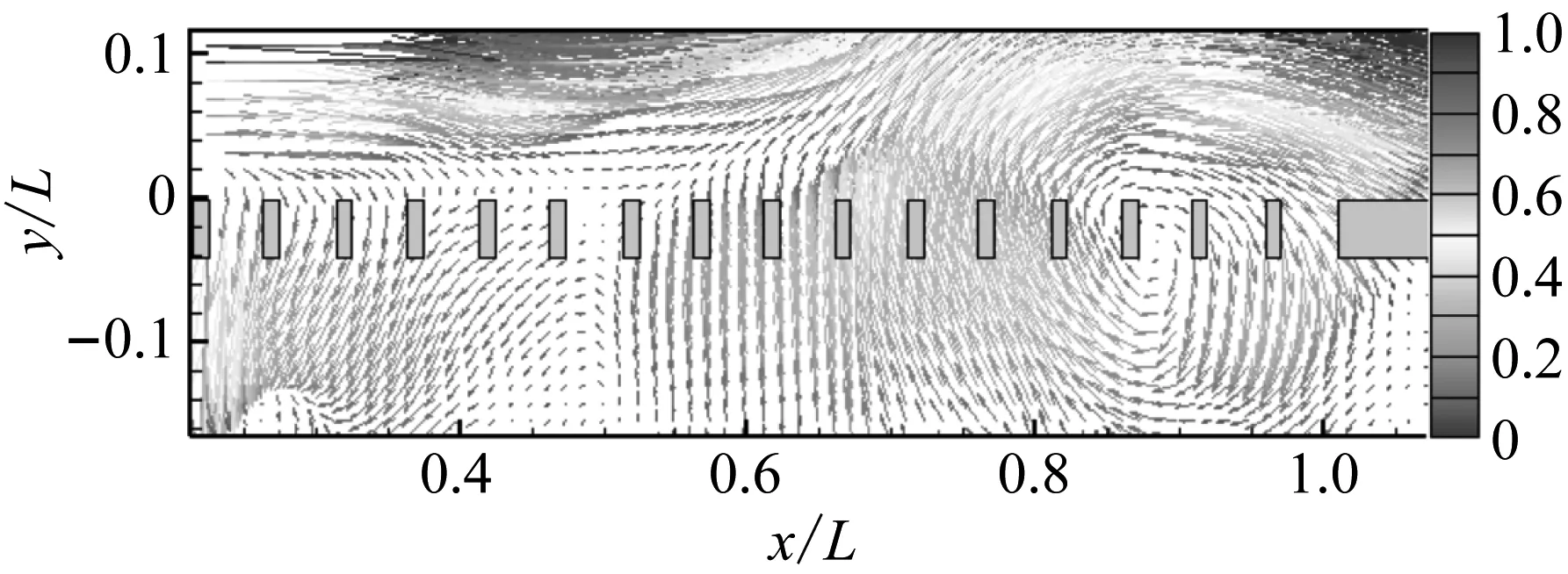
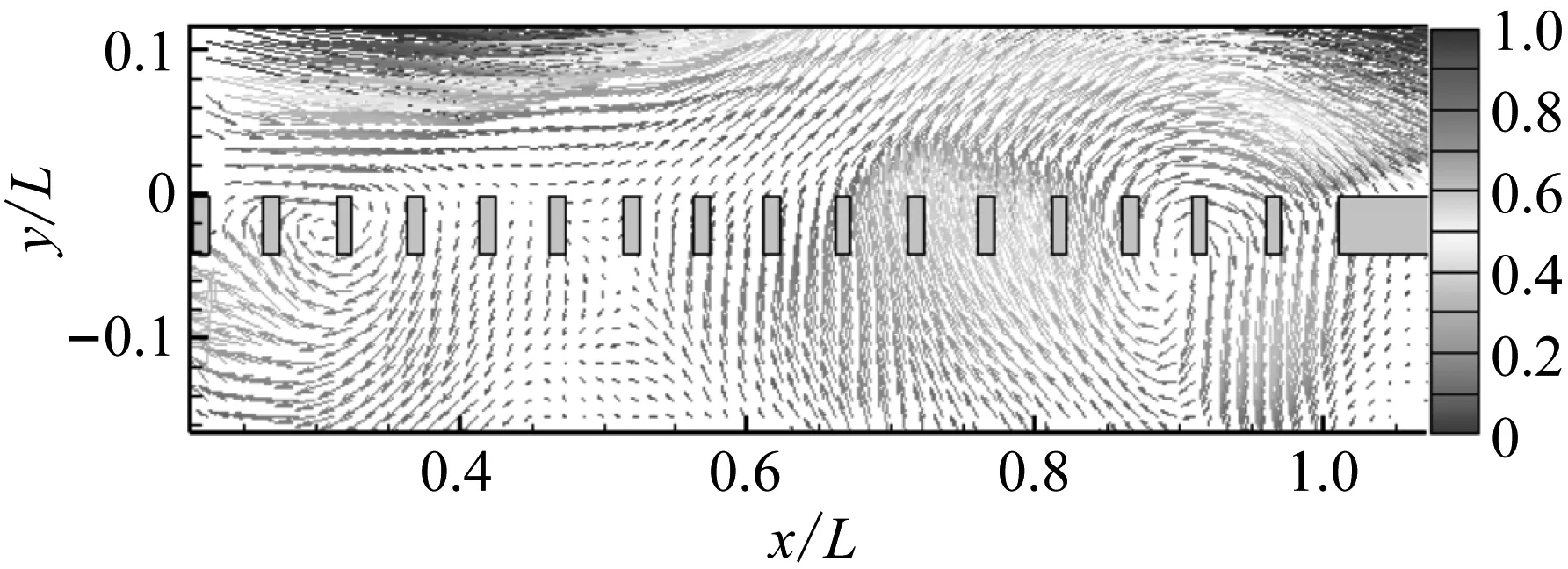
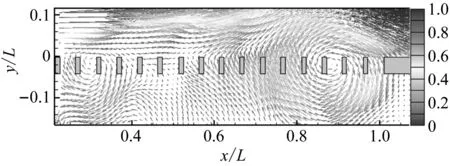
图11对比了不同z向测量截面相同振荡相位的速度矢量。在图11所示的时刻,大尺度涡团的位置、旋转速度、影响范围等基本相同。由于所选取的截面具有一定代表性,故可以推断不同z向截面的流场结构基本相同。一般情况下,二维流动假设可以成立。但是,为从定量角度进行分析,还需要对比不同z向测量截面流场振荡的频率和幅值。
图12展示了格栅外侧速度振荡频率的分布情况。不同位置的振荡频率均处于0.36~0.37。考虑到测量误差等因素的影响,可以认为流场振荡频率不随空间位置变化。该结果进一步证明了格栅-空腔流动流场自激振荡现象普遍存在于格栅附近的流场内。
(a) Wp=0.125W
(b) Wp=0.25W
(c) Wp=0.375W
(d) Wp=0.5W
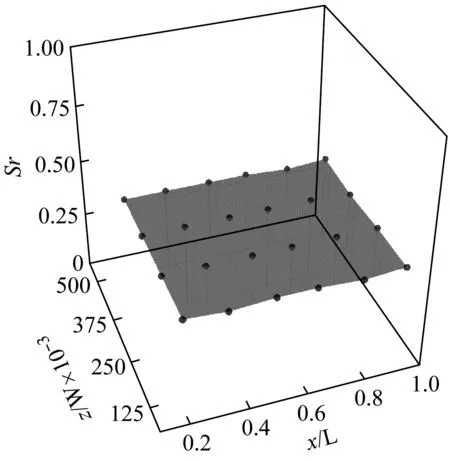
图12 格栅外侧流场振荡频率分布
由上文分析可知,在z向位置确定的情况下,格栅外侧振荡幅值沿x方向呈增加-减小-增大的变化趋势。在处于不同展向位置的x-y平面上,流场振荡幅值Pu均遵循上述变化规律,如图13所示。另一方面,在x方向位置确定的情况下,振荡幅值沿z方向逐渐增加,即远离空腔壁面的位置振荡幅值较大。
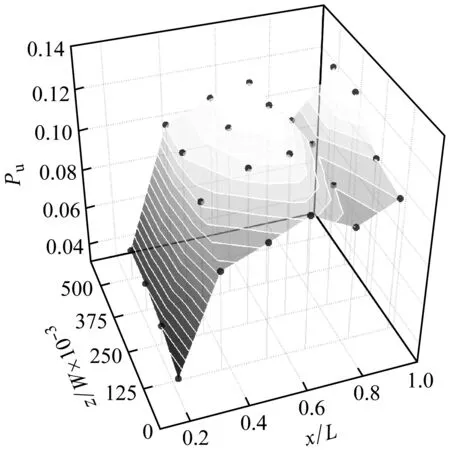
图13 格栅外侧流场振荡幅值分布
格栅内侧流场振荡频率的分布情况,如图14所示。可以看出,格栅内侧振荡频率的数值及分布情况均与格栅外侧相同。由此可知,在流场自激振荡的影响范围内振荡频率处处相同。
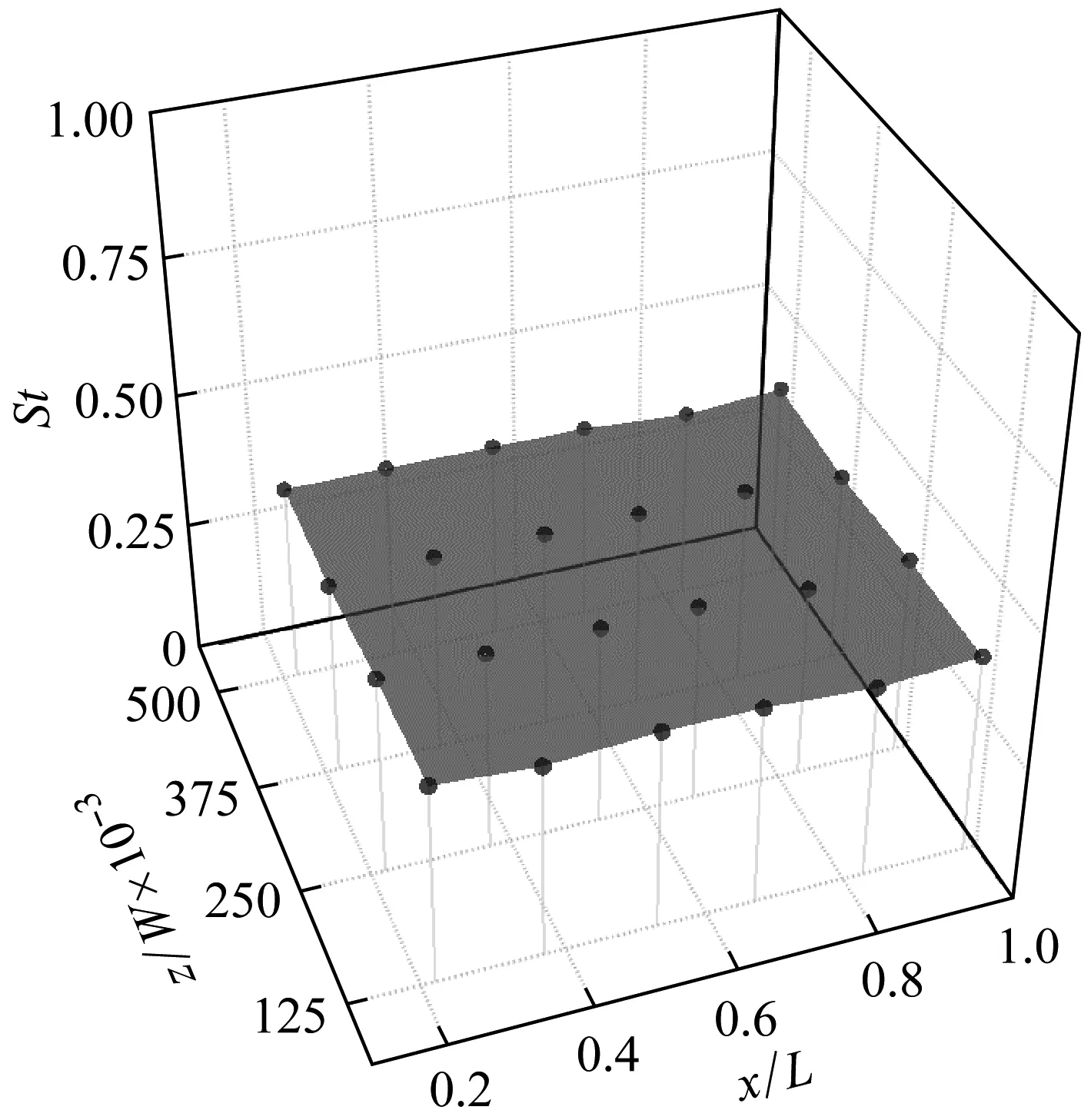
图14 格栅内侧流场振荡频率分布
图15显示了格栅内侧流场振荡幅值的分布情况。与格栅外侧类似,不同展向平面中振荡幅值的变化规律一致,均为随x的增加先增大后减小。同时,振荡幅值沿z方向逐渐增加。如前所述,该流动具有对称性,其对称面为z=0.5W的中心平面。因此,当z>0.5W时,振荡幅值沿z方向逐渐减小。即振荡幅值随测量位置与空腔侧壁之间距离的增加而增加。
根据不同z向截面的流场结构和振荡频率的分布可以看出,流场振荡的基本特征沿z方向基本一致。无论是格栅外侧还是内侧,远离空腔侧壁处的振荡幅值均大于贴近侧壁处。这种分布方式可能是由于壁面对流动的阻力所造成的。在贴近壁面的位置,由于壁面与流体之间的黏性作用,一部分振荡能量被消耗,从而造成该位置振荡幅值较低。
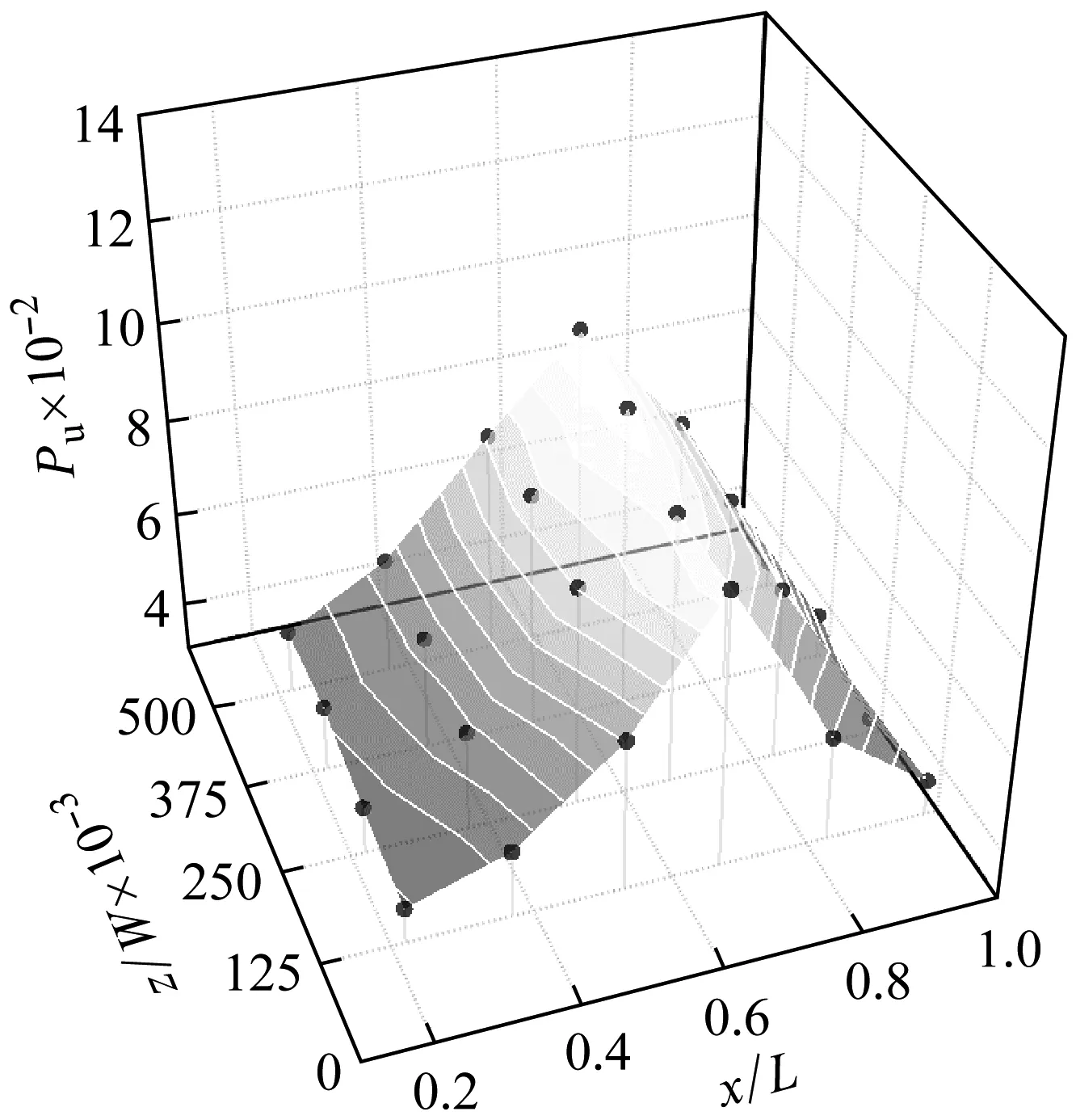
图15 格栅内侧流场振荡幅值分布
综合格栅内外两侧的测量结果可将格栅-空腔流动流场自激振荡的空间分布特征总结如下:流场不同位置的振荡频率相同。在格栅外侧,振荡幅值沿x方向呈先增大后减小最后再次增大的变化趋势。在格栅内侧,振荡幅值沿x方向呈先增大后减小的变化趋势。在z方向,振荡幅值的分布以z=0.5W的中心平面为对称面,在对称面处达到最大值,沿该平面法向方向逐渐减小。
4 结 论
通过风洞实验对格栅-空腔流动流场自激振荡现象进行了研究,使用TR-PIV系统测量了流场不同位置的流动速度场,分析了流场自激振荡的空间分布规律。得到的主要结论有:
(1) 格栅-空腔流场中不同位置的自激振荡频率相同。
(2) 在格栅外侧,流场振荡幅值沿来流方向经历增加-减小-增加的变化过程。在格栅内侧,流场振荡幅值沿来流方向经历先增加后减小的变化过程。
(3) 在展向方向,振荡幅值在中间对称平面达到最大,并向空腔两侧逐渐减小。
