风力机地震诱导机舱振动非线性特性分析

刘中胜， 杨 阳， 李 春,2， 邹锦华， 袁全勇

(1. 上海理工大学 能源与动力工程学院， 上海 200093； 2. 上海市动力工程多相流动与传热重点实验室， 上海 200093)

为减少温室气体排放、缓解日益突出的环境问题，风能因其资源广泛和利用技术成熟等特点，已然成为世界各国主要发展的清洁能源之一。据全球风能协会统计，2016年，全球新增装机容量达54.6 GW，其中我国占比42.8%，位居世界首位[1]。我国新建风电场主要位于西北、华北和东南沿海等地区。其中西北地区和东南沿海分别处亚欧大陆地震带和环太平洋地震带。在时域非定常和空间非均匀的湍流风作用下，风力机结构气弹响应具有十分明显的非线性和非平稳特征[2-3]。若此时发生地震，风力机系统受到高强度地震载荷的持续激励，塔基载荷将明显增大[4]。不仅会增强结构振动，还可能导致塔架发生屈曲和塑性变形等结构损伤。由于风力机属于堆积质量的弹性体力学结构，塔架底部塑性发展将影响顶部结构安全，地震诱导塔顶剧烈振动进一步增大了整机倒塌的危险。因此，研究结构地震动力学响应特性，对于风力机结构设计和安全校核具有十分重要的意义。

国内外相关学者一般采用频域法或有限元法分析风电结构地震动力学响应，但均对风力机进行了一定的简化：将风轮和机舱简化为塔顶堆积非旋转集中质量。其中，频域法基于塔架固有频率、模态振型及质量分布，再根据所选的地震反应谱计算地震载荷[5-8]。由于该方法忽略了气动阻尼和高阶模态影响，导致计算结果保守，且无法获得结构动力学响应的时域演化特性。

美国凯斯西储大学基于小型风力机开展的相关实验研究发现[9]，地震发生时塔顶侧向位移会突然急剧增大。说明结构异常振动特性亟待进一步研究及开展时域分析研究结构瞬时地震响应的必要性。有限元法可以分析风电结构地震动力时域响应，但气动载荷被简化为轴向推力甚至被忽略[10-14]。Zhao等[15-16]采用了多体动力学方法建立了计算效率更高的结构动力学模型，研究了风力机地震动力响应特性，但采用轴向推力代替非定常风轮气动力的方法过于简单。

随着风力机大型化发展，气动载荷显著增大，气动阻尼对结构动力学响应的影响不可忽视[17]。加州大学圣迭戈分校开展的65 kW风力机地震振动试验研究结果表明，叶片气动弹性效应使得部分能量被湍动气流耗散，在地震结束后，正常运行工况的结构振动幅度降低速度比停机工况更快[18]。因此，对于大型风力机，更需要考虑非定常气动力与瞬时地震激励在来流方向的耦合效应。

地震发生时，进行相应的控制是减弱地震损伤的有效措施。借鉴土木工程抗震防灾控制方法，目前风力机抗震控制研究主要集中于调谐减振阻尼器的被动控制方式[19-20]。由于地震载荷属于高强度的短时激励，被动控制无法保证结构安全。而进行主动控制，首先需要全面分析结构地震诱导振动的非线性特征，同时还需要对响应规律进行预测，以进行有效的主动控制。而简单的FFT方法的频率响应是基于全局时域特征，不能区分引起非平稳响应的真正频率。尽管小波变换可同时从时域和频域对响应信号进行多尺度联合分析，其局部细化分析能力可有效区分突变信号频率和非平稳白噪声频率，但结果准确性严重依赖于小波基函数的选择，如何针对特定问题准确的选择基函数十分困难。

针对以上问题，首先通过Wolf方法[21]建立土-构耦合模型，结合地震运动规律计算地震载荷，并基于风力机气动弹性仿真开源软件FAST[22]建立考虑风-震耦合的风力机地震动力学仿真模型。其次，通过分形理论和混沌识别方法分析结构动力响应的非线性特征，计算塔顶振动加速度时间序列的分形和混沌非线性特征参数，为风力机结构地震动力响应研究和抗震控制及短期预测提供参考。

1 地震动力学仿真模型

基于气动弹性仿真软件FAST计算气动载荷，采用Wolf模型表示土-构耦合效应，通过自编译程序实现地震载荷计算功能。在FAST中耦合气动力及地震激励，获取风力机结构动力学响应。

当地震发生时，风力机系统目标加速度为地震加速度，此时基础平台γ方向地震载荷Fγ为

Fγ=-Kγ(dγ-dγ,t)-Cγ(Vγ-Vγ,t)

(1)

式中：γ为方向；dγ和Vγ分别为风力机基础平台γ方向的实际位移和实际运动速度；dγ,t和Vγ,t分别为基础平台γ方向的目标位移和目标速度。

基于Wolf方法建立土体与风力机基础平台的耦合模型：将土体与结构之间的相互作用等效为弹簧振动，通过定义弹簧振子的刚度与阻尼，即可将地震运动转化为地震激励。土体与结构之间的耦合作用(Soil-Structure Interaction，SSI)，如图1所示。

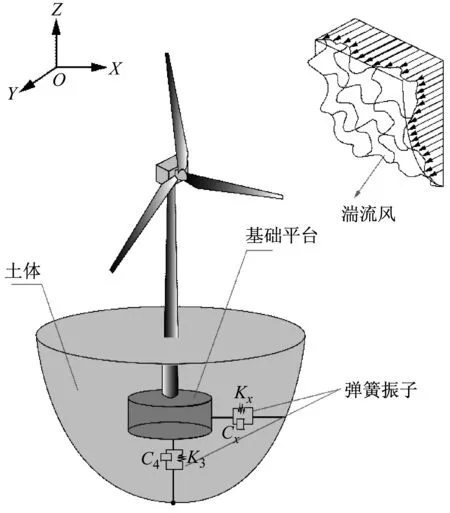
图1 土体与风力机基础平台耦合模型

各方向K和C通过式(2)和式(3)计算

(2)

(3)

式中：下标x和y为水平方向，其中x为入流方向，下标z表示垂直方向；Gs、μs和ρs分别为土地的切变模量、泊松比和密度；Rs为基础平台的半径。

加入地震计算功能的风力机结构动力学仿真流程，如图2所示。

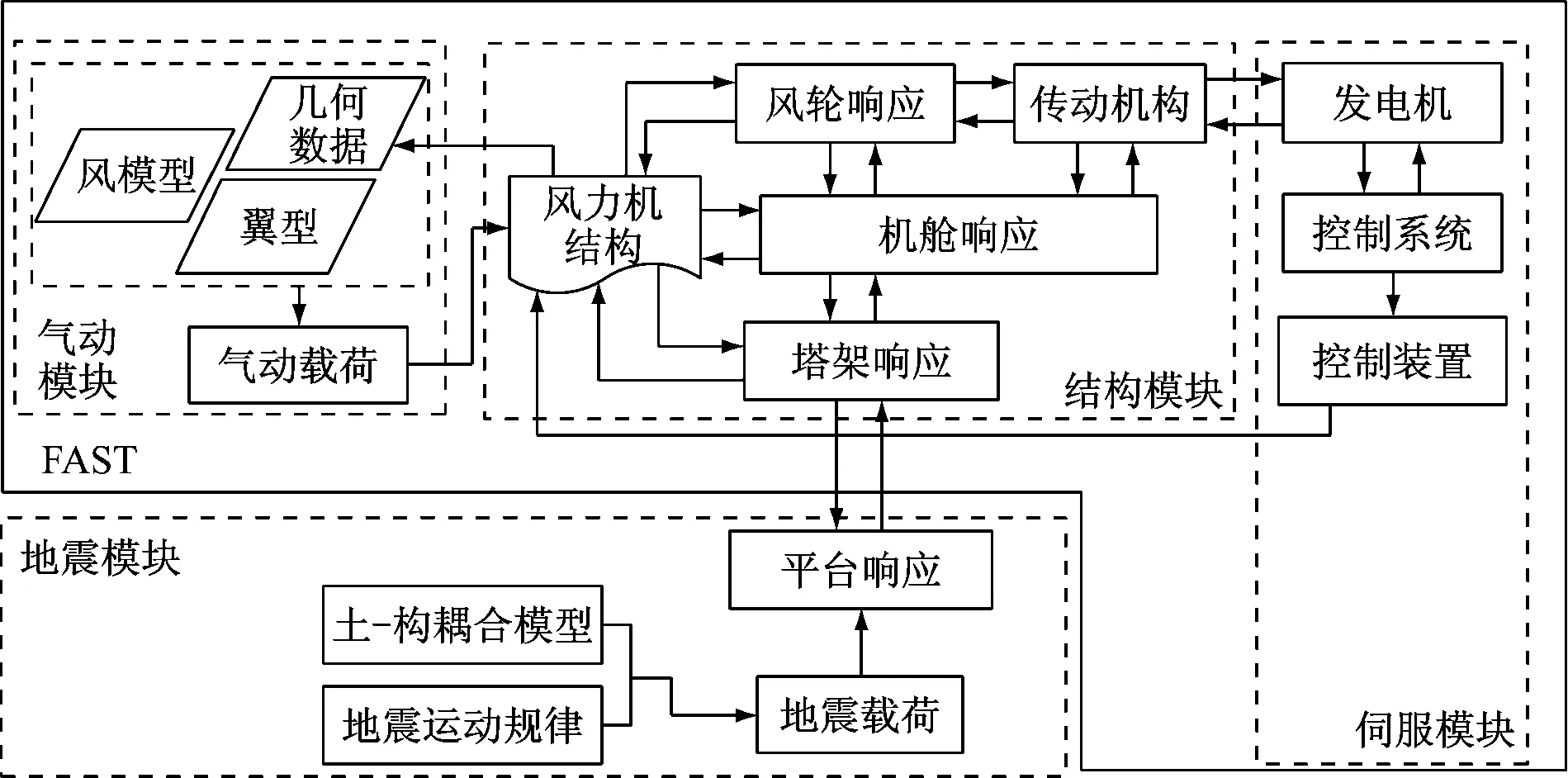
图2 地震动力学仿真流程图

2 研究对象及载荷环境

2.1 风力机结构

研究对象为50 kW的小型风力机AOC 15/50、1.5 MW的中型风力机WindPACT 70/1500以及5 MW 的大型风力机NREL 126/5000。风力机主要性能参数如表1所示[23]。

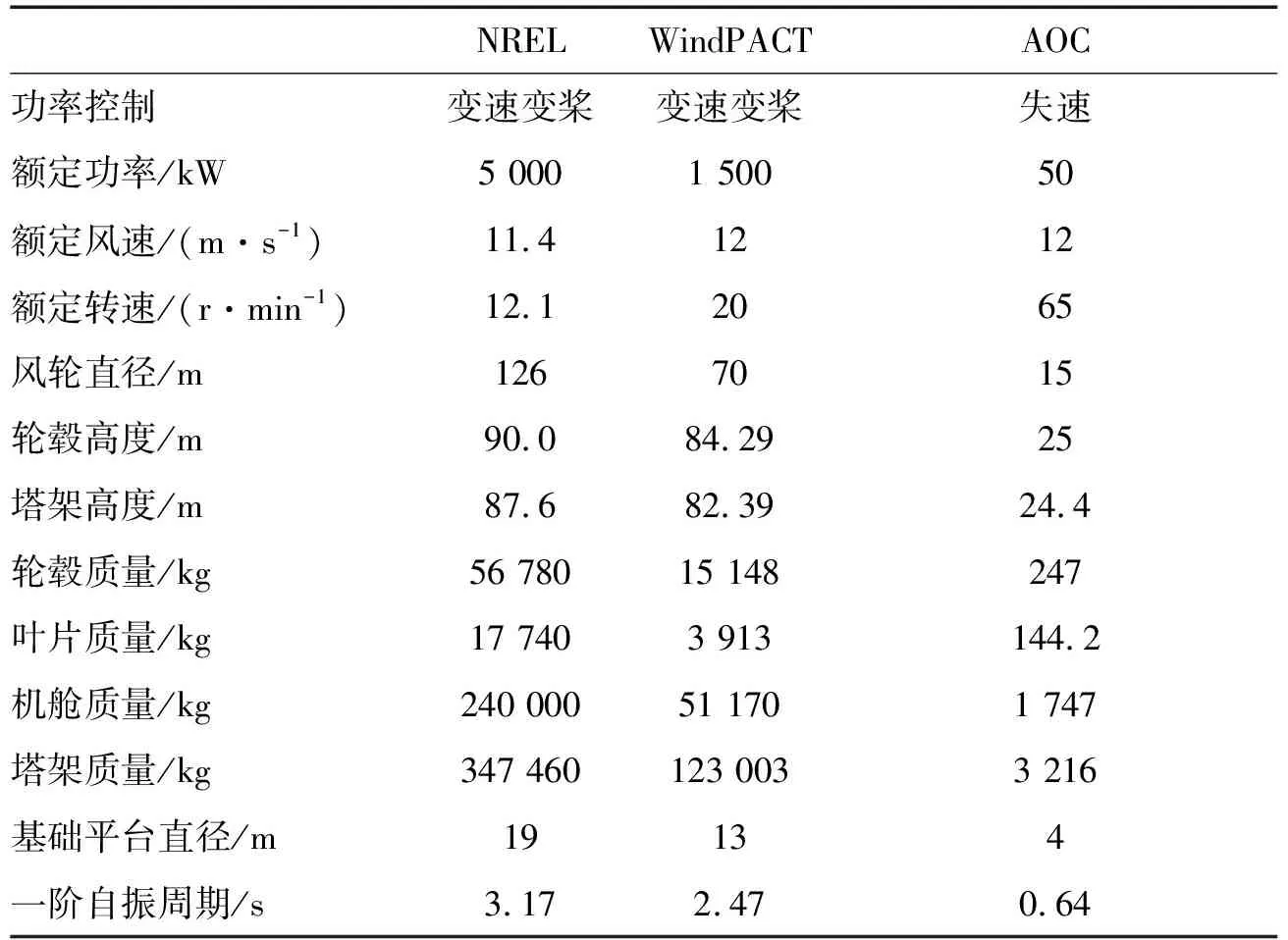
表1 风力机主要结构及性能参数

2.2 载荷环境

2.2.1 风场环境

假设三台风力机运行于同一地理位置，10 m高度处的平均风速为7.5 m/s，考虑风剪切现象，垂直高度的风速大小满足指数为0.2的指数分布，则AOC、WindPACT及NREL 风力机轮毂高度处平均风速分别为9.01 m/s、11.49 m/s和11.64 m/s。基于Kaimal湍流风谱，通过TurbSim[24]模拟适用于各风力机的湍流风场，轮毂高度处风速时程变化曲线，如图3所示。

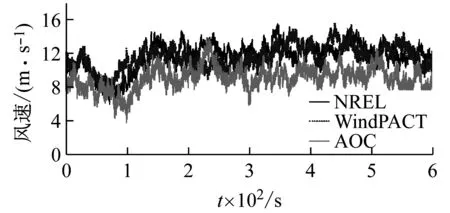
图3 风力机轮毂高度处风速时域变化

2.2.2 地震运动

选择5种发生于不同地区的地震，表2为各地震发生地点、时间和震级等信息[25]。图4为各地震运动在不同自振周期时的伪谱加速度变化特性，图中TA1、TW1和TN1分别为AOC、WindPACT和NREL风力机一阶自振周期。

表2 地震记录

图4 地震伪谱加速度

3 分形及混沌非线性分析方法

分形和混沌是20世纪提出用于研究非线性问题的两门学科。其中，分形由Mandelbrot于1967年首次提出，通过分形维数定量描述具有自相似性的几何形态。1963年，Lorenz混沌理论用于研究动力学系统中不可预测和类似随机的运动。

3.1 分形维数

分形维数是分形理论的核心概念，用于定量描述非线性信号的自相似特性和分形特征，可通过计盒维数法进行计算。图5为任意曲线信号的盒子覆盖示意图[26]。

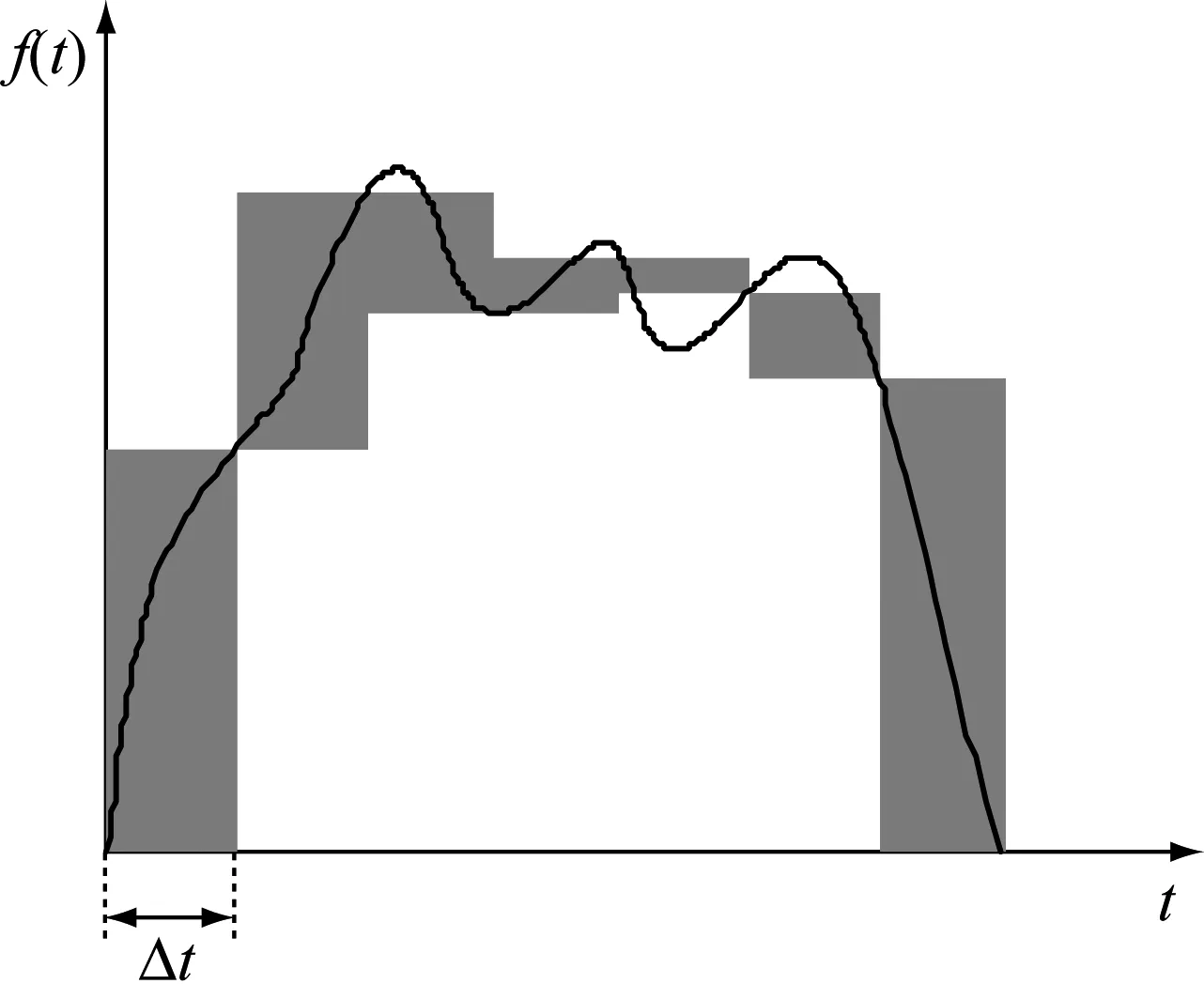
图5 计盒维数法盒子覆盖任意信号曲线示意图

对于任意信号曲线，分形维数可表示为

(4)

式中：D为分形维数；Δt为时间步长。NΔt为盒子宽度为Δt时覆盖信号曲线的面积，如式(5)

(5)

式中：p为信号数据容量；f(ti)为ti时刻对应的信号值。

对于有限数据容量的信号，可通过最小二乘法线性拟合不同尺度Δt及对应的NΔt得到，分形维数D为斜率，则式(4)可表示为

lg[(NΔt)/Δt2]=D·lg(1/Δt)+b

(6)

式中：b为该拟合直线的截距。

3.2 相空间重构及大Lyapunov指数

混沌理论用于研究非线性动系统不规则的复杂响应，具有混沌特征的非线性系统可进行短期行为预测。混沌吸引子是混沌系统的基本特征之一，根据Takens定理，通过求取合适的延迟时间和嵌入维数，即可通过相空间重构得到混沌系统的吸引子。相空间重构详细算法可见文献[27]。针对任意非线性响应信号，可通过最大Lyapunov指数λ判断系统响应是否具有混沌特征。当λ>0时，系统动力学响应具有混沌特征，且其值越大，非线性越强，可预测时间与λ成反比。λ可表示为[28]

(7)

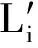
4 有效性验证

为验证本文地震动力学仿真模型的有效性，与Asareh和Prowell基于FAST建立的地震动力学仿真程序Seismic进行对比[29]。以NREL 5 MW风力机为计算对象，选择1969 EI Centro地震加速度谱，仿真时间为600 s，时间步长为0.002 s，在400 s时加入地震。图6和图7分别为塔顶位移时域响应和塔架不同高度处位移最大值对比。从图7可知，本文计算结果与Asareh和Prowell等计算结果吻合度极高，时域响应基本重合，仅塔顶位移最大值略有不同，误差为1.5 %。与Asareh和Prowell等计算结果对比可以发现，采用本文建立的地震动力学仿真模型的计算结果具有较高的可靠性和准确性。

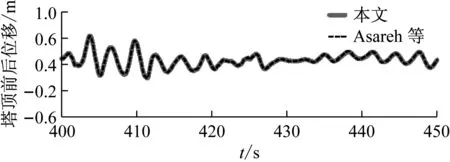
图6 塔顶位移时域计算结果对比

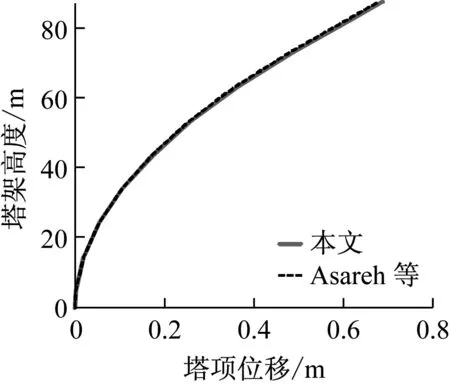
图7 塔架不同高度处位移最大值

5 结果分析

风力机在正常工况下运行，算例仿真时间为600 s，时间步长0.002 s，在400 s时加入地震载荷，地震持续时间为50 s。

5.1 机舱加速度时域响应

图8为Chi-Chi地震作用下的三台风力机机舱振动加速度时域变化。

(a) Chi-Chi地震

(b) NREL

(c) WindPACT

(d) AOC

从图8可知，AOC风力机机舱振动加速度响应规律基本与地震加速度相同，WindPACT风力机在地震加速度较小的时间段内(400～ 420 s)，其机舱响应规律与地震加速度相同，NREL风力机则没有这一现象，说明风载荷对机舱振动具有一定影响。随着地震加速度增大，机舱振动加速度随之增大，且x方向(来流方向)加速度更大。时域结果表明，大型兆瓦级风力机需要考虑风-震耦合效应，小型风力机则无需考虑风-震耦合效应，风力机机舱振动主要受到地震诱导作用。

5.2 分形特性

基于计盒维数法，计算了5种地震作用下三台风力机机舱振动特性的分形维数，如图9所示。

图9 不同地震时机舱加速度时间序列曲线分形维数

分形维数大小可定量表征自相似性和长程相关性，其值越大，则自相似性和长程相关性越高。由图9可知，三台风力机在不同地震作用下的机舱加速度时间序列曲线分形维数均>1.5，在1.6～1.8的区间内变化，说明风力机地震诱导振动特性在时域内具有较高的自相似性和长程相关性。在不同地震作用下，NREL风力机的分形维数大小较为平均，WindPACT风力机和AOC风力机均有一定程度的不同，说明地震对NREL风力机机舱振动影响最小。

图10为分形维数与地震震级之间的关系。从图10可知，随着地震震级增大，AOC风力机机舱振动分形维数不断增大，而WindPACT风力机和NREL风力机则没有明显规律。由于AOC风力机功率最小，相比于地震载荷，气动载荷对机舱振动的影响完全可以忽略。因此，地震强度越大，导致机舱振动波动性更大，从而具有更大的分形维数和自相关性。WindPACT风力机和NREL风力机均为兆瓦级大型风力机，气动载荷对机舱振动具有一定影响，尤其是NREL风力机，其机舱振动分形维数随着地震震级的变化最小。

以上结果表明，分形维数不仅可以作为非线性振动分析的定量参数，还可作为风-震耦合效应大小的定性描述参数。风-震耦合效应越小，分形维数与地震强度关联程度越大，反之则关联程度越小。

图10 分形维数大小随地震震级变化情况

5.3 混沌特性

通过G-P算法得到机舱振动加速度时程曲线最合适的延迟时间T，即可对其相应进行相空间重构，刻画混沌吸引子。图11为三台风力机在Chi-Chi地震作用下的机舱振动加速度相空间。从图11可知，NREL风力机机舱振动加速度信号的吸引子轨迹反复缠绕，形成一种较为细长的“絮”结构，说明此时振动加速度处于低维混沌状态。而WindPACT风力机和AOC风力机则较为发散，形成类似于“喇叭”的缠绕轨迹，分为稠密的小环线区域和较为稀疏的外围换环线区。结果说明地震作用下，风力机机舱振动表现为明显的混沌特性，即非完全随机行为。此外，三台风力机均未出现周期性的轨迹缠绕现象，说明由地震诱发的风力机机舱振动为非周期性的非平稳振动。

(a) NREL 风力机

(b) WindPACT 风力机

(c) AOC风力机

图12为三台风力机机舱振动加速度时程曲线最大Lyapunov指数分布。从图12中知，不同地震作用下，每一台风力机机舱振动信号的最大Lyapunov指数均大于0，最大值均>0.1，进一步验证了地震诱导风力机机舱振动具有明显的混沌特征。WindPACT风力机平均最大Lyapunov指数最小，NREL风力机最大。由于可预测时间与最大Lyapunov指数成反比，因此，NREL风力机地震诱导振动可预测时间最短，即说明其地震诱导振动处于最不稳定性状态。与分形维数相同的地方在于，除了AOC风力机之外，WindPACT风力机及NREL风力机地震诱导振动最大Lyapunov指数与地震震级之间均有较为明显的相关性。其中，对于WindPACT风力机，最大Lyapunov指数随着地震震级的增大而增大，说明地震强度对其振动的混沌特征具有正相关作用。而对于NREL风力机，地震强度与最大Lyapunov指数之间为负相关。

图12 最大Lyapunov指数随地震震级变化情况

6 结 论

通过数值计算AOC 50 kW、WindPACT 1.5 MW和NREL 5 MW三台不同功率大小的风力机在五种不同地震作用下的机舱振动特性，与文献结果进行对比验证了计算方法的有效性，并通过分形和混沌理论分析了风力机地震诱导振动的非线性特征，主要得到以下结论：

(1) 风力机机舱地震诱导振动具有明显的不平稳特征，小型风力机机舱振动主要受到地震载荷作用，无需考虑风-震耦合效应。气动载荷对兆瓦级风力机机舱振动具有一定影响，地震动力学仿真必须考虑风-震耦合效应。

(2) 风力机机舱地震诱导振动具有明显的分形特征，分形维数介于1.6～1.8，说明地震诱导振动在时域内具有较高的自相似性和长程相关性。

(3) 对于AOC风力机，地震诱导振动分形维数随地震震级呈现较为明显的线性增长趋势，而NREL风力机地震诱导振动分形维数对地震强度敏感程度较低。分形维数不仅可以作为非线性振动分析的定量参数，还可作为风-震耦合效应大小的定性描述参数。风-震耦合效应越小，分形维数与地震强度关联程度越大，反之则关联程度越小。

(4) 风力机机舱地震诱导振动表现为明显的混沌特性，三台风力机均未出现周期性的轨迹缠绕现象，地震诱导振动为非周期性和非完全随机的非平稳振动。

(5) 对于风-震耦合效应较强的风力机，地震诱导振动时程曲线最大Lyapunov指数与地震震级之间均有较为明显的相关性。五种地震运动下，NREL风力机平均最大Lyapunov指数最小，说明地震诱导振动的可预测时间最短，处于不稳定性状态。