基于速差反馈的独立车轮曲线通过性能分析

李浩天， 池茂儒， 梁树林， 吴兴文

(西南交通大学 牵引动力国家重点实验室， 成都 610031)

独立车轮导向难题由来已久，其自导向性能与稳定性是一对天生的矛盾。国内外学者做过大量研究，一方面，为了获得近似于传统刚性轮对的自导向能力，独立车轮耦合轮对的概念被提了出来，Dukkipati等[1-2]详细介绍了耦合轮对的发展概况和关键技术；池茂儒等[3]对磁流变耦合轮对车辆的直线平稳性、曲线通过性能进行了系统的分析，得出了耦合阻尼对车轮动力学性能的影响规律，并优化了前后轮对耦合阻尼；Mei等[4]提出了一种集成牵引、制动、导向控制于一体的轮毂电机电气耦合方式；孙效杰[5]设计了一种电气耦合轮对方案，发现采用电轴系统的耦合轮对可以达到近似于弹性阻尼耦合轮对的自导向性能；杨勇等[6]基于速差反馈提出了一种多电机同步控制策略。另一方面，为了尽量保证独立车轮的稳定性，Doyle等[7]发现了扭转耦合轮对会降低车辆临界速度；Wickens[8]提出了一种基于轮对横移量反馈的主动控制方法，并分析了车辆动态稳定性；Powell[9]以轮对摇头角速度反馈为控制量，轮对横移量为判定量，设计了一套差速器动力控制系统；Barbera等[10]提出了一种可以根据不同半径曲线实轮对耦合或分开的离合器；Wu等[11]发明了一种限滑差速器耦合轮对，并分析了不同半径曲线上，差速器耦合轮对的耦合刚度、阻尼的匹配关系以及对稳定性的影响；董小闵等[12]在简单滑模控制基础上提出了基于自适应模糊逻辑的控制策略，有效提高了车辆平顺性；任利惠等[13]基于左右车轮转速差对轮对姿态进行主动控制，发现速差控制轮对与弹性阻尼耦合轮对存在内在联系；Mei等[14]提出了一种可自适应车辆速度的简单主动控制悬挂，可以提高独立车轮的曲线通过性能和乘坐舒适度。张济民等[15]对机械式差速器耦合轮对在超小半径曲线上的通过性能进行了仿真、试验，发现差速器耦合轮对的磨耗和曲线稳定性优于刚性轮对。上述研究表明，车轮耦合可以使独立车轮在直线和大半径曲线上的自导向能力接近传统刚性轮对，但同时也会降低车辆临界速度。

车轮主动控制是独立车轮车辆的关键技术，主要有基于转速反馈和转矩反馈两大类，转矩控制要求知道曲线半径和蠕滑率，转速控制要求知道曲线半径和车轮转速，转速导向效果优于转矩导向[16]。直线和大半径曲线上，独立车轮的导向问题容易解决，只要将两侧车轮转速有效耦合起来即可获得近似于传统刚性轮对的自导向性能；小半径曲线上，机械差速器加装离合装置可以使耦合轮对还原成独立车轮，进一步减小车轮冲角和磨耗，但是仅通过机械方式，无法保证车轮在小半径曲线上的转速合理，内外车轮转速还会受轮轨粘着条件、轮缘贴靠等因素的影响。能否规避机械差速器的弊端？怎样实现独立车轮合理差速？如何兼顾车辆的自导向和通过性能？

针对上述问题，本文从汽车差速原理出发，分析了不同曲线半径上独立车轮铁道车辆运用机械差速器的可能性和等转矩控制的适应性，并提出了一种新方案——基于转速反馈的电差速主动控制。

1 机械差速原理

1.1 汽车差速原理

汽车通过曲线时内外车轮的差速是通过差速器实现，应用较广泛的是对称式锥齿轮差速器[17]，其构造如图1。差速器力矩分配特性决定了阻力大的一侧转速慢，阻力小的一侧转速快。

图1 对称式锥齿轮差速器

汽车轮胎相当于无数个弹簧阻尼并联，目前较多采用Bouc-Wen模型[18]来描述，如图2，其与地面接触点前点被压缩，处于加载状态，后点恢复，处于卸载状态，前点的地面法向反力大于后点，阻尼吸收的功就是弹性迟滞损失。在旋转过程中，滚动阻力主要来源于胎体的弹性迟滞损失[19]。

根据差速器原理[20]，两侧车轮差速不差扭，即差速器的力学作用是将驱动转矩近似相等地分配给各个车轮。对于采用轮毂电机的车辆，只要控制两侧车轮转矩相等，也可达到类似的差速效果[21]。若对一侧制动力矩进行控制，也可实现车辆自动转向[22]。

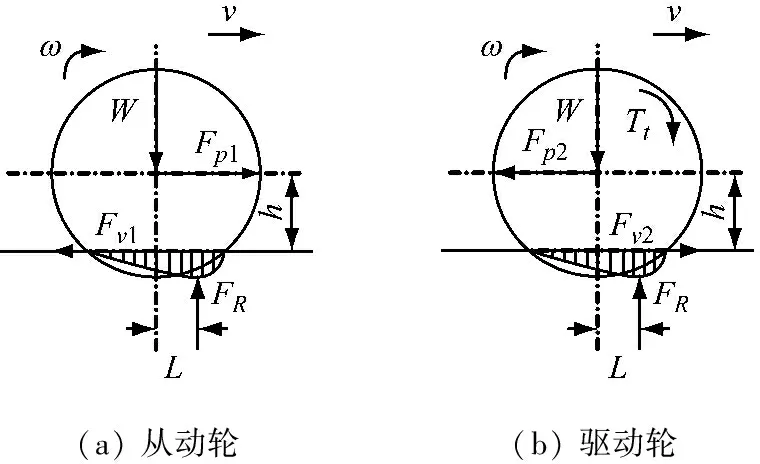
(a) 从动轮(b) 驱动轮

图2 轮胎滚动阻力

Fig.2 Rolling resistance of tire

对于从动轮，作用在轮胎上的力有车轴推力Fp1与地面切向反力Fv1，方向相反；地面法向反力FR和垂向载荷W大小相等，方向相反。有

Fp1-Fv1=G·a

(1)

(2)

式中：h为轮胎有效滚动半径；G为轮胎质量；a为胎心处加速度；L为地面法向反作用力等效着力点偏离胎心的纵向距离，它随弹性迟滞损失的增大而变大；I为轮胎点头转动惯量；ω为轮胎在胎心处滚动角速度。

对于驱动轮，车轮外力增加了驱动力矩车轴Tt，车轴反力Fp2与地面切向反力Fv2，方向与从动轮相反。有

Fp2-Fv2=G·a

(3)

(4)

如图3，车轮刚进入曲线时，外侧车轮有滑拖趋势，即车轮转动线速度小于车轮轮心实际速度，所以位置上落后于弯心O和车轮轴线中心O′连线；内侧车轮有滑转趋势，车轮转动线速度大于车轮轮心实际速度，位置上超前于O-O′连线。差速器的差速原则是最小能耗[23]，即车轮应尽可能远离滑转和滑拖，趋于纯滚动。

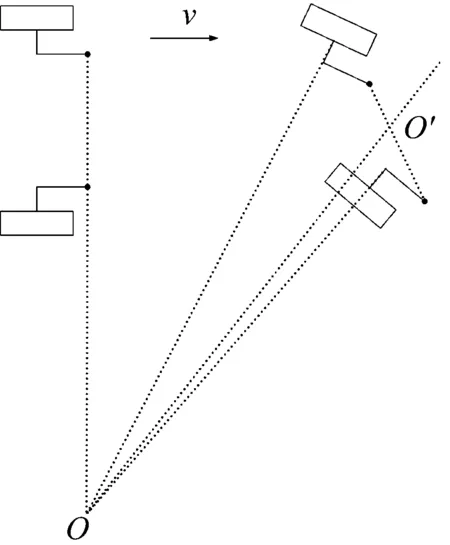
图3 汽车转弯轮胎位置示意图

相对于直线行驶的稳定状态，外侧车轮的滑拖趋势产生与Fv1方向相同的纵向蠕滑力，此蠕滑力使得滚动阻力的合力变小，胎-路接地印记后移[24]，以平衡合力变化，此时L变小；内侧车轮的滑转趋势产生与Fv2方向相同的纵向蠕滑力，此纵向蠕滑力使得滚动阻力的合力增大，胎-路接地印记前移，此时L变大。根据式(1)～(4)，外侧车轮加速旋转，内侧车轮开始减速旋转，直至Fp1增大到

(5)

Fp2减小到

(6)

式中：Ft为作用在车轮上的驱动力。

换言之，对于从动轮来说，地面切向反力加速车轮旋转；对于驱动轮，地面切向反力阻碍车轮旋转。不管是从动轮还是驱动轮，地面法向反力产生的阻力偶矩都是阻碍车轮旋转的，此力偶矩就是轮胎的滚动阻力的根源。外侧车轮的滑拖趋势让FR着力点后移，减小了阻力偶矩，外侧车轮逐渐转得快；同理，内侧转得慢。差速过程在力和力矩平衡时终止，内外轮以不同的速度通过曲线。

1.2 铁道车辆采用机械差速器的可能性

不同于汽车，传统铁道车辆两侧车轮是同轴的，如图4，大半径曲线上，导向轮对横向位移为负，外侧滚动圆半径更大，线速度更大，相对于轮对中心与曲线圆心的连线来说，外侧车轮超前了，有滑转趋势(与汽车内轮一样)，若直接采用汽车上的机械差速器，外侧车轮减速，内侧加速，不利于曲线通过；小半径曲线上，轮对中心线始终达不到纯滚线位置，两侧车轮都是正的横向位移，相对于轮对中心与曲线圆心的连线来说，外侧车轮滞后了(滚动圆半径也是外侧大，但不足以使其超前)，有滑拖趋势(与汽车外轮一样)，可以采用机械差速器。

(a) 大半径(b) 小半径

图4 不同半径曲线上导向轮对的位置示意图

Fig.4 The position of steering wheelset in the curves

考虑轮缘贴靠的情况，大半径曲线上，外侧(滑转趋势)轮缘贴靠，车轮接触点的滑动阻力向前，阻碍车轮旋转，是有害的；小半径曲线上，若外侧(滑拖趋势)轮缘贴靠，车轮接触点的滑动阻力向后，加速车轮旋转，是有益的，若内侧(滑转趋势)轮缘贴靠，阻碍车轮旋转，也是有益的。

所以，对于铁道车辆，若采用机械差速器，应使其在大半径曲线和直线上不作用，在小半径曲线上，差速器作用。

另外，弹性迟滞现象与材料变形程度正相关[25]，钢轮的变形能力远不如橡胶轮胎，即L很小，所以采用机械差速器的作用过程较橡胶轮更慢。

2 基于速差反馈的车辆控制系统模型

2.1 车辆系统动力学模型

本文针对独立车轮轻轨车辆，提出了一种基于速差反馈的直接转速控制方法。

为全面分析曲线通过性能，需考虑车辆系统纵向动力学，因此本文通过大型多体动力学软件SIMPACK 9.8建立了独立车轮城市轻轨车辆整车带驱动控制的动力学模型。计算模型如图5所示，各刚体自由度考虑如下。

车轮：横移，浮沉，侧滚，点头，摇头。

转向架：伸缩，横移，浮沉，侧滚，点头，摇头。

车体：伸缩，横移，浮沉，侧滚，点头，摇头。

由于车轮的浮沉运动不独立，而是伴随横移运动的，所以每车轮实际自由度为4个。车辆系统总自由度DOF=4×8+6×2+6×1=50。

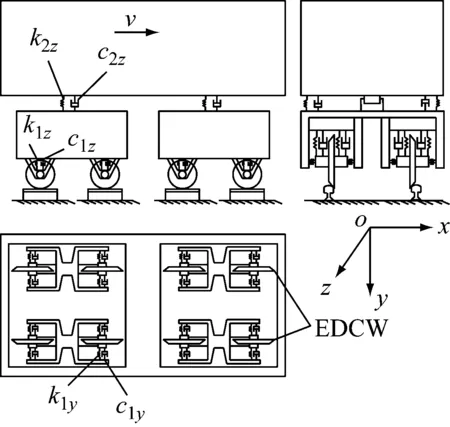
图5 整车动力学模型

本文采用SY8轻轨车轮踏面和59R2槽型轨，轮轨游间10 mm，如图6。独立车轮城市轻轨车辆与汽车共享路权，轨道铺设在公路路面内，为了不侵占平交路口公路车辆的行驶空间，动力学模型中未设置缓和曲线和轨道超高。

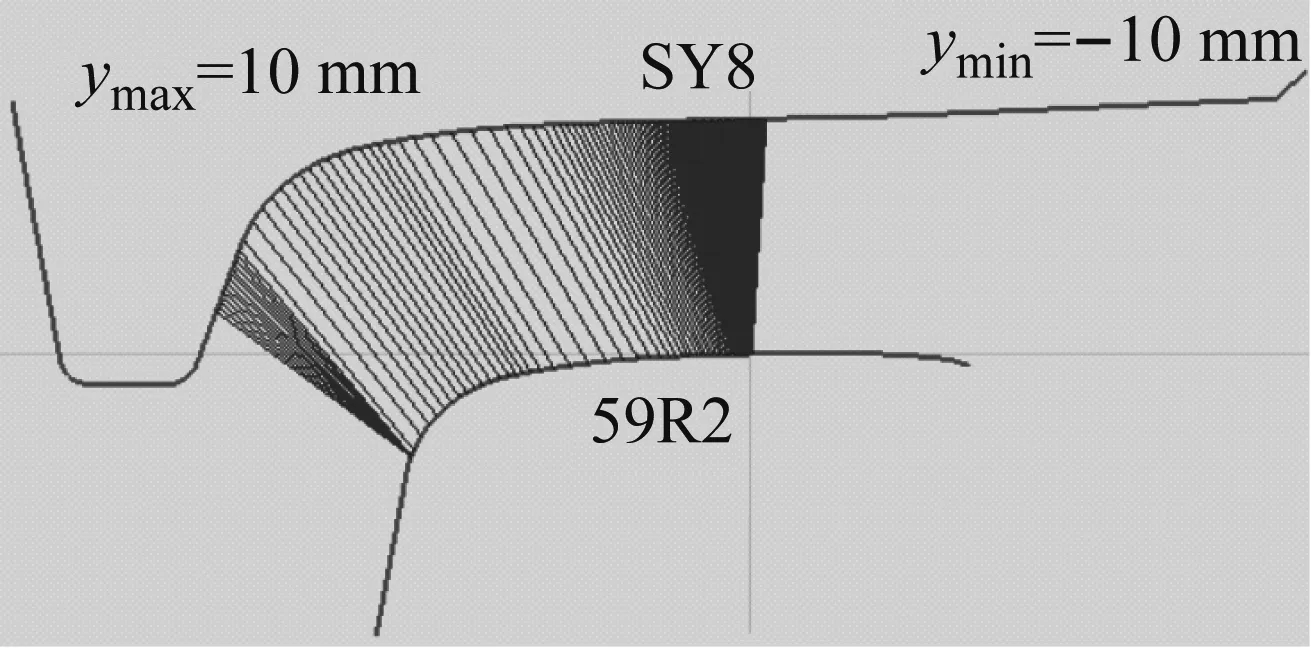
图6 轮轨关系

速差控制轮对的思想是根据左右侧车轮不同的曲线半径，提出不同的转速要求，通过控制模型，实现左右车轮不同的转速。这种耦合方式规避了独立车轮缺乏纵向蠕滑力的缺点，相较于横向耦合轮对和纵向耦合轮对，差速耦合轮对有效减少了轮缘接触风险，尤其适用于小半径曲线。

差速耦合轮对在摇头、横移方向上的运动与独立车轮类似，此处仅列出点头方向的运动方程。

(7)

(8)

式中：b为车轮横向跨距之半；εL、εR为左右车轮点头角；rL、rR为左右车轮滚动圆半径；FxL、FxR为车轮蠕滑力纵向分量；φL、φR为左右车轮摇头角；NzL、NzR为左右车轮法向力垂向分量；ΔT为左右车轮转矩差之半。

2.2 基于速差反馈的控制模型

定义εΔ为左右车轮转速差之半，联立式(7)、(8)得到

(9)

式中:f11为车轮纵向蠕滑率；λ为车轮等效锥度；yw为横移量；φΔ为左右车轮摇头角差之半；v为车速；i表示车轮的左右侧。这些变量都是随车轮位置变化而变化的，可以看出，要控制车轮的转速，最直接的是控制驱动转矩。

当左右车轮转速相等地行驶在曲线上时，忽略车轮摇头角差异，控制的目标极限是

(10)

式(10)的边界条件是车轮横移量yw须小于轮轨游间，再根据轮轨接触点的等效锥度可算得曲线半径分界点Rf。当曲线半径大于Rf时，轮对中心有可能保持在纯滚线；当曲线半径小于Rf时，即使轮缘接触，轮对中心仍不能达到纯滚线位置。

关于独立车轮电机控制技术，现有的计算分析大多假定电机输出为理想状态，未充分考虑电机固有特性。笔者根据现有电机输出能力和机械特性，利用MATLAB/Simulink工具箱设计了一套基于速差反馈的滑模控制系统，并仿真分析了采用该系统的速差控制轮对曲线通过性能。

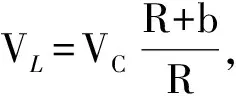
控制系统的三个参数需根据电机特性进行确定，包括驱动转矩、响应时间和监测精度。

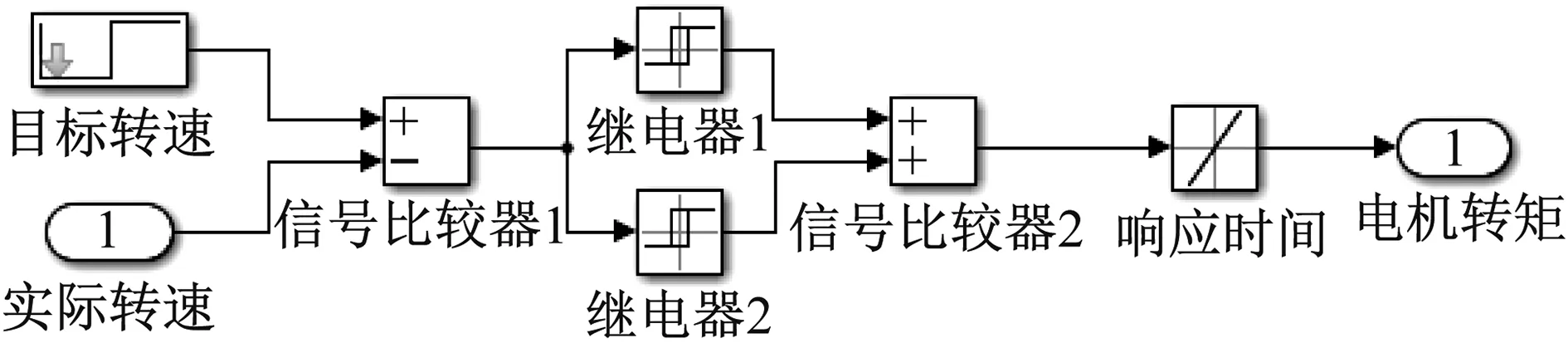
图7 滑模控制系统模型

电机的机械特性对输出转矩影响较大。如图8，在转速达到nb之前，电机转矩恒定，功率上升；在转速超过nb之后，电机转矩下降，功率不变。车辆低速通过曲线时，两侧车轮目标转速不同，控制系统转矩需求较大，而此时电机转矩刚好稳定在较高水平；车辆高速行驶在直线上时，两侧车轮目标转速一样，控制系统转矩需求较小，电机工作在恒功率区间。

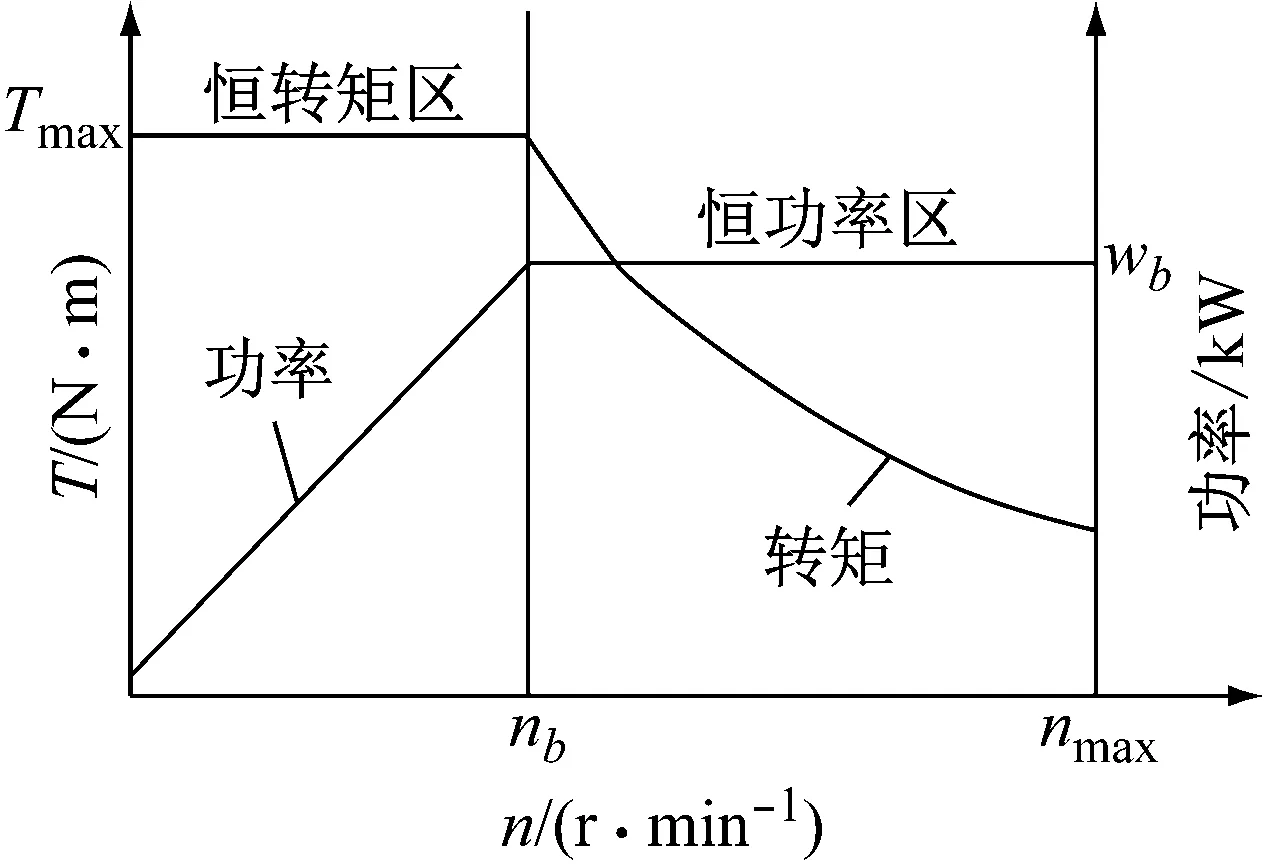
图8 电机转矩特性

为尽量减小电机功率和尺寸，独立车轮城市轻轨车辆采用包含减速器的轮毂电机，选定减速比1∶6。查阅电机选型手册，某型55 kW电机转矩-转速特性如表1。

可以看出，当电机转速不超过1 200 r/min(车速不超过32 km/h)时，电机输出转矩基本稳定在451 N·m左右，取机械传动效率85%，单个车轮的驱动转矩可达到2 300 N·m。响应时间是指当系统未过载时，电机从启动到峰值转矩所需的时间历程，此处取参考值0.1 s[26]。监测精度是指控制器作用的容忍阈值。当车轮实际转速与目标转速差大于此数值时，控制系统介入，继电器输出目标转矩；当转速差小于此数值时，系统默认该差值是电机正常精度误差，控制系统不介入。一般步进电机转速误差可以控制在±0.5%[27]，所以监测精度取0.065 rad/s。

表1 电机转矩-转速特性

继电器1的作用是在车轮实际转速小于目标转速减去监测精度时，释放加速信号；继电器2的作用是在实际转速大于目标转速加上监测精度时，释放减速信号。继电器1、2构成了一个滑模变控制开关，当速度点距离滑模面(目标转速)较远时，电机输出控制转矩，迫使速度点运动到滑模面附近，并在目标转速加减监测精度范围内做滑模运动，有

(11)

式中：n是实际转速；nt是目标转速；m是监测精度；Tεi是作用在车轮上的控制转矩。

3 速差控制轮对曲线通过性能分析

基于前述车辆系统动力学模型和控制系统模型，通过SIMAT联合仿真，对速差控制轮对的轮轨冲角、横向力、脱轨系数、磨耗功等指标进行计算分析。

为对比速差控制轮对对不同半径曲线的适应性，本文采用了差速轮对和同速轮对两种控制方法，差速轮对即曲线上的内外侧车轮目标转速不同，同速轮对即内外侧车轮目标转速始终相等。转速控制结果如图9，同速轮对仅在进、出曲线时有小于0.1 rad/s的转速差，而差速轮对在曲线全段都有1 rad/s左右的转速差，说明该控制系统能有效地控制两侧车轮同速或差速转动，差速转动的目标转速是根据曲线半径算得的，因此，速度差能够保持在稳定、合理范围，不受轮轨黏着系数、轮缘贴靠的影响。

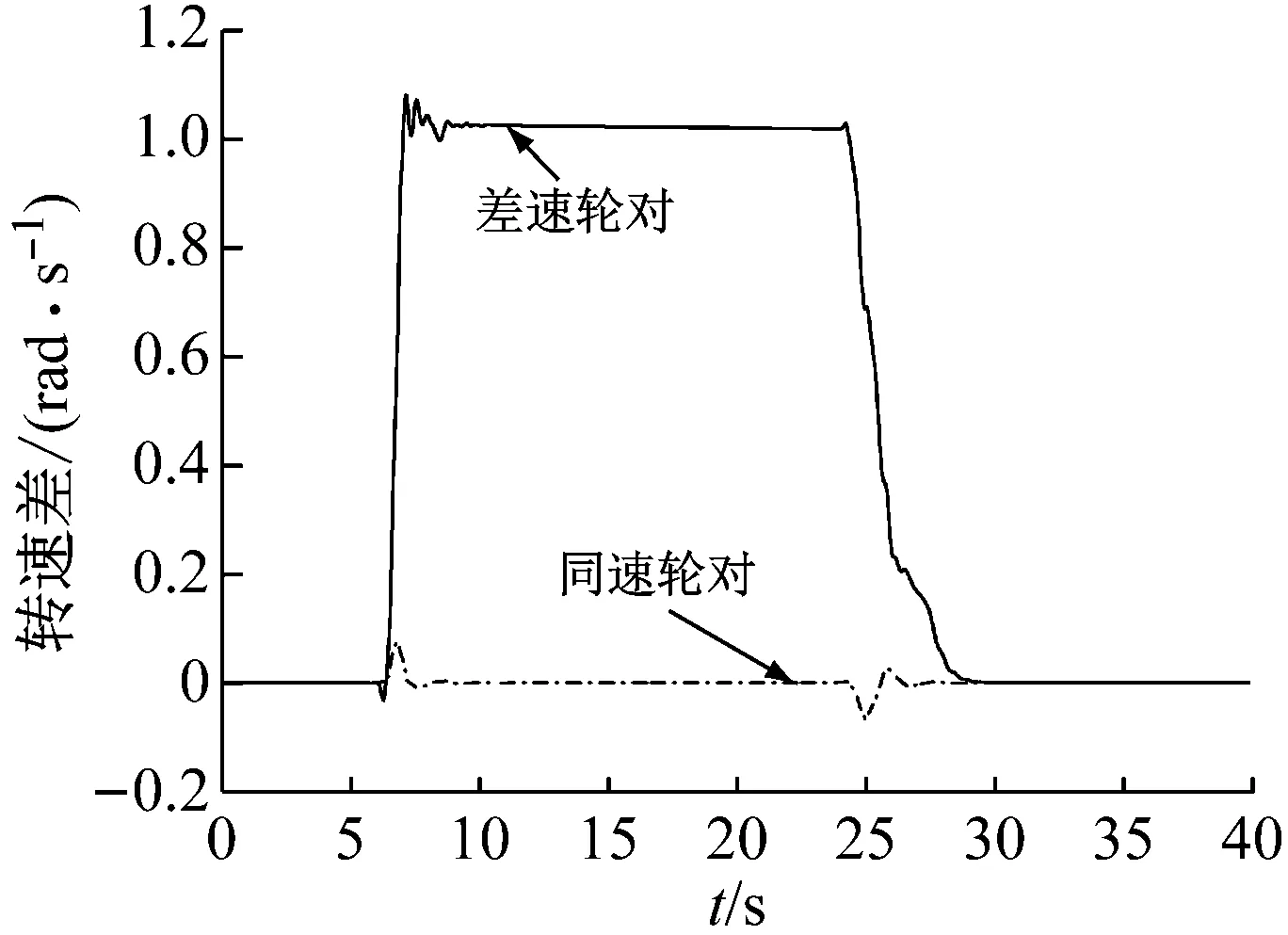
图9 速差控制轮对转速差

仿真线路设置为直线(L=40 m)→圆曲线(L=100 m)→直线(L=200 m)，曲线半径分别为150 m、500 m、850 m。在进入曲线前，车辆从静止加速到20 km/h，然后匀速通过曲线，线路未设置轨道激励。

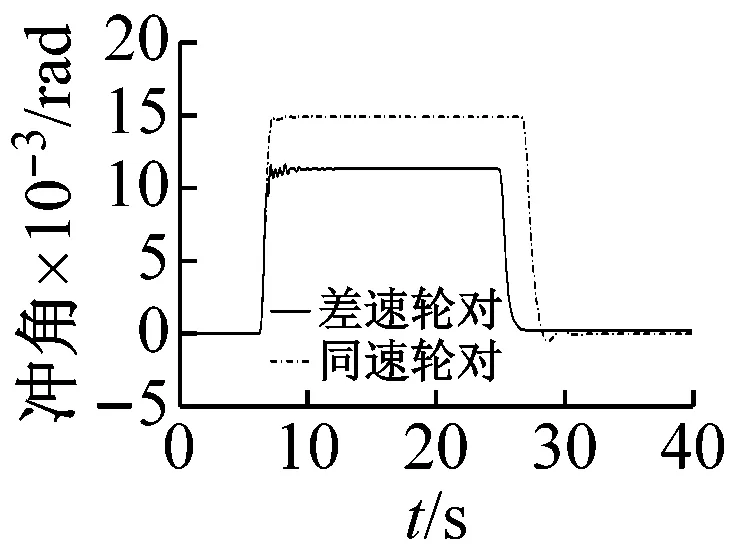
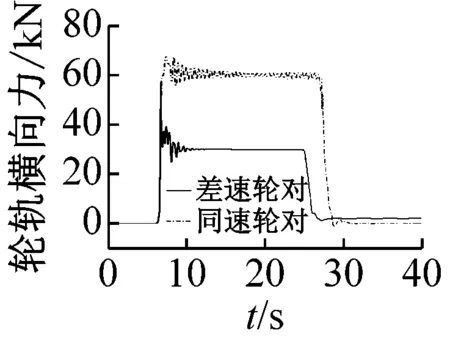
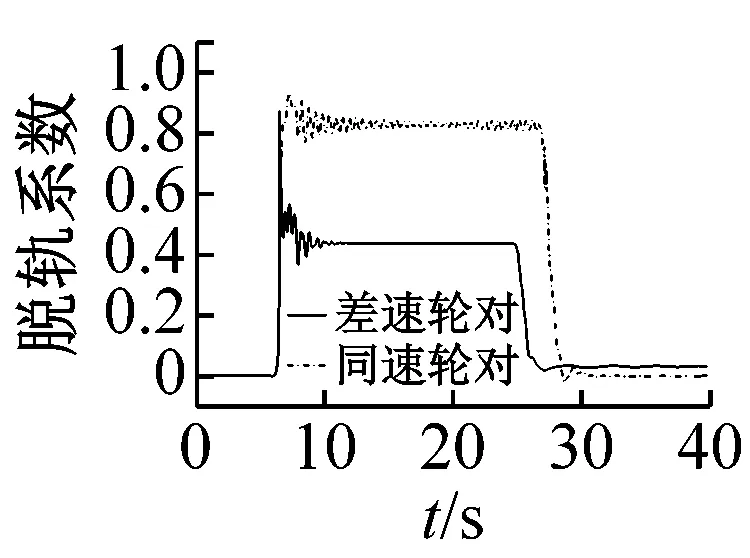
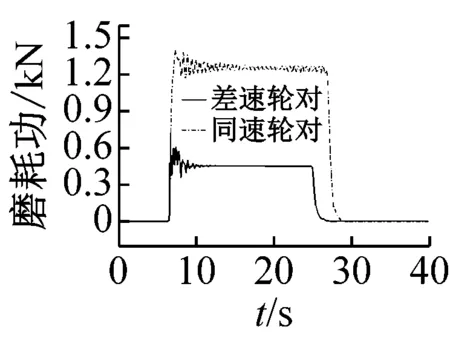
从图10(a)～(c)可以看出，随着曲线半径的增大，导向车轮各指标总体呈下降趋势；通过曲线后，同速轮对出现短暂的蛇行运动而差速轮对没有，说明同速轮对具有耦合轮对的运动特征，差速轮对则更类似于独立车轮；半径150 m曲线上，差速轮对的轮轨冲角、横向力、脱轨系数、磨耗功分别比同速轮对低24%、51%、47%、64%；半径500 m曲线上，差速轮对的轮轨冲角比同速轮对略高，横向力、脱轨系数、磨耗功略低；半径850 m曲线上，同速轮对各指标分别比差速轮对低35%、44%、43%、20%。

(a) R150m

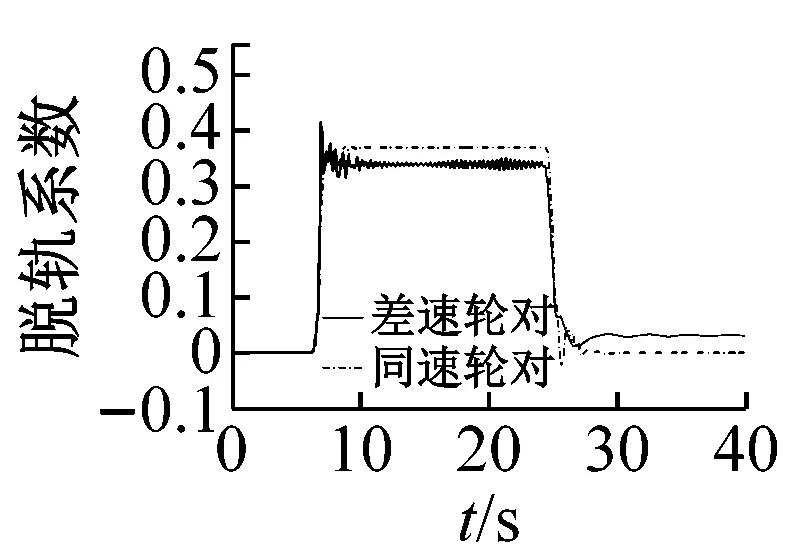
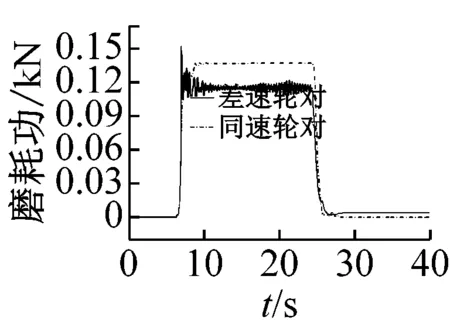
(b) R500m

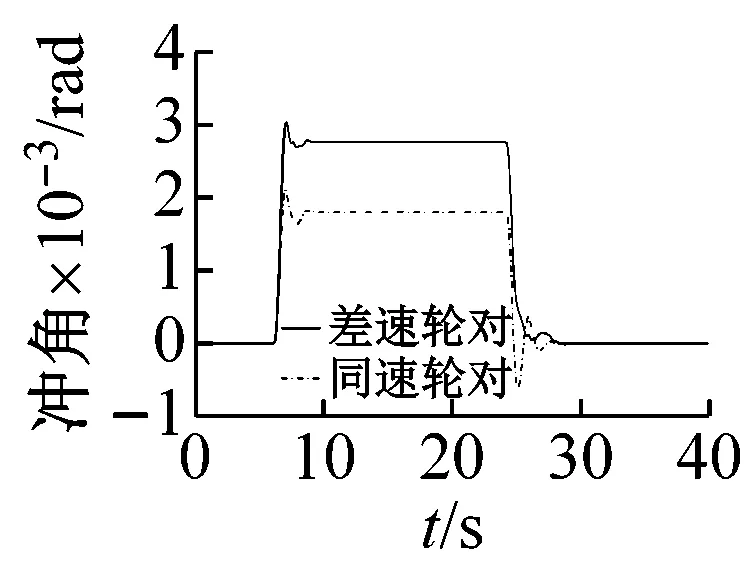
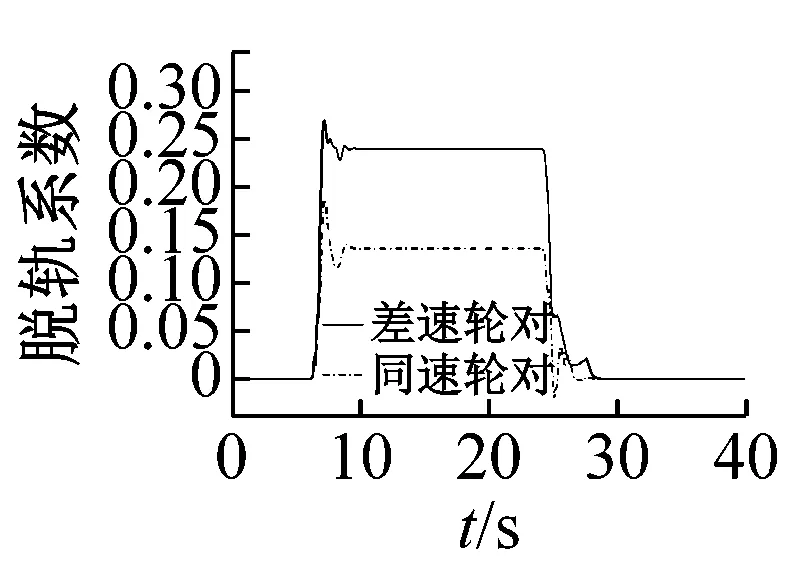
(c) R850m

(a) 冲角

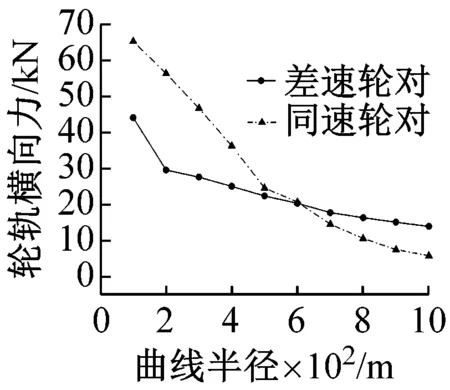
(b) 轮轨横向力

(c) 脱轨系数

(d) 磨耗功

为了找出曲线半径分界点，对更多半径曲线进行了仿真，提取曲线上的指标，见图11。可以看出，随着曲线半径的增大，曲线通过性能指标呈下降趋势。曲线半径在小于500 m时，差速轮对各指标明显低于同速轮对；曲线半径在大于600 m时，同速轮对指标更低；半径在500～600 m时，两种控制方式的车轮曲线通过性能差别不大，说明曲线半径的分界区在500～600 m。

仿真结果说明,独立车轮内外转速差对于曲线通过性能至关重要。小半径曲线上，两侧车轮差速转动有利于减小轮轨冲角、横向力、脱轨系数和磨耗功，曲线通过性能更优；大半径曲线上，两侧车轮同速转动比差速转动更适宜；在中等半径区间，两侧车轮同速转动和差速转动的曲线通过性能差距缩小。曲线半径分界区可从仿真结果直观看出。

本文采用的电差速方案可以大大降低车辆走行系的复杂程度，也规避了机械差速器的弊端。控制系统可以有效地控制车轮同速旋转，以接近耦合轮对在大半径曲线上的自导向性能；也可以控制车轮差速旋转，以接近独立车轮在小半径曲线上的通过性能，并保证转速差在合理范围。

4 结 论

(1) 机械差速过程是基于内外侧车轮不同的滚动阻力实现的，在直线和大半径曲线上，铁道车辆不适宜安装差速器；小半径曲线上，差速器可以正常作用，但差速过程较慢。汽车差速器不能直接移植到铁道车辆上。

(2) R850m曲线上，两侧车轮同速转动较好，轮轨冲角、横向力、脱轨系数和磨耗功相较于差速转动分别降低了35%、44%、43%、20%；R150m曲线上，两侧车轮差速转动较好，各指标相较于同速转动降低了24%、51%、47%、64%；R500～600m曲线上，同速转动和差速转动的车轮曲线通过性能差距缩小直至在此区间内发生交叉互换。

(3) 仿真分析表明，本文采用的控制系统只需根据不同的曲线半径，设置不同的控制目标，即可保证车轮具有较好的曲线通过性能。曲线半径分界区可由理论公式近似算得，也可由仿真得到。大半径曲线上，转速控制目标应为同速转动；小半径曲线上，控制目标应为差速转动。