基于模糊分数阶PID的开关磁阻电机直接瞬时转矩控制

党选举， 彭慧敏， 姜 辉， 伍锡如

(桂林电子科技大学 电子工程与自动化学院， 广西 桂林 541004)

开关磁阻电机(Switched Reluctance Motor, SRM)转子无磁性材料，耗能少，而且结构简单、效率高、调速范围广，因此被广泛应用于航空业、采矿业、家电等领域[1]。但是，SRM具有双凸极结构、非正弦供电、工作在磁饱和非线性区的特点，使SRM在运行时产生较大的转矩脉动[2]，限制了SRM在新能源汽车等特殊场合的应用。因此，SRM转矩脉动抑制的研究一直是国内外的热点。

总体上，SRM转矩脉动抑制的控制方法分为两大类。一类是通过控制SRM的磁链或者电流抑制转矩脉动的间接转矩控制[3-4]；另一类是通过控制SRM的瞬时合成转矩抑制转矩脉动的直接转矩控制[5-6]。然而，工作在磁饱和非线性区的SRM难以建立精确的数学模型，已有常规的控制方法不能有效地抑制SRM转矩脉动。模糊控制不需要被控对象的精确数学模型，实施简洁，易于控制，本质上是一种非线性控制，因此适合应用于SRM转矩脉动控制[7-9]。常用的二维模糊控制器实质上是变参数PD(Proportional Derivative)控制器，由于缺少积分项，系统通常存在静差。

针对二维模糊控制器的缺点，该文将分数阶积分与分数阶微分引入二维模糊控制器设计了一种模糊分数阶PID(Proportional, Integral and Derivative)转速外环控制器用于SRM直接瞬时转矩控制，提高SRM系统的控制性能。MATLAB/Simulink仿真结果表明：基于模糊分数阶PID的SRM直接瞬时转矩控制有效地减小了SRM的转矩脉动，且控制方案易于实现，具有良好的控制性能。

1 SRM直接瞬时转矩控制系统

SRM直接瞬时转矩控制系统采用双闭环控制结构，如图1所示。从图1可知，外环是转速控制，通过转速控制器得到内环参考转矩Tref；内环是转矩控制，实现转矩跟踪控制，从而减小SRM转矩脉动。SRM转速和转矩的变化规律一致[10]，所以控制好转速偏差可以抑制SRM转矩脉动。

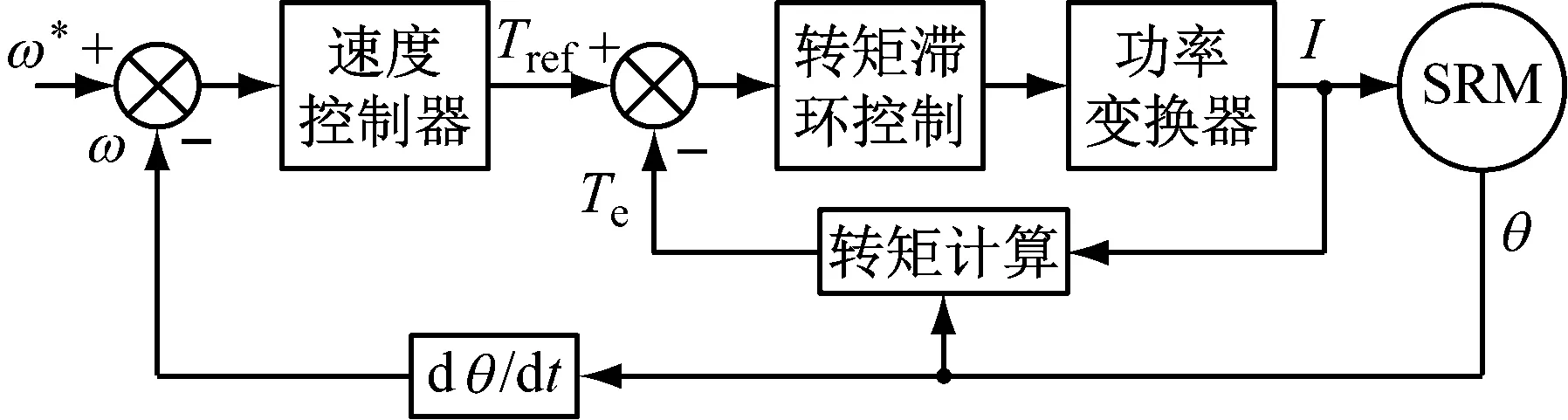
图1 SRM直接瞬时转矩控制系统

SRM直接瞬时转矩控制中功率变换器一般采用三相不对称半桥主电路，控制导通相的不同状态，通过转矩滞环控制器选择适当的换相逻辑，产生各相开关信号以控制输出转矩，达到减小SRM转矩脉动的目的。

2 模糊分数阶PID的SRM直接瞬时转矩控制

该文基于SRM直接瞬时转矩控制策略的基础结构，引入智能控制方法：① 转速外环控制采用设计的模糊分数阶PID控制器对转速进行调节得到转矩内环的参考转矩Tref；② 转矩内环控制采用基于RBF神经网络的PID控制器对转矩进行跟踪调节。基于模糊分数阶PID的SRM直接瞬时转矩控制系统结构，如图2所示。

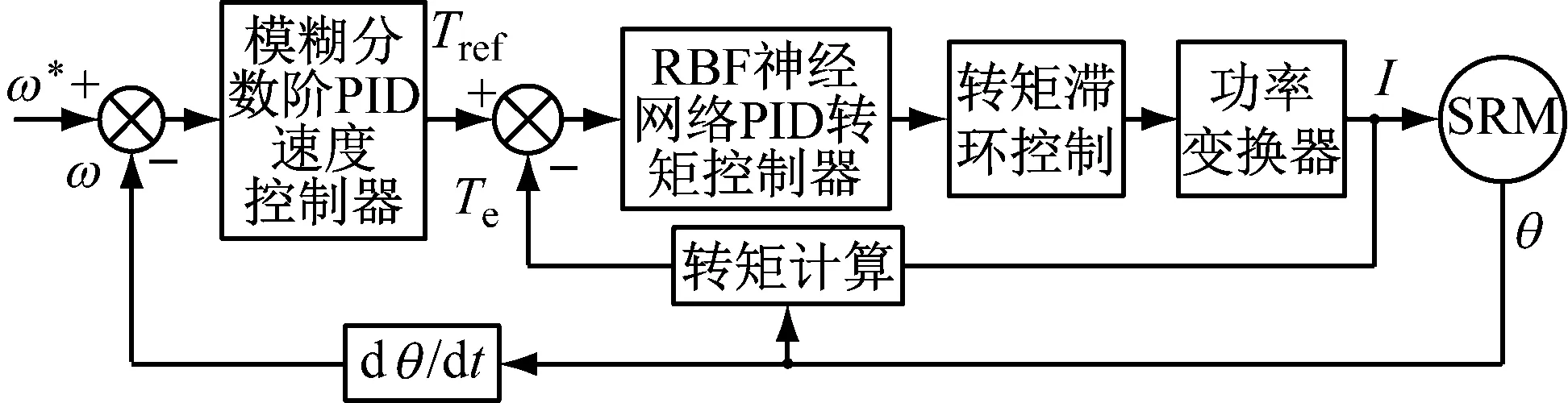
图2 基于模糊分数阶PID的SRM直接瞬时转矩控制系统

2.1 外环转速模糊分数阶PID控制器的设计

2.1.1 分数阶积分与分数阶微分

应用越来越广泛的分数阶积分与分数阶微分[11]是整数阶微积分的阶次从整数到非整数的推广。在控制系统中，应用最广泛的分数阶微积分定义是适于离散化数值估算的解析定义G-L，其定义[12]为

(1)

式中：上标α表示分数阶微积分阶次；下标b和t表示分数阶微积分的上界和下界；j表示分数阶微积分区间均匀划分的子区间标号；h表示区间均匀划分的子区间长度；α>0时，表示分数阶微分；α<0时，表示分数阶积分。

(2)

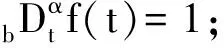
2.1.2 模糊分数阶PID转速外环控制器

为了改善SRM的转矩脉动，该文将分数阶积分与分数阶微分和二维模糊控制器结合，设计了如图3所示的模糊分数阶PID转速外环控制器。图3中点划线部分为引入的分数阶积分和二维模糊控制器并联，虚线部分是引入的分数阶微分代替原有的一阶微分。此时，偏差和偏差的分数阶微分为二维模糊控制器的输入，偏差的分数阶积分和二维模糊控制器并联，因此该控制器具有比例、分数阶微分和分数阶积分的作用，可以作为参数可变的模糊分数阶PID控制器。

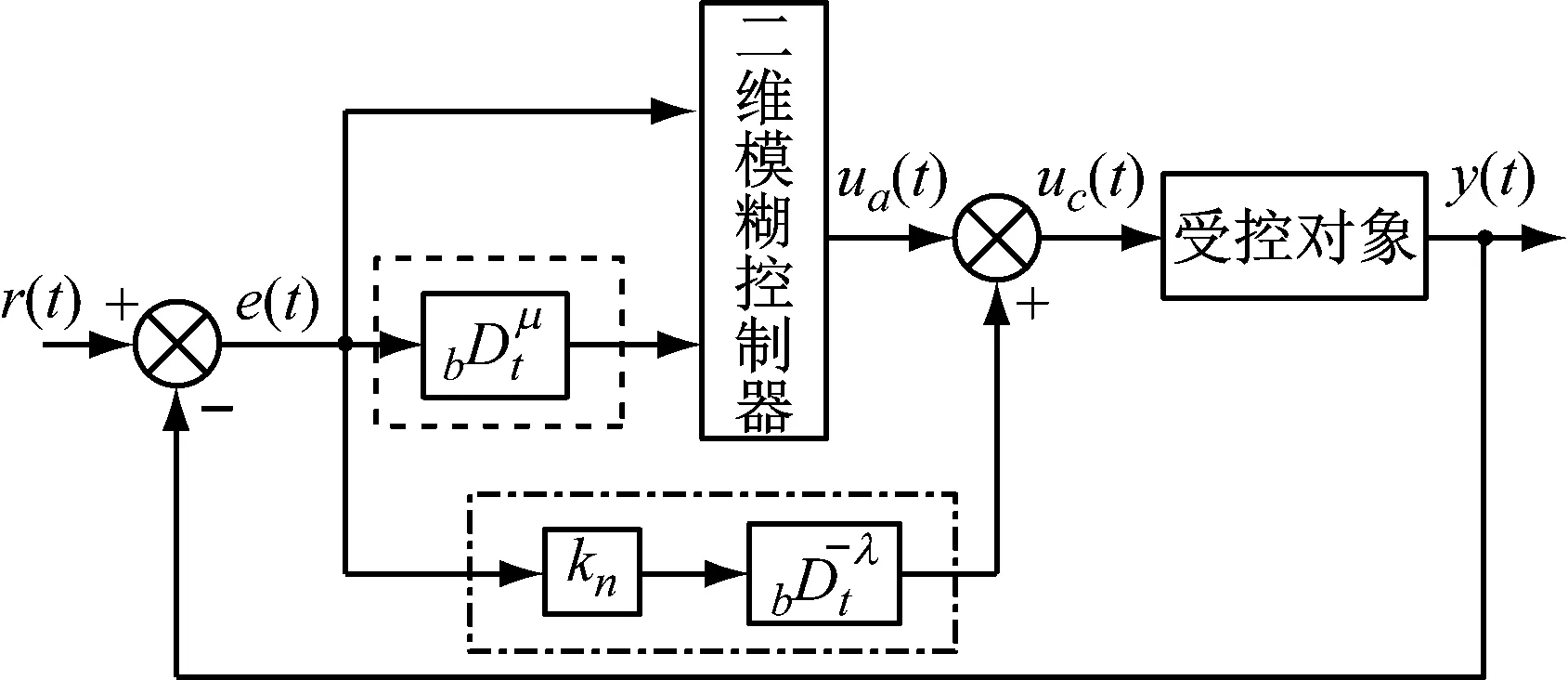
图3 模糊分数阶PID控制器结构框图

引入的分数阶积分和二维模糊控制器并联，对偏差进行分数阶积分提高控制系统的稳态精度，抑制积分饱和作用。由于分数阶微分的记忆特性，使得分数阶微分具有滤波性质，在该文中引入的分数阶微分既可改善控制系统的动态性能，又能削弱一阶微分易受高频干扰的缺点。因此，该文设计的模糊分数阶PID转速外环控制器能提高SRM系统的控制性能。

结合该文被控对象SRM，分数阶积分系数Kn选为Kn=k1+k2/(|e|+k3)，其中k1，k2和k3为常数，|e|为SRM的转速偏差，分数阶积分系数Kn可以依据SRM的转速偏差进行调整，以提高系统的稳态精度。二维模糊控制器的量化因子ke、kec分别相当于模糊分数阶PID的比例系数、分数阶微分系数。

采用最短记忆法实现模糊分数阶PID中分数阶积分与分数阶微分的离散化。把G-L定义的分数阶微积分展开是最简单最直接地应用最短记忆法的离散方法。根据最短记忆法，模糊分数阶PID转速外环控制器中分数阶积分与分数阶微分离散化为

(4)

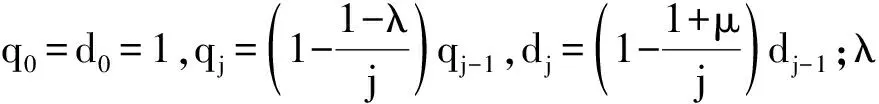
考虑二维模糊控制器算法实现的难易程度和SRM控制精度，选取{NB,NM,NS,ZE,PS,PM,PB}为输入和输出变量，其隶属度函数，如图4所示。

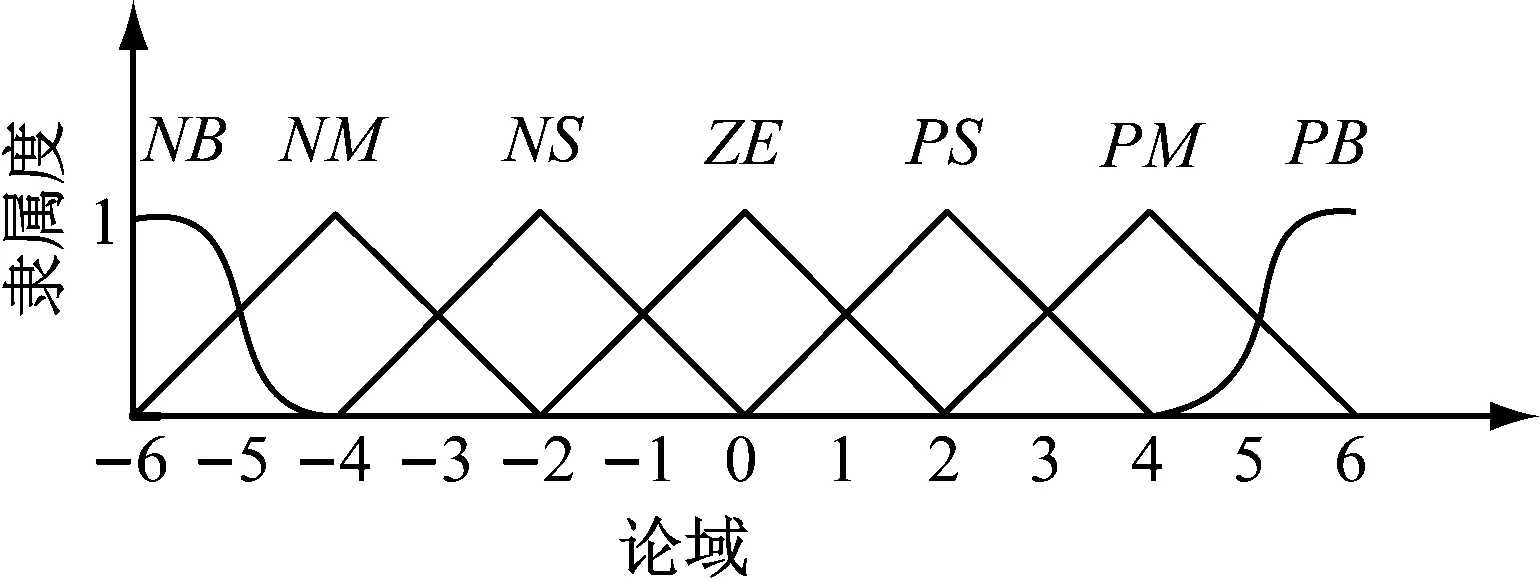
图4 二维模糊控制器隶属度函数

采用Mamdani模糊推理法，利用MATLAB/Simulink对SRM系统多次仿真调试，得到表1所示的模糊控制规则表，其中EC是SRM转速偏差的分数阶微分的模糊集，E是SRM转速偏差的模糊集。

表1 二维模糊控制规则表

2.2 RBF神经网络PID控制内环转矩的设计

为了实现SRM参考转矩Tref的跟踪，该文设计了基于RBF(Radial Basis Function)神经网络的PID内环转矩控制器如图5所示。RBF神经网络以SRM参考转矩Tref和SRM反馈转矩Te偏差的二次型作为PID整定指标，根据SRM转矩偏差的变化调节PID的参数，以适应SRM的非线性。

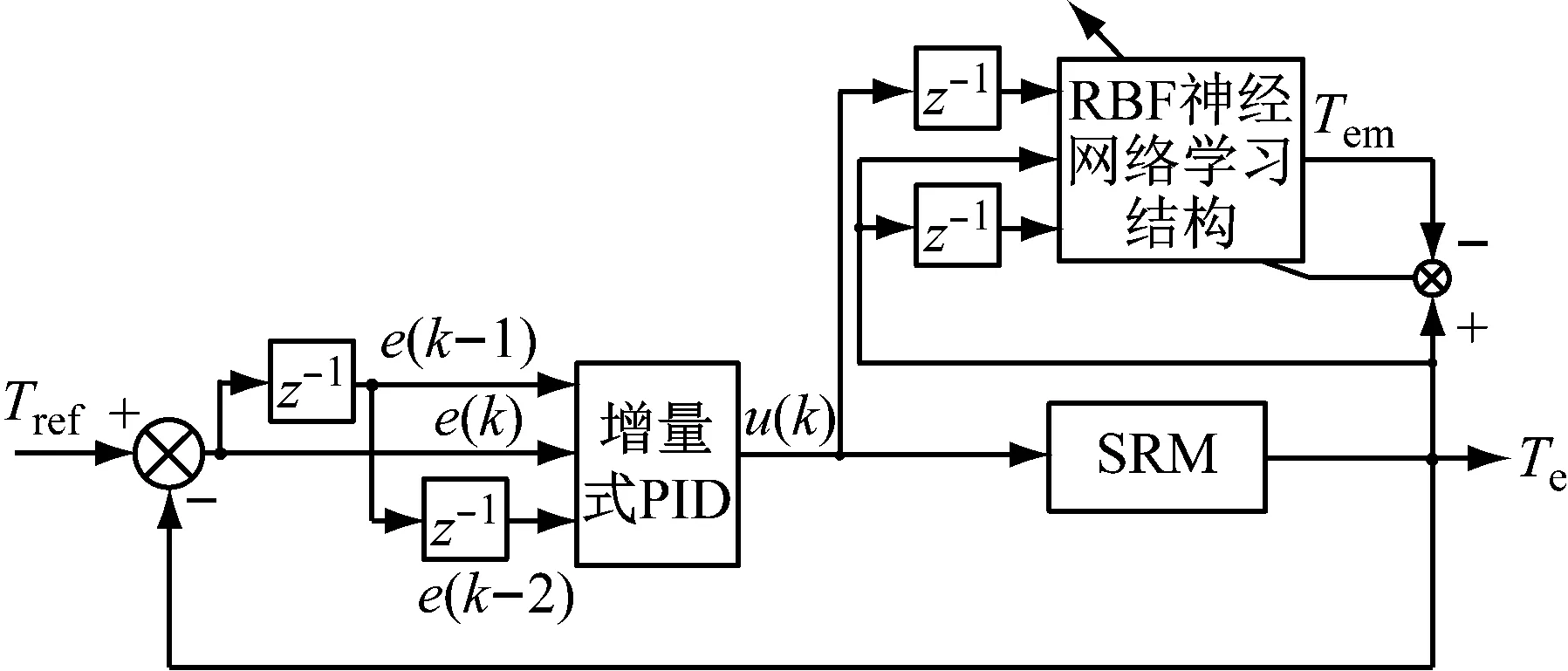
图5 RBF神经网络PID控制结构

增量式PID为

u(k)=u(k-1)+kp(e(k)-e(k-1))+kie(k)+

kd(e(k)-2e(k-1)+e(k-2))=

u(k-1)+kpx(1)+kix(2)+kdx(3)

(5)

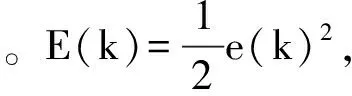
(6)

(7)

(8)

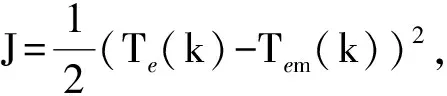
图6 RBF神经网络结构

由梯度下降法，输出层的权值wj(k)，隐含层节点中心cji(k)和基宽参数bj(k)调整算法为

(9)

式中：η为学习速率；α为动量因子。则SRM的Jacobian信息为

(10)

式中：x1=u(k-1)。

3 仿真验证及分析

为了验证该文提出的基于模糊分数阶PID的SRM直接瞬时转矩控制策略的有效性，采用MATLAB/Simulink中的三相6/4极SRM非线性模型仿真验证。引入转矩脉动系数衡量SRM转矩脉动大小，其定义[14]为

(11)

式中:Tmax，Tmin和Tav分别为SRM稳态时的最大瞬时转矩，最小瞬时转矩和平均转矩。

3.1 算法结构分析

模糊分数阶PID速度控制器分数阶积分离散化和分数阶微分离散化所需近似项越多离散化精度越高但所需数据量越大。根据仿真实验情况，考虑离散化精度和系统性能，采样时间T=0.000 1 s，区间标号j取值范围[500,5 000]以优化SRM系统性能。

RBF神经网络PID转矩控制器的隐含层节点影响控制系统的性能，为了确定合理的隐含层节点，采用试凑法和文献[15]提到的隐含层节点优选公式通过多次仿真实验分析确定隐含层节点。基于模糊分数阶PID的SRM直接瞬时转矩控制策略下，通过仿真得到RBF神经网络PID隐含层节点与SRM转矩脉动系数，如表2所示。

从表2可知：隐含层节点由1依次增至6，SRM转矩脉动系数依次减小至1.61%；隐含层节点由7依次增至12，SRM转矩脉动系数大小在1.60%左右；隐含层节点由13依次增至20，SRM转矩脉动系数依次迅速增大。

表2 RBF神经网络PID隐含层节点与转矩脉动系数

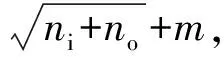
3.2 恒定负载仿真

基于模糊分数阶PID的直接瞬时转矩控制策略中，SRM给定负载TL=8 N·m恒定不变，给定转速w*=150 r/min，进行恒定负载仿真。

根据被控对象SRM的特点，分别改变模糊分数阶PID转速外环控制器的积分阶次λ和微分阶次μ，利用MATLAB/Simulink进行多次仿真调试，探索研究λ和μ对SRM系统的影响，以确定模糊分数阶PID的阶次。

当模糊分数阶PID的分数阶积分阶次0<λ<1时，相当于不完全积分，在一定程度上削弱了积分饱和作用。当SRM系统给定负载转矩发生突变时，模糊分数阶PID的分数阶积分会削弱由积分饱和产生的大超调。因此该文在给定转矩负载突变时，多次仿真调试分析模糊分数阶PID的分数阶积分阶次λ对SRM系统的影响，如表3所示。

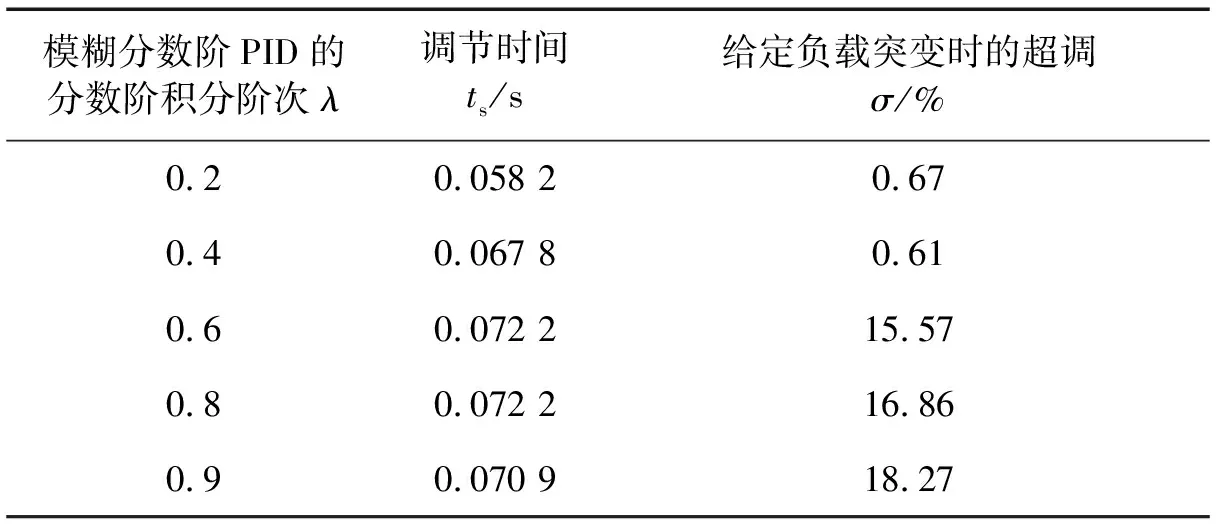
表3 模糊分数阶PID的分数阶积分阶次λ对SRM系统的影响

由表3分析可知，模糊分数阶PID的分数阶积分阶次λ主要影响SRM系统的调节时间，削弱积分饱和引起的大超调。当λ在0.4附近时，调节时间较小，超调较小；当0<λ<0.4时，调节时间变化不大，超调量较小，有效地削弱了由积分饱和引起的大超调；当0.4<λ<1时，调节时间增大，超调增大，SRM系统控制性能较差。

当模糊分数阶PID的分数阶微分阶次0<μ<1时，相当于不完全微分，具有滤波的作用，削弱了一阶微分易受高频干扰的缺点，可以减小SRM的转矩脉动。通过多次仿真调试，分数阶微分阶次μ对SRM系统的影响，如表4所示。

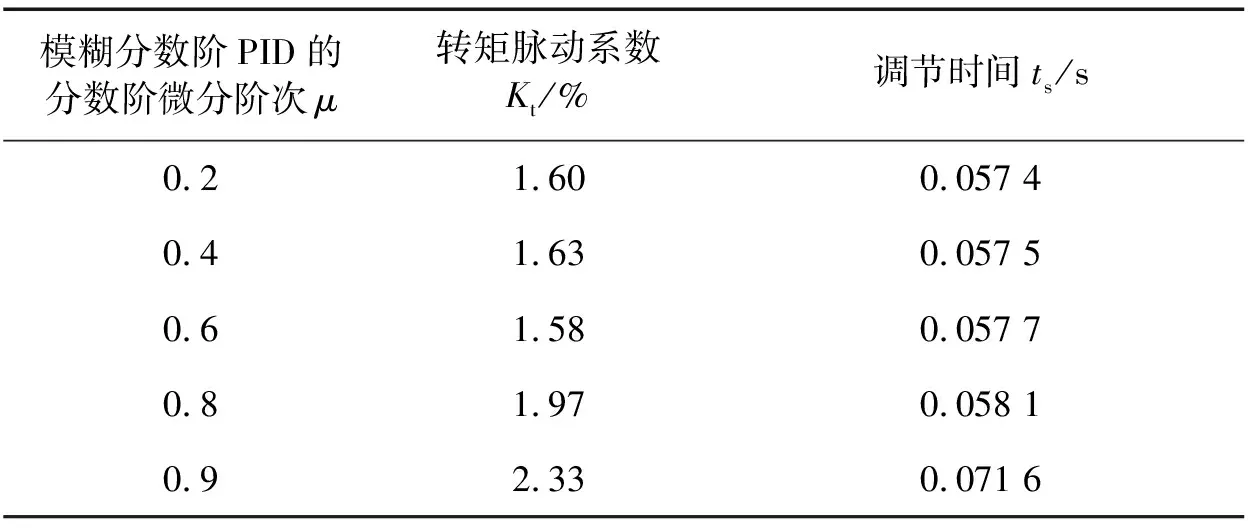
表4 模糊分数阶PID的分数阶微分阶次μ对SRM系统的影响

由表4分析可知，模糊分数阶PID的分数阶微分阶次μ主要影响调节时间和SRM转矩脉动。μ在0.6附近时，转矩脉动较小，调节时间较小；当0<μ<0.6时，转矩脉动在一个较小值附近波动，调节时间变化较小；当0.6<μ<1时，转矩脉动较大，调节时间增大。

通过以上分析，综合考虑模糊分数阶PID的分数阶积分阶次λ和分数阶微分阶次μ对SRM系统的影响，可知模糊分数阶PID的积分阶次在0.4附近，微分阶次在0.6附近时，SRM系统可以获得较好的控制性能，所以选取模糊分数阶PID转速外环控制器的分数阶积分阶次为λ=0.4，分数阶微分阶次为μ=0.6，使SRM系统得到较好的控制性能，基于模糊分数阶PID的SRM直接瞬时转矩控制策略转矩波形，如图7所示。

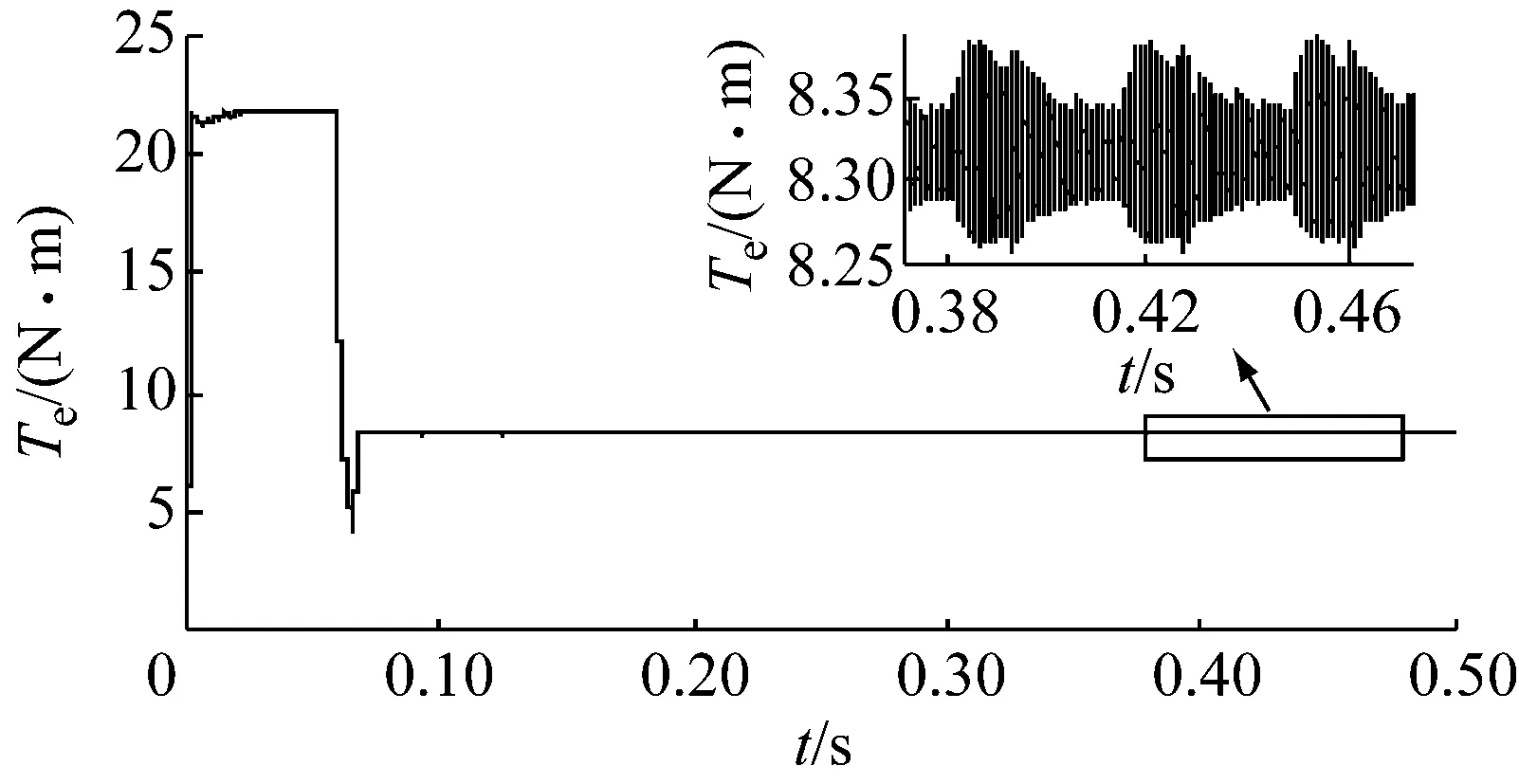
图7 基于模糊分数阶PID的SRM的直接瞬时转矩控制转矩波形图

通过图7可知，在该文提出的基于模糊分数阶PID的SRM直接瞬时转矩控制策略下，SRM的转矩快速达到稳态，且转矩脉动较小。当λ=μ=1时，模糊分数阶PID为常规模糊PID，其它条件不变，基于常规模糊PID的SRM直接瞬时转矩控制策略转矩波形，如图8所示。

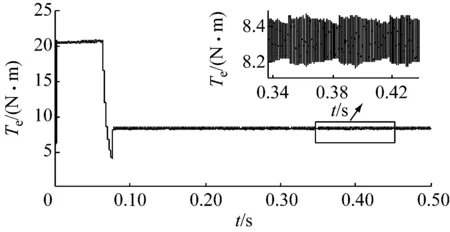
图8 基于常规模糊PID的SRM直接瞬时转矩控制转矩波形图

比较两种控制策略下的SRM转矩脉动系数大小，如表5所示。

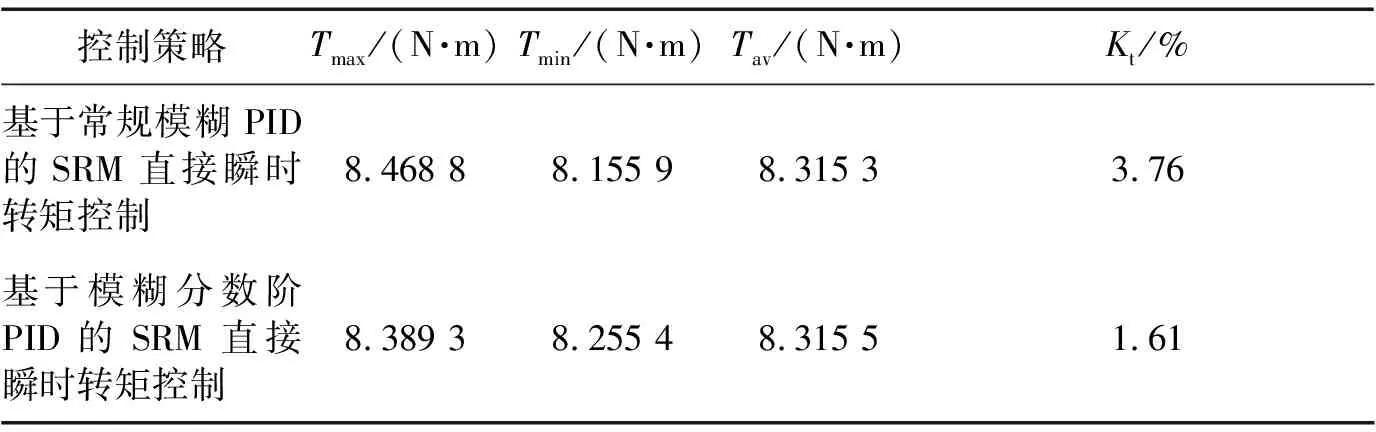
表5 转矩脉动系数比较

从表5中得出，在基于模糊分数阶PID的SRM直接瞬时转矩控制下，转矩脉动系数由3.76%减小到1.61%，表明该文提出的基于模糊分数阶PID的直接瞬时转矩有效抑制了SRM的转矩脉动。

3.3 模拟实际工况仿真

在实际的工作环境中，SRM需要能够实时地适应各种负载工况的变化，以适应在不同的环境下工作。因此该文在仿真时间t=0.35 s时，令SRM负载由8N·m阶跃突变至12 N·m或4 N·m模拟实际工况，分别采用该文提出的基于模糊分数 PID的SRM直接瞬时转矩控制策略和基于常规模糊PID的SRM直接瞬时转矩控制策略对负载的突变进行仿真，用以验证该文所提出控制策略具有很强的适应性，系统在负载突变时可以快速的达到稳态。

两种控制策略下，SRM转矩波形，如图9、图10所示。其中，实线为基于模糊分数阶PID的SRM直接瞬时转矩控制转矩波形，虚线为基于常规模糊PID的SRM直接瞬时转矩控制转矩波形。

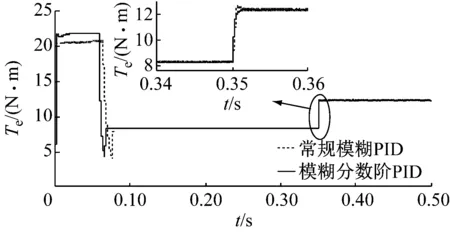
图9 两种控制策略下SRM负载由8 N·m突变到12 N·m转矩波形

Fig.9 The torque waveform of SRM load changed from 8 N·m mutation to 12 N·m under the two control strategies

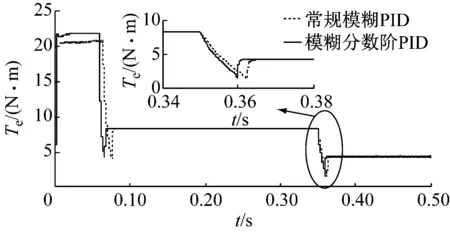
图10 两种控制策略下SRM负载由8 N·m突变到4 N·m转矩波形

Fig.10 The torque waveform of SRM load changed from 8 N·m mutation to 4 N·m under the two control strategies

引入抗扰性能指标恢复时间tv[16]评价负载突变时SRM系统的抗扰性能，负载突变时两种控制策略下恢复时间tv，如表6所示。

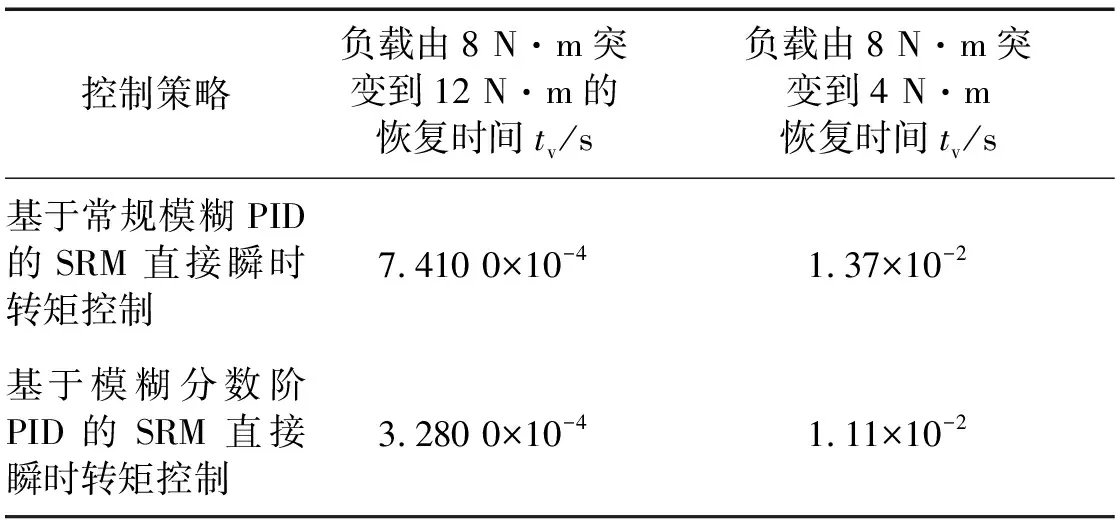
表6 两种控制策略下抗扰性能比较

通过图9、图10和表6可知在负载突然增大或者突然减小的情况下，基于模糊分数阶PID的SRM直接瞬时转矩控制可以迅速的达到稳态，抗扰性能优于基于常规模糊PID的SRM直接瞬时转矩控制。表明该文提出的基于模糊分数阶PID的SRM直接瞬时转矩控制具有很强的适应性，适合在负载突变的实际工况中运行。

4 结 论

在SRM直接瞬时转矩控制上引入分数阶积分与分数阶微分，设计了模糊分数阶PID转速外环控制器，用于调节外环转速。在转矩内环设计了基于RBF神经网络的PID转矩控制器，实现转矩的跟踪控制，从而减小SRM转矩脉动。通过仿真分析探讨研究了模糊分数阶PID转速外环控制器的分数阶积分阶次λ和分数阶微分阶次μ对SRM系统的影响，表明设计的模糊分数阶PID转速外环控制器不仅可以削弱积分饱和引起的大超调，而且有效地解决了一阶微分易受高频干扰的缺点，提高了系统的动态性能。仿真结果表明：提出的基于模糊分数阶PID的SRM直接瞬时转矩控制策略对给定的参考转矩Tref能够跟踪控制，且转矩可以快速地达到稳态，稳态时转矩脉动小；负载转矩突然增大或者突然减小时均能快速达到稳态适应于实际工况，验证了该文提出的基于模糊分数阶PID的SRM直接瞬时转矩控制策略对SRM转矩脉动抑制的有效性和适应性。