三参数离散灰色预测模型DGM(1,1)3及其应用
2018-12-21周雪玉
孙 峰,周雪玉
(重庆工商大学a.旅游与国土资源学院;b.国家智能制造服务国际科技合作基地,重庆 400067)
0 引言
灰色预测模型[1]是研究和解决小数据不确定性问题的一种常用方法。经过三十余年的发展,灰色预测模型已由最初的GM(1,1)模型拓展出GM(1,N)模型、DGM(1,1)模型、Verhulst模型、DGM(2,1)模型[2-4]等;建模对象也由最初的实数序列拓展至区间灰数序列、离散灰数序列及灰色异构数据序列[5-8]。上述研究成果的不断涌现,丰富了灰色预测模型理论体系,改善了灰色预测模型的建模能力与适用范围,促进了灰色预测模型与现实问题的有效对接,解决了生产和生活中的大量实际问题。
谢乃明对经典GM(1,1)模型进行了非常深入的研究,认为GM(1,1)模型中利用离散形式的差分方程进行参数估计,利用连续形式的微分方程进行拟合和预测,而离散形式和连续形式由于构造方式不同是不能精确等同的,这两种形式之间的跳跃是造成模型误差的根本原因,在此基础上提出了离散灰色预测模型DGM(1,1)[9,10]。DGM(1,1)解决了经典GM(1,1)无法实现齐次指数序列无偏拟合的不足,在灰色预测模型体系中具有十分重要的地位。
为了进一步优化DGM(1,1)模型的模拟及预测精度,研究人员从初始值、背景值、累加阶数、非齐次序列模拟、模型性质、区间DGM(1,1)模型等方面[11-15]对DGM(1,1)进行了大量研究,促进了该模型的发展和完善。然而,当建模序列具有一定的波动性特征时,传统的DGM(1,1)及其优化模型,其模型精度仍然较差。这主要是因为DGM(1,1)在建模时,仅考虑了β1(k) 对x̂(1)(k+1) 的影响,当β1(k)为异常值并导致序列呈现出波动特征时,将直接对(k+1)的模拟及预测值造成干扰,导致模型精度不理想。这就是DGM(1,1)模型在面对具有一定波动特征的建模序列时,即使其参数最优而预测效果仍不理想的根本原因。
本文在传统DGM(1,1)的基础上,提出了一种三参数的离散灰色预测模型(简称DGM(1,1)3模型),该模型充分考虑了序列滞后项对模拟及预测结果的影响,能在一定程度上改善建模序列光滑性,较好地规避了序列中的极端奇异值对的模拟及预测值可能造成的干扰,从而提高离散灰色预测模型性能。本文通过对波动序列模拟及预测误差的比较和分析,验证了DGM(1,1)3模型具有比传统的DGM(1,1)及经典GM(1,1)更好地模拟及预测性能。最后将该模型成功地应用于安徽省万人有效发明专利数的模拟及预测。
1 DGM(1,1)3模型
1.1 DGM(1,1)3模型的定义
定义1:设非负原始数据序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n) ),其中x(0)(k)≥0,k=1,2,…n,序列X(1)是序列X(0)1-AGO[2]序列,即:

其中:

则:

被称为是含参数β1,β2及β3的离散灰色预测模型,简称DGM(1,1)3模型。在该模型中,x(1)(1)及x(1)(2)被称为DGM(1,1)3模型的初始值。显然,当β2=0,DGM(1,1)3模型即为传统的DGM(1,1)模型。
1.2 DGM(1,1)3模型的参数估计
本文将应用最小二乘法(OLS)及克莱姆法则来估计DGM(1,1)3模型的参数β1,β2及β3。确保x(1)(k+1)的模拟值x̂(1)(k+1)最小模拟误差S需满足:

根据最小二乘法,可得:

则:

根据克莱姆法则,可得:
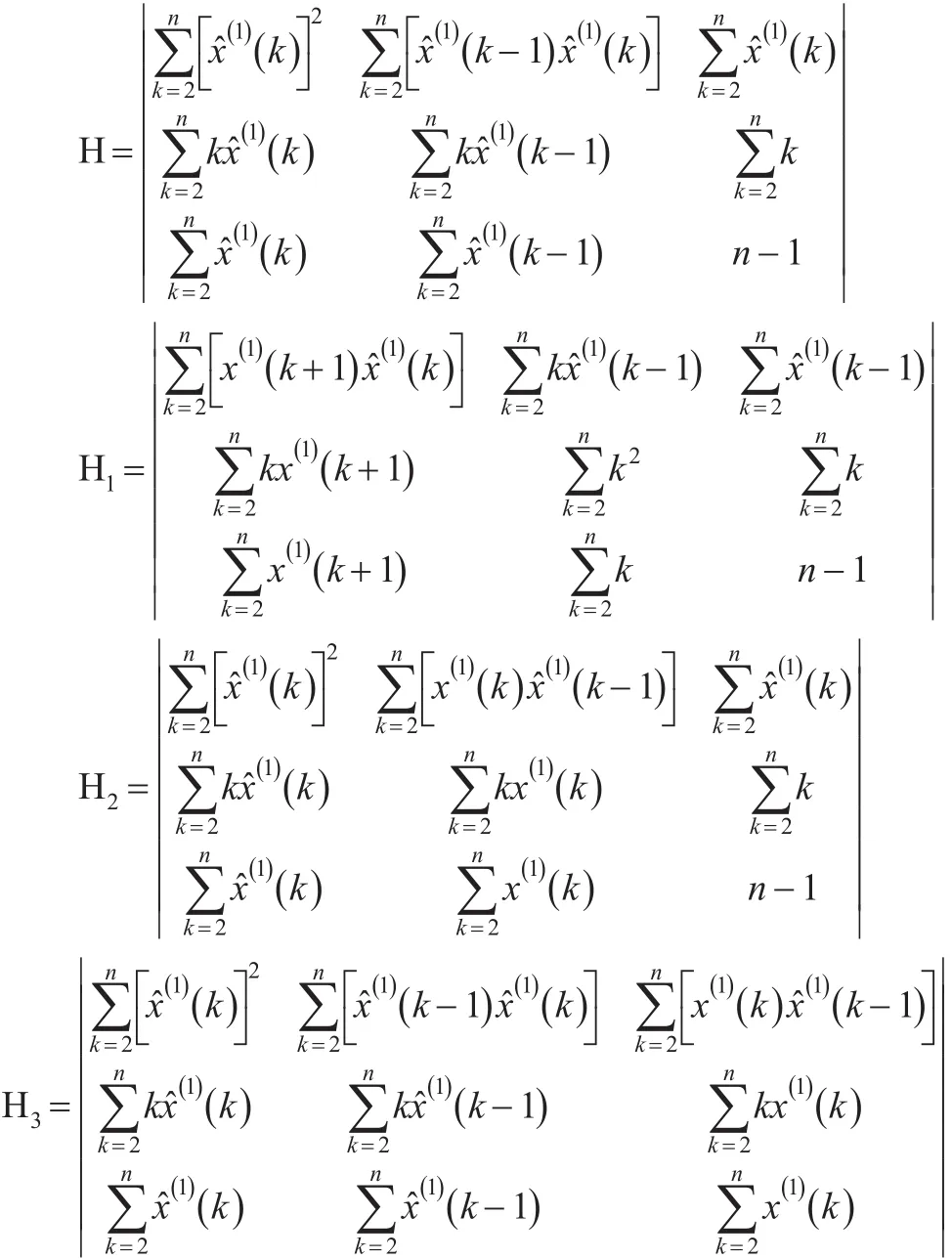
参数β1,β2及β3的计算表达式,如下:

1.3 DGM(1,1)3模型的推导
根据定义1,当k=2:

当k=3:
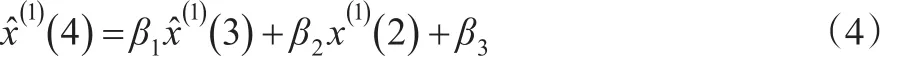
将公式(3)带入公式(4),得:

当k=4:

将公式(4)、公式(5)带入公式(6),得:

从上面的推导过程可以发现,DGM(1,1)3模型的时间响应函数的推导过程是非常复杂的,很难发现其演变规律。实际上,本文构建DGM(1,1)3模型的目的是模拟或预测数据(k) 及(k),k=2,3,…,4,在这个意义上而言,DGM(1,1)3模型的时间响应式并不重要。根据定义1可知,DGM(1,1)3模型满足迭代算法,因此可以通过一个MATLAB程序来实现数据(k) 的计算,在此基础上,根据累加生成的逆过程求解最终还原值(k)。
2 模型性能比较和分析
设随机序列X(0)(x(0)(1),x(0)(2),…,x(0)(n)),其中40≤x(0)(k)≤80,k=1,2,…,n。分别构建序列X(0)DGM(1,1)3模型,DGM(1,1)模型及GM(1,1)模型,并对上述三个模型对序列X(0)的模拟及预测误差进行比较和分析。

为了同时比较不同模型的模拟及预测性能,本文将随机序列X(0)分成两个部分。其中,第一部分(k=1,2,…,10)用来建立DGM(1,1)3模型,DGM(1,1)模型及GM(1,1)模型,并计算模型模拟误差;第二部分(k=11,12,…,15)用来测试模型的预测性能。
运用MATLAB软件计算各模型参数,结果如下所示:
(1)DGM(1,1)3模 型 :β1=1.5969;β2=-0.5710;β3=22.6016
(2)DGM(1,1)模型:β1=1.0884;β2=35.6882
(3)GM(1,1)模型:a=-0.0854;b=33.9309
根据模型的参数,可计算上述三个模型对随机序列X(0)(k=1,2,…,10)的模拟值及模拟误差,计算结果如表1所示。
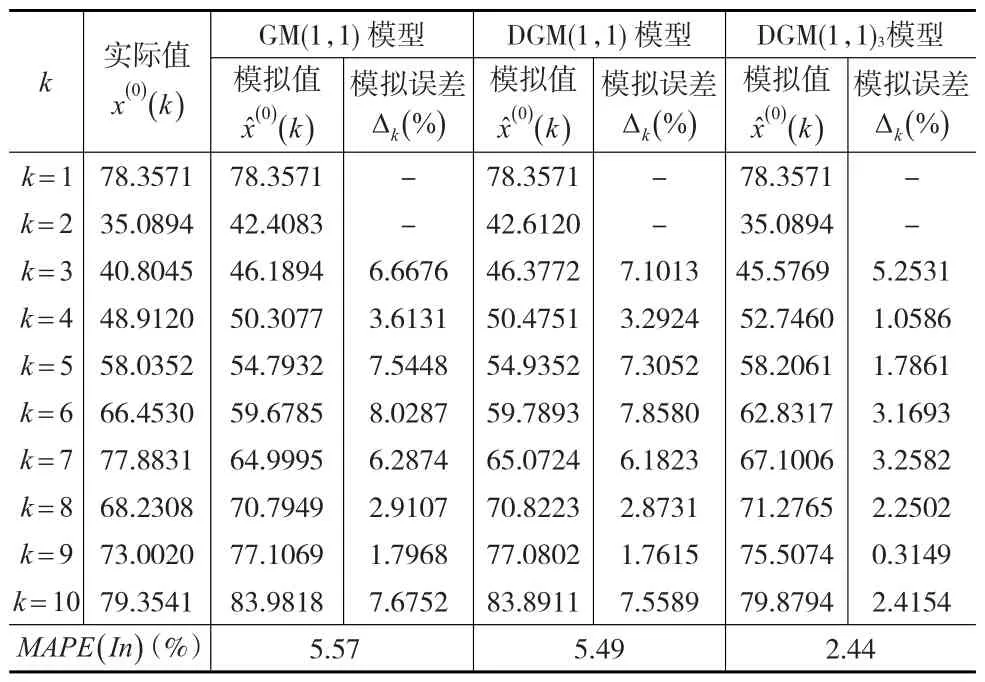
表1 GM(1,1)、DGM(1,1)及DGM(1,1)对随机序列 X(0) 的模拟值及模拟误差3
类似地,当k=11,12,…,15时,可以计算三个模型对随机序列X(0)的预测值及预测误差,结果如表2所示。
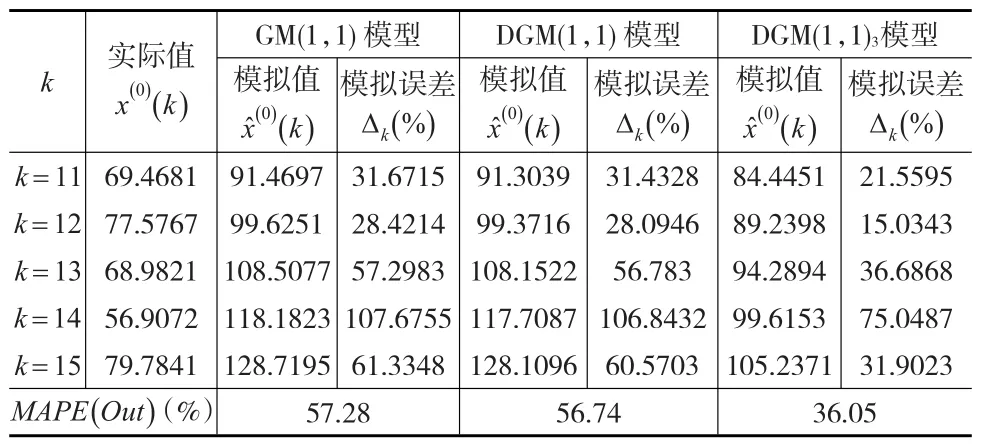
表2 GM(1,1)、DGM(1,1)及DGM(1,1)对随机序列 X(0) 的预测值及预测误差3
在表1及表2中,符号x(0)(k),x̂(0)(k),Δk(%),MAPE(In) andMAPE(Out)含义如下:
(1)x(0)(k)序列X(0)的第k个元素。
(2)x̂(0)(k)对应x(0)(k)的模拟或预测值。
(3)Δkx̂(0)(k)的模拟或预测绝对百分误差。
(4)MAPE(In)平均绝对模拟百分误差。
(5)MAPE(O ut)平均绝对预测百分误差。
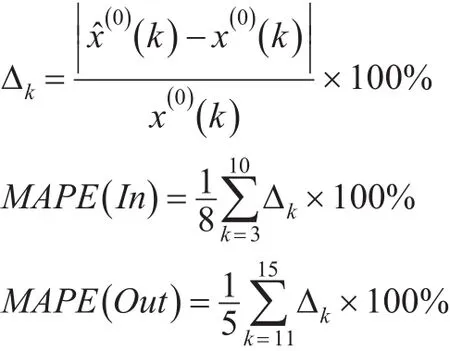
根据表1、表2不难发现,相对于GM(1,1)与DGM(1,1),本文所构建的DGM(1,1)3对随机序列X(0),其模拟及预测误差最小,这表明对于相同序列,DGM(1,1)3具有相对更优的模拟及预测性能。这主要是因为在DGM(1,1)3模型中增加了滞后项β2x(1)(k-1),表示x(1)(k+1)的值不仅仅受到β1x(1)(k)的影响,同时还受到滞后项β2x(1)(k-1)的影响,从而避免了β1x(1)(k)的极端值对x(1)(k+1)可能产生的冲击,起到了抑制极端值及改善序列平滑性的效果。
3 模型应用
万人有效发明专利数是指每万人拥有经国内外知识产权行政部门授权且在有效期内的发明专利件数,是衡量一个国家或地区科研产出质量和市场应用水平的国际通用综合指标,主要体现一个国家或地区自主科技创新能力。安徽省2010—2015年的万人有效发明专利数,如表3所示(数据来自《安徽省统计年鉴》)。本文将构建安徽省万人有效发明专利数的DGM(1,1)3模型,并对该省2016—2020年的万人有效发明专利数进行预测。

表3 安徽省2010—2015年万人有效发明专利数 (单位:件)
根据表3可知:
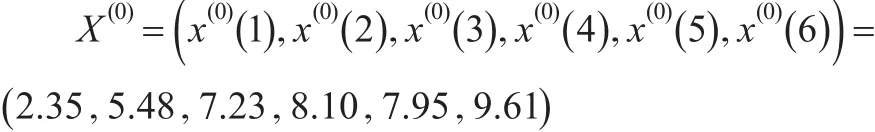
则序列X(0)的1-AGO序列X(1)为:

应用MATLAB程序可计算序列X(0)的DGM(1,1)3模型,如下:


则安徽省万人有效发明专利数的DGM(1,1)3模型为:应用公式(8),可计算安徽省2010—2015年万人有效发明专利数的模拟值及模拟误差:

则:

根据灰色预测模型误差等级参照表[2],可知该模型的误差等级为II,可用于中短期预测。
根据公式(8),预测安徽省2016—2020年万人有效发明专利数,结果如表4所示。

表4 安徽省2016—2020年万人有效发明专利数 (单位:件)
根据表4可知,安徽省2016—2020年万人有效发明专利数预计呈现快速增长的趋势,到2020年,其数据规模将达到14.71件,是2010年的6倍多。这主要得益于近年来安徽省大力推进科技创新型省份的建设,出台了支持科技创新的“1+6”政策和“1+10”政策。扶持高层次科技人才团队在皖创新创业、促进科技成果转化、大型科学仪器共享共用、市创新能力评价5项实施细则,同时研究制定科技重大专项、科技保险试点、实验室建设、专利权质押贷款4项实施细则,加上已出台的高新技术产业投资基金实施细则,形成覆盖创新驱动全过程的“1+10”政策体系。
4 结论
本文在传统DGM(1,1)的基础上,提出了一种三参数的离散灰色预测模型DGM(1,1)3,该模型充分考虑了序列滞后项对模拟及预测结果的影响,能在一定程度上改善建模序列光滑性,较好地规避了序列中的极端奇异值对(k+1)的模拟及预测值可能造成的干扰,从而提高离散灰色预测模型性能。通过对波动序列模拟及预测误差的比较和分析,验证了DGM(1,1)3模型具有比传统DGM(1,1)及经典GM(1,1)更好的模拟及预测性能。最后将该模型成功地应用于安徽省万人有效发明专利数的模拟及预测。如何对DGM(1,1)3模型的初始条件、背景值、建模条件、累加阶数等内容进行系统研究,是项目组下一步的将要研究的主要内容。
