基于D-DEA交叉效率的混合型多属性决策方法

张兴贤，王应明

（1.福州大学 决策科学研究所，福州 350116；2.铜陵学院 建筑工程学院，安徽 铜陵 244061）

0 引言

目前，针对这类含有投入产出指标的混合型多属性决策问题已有学者进行了有益的探索，相关研究成果大致分为两类:第1类是将模糊综合评价（FCA）和数据包络分析（DEA）两种方法相结合，提出了不同类型的混合型多属性决策方法[1-3]，第2类是将证据理论（DST）和数据包络分析（DEA）两种方法相结合，提出一种基于证据理论与DEA交叉效率的决策评价方法[4,5]。

上述两类决策方法在一定程度上解决了混合型多属性决策问题，但这两类方法仍然存在某些不足:第1类方法考虑了在语言评估中的模糊性，但是不能融合多个专家的判断结果来提高评估结果的客观性。第2类方法通过融合多个专家的评估结果来降低专家评估的主观性，但是没有考虑在语言评估中的模糊性。换言之，证据理论假设识别框架中的元素必须是相互排斥的。然而，在语言评价中，语言等级如“不好”，“一般”和“好”并不能完全满足这个要求。

为了结合上述两类方法的优点，本文引入D数理论[6]，D数理论作为证据理论的扩展，因其识别框架非排斥性的假设而广泛用于语言评价中[7，8]。将D数理论与数据包络分析两种方法相结合能很好地克服上述两类方法的缺陷。

1 预备知识

1.1 DEA交叉评价方法

假设有n个决策单元（DMU）需要评估，每个评价单元均有m中投入和s种产出，对于第k个决策单元DMUk(k=1，2，…，n)，用χpk(p=1，2，…，m)表示DMUk的第p种投入量，用yrk表示DMUk的第r种产出量。在CCR模型下，对于任意第d个决策单元DMUd，利用下式计算得到最优效率值Edd和投入产出指标的最优权重，（μ*rd，ω*pd）[9]:

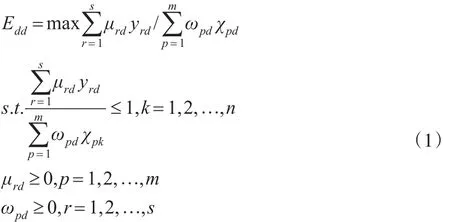
根据交叉评价思想，通过下式计算得到其他决策单元DMUk相对于这个决策单元的交叉效率：

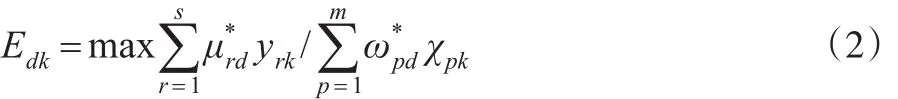
从而得到交叉效率评价矩阵E，通过集结矩阵中交叉效率值可实现对决策单元的充分评价。针对交叉效率评价中还可能存在多重最优解问题，可采用压它型策略或利众型策略来消除交叉效率不唯一的问题。

1.2 证据理论

Dempster-Shafer理论（DST）[10]简称证据理论用来处理不确定信息。该理论最早由Dempster提出并由Shafer进一步发展。该理论需要弱化概率论的条件，因此被认为是概率论的扩展。作为一种不确定环境下的推理理论，证据理论拥有对多个目标构成的集合的子集分配概率来直接表达不确定性的优势，而不是直接分配给个体目标。分配到每个子集的概率有上下限，分别表示测度子集总的信度函数和似真函数。此外，证据理论还能融合多个证据。

1.2.1 基本概念

定义1：设H为互不相容的基本命题（假定）组成的完备结合，H={H1,H2,….Hn}为一个识别框架（Frame of Discernment），2H为H的幂集：

2H={∅，{H1},…{HN}，{H1，H2},…，{HN-1，HN},…{H1,…,HN}}，如果A∈2H，A称为识别框架H中的一个命题（Proposition）。

定义2：设H为识别框架，如果集函数m:2H→[0,1]满足：则称m为识别框架H上的基本可信度分配（Basic Probability Assignment），也称 mass函数。如果 m(A)＞0，A称为焦元（Focal Element），所有焦元的集合称为mass函数的核（Core）。

定义3：设命题A⊆H，则信度函数Bel:2H→[0,1]定似真函数Pl：2H→[0,1]定义为显然

Pl(A)≥Bel(A)，信度函数和似真函数分别为命题A的上下限。

1.2.2 Dempster合成法则

Dempster证据合成法则是一个反映证据的联合作用的法则。如果已知在同一识别框架上几个相互独立的证据的信度函数，且它们不是完全冲突的，那么就可以利用Dempster证据融合规则得到这几个证据的联合信度函数，该信度函数称为这几个证据信度函数的直和。Dempster证据合成法则如定理1所述。

定理1：设m1,m2,…,mn是统一识别框架上的基本可信度分配，Bel1,Bel2,…,Beln是与之对应的信度函数，如果这n个信度函数的组合Bel1⊕Bel2⊕…⊕Beln存在且基本可信度分配为m，则：

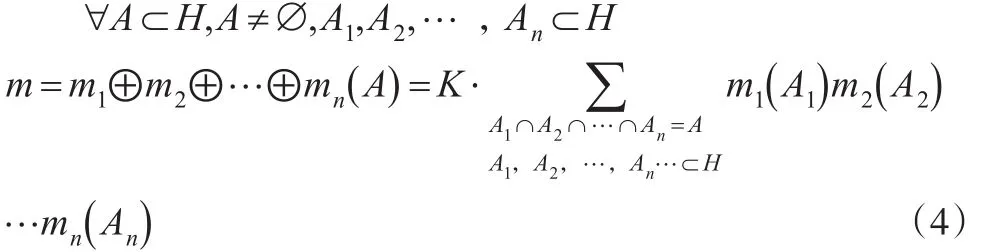
其中k为冲突因子，表达式为：

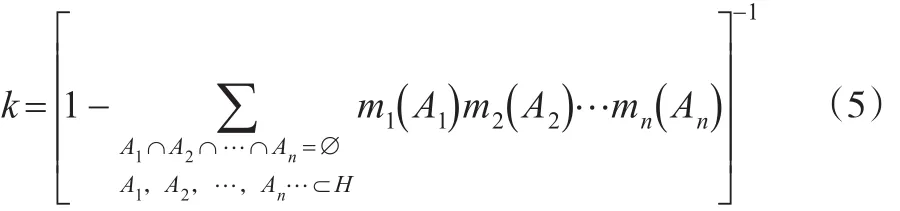
Dempster证据合成法则也称作D-S证据合成法则，它满足交换律和结合律。合成结果反映同一识别框架上几个不同证据对命题A的联合支持程度。

1.3 D数理论

证据理论的识别框架和基本概率分配都基于强烈的假设条件，这严重制约了证据理论表达各种不确定信息的能力。

第一，证据理论的识别框架必须要求是互不相容的基本命题（假设）组成的完备集合。但是，在多数情况在这些假设是难以被满足的。例如，在语言评价中，经常会用到“非常好”，“好”，“一般”，“不好”，“很不好”等语言评价等级。但是这些语言评价等级之间包含交叉部分，因此在这种情况下证据理论的识别框架很难保证完全独立。

第二，基本概率分配必须满足完整性约束，即基本概率分配中焦元的和等于1。但是，多数情况下，决策者并不具备所有知识，因此只能基于部分信息进行评估，从而获得不完全的基本概率分配。在开放世界，不完全的识别框架可能导致不完全的信息表达。证据理论不能融合含有不完全基本概率分配。此外，证据理论融合规则的计算量大，过于复杂，一定程度上限制了它的应用。

为了克服证据理论的上述缺陷，邓勇[6]提出了一种新的表达不确定信息的理论D数。

定义4：设Ω为有限非空集合，如果集函数D:Ω→[0,1]满足：

其中，∅表示空集，B表示Ω中的一个子集。

可以看出D数的定义类似于mass函数，但是不同之处在于，第一，不同于证据理论的识别框架，在D数中Ω所包含的元素并不要求相互独立。第二，在D数中完整性约束不在被要求。如果，则称信息完全，如果，则称信息不完全。

例1：假设评估一个项目，评估得分用区间[0，100]表示，根据证据理论，专家可以给出BPA表达评估结果：

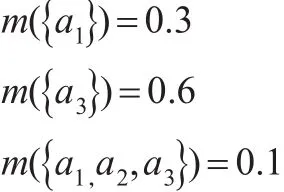
其中，a1=[0,40],a2=[41,70],a3=[71,100]。{a1,a2,a3}构成识别框架。

然而，另一个专家根据D数表达评估结果：

其中b1=[0,45],b2=[38,73],b3=[61,100]。实际上，这里{b1,b2,b3}不是识别框架，因为{b1,b2,b3}中的元素并不满足相互排斥。由于D({b1})+D({b3})+D({b1，b2,b3})=0.9 ，因此信息是不完全的。本例表明了mass函数与D数之间的区别。

对于一个离散集合 Ω={b1,b2,…,bi,…bn} ，其中bi∈R，并且bi≠bj,i≠j，D数的特殊形式可以表示为：

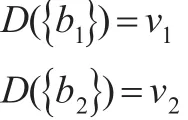
或 者 简 化 表 示 成D{(b1,ν1) ，(b2,ν2),…，(bi,νi),…，(bn,νn)})，其中νi＞0，且定义5：置换不变性存在两个D数满足：则D1⇔D2。

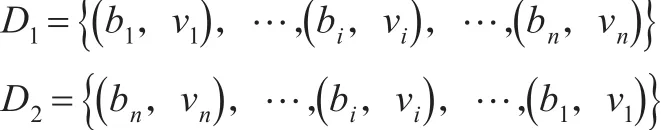
例2：存在两个D数：D1={( 0 ,0.7)，(1 , 0.3) }，且D2={(1 ,0.3)，(0 ,0.7) }，则D1⇔D2。

定义6：对于D={(b1,ν1) ，(b2,ν2),…，(bi,νi),…，(bn,νn)}，其D数集结表达式为：

其中bi∈R，νi＞0，且

例3：D={(1 ， 0.2) ，(2 ，0.1) ，(3 ，0.3) ，(4 ，0.3) ，(5 ，0.1)}，则I(D)=1×0.2+2×0.1+3×0.3+4×0.3+5×0.1=3.0

1.4 基于D-DEA交叉效率的评价方法

考虑到D数能很好地客服决策者的主观性以及融合模糊属性，本文运用D数理论来集结交叉效率值，其过程如下：

第一步：计算评价指标体系中定量指标的交叉效率值，交叉效率矩阵中每行的效率值利用每个决策单元的最优权重分别计算得到。

第二步:对评价指标体系中定量指标的交叉效率值和定性指标分别进行模糊等级转换，得到转换后的评价指标信息矩阵。模糊等级转换方法具体如下:

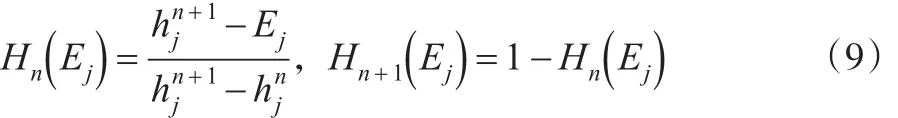
其中，Hn(Ej)和Hn+1(Ej)分别表示定量指标隶属于等级Hn和Hn+1的隶属度。

（2）对于定性指标，建立评价等级，将评价指标体系中定性值与等级进行对应转换。例如定性指标采用5个评价等级，即H=（{很差）H1，（差）H2，（一般）H3，（好）H4，（很好）H5)。其中,H1对应于1,H2对应于2,H3对应于3,H4对应于2,H5对应于5。

第三步:运用式（8），按照评价指标体系由下向上依次进行集结，逐层计算不同指标的（ID），并根据I（D）值的大小进行排序。

2 算例分析

为便于说明本文方法的可行性和优越性，运用文献[4]、文献[11]和文献[12]中的算例数据进行说明。下面对8个实验室进行评价，其中评价指标体系分为人力财力和综合管理2个一级指标，人力财力包括3个定量的二级指标，人数、资金投入2个输入指标和社会委托检验1个输出指标，而综合管理包括3个定性的二级指标运行管理、实验科研和资源共享。各指标评价值和权重已知（见表1）。根据上述评价方法对8个实验室I1，I2，…I8进行评价。

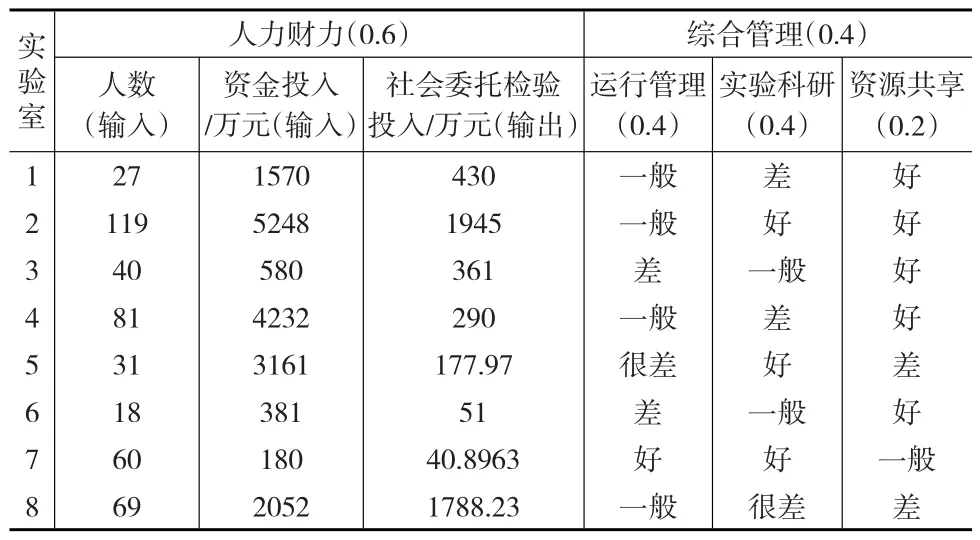
表1 评价指标体系

（1）本文采用压它型策略的交叉效率评价模型[5],利用Excel软计算得到人力财力指标的DEA交叉效率矩阵，如表2所示。

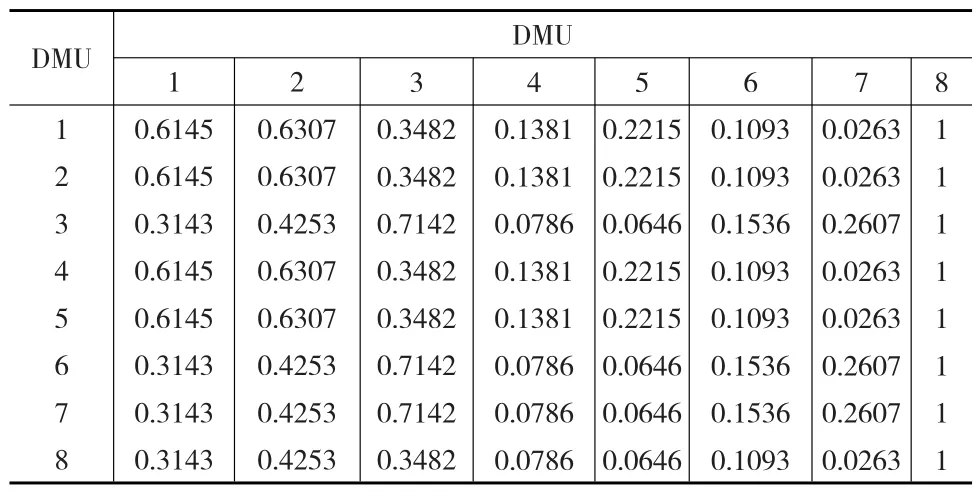
表2 DEA交叉效率值

（2）假设评价等级为5级，即（1，2，3，4，5）≜（很差，差，一般，好，很好），等级效用分别为（0，0.25，0.5，0.75，1）。假设人力财力指标交叉效率值对应的不同等级定性值为（0，0.25，0.5，0.75，1）。

（3）运用式（9）将表2中每个决策单元的交叉效率值进行模糊等级转换，得到转换后的评价指标D数矩阵。然后运用式（8）对其进行集结，在集结过程中仍采用文献[12]的思路，即实验室自身评价权重为0.8，其他实验室评价权重均为0.0285。计算得到的D数矩阵和I（D）。表略。

（4）将评价指标体系中定性值与等级进行对应转换，得到转换后的评价矩阵（见表3）。

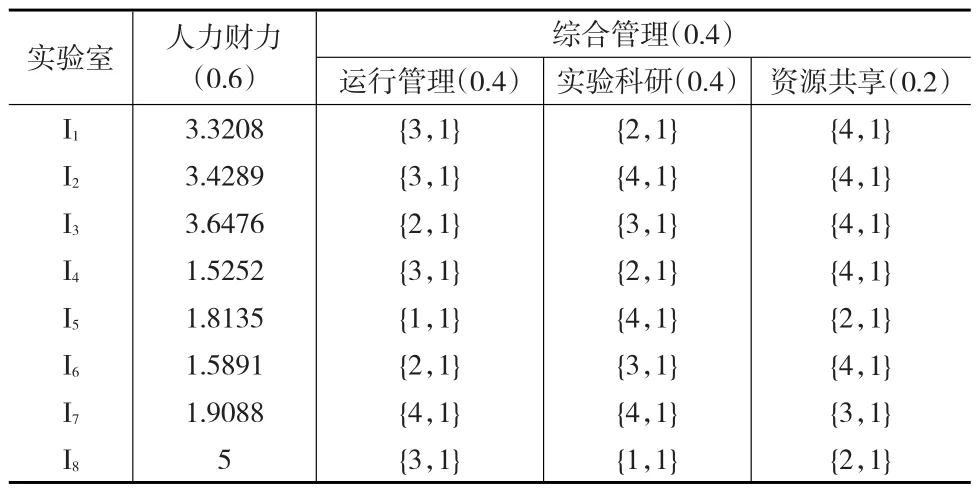
表3 基于模糊等级转化后的评价矩阵

（5）运用式（8），按照评价指标体系由下向上依次进行集结，分别得到8个实验室的I（D），即得到实验室的优劣顺序为I4≻ I2≻ I3≻ I8≻ I7≻ I6≻ I5≻ I1，见表4、表5。

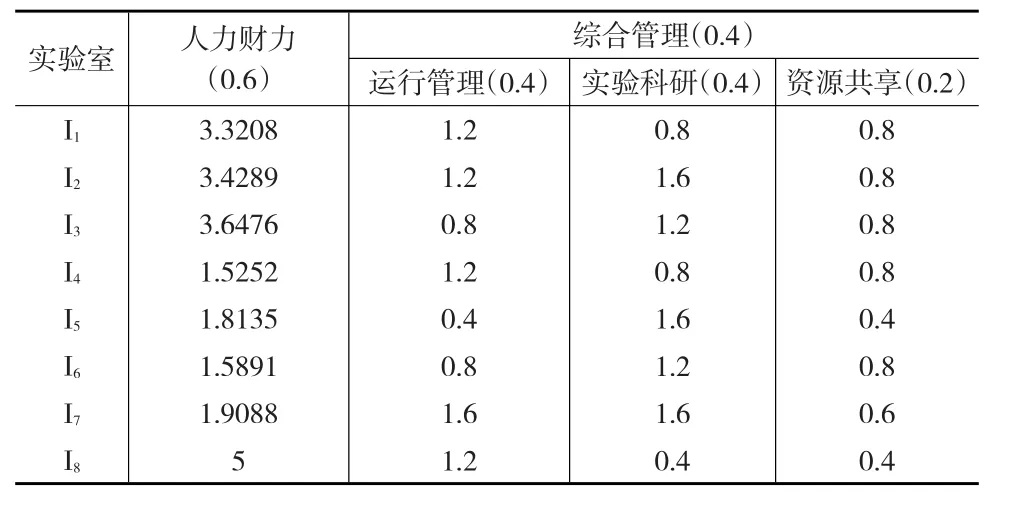
表4 基于D数理论集结交叉效率计算结果

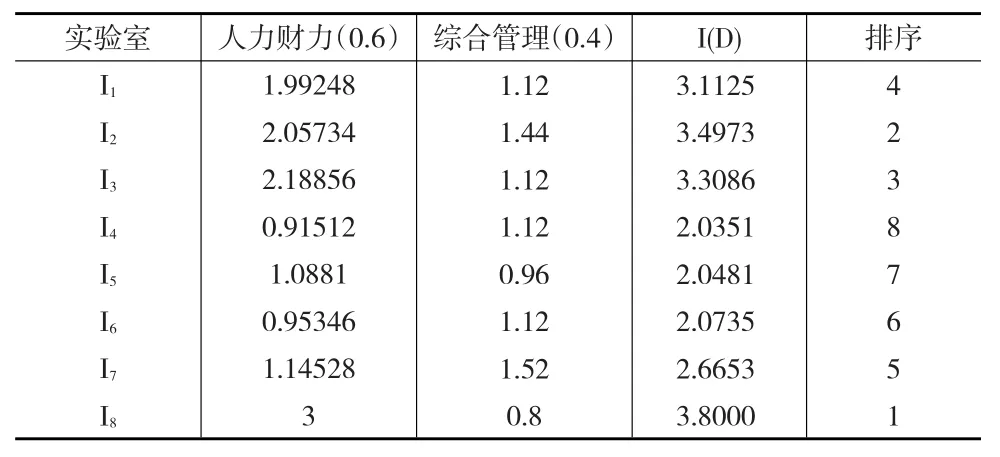
表5 基于D数理论集结交叉效率计算结果及排序

与文献[11]、文献[12]和文献[4]方法进行对比分析，分析结果如下：

与文献[11]方法相比，评价结果基本一致，但本文方法区分度更高（见表6）。

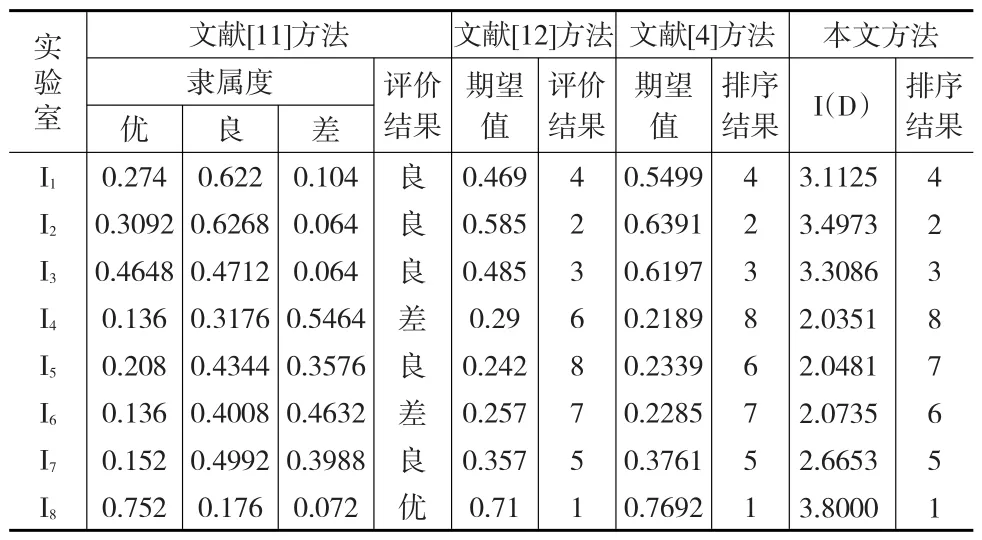
表6 文献[11]、文献[12]和文献[4]方法与本文方法的评价结果比较

与文献[12]方法相比，本文排序结果只在实验室I4，I5和 I6上有所不同，文献[12]中实验室I4，I5，I6的优劣顺序为I4≻ I6≻ I5，而本文中实验室I4，I5，I6的优劣顺序为I6≻ I5≻ I4，从原始数据上看对比实验室I4和I6，在综合管理指标上提供的是相同的信息，而在人力财力指标上通过D数集结计算得到实验室I6的I（D）大于实验室I4的I（D），说明实验室I6优于实验室I4，此结论与文献[4]是一致的。

与文献[4]方法比较，本文排序结果只在实验室I5和I6上有所不同，对比实验室I5和I6的原始数据，在综合管理指标上I5明显弱于I6，而在人力财力指标上通过D数集结计算得到实验室I5的I（D）略大于实验室I6的I（D），从综合的I（D）看实验室I6优于实验室I5。这与文献[12]的结论一致。

3 结论

本文将D数理论与DEA交叉评价效率相结合，提出了一种新的混合型多属性决策方法。该方法通过将定量指标和定性指标进行模糊等级转换，采用D数理论对评价指标信息进行集结，从而克服了现有研究成果中存在的缺陷。最后通过与文献[11]、文献[12]和文献[4]比较分析看出，本文方法是可行的且得出的优劣顺序更为合理，而且计算过程更为简便，为含有投入产出指标的混合型多属性决策问题提供了新的视角。