基于刚-柔耦合模型的供弹系统动力学分析

李 利，魏立新，樊永锋

(郑州机电工程研究所，河南 郑州 450052)

0 引 言

为了提高某型小口径舰炮射击过程中供弹的可靠性，有必要对其供弹系统进行动力学分析。该小口径舰炮的供弹系统属于刚柔耦合系统，尤其是供弹系统弹鼓模块中的双线螺旋片，属于薄板类易变形的柔性体。由于供弹系统模型刚柔耦合效应的存在，会对供弹系统的动力学特性造成很大的影响。目前国内对小口径舰炮供弹系统的研究只限于结构和运动原理上的分析，对其动力学分析的研究较少，特别是对供弹系统进行深一步的刚柔耦合动力学分析。因此有必要建立供弹系统虚拟样机，对供弹系统模型进行刚柔耦合动力学仿真[1]。

供弹系统的主要构件双线螺旋片在高转速、受力大的工况下会产生变形，因此在仿真中必须视为柔性体。其余受力小，刚度大的构件可以视为刚体，这样建立的动力学模型不仅可以准确的反映供弹系统的运动状态，又可以使仿真的工作量大大降低[2]。

文中分别建立了供弹系统的刚柔耦合动力学模型和刚体动力学模型，利用动力学仿真软件Adams分别进行动力学仿真，并与试验结果进行对比，为以后的样机研制提供依据[3]。

1 刚柔耦合模型的建立

1.1 供弹机构的工作原理

供弹系统主要包括弹鼓和供弹机构两大组件，具体模型如图1所示。弹鼓主要用来储存炮弹，为炮弹进入供弹机构提供集弹空间；供弹机构利用自动机火药燃气的后坐力作为动力，通过四级拨弹轮把弹从集弹圆盘的集弹器中带出。在这个过程中，弹鼓中的螺旋片属于易变形构件，刚度小；而炮弹沿隔室移动主要靠螺旋片的推力作用，因此螺旋片的变形很大程度影响供弹机构供弹的可靠性。所以有必要对螺旋片柔性化并对供弹系统进行动力学分析。

1.2 Adams仿真模型建立

Adams动力学分析软件通过建立零件模型、施加载荷和约束建立仿真模型并进行动力学求解。同时Adams支持很多常用CAD设计软件模型的直接导入，但是导入的模型默认为刚体模型，必须使用Adams/Flex模块，通过Flex与FEA软件之间的通信接口，诸如Nastran，Ansys，Abaus建立柔性体的模态中性文件（medal neutral file，MNF）向 Flex 传递模型数据[4]。FEA软件生成的MNF文件中包含的信息主要有：柔性体的几何参数，柔性体各节点的位置坐标，节点的质量与转动惯量，各阶模态以及模态的广义质量和广义刚度等。文中提出一种利用Creo，Adams，Ansys建立刚柔耦合动力学模型的方法[5-6]。

首先在Creo下建立三维刚体模型，由于模型中存在特征较为复杂的零件，因此不采用转换中间格式的方法。直接用Adams导入Creo文件的方法，这样可以更好的保留模型的特征。其次利用有限元分析软件Ansys创建有限元模型，通过划分网格和建立刚性区域及刚性连接点的方式生成mnf中性文件[7]，如图2和图3所示。最后将mnf文件导入Adams中替换刚性体螺旋片，由Adams进行动力学仿真得到仿真结果。

这种分析方法把刚度大、变形小的构件作为刚性体处理，把刚度小，变形大的构件作为柔性体处理。在保证仿真正确性的基础上可以有效的提高仿真效率和逼真度。

1.3 仿真模型的约束和参数设定

将模型导入Adams后，需要建立各个构件之间的约束。因此需要根据模型实际约束情况，在构件间添加约束[8]。文中的仿真主要是计算供弹系统在启动—稳定运转过程中供弹系统的阻力矩，并得到刚体模型和刚柔耦合模型的仿真结果。

动力学仿真中供弹系统的驱动来自于自动机对大模数齿轮的驱动。因此在模型仿真过程中，直接在大模数齿轮上添加角速度驱动，角速度的具体数值和现场试验过程中电机给自动机的角速度一致，是通过Adams中的Akispl插值函数实现[9]。

2 仿真计算与结果

2.1 试验仿真

本文通过对供弹系统启动、稳定射击到停止射击3个阶段分别进行多刚体动力学仿真和刚柔耦合动力学仿真，仿真结果与实际试验结果进行对比，找到更符合实际的供弹系统动力学仿真方法，进而达到利用动力学仿真模拟现场试验、缩短产品研发周期，降低试验成本的目的[10]。

2.2 仿真测量结果

仿真试验主要对供弹系统（刚柔耦合模型和刚体模型）的阻力矩进行仿真。对比刚柔耦合模型和刚体模型的仿真阻力矩，与现场试验进行比较，找出同一供弹系统利用不同类型的仿真模型得到仿真结果的差异[11]。文中按照现场试验的转速进行仿真，仿真过程中，启动时间为330 ms（对应的现场试验时间为500–830 ms）。为缩短仿真时间，提高仿真效率，供弹系统稳定运转时间为270 ms（对应的现场试验时间为830–1 900 ms），减速阶段时间为 400 ms（对应的现场试验时间为 1 900–2 300 ms）。现场试验中射频为4 200发/min，该型舰炮为6管，射速为4 200/6=700 r/min，转换为角速度为：（700/60）*360=4 200 d/s，图4-图5中角速度单位d/s，扭矩单位N·mm。由Akispl函数差值获得角速度变化曲线如图4所示。

表1 仿真试验的初始条件Tab.1 Initial conditions for simulation experiments

刚体模型仿真阻力矩与时间之间的变化曲线如图5所示。

刚柔耦合仿真模型启动力矩与时间之间的变化曲线如图6所示。

3 现场试验结果

3.1 现场试验测试原理

在不进行真实射击情况下，扭矩传感器安装在电机的输出轴和自动机传动轴之间。扭矩传感器采用TQ-660系列扭矩传感器，测量范围为±500 N·m，响应频率为100 μs，精度为0.5%，扭矩传感器的具体位置如图7所示。

在现场试验中，由于扭矩传感器的安装位置在自动机尾部，所以扭矩传感器测出的力矩为自动机产生的阻力矩与供弹系统阻力矩之和。在对比过程中，应该减去自动机产生的阻力矩。由于自动机做了相应的简化，其阻力矩为 2 N·m。

3.2 现场试验

在试验中，电机按照已经设置好的转速驱动自动机进行运动，自动机驱动供弹机构的四级拨弹轮产生运动。四级拨弹轮通过齿轮将动力传入弹鼓，使螺旋片产生旋转运动，炮弹从弹鼓中的隔室经螺旋片的推力作用上移至供弹圆盘，供弹圆盘中的炮弹经四级拨弹轮的作用进入自动机，随后在不进行真实射击的情况下经过自动机依次进入排壳机构。

3.3 现场试验结果

现场试验采用射频为4 200发/min进行带弹射击试验。速度单位为r/min（等同仿真过程中的射频4 200 d/s），扭矩单位为N·m。

由现场试验得到角速度曲线，启动力矩的变化曲线如图8和图9所示。

如图9可知，供弹系统在刚开始启动时阻力矩很大，最大值达到113 N·m（此处减去了自动机的阻力矩2 N·m）。但是随着供弹系统转速的稳定，其阻力矩开始逐渐减小，稳定在23 N·m（此处减去了自动机的阻力矩2 N·m）附近。在供弹系统开始减速至停止阶段，发现得到的扭矩曲线与仿真试验测得的图像差别很大。这是由于现场试验是电机轴驱动整套试验系统运转，传感器测得的扭矩是电机输出轴上的扭矩。当电机突然断电停转后，电机轴在其惯性作用下继续做减速运动。但减速的过程中电机的输出轴是靠惯性继续运动，其轴上是不存在力的，因此也不会存在扭矩。

4 仿真结果对比

4.1 结果对比

文中从供弹系统启动和供弹系统稳定运转2个阶段对阻力矩进行仿真分析，得到结果如表2所示。

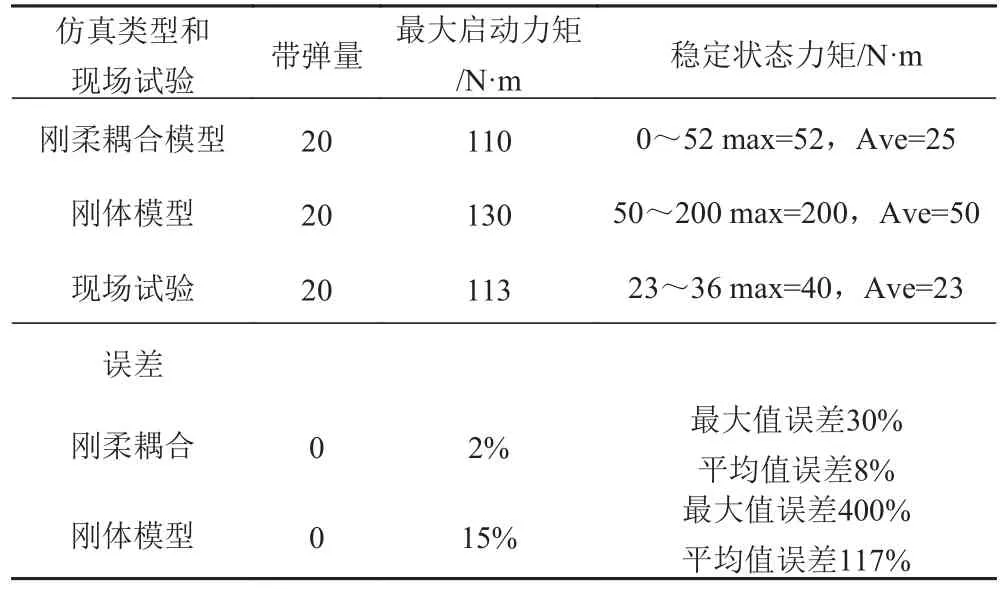
表2 仿真结果与试验结果对比Tab.2 Comparison of simulation results with test results

4.2 仿真试验结论

从表2的分析可以看出，现场试验测得的扭矩随角速度变化曲线和刚柔耦合仿真模型的扭矩随角速度变化曲线最为接近。

分析启动力矩，首先从图7看出扭矩传感器安装的位置在自动机的尾部，也就是说现场试验测得的扭矩是供弹系统的阻力矩外加自动机的阻力矩。分析刚体仿真模型在启动阶段的阻力矩可以看出，虽然趋势和现场试验一致，但是其最大启动力矩要大于现场试验的最大启动力矩。而刚柔耦合模型不仅趋势与现场试验一致，而且最大启动力矩与现场试验的最大启动力矩误差很小。对比刚柔耦合模型的最大启动力矩和刚体模型最大启动力矩可以看出，刚柔耦合模型的最大启动力矩要小于刚体模型的最大启动力矩，这是符合刚体动力学的一般常识的，进一步验证了刚柔耦合仿真模型的正确性。从图5可以看出，刚体仿真模型在启动到接近稳定射击状态的过程中，其阻力矩出现了较大的波动，可以从另一方面说明刚体仿真模型的不稳定性。

本文对刚体模型和刚柔耦合模型稳定射击状态下供弹系统的最大阻力矩与实验结果进行比较。刚体模型射击稳定状态时的最大阻力矩为200 N·m，这与现场试验测得数据40 N·m相差很大，不能够模拟现场试验。而刚柔耦合模型射击稳定状态的最大阻力矩为52 N·m，这与现场试验时稳定射击状态的最大阻力矩较为接近。

停射力矩可以看出是最偏离现场试验数据的，具体原因上文已经阐述。通过刚柔耦合模型与刚体模型之间的对比，得到刚柔耦合模型的阻力矩比刚体模型阻力矩要小，符合刚体动力学常识，可以验证刚柔耦合模型的正确性。

所以可以得出结论，刚柔耦合仿真模型较比于刚体仿真模型而言，得到的结果更符合现场试验，因此在供弹系统动力学试验中可以采用刚柔耦合模型来指导现场试验，获取想要的结果。

5 柔性体螺旋片变形仿真

对于柔性体而言，主要考虑其在仿真过程中的变形量。利用这个参数来进一步验证供弹系统的可靠性以及刚柔耦合模型的正确性。

螺旋片任意点处的变形如图10所示。

由以上仿真实验可以获得螺旋片在各个阶段的变形如表3所示。

表3 柔性体变形量Tab.3 Flexible body deformation

由表3可知，螺旋片在供弹系统刚开始启动时变形量逐渐增加，最大值为0.000 2 m；当供弹系统稳定运转时，螺旋片继续变形，变形量稳定在0.000 2～0.000 3 m之间；当供弹系统停射时，此时螺旋片会产生整个供弹阶段最大的变形量为0.000 5 m。从以上的分析可以看出螺旋片在整个运动阶段变形量相对于螺旋片的厚度是比较小的（螺旋片的厚度为0.004 m，焊接在弹鼓的内筒上），因此螺旋片的变形量不会影响弹在隔室中的上升运动，即不会影响供弹的稳定性，也从侧面验证了刚柔耦合模型的准确性。

6 结 语

文中采用Creo，Adams，Ansys软件之间的双向接口建立了供弹系统刚柔耦合模型，并在射频为4 200发/min下分别对供弹系统的刚体模型和刚柔耦合模型进行动力学仿真分析，得出在启动阶段，刚柔耦合模型和刚体模型与现场试验中供弹系统的最大阻力矩误差分别为2%和15%；在射击稳定状态下，刚柔耦合模型和刚体模型与现场试验中供弹系统的阻力矩最大值的误差分别为30%和400%。通过对比可以得出相对于刚体动力学模型，刚柔耦合仿真模型更加接近于现场试验，为供弹系统研究提供了一种有效的动力学建模方法和分析手段。