全向停车控制交叉口中行人与机动车延误相互影响研究
2018-12-20温豪杰吴先宇袁振洲
温豪杰,吴先宇, 袁振洲
(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京 100044)
交叉口作为城市道路网上的节点,是城市道路交通系统的咽喉。据统计,有80%的延误发生在交叉口。因此,对交叉口进行延误分析,可以准确地掌握交叉口的通行能力,为进一步评价城市道路以至整个路网的运行质量提供可靠的定量依据。而无信号交叉口作为最普通的交叉口类型之一,虽然其通行能力一般低于信号交叉口,但在路网交通控制中起着非常重要的作用。
针对无信号交叉口的延误,国内外学者已经做了大量的研究工作。在行人过街延误方面,国外较为成熟的研究成果有美国的HCM模型、澳大利亚的Virkler模型等[1],北卡罗莱纳州大学的Rouphail等在成群行人的可穿越间隙的基础上建立了行人延误模型,Ishaque等[3]用VISSIM对人车交互模型进行仿真,通过改变行人和车辆参数来矫正模型。国内的研究如冯树民等[4]针对行人一次穿越一条车道和多条车道出现可穿越间隙下过街两种情况,推算出行人过街平均延误的计算方法;杨晓光等[5]以行人过街延误为依据,建立了无信号控制下行人过街延误计算模型;廖明军等[6]研究了行人交通流的交通特性,讨论了关于行人运动行为的内容以及相应的研究方法;李庆丰等[7]提出了一种新的人行横道行人延误的测量方法;张珩等[8]通过对中国行人过街行为的分析,建立了无信号交叉口行人从众过街对交通流延误的影响模型,反映了行人违章过街对交通流延误造成的巨大影响。
在机动车通行能力和延误方面的理论研究较为丰富。Tanner[9]基于可接受间隙理论,在交叉口主路车流优先的情形下假设主路车流车头时距服从负指数分布,提出了一种计算支路通行能力的方法;随后 Cowan[10]改进了负指数分布,给出当主路车流车头时距服从M3分布时,支路通行能力的计算公式;李淑庆等[11]建立了无信号交叉口处左转车流的通行能力模型;李文燕[12]基于间隙接受理论,对无信号T型交叉口的通行能力进行了建模仿真研究;王殿海等[13]改进了无信号交叉口的可插车间隙理论模型,假设直行车只有部分优先权,提出了两相位交叉口处左转车辆的通行能力计算模型,与传统模型相比该模型误差更小,计算结果更符合实际。
近年来,学者对于信号交叉口的人车冲突交互行为分析研究成果颇丰。曹更立等[14]基于机动车行驶安全性与舒适性,提出了信号交叉口展宽段及渐变段的计算模型;刘艳婷等[15]运用生存分析方法比较了信号交叉口行人与自行车等待忍耐时间的分布以及等待行为影响因素的异同;于瑞康等[16]分析了信号交叉口过街行人堆积与右转机动车之间的冲突行为,得出了行人堆积数量与右转机动车延误之间强相关的结论。然而近期关于无信号控制交叉口人车交互的研究较少,且鲜有创新性的理论分析模型提出。
全向停车控制(all-way stop-controlled,AWSC)作为无信号交叉口的一种常用控制形式,要求交叉口的所有引道都设置停车标志,即所有引道上的驾驶员在进入交叉口前必须停车。驾驶员要根据道路规则(如右侧驾驶员具有优先通行权)和其他引道的交通状况决定是否前进。目前在一些区域的公认规则是给予右侧驾驶员较高的优先权,但事实上规则的确立应当取决于交叉口的几何线形以及车辆到达停车线的模式。
在国内外目前关于AWSC交叉口的研究中,多侧重于机动车的通行能力、延误以及行人延误,而很少关注到行人过街延误与机动车延误之间的相互影响,并没有去探索两者之间的内在联系。本文主要通过对某一典型AWSC交叉口的视频数据进行处理,研究行人过街延误与机动车延误的相互关系,为更加准确地掌握无信号交叉口通行能力、进一步评价整个路网的运行质量提供可靠的依据。
1 研究区域
本文选取美国内华达州里诺市某AWSC交叉口为研究对象,该交叉口由东西向E 9thSt和南北向N Center St相交而成。其中东西向进口道分别只有一条车道,为直左右车道,略有展宽;南北向进口道分别有两条车道,一条直右车道,一条左转专用车道。人行横道长度均为11 m(图1)。
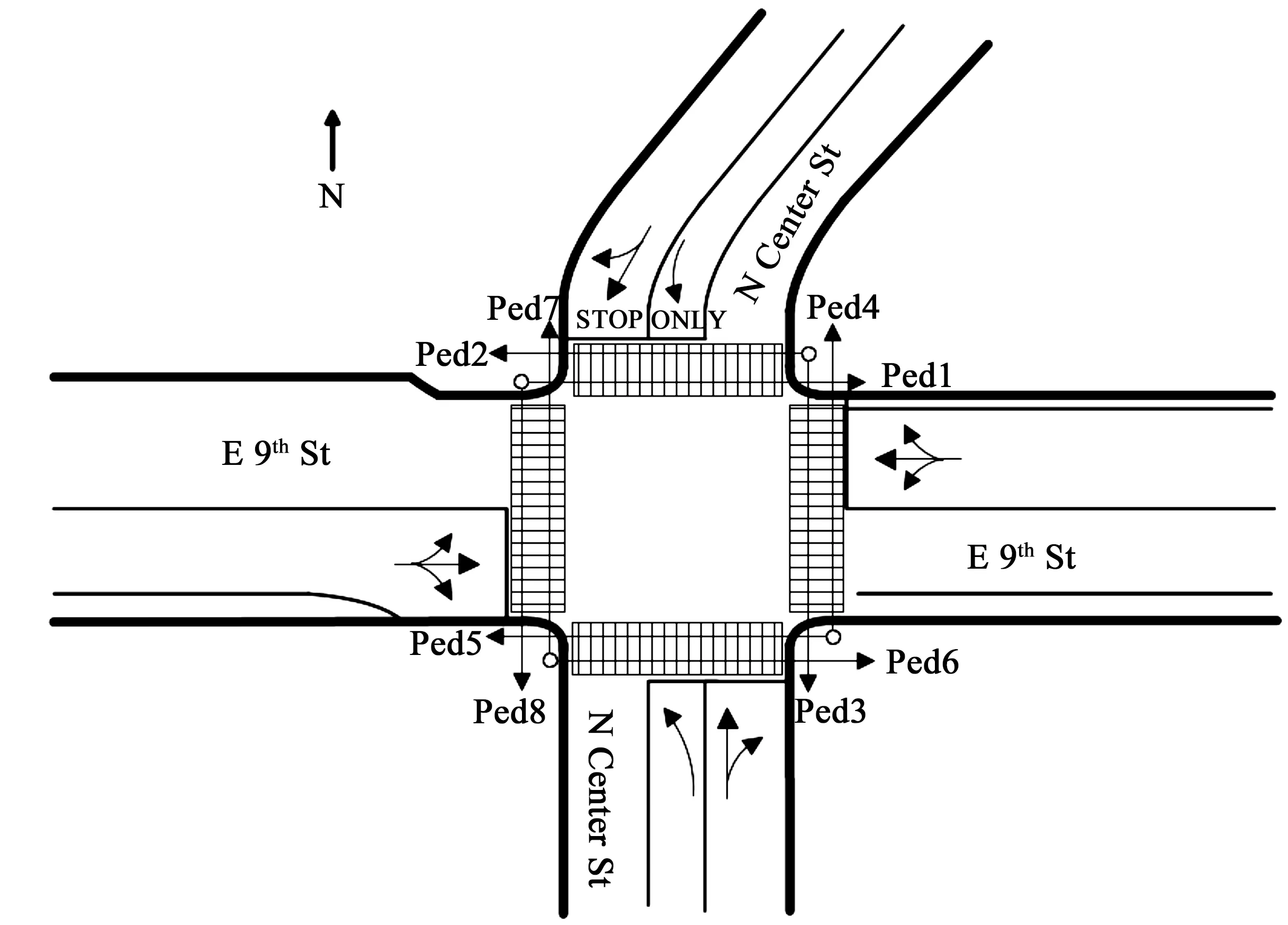
图1 AWSC交叉口示意图Fig.1 Diagram of the AWSC intersection
2 模型研究
2.1 AWSC交叉口冲突分析
鉴于时间和水平有限,本文只针对行人与机动车之间12类最基本冲突情形进行研究,如图2所示,这些情形中,无其他冲突车流存在,且机动车在行人过街之前(或同时)已经在停车线前停车。
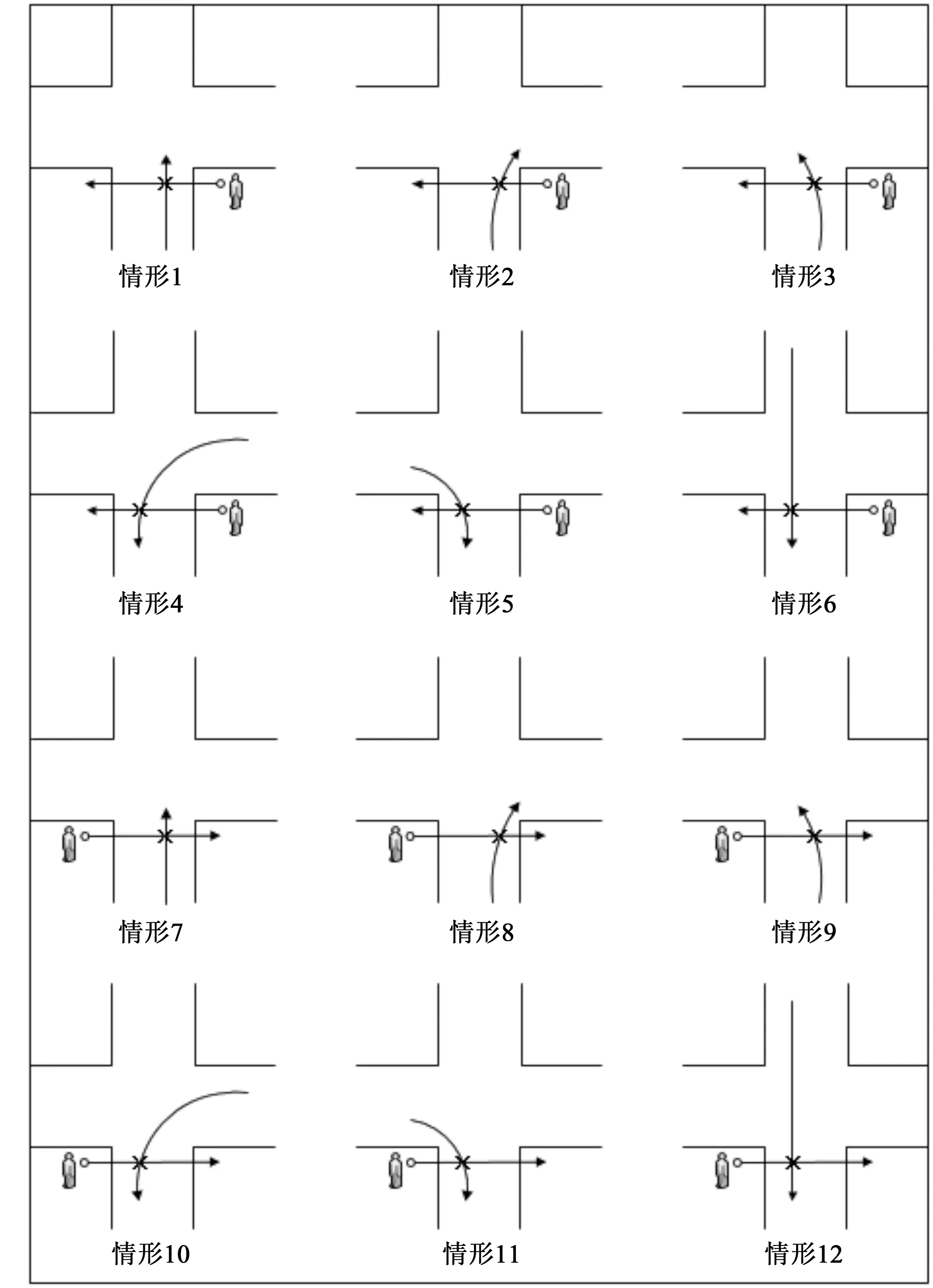
图2 行人与机动车12类基本冲突情形Fig.2 The 12 types of conflicts between pedestrians and vehicles
对该研究区域AWSC交叉口视频(1 h,16:00—17:00)进行数据统计。对于机动车,统计数据包括车辆数、转向、到达交叉口时刻、到达队首时刻以及出发时刻;对于行人,统计数据包括行人数、走向、到达人行横道时刻、出发时刻、完成过街时刻。
结合视频,从原始数据中找出符合以上12类基本冲突的行人-机动车冲突组合,并分别一一对应,形成冲突对。现摘录部分数据如表1所示。
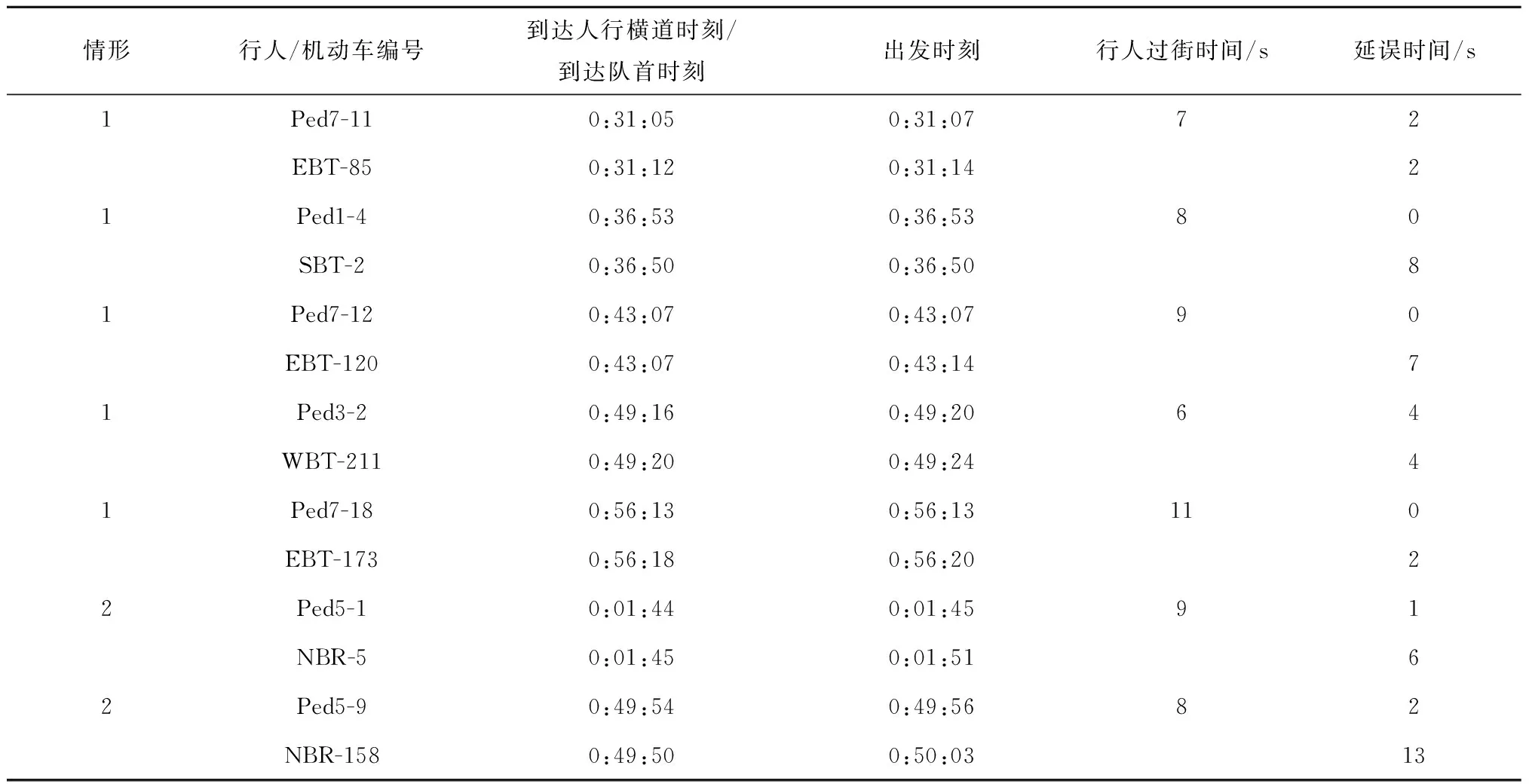
表1 行人-机动车冲突组合
2.2 行人与机动车延误相互关系模型
当行人过街对机动车通过交叉口造成影响时,机动车的延误由原本的停车时间(没有行人时)、行人延误时间和行人过街时间三部分组成[17]。
2.2.1 行人半过街模型
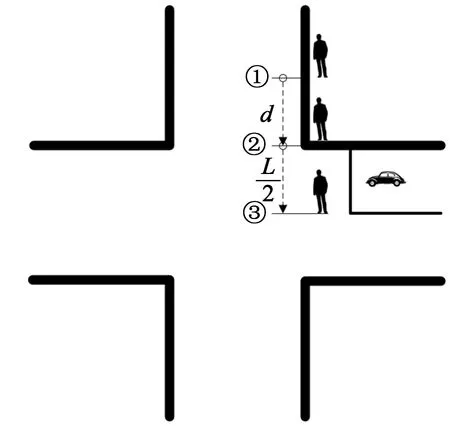
图3 行人半过街情形示意图Fig.3 The situation of pedestrians crossing halfway
在图2中的情形1、2、3、10、11、12中,机动车在行人过街完成一半时即可通行。虽然不符合全向停车控制交叉口过街规则,即要求待行人完全过街后机动车方可通过,但结合当地驾驶人员习惯,这种情形发生较为普遍。与此同时,通过视频观测可以发现,当机动车驾驶员按照AWSC交叉口通行规则停车后,若发现尚未到达人行横道的行人有过街意图,一般会在停车线前继续停车等待,直至行人过街完成一半,即如图3所示,当机动车停车时,行人到达位置①,此时机动车继续等待;当行人到达位置②时,可能会对机动车是否前进做出判断,判断时间即为行人延误;判断完毕后行人开始过街,到达位置③时过街完成一半,此时行人不再对机动车通行造成影响,机动车可以启动。
因此,行人半过街情形下,行人与机动车延误相互关系模型可建立如下:
(1)
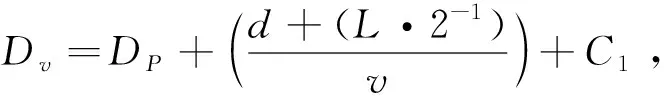
(2)
式中,Dv为机动车延误,s;Dp为行人延误,s;d为行人距离人行横道的距离,m;L为人行横道长度,m;v为行人走行速度,m/s;C1为无行人时机动车的停车时间,s,经计算约为1.8 s。
2.2.2 行人完全过街情形

图4 行人完全过街情形示意图Fig.4 The situation of pedestrians crossing completely
图2中的情形4 ~ 9,机动车必须在行人完全过街后才能通行,即如图4所示,当机动车停车时,行人到达位置①,此时机动车继续等待;当行人到达位置②时,可能会对机动车是否前进做出判断,判断时间即为行人延误;判断完毕后行人开始过街,到达位置③时过街全部完成,此时行人不再对机动车通行造成影响,机动车可以启动。
因此,与行人半过街情形同理可得行人完全过街情形下,行人与机动车延误相互关系模型可建立如下:
(3)
其中,C2为无行人时机动车的停车时间,C2=C1,约为1.8 s。
2.3 行人与机动车延误相互关系模型评价
本文采用实地交叉口数据以及交通软件仿真获取的仿真数据,进行对模型的验证评价。
2.3.1 实地调研数据验证
(1)半过街情形
将模型计算出的延误与视频统计的实际延误对比,对模型进行验证,见表2。
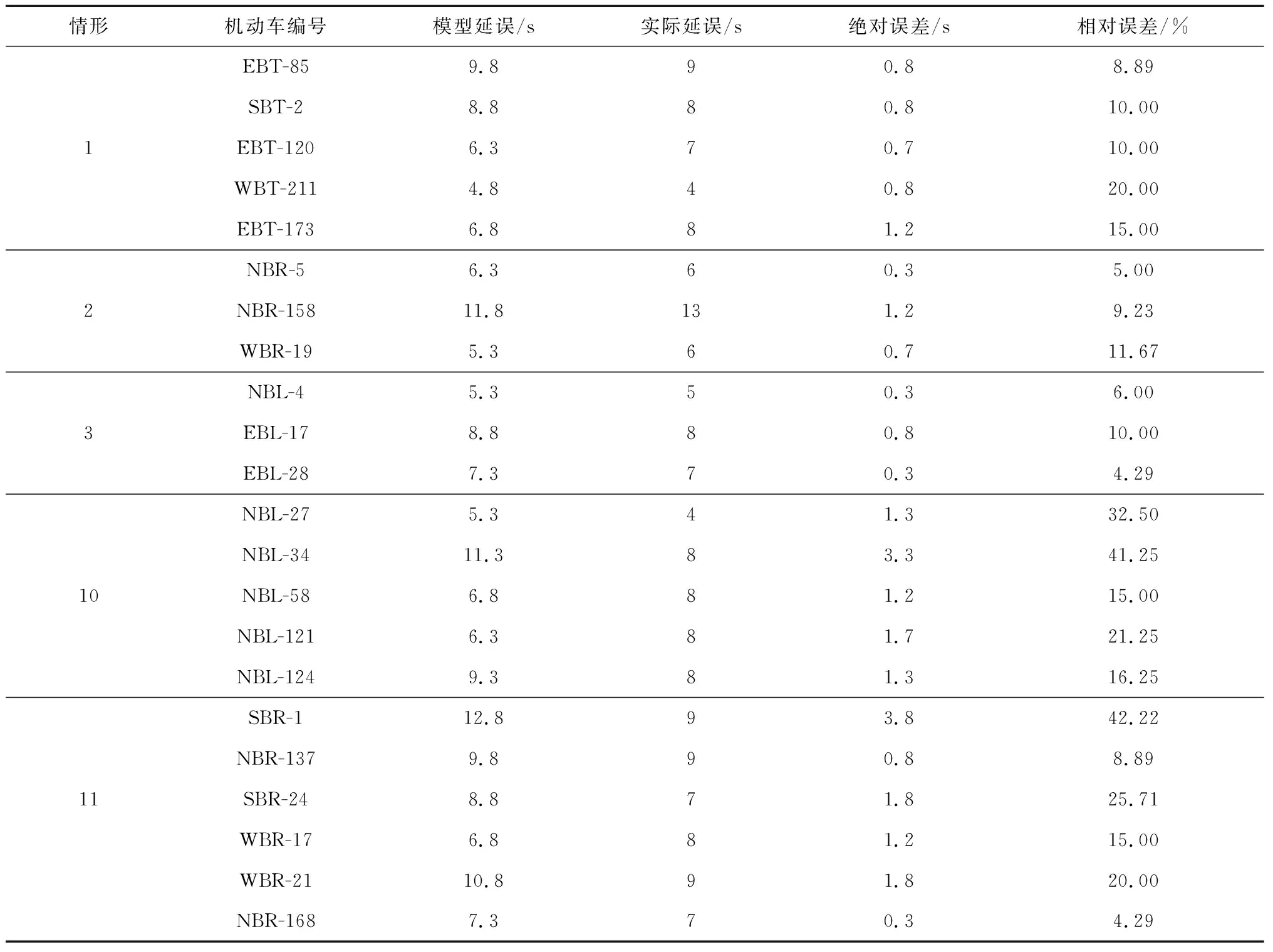
表2 半过街情形模型延误与实际延误对比Table 2 Comparison of delay between the halfway crossing model and actual situation
续表2
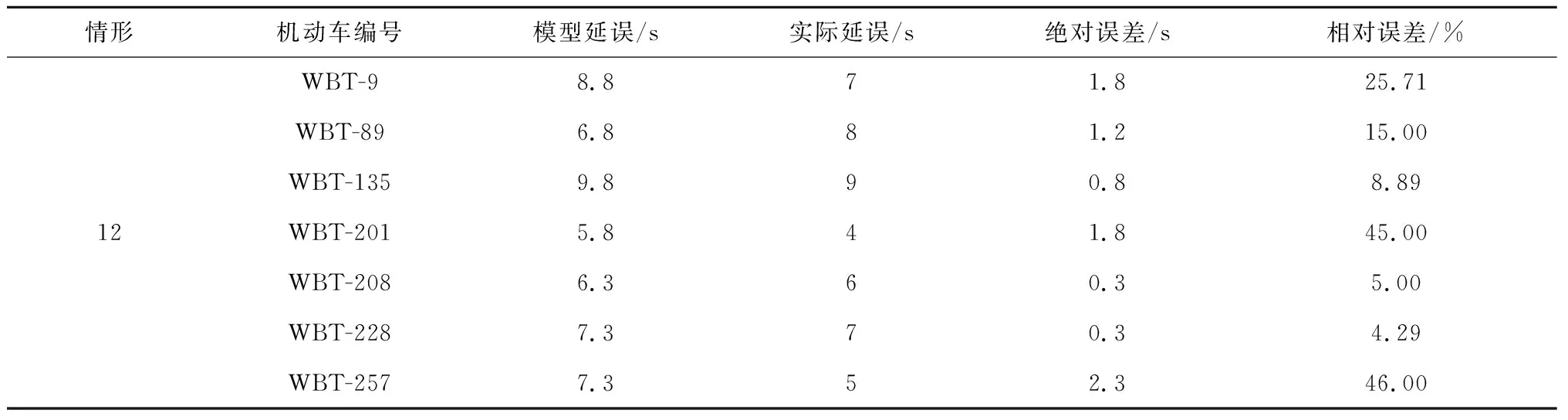
情形机动车编号模型延误/s实际延误/s绝对误差/s相对误差/%WBT-98.871.825.71WBT-896.881.215.00WBT-1359.890.88.8912WBT-2015.841.845.00WBT-2086.360.35.00WBT-2287.370.34.29WBT-2577.352.346.00
从表2可知,有21组数据的相对误差≤20%,有8组数据的相对误差>20%。按照相对误差低于20%为拟合标准,行人半过街模型情形的29组数据中有21组数据符合标准,符合率为72.4%。
模型对过街情形1、2、3拟合情况较好,并没有出现误差大于20%的情形,误差较大的情况均出现于过街情形为10、11、12的场景。对比情形1、2、3与情形10、11、12,发现前者场景的人车交互距离较近,可见在近距离情况下,机动车与行人延误接近理论模型的预测值。而当人车交互距离较远时,位置不确定性的增加使得驾驶员与行人之间心理博弈造成的随机性增加,因此这部分数据中有部分样本误差较大,无法较好拟合模型。同时,部分机动车在可以实现半过街的情形中依旧选择等待行人完成过街后再前进,这种在半过街情形中机动车启动时间的不确定性也大大增加了误差,这部分误差是当前模型无法去拟合的。
(2)完全过街情形
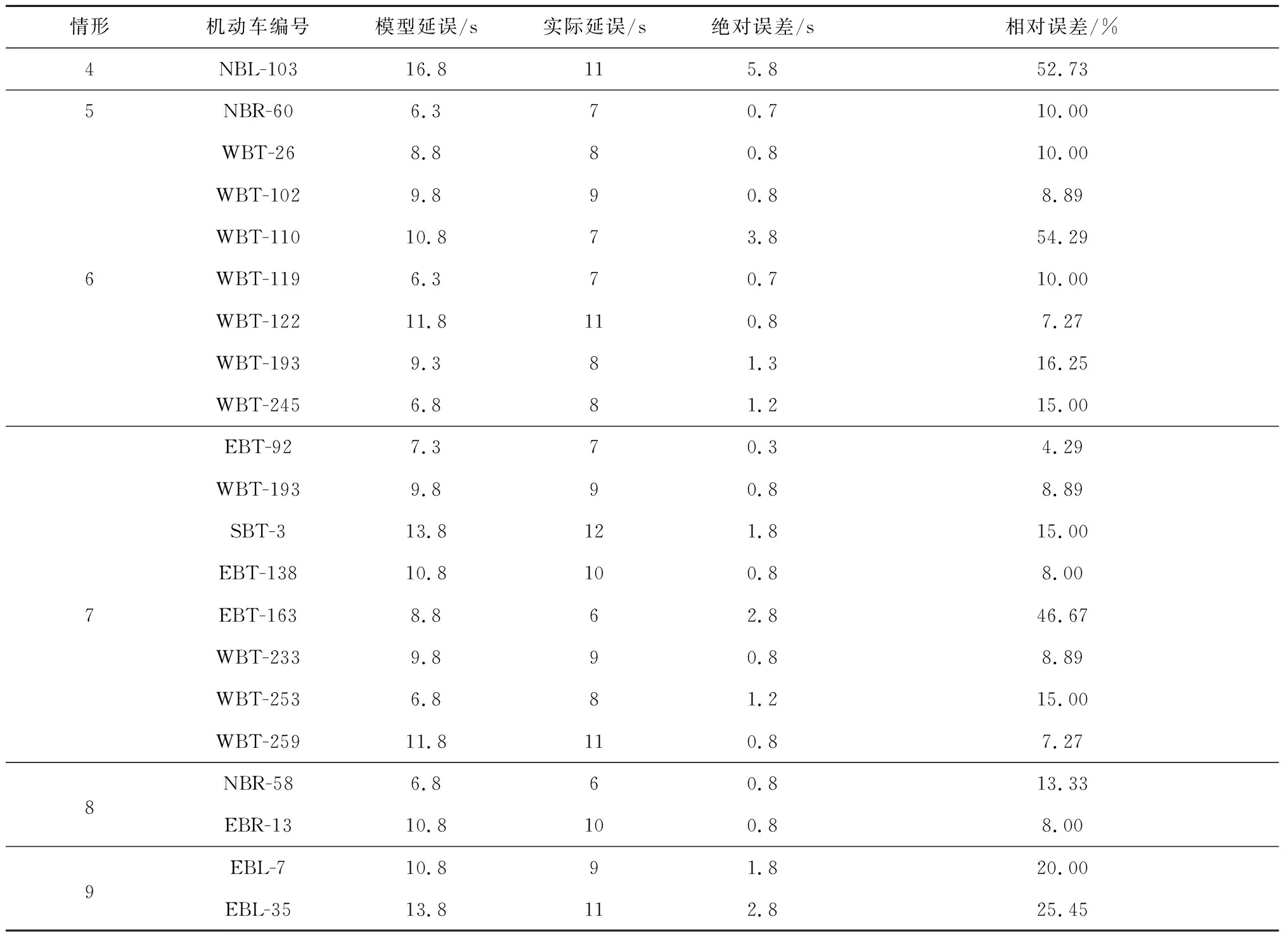
表3 完全过街情形模型延误与实际延误对比Table 3 Comparison of delay between the crossing completely model and actual situation
从表3可知,有17组数据的相对误差≤20%,有4组数据的相对误差>20%。行人完全过街情形的21组数据中有17组数据符合标准,符合率为81.0%。
模型可以拟合的样本数量超过80%,拟合效果较好。误差较大的4组数据在情形4、6、7、9中各有一例。通过对视频研究发现,由于这几种情形下行人和机动车交互距离较远,而且根据观察,有部分机动车未遵守AWSC规则,在行人过街前通过交叉口,使部分样本真实延误与模型计算结果存在一定误差。
(3)模型验证结论
从验证结果总体来看,建立的理论模型从很大程度上解释了AWSC交叉口机动车与行人延误之间的关系,拟合效果较好。人半过街和完全过街情形下的行人与机动车延误相互关系模型由于时间和水平有限,还存在一定的误差,有待完善,但同时也为进一步的研究提供了新思路。
2.3.2 仿真验证
Synchro是一款由美国Trafficware公司根据美国交通部标准HCM研发的一款交通配时优化软件,同时具备通行能力仿真功能,其仿真特性较为符合美国出行习惯。本文利用Synchro软件对行人与机动车延误相互关系模型进行评价,通过建立交叉口、车道和流量等参数设置,在完成设置后输出仿真结果,部分结果如表4所示。
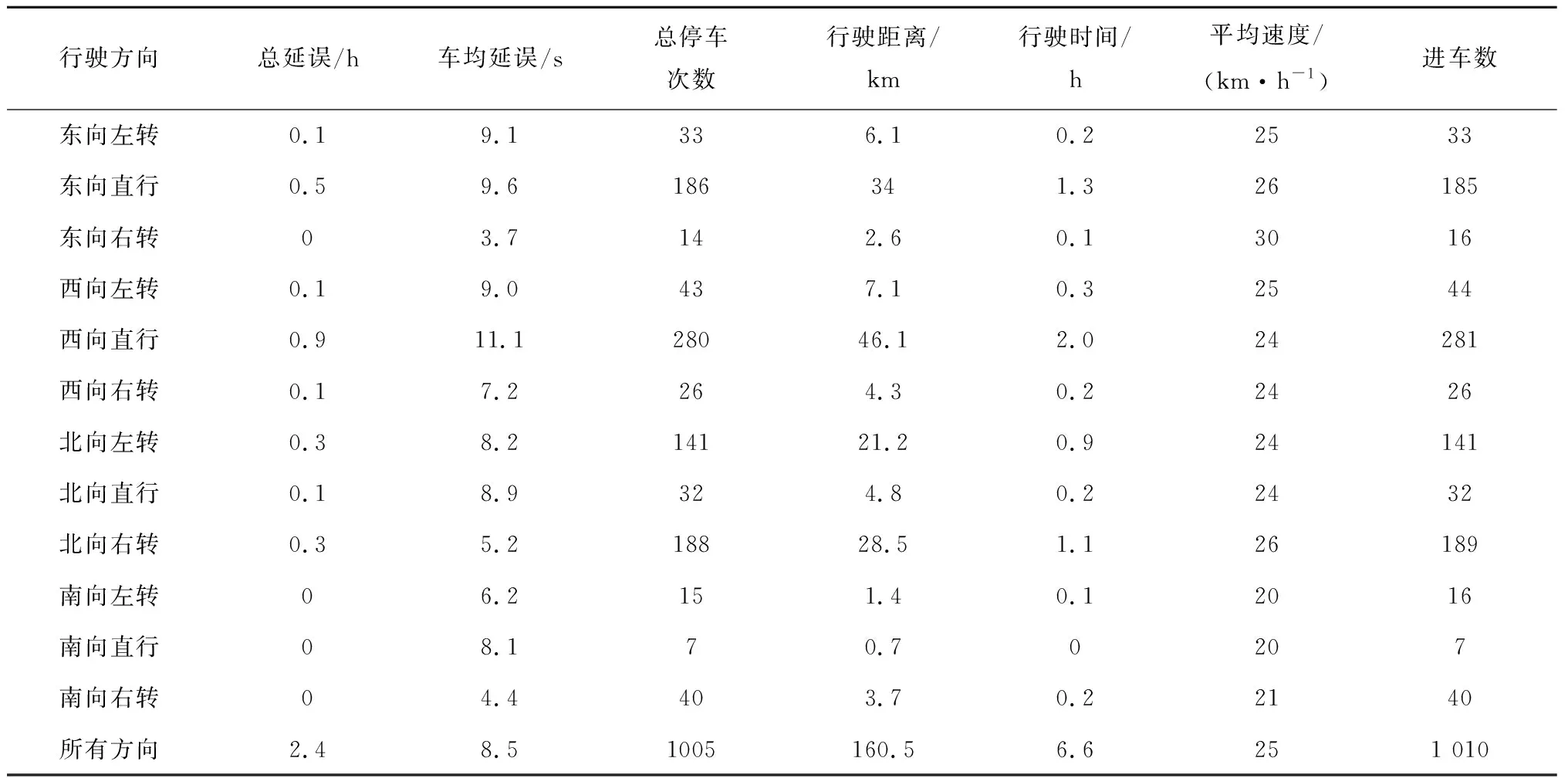
表4 仿真结果
从仿真结果来看,各个进口道的仿真延误和实际延误有很大差异。这是由于Synchro内部并没有针对AWSC交叉口规则制定的仿真过程。
事实上,目前并没有交通软件能对此类交叉口做相应的仿真。因此,目前无法利用现有仿真软件对模型进行准确地评价,只能通过实测数据与模型计算结果对比来验证模型准确性。但这为进一步的相关研究提供了方向:通过编程方法建立符合AWSC交叉口规则的仿真模型用以日后的相关研究。
3 结论
交叉口是道路网络中的关键节点,更是交通瓶颈和交通事故的多发点。因此,必须依靠先进的交通管理和控制措施来解决交叉口问题,减少交通延误,提高交叉口通行能力,以适应日益增长的交通需求,从而保证城市交通的安全与畅通。本文在全面了解国内外无信号交叉口研究现状的基础上,利用美国里诺市某AWSC交叉口的视频数据,全面分析了AWSC交叉口中行人与机动车的基本冲突情形,总结出12类基本冲突情形,并将这些基本冲突划分为行人半过街和完全过街两种情况分别进行理论分析建模,并利用现有数据对模型进行验证分析,取得了一定的效果,但是受限于研究时间和个人精力,本研究存在以下不足:
(1)本次研究局限于美国的一个AWSC交叉口,未能对更多同类交叉口进行类比研究分析。
(2)本次研究仅针对行人与机动车12类最基本的冲突情形,未能考虑有多名不同走向行人、多辆机动车时,行人与机动车之间的相互影响。
(3)所建模型受样本量限制,准确度不高。虽然根据交叉口视频统计了3 000多个数据,但真正能够用于验证模型的样本数量仍然较少。
目前我国对于无信号交叉口的研究较为局限,全向停车控制交叉口在国内则更是鲜见。实际上,对于车流量较小的一些城市道路交叉口,设置信号灯只会增大交叉口延误,理应采取无信号控制方式,而停车控制作为无信号控制方式的一种,在减少延误的前提下还在一定程度上降低了机动车通过交叉口的速度,给行人过街创造了有利条件,同时也大大降低了交通事故的发生概率。除了加大推广应用以外,早日建立完备的无信号口相关法律法规也是至关重要的。只有行人、机动车遵循相应的交通规则,交叉口才能充分发挥其通行能力,才能更安全更快捷地为人们的出行提供服务。
