离心力场作用下的燃气轮机压气机叶片振动模态分析
2018-12-20杨博宇殷鸣向召伟殷国富
杨博宇,殷鸣,向召伟,殷国富
离心力场作用下的燃气轮机压气机叶片振动模态分析
杨博宇,殷鸣,向召伟,殷国富
(四川大学 制造科学与工程学院,四川 成都 610065)
分析燃气轮机压气机叶片在离心力场作用下导致的动频相较于无载荷时的固有频率(静频)不同之处,求出叶片工作时的真实振型和共振频率对于提高叶片的动态性能有重要的作用。通过对某重型燃气轮机轴流式压气机某级动叶片的数字化建模和振动模态分析,分别计算得出了压气机叶片在无载荷、离心力场作用下的前六阶固有频率、动频及振型云图,分析了离心力场作用下叶片的应力分布状态,以及离心力场对叶片固有频率的影响。根据转子转速区间,分析了三种不同转速产生的离心力场对叶片频率的影响趋势。计算结果表明:离心力场使叶片产生动力刚化效应,使叶片的各阶动频相较固有频率有所增大;离心力场对基频影响最为显著,当转子转速为6000 r/min时,基频相对偏差达63.73%;动力刚化效应与转子转速呈正相关,叶片转速增大导致动频增大,且基频增大最为显著。
燃气轮机;压气机叶片;离心力场;模态分析;动频
燃气轮机主要由压气机、燃烧室和燃气涡轮三大部分组成。压气机通过提高流过的空气压力,供给燃烧室以符合技术要求的压缩空气,其性能优劣直接影响燃气轮机的功率、耗油率、工作稳定性和可靠性。国内外案例分析表明,绝大多数失效是由压气机叶片疲劳破坏引起,主要原因是:高速旋转的压气机叶片承受极大的离心力、气动力、热应力及空气中沙尘等吸入物的影响,极易出现振动,导致叶片产生疲劳裂纹甚至断裂;为提高燃机的整体效率,增大空气流量和压比,叶片几何外形设计薄而长,导致强度储备降低;当激振力与叶片固有频率相等或成整数倍时,叶片产生共振,严重影响压气机的性能和叶片寿命。因此,研究分析叶片的静频(固有频率)及在各种场作用下的动频显得尤为重要。
国外针对叶片振动的研究起步较早,1982年欧洲就开始制定标准测量方法和性能试验[1],形成“故障模式认知-耐久性设计-损伤模型分析-现代试验方案-理论成果转化”的叶片振动分析与优化体系;1996年美国国家可再生能源实验室(NREL)研制了跟踪测量叶片响应的数据分析采集系统,可远程测量分析叶片的模态数据,极大提高了测量精度和采集效率[2]。21世纪以来,国外研究热点主要集中在叶片振动破坏机理分析、叶片结构优化的实验验证方面。G. C. Larsen[3]通过有限元方法对叶片进行模态分析,提出随着叶片几何形状薄且长的设计趋势,如何避免叶片运转中的振动失稳;P. Malhotra[4]对大型风机叶片进行疲劳载荷试验,得出大型叶片适用于双轴疲劳载荷测试的结论。
我国在叶片振动分析领域的研究起步较晚,为了打破国外长期的技术垄断与封锁,近年来经国家973计划、863计划等项目的大力扶持,特别是被国务院列入重大专项予以优先发展,也取得了一定的研究成果。张利民[5]通过ANSYS软件Solid45、Solid185、Solid95、Solid186四种单元类型以及不同的网格划分精细程度对同一叶片模型进行模态分析,得出了计算精度与选择单元类型、单元边长之间的关系;李静[6]在室温条件下进行一阶弯曲振动疲劳实验,确定了叶片在1×107循环基数下的振动疲劳极限,引入应变比因子对Basquin方程进行了修正;王应军[7]考虑了挥舞振动、摆振振动、扭转振动三种情况,分别计算了某空心和实心风机叶片的固有频率并进行对比,分析了不同振动形式对叶片产生的不利影响。
本文利用三维绘图软件Pro/E、UG NX以及有限元分析软件ANSYS WorkBench,对某重型燃气轮机轴流式压气机某级动叶片进行振动模态分析,分别得出压气机叶片在无载荷、离心力场作用下的前六阶固有频率、动频及振型云图,分析离心力场对叶片固有频率的影响,为压气机叶片的共振分析、叶型改进提供依据。
1 叶片几何模型及有限元模型的建立
1.1 叶身几何模型的建立
为满足强度和气动性能的要求,叶身多采用与亚音速、超音速流动相适应的叶型,按一定的扭向规律以及叶型重心径向分布规律沿叶型积叠轴累加形成。本实验模型叶身为弧形,出气侧叶高255.86 mm,叶身至转子中心线平均直径939.64 mm,弦长73.83 mm,由13条截面曲线生成,各曲线为沿辐射线方向依次通过各截面且没有突变的光滑曲线。本模型由设计叶身尺寸编制ibl文件,导入Pro/E软件通过“边界混合”命令生成叶身几何外形。
1.2 榫头几何模型的建立
叶片榫头为枞树形,顶部为曲面,由12个不同测点高度的曲线拟合生成。相比其他形式榫头,其尺寸小、质量轻、承载能力强,广泛应用于压气机始末两级叶片形式。在UG 7.5软件中建立不同测点高度的曲线轮廓,通过“沿变截面扫略”及“通过曲线组”命令生成榫头模型,同时将叶身模型导入榫头模型,通过布尔运算等命令组成叶片模型如图1所示。

图1 叶片几何模型
1.3 叶片有限元模型的建立
将叶片几何模型通过“*.x_t”格式文件导入ANSYS软件中,采用由20个节点定义的Solid 95单元进行网格划分,该单元具有塑性、蠕变、辐射膨胀、应力刚度、大变形以及大应变的能力,同时在模型有不规则形状时不会降低计算精度,故适合叶片模型的网格划分。叶片模型共划分为98011个网格、162843个节点。
2 模态分析基本理论
叶片在各种影响因素作用下的振动过程可表示为内力、外力和惯性力的平衡方程组[8-9]:

式中:为质量矩阵;为阻尼矩阵;为刚度矩阵;()、()、()、()分别为加速度列阵、速度列阵、位移列阵、激振力列阵。
式(1)是一组耦合方程组,当系统自由度较大时,求解很困难,因此考虑将耦合的微分方程组转化为独立方程组,即以各阶主振型对应的模态坐标代替物理坐标,简化求解过程[8]。
叶片承受激振力可近似认为周期性变化,即:
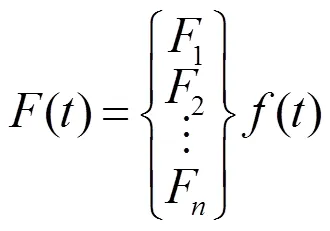
将周期函数()展成傅氏级数,即:

式中:0、a、b为傅氏系数。
引入正则振型A、正则刚度矩阵K、正则坐标X、正则阻尼矩阵R,对式(1)进行解耦,得第阶有阻尼稳态响应为:

式中:β为放大因子;Ψ为相位角。
又由于不相等的固有频率的两个主振型关于刚度矩阵和质量矩阵正交,则:

式中:ω为各阶固有频率值。
由此求得正则刚度矩阵K的对角线元素即各阶固有频率的平方值[8]。
实际工况下,考虑叶片受离心力场的影响,出现动力刚化效应,进而影响叶片的振动模态。
3 压气机叶片材料性能分析
叶片材料的选择原则是:选择能够承受工作温度下工作载荷的轻质材料,即较高的比强度是叶片选材的关键[10]。从初级动叶片至末级动叶片,材料的种类依次为:铝合金、沉淀不锈钢、钛合金、高温合金。从目前的叶片发展趋势看,钛合金由于良好的比强度,有逐渐取代铝合金以及沉淀不锈钢,成为前几级压气机叶片首选材料的趋势,而后几级叶片由于工作温度太高,钛合金材料的抗氧化能力以及阻燃性能通常不能胜任,多选用高温合金材料。
本压气机某级动叶片采用MAR-M002材料,是镍基沉淀硬化型等轴晶铸造高温合金,材料密度8.5×103kg/m3,室温硬度HBS 360~370,使用温度在1000℃以下。该合金的组织稳定,抗高温氧化和耐热腐蚀性能较好,但因含有较多的钨、钽和铪元素,所以与其他等轴晶铸造镍基高温合金相比,密度较大,适于制作1000℃以下工作的涡轮转子叶片和整铸涡轮盘。
MAR-M002在不同温度下的弹性模量(×109N/m2)、热导率(W/(m·℃))、线膨胀系数(×10-6/℃)、泊松比、抗拉强度σ(MPa)、断面收缩率(%)如表1所示[10]。
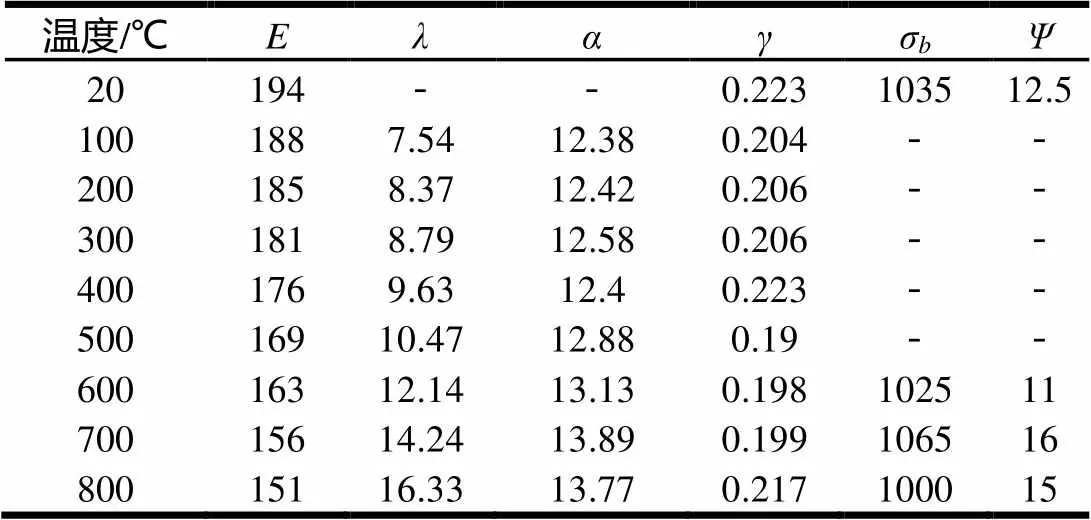
表1 MAR-M002在不同温度下的材料性能参数
4 压气机叶片模态分析
4.1 叶片固有频率分析
由于叶片的枞树形榫头固定在压气机轮毂上的叶片槽中,刚度很大,可作为固定约束处理,进行模态分析。计算结果如表2及图2所示,前六阶固有频率呈逐渐增大趋势,且叶片除前两阶振动为弯曲振动外,其余各阶均为弯扭复合振动。
4.2 叶片在离心力场作用下的动频分析
离心力作为一种体积力(彻体力),其与质量、质量所处的半径以及转速的平方成正比。在旋转叶片中,离心力主要产生径向拉应力,使扭转叶片产生扭转应力,此外由于叶型及榫头各截面的质心一般不在同一条转子旋转中心线上,离心力还会产生弯曲应力。因此,在离心力场作用下,叶片的频率会发生改变。
分析离心力场对叶片模态的影响,按转子转速区间,给叶片分别施加绕转轴(轴)628.3 rad/s(6000 r/min)、837.8 rad/s(8000 r/min)、1047.2 rad/s(10000 r/min)的旋转角速度,对叶片的枞树形榫头施加远端位移约束,限制、、方向的平动和绕、轴的转动,对叶片进行静态结构分析,得到叶片的离心应力分布如图3所示,再以离心应力为预应力对叶片进行模态分析。当转子转速为6000 r/min时,在离心力场作用下,叶片的前六阶动频及振型如图4所示。
由图3可见,从榫头至约2/3叶高处离心应力在局部范围内呈均匀散布,叶顶所受离心力极小,且随着叶片转速的增大,最大应力值明显增大,但离心应力分布范围基本保持不变。
由图2、图4及表2可见,以转子转速6000 r/min为例,叶片在离心力场作用下的振型与无载荷时的振型相似,各阶动频相较固有频率呈增大趋势,其中一阶频率变化最大,绝对偏差达105.42 Hz,相对偏差达63.73%,且相对偏差呈逐渐减小趋势。此种现象的产生是因为叶片在高速旋转时,其上的任一质量微元都受到离心力的作用,在叶片振动过程中,离心力产生使质量微元回到平衡位置的趋势,即增加了叶片的弹性恢复力,使其产生动力刚化效应,从而使叶片的各阶频率增大。由此可见,离心力场增大了叶片的频率且对基频影响最大。
由表2可知,当压气机叶片以三种不同转速运转时,随着转子转速的增大,叶片各阶动频、各阶绝对偏差、各阶相对偏差都呈增大趋势且增幅明显,当转子转速为10000 r/min时,一阶动频达到固有频率的1.24倍,增幅最大。由此可见,叶片转速越快,动力刚化效应越明显,叶片动频增大越显著,尤以基频为甚。

图2 叶片固有频率及振型云图

表2 叶片的固有频率和6000、8000、10000 r/min离心力场作用下的动频
5 小结
本文对某重型燃气轮机轴流式压气机某级动叶片进行振动模态分析,分别计算了叶片在无载荷、离心力场作用下的前六阶固有频率、动频和振型云图,分析了离心力场作用下叶片的应力分布状态以及离心力场产生的动力刚化效应对叶片固有频率的影响。此外,根据转子转速区间,分析了三种不同转速产生的离心力场对叶片频率的影响趋势。得出以下结论:
(1)无载荷时,叶片前六阶固有频率呈逐渐增大趋势,且叶片除前两阶振动为弯曲振动外,其余各阶均为弯扭复合振动。
(2)离心力场作用下,叶片主要承受径向拉应力、扭转应力、弯曲应力,对叶片的固有频率产生影响。叶片在高速旋转时,因为离心应力的影响,增加了叶片的弹性恢复力,使其产生动力刚化效应,使叶片的各阶动频相较固有频率有所增大。
(3)离心力场对基频的影响效果最为显著,当转子转速为6000 r/min时基频相对偏差达63.73%。
(4)离心应力在叶身局部范围内呈均匀散布,叶顶所受离心力极小,且随着转子转速的增大,离心应力分布范围基本保持不变,但最大值增大明显。
(5)叶片转速越快,动力刚化效应越明显,叶片动频增大越显著,尤以基频为甚。

图3 叶片的离心应力分布云图

图4 离心力场作用下叶片的动频及振型云图(转速6000 r/min)
[1]Larwood Scott,et al. Ned Wind 25 blade testing at NREL for the European standards measurement and testing program. No. NREL/TP-500-29103,National Renewable Energy Lab., Golden, CO (US),2001.
[2]Musial W D,Clark M E,Stensland T. Application of BSTRAIN software for wind turbine blade testing[R]. National Renewable Energy Lab., Golden, CO (United States),1996.
[3]Larsen G C,Hansen M H,Baumgart A,et al. Modal analysis of wind turbine blades[R]. 2002.
[4]Malhotra P. Advanced blade testing methods for wind turbines[J]. 2010.
[5]张利民,王克明,吴志广. 叶片模态分析的单元类型选择[J]. 沈阳航空航天大学学报,2011,28(2):21-24.
[6]李静,孙强,李春旺,等. 某型航空发动机压气机叶片振动疲劳寿命研究[J]. 应用力学学报,2011,28(2):189-193.
[7]王应军,裴鹏宇. 风力发电机叶片固有振动特性的有限元分析[J]. 华中科技大学学报(城市科学版),2006,23(2):44-46.
[8]闻邦椿,刘树英,张纯宇. 机械振动学[M]. 北京:冶金工业出版社,2000.
[9]陈克非,戴运平,汪锐. 高炉煤气余压发电透平机转子叶片的断裂分析[J]. 机械,2010,37(10):72-75.
[10]《中国航空材料手册》编辑委员会. 中国航空材料手册(第二版)第二卷[M]. 北京:中国标准出版社,2002.
The Vibration Modal Analysis of Compressor Blades of Gas Turbines under the Influence of Centrifugal Force Fields
YANG Boyu,YIN Ming,XIANG Zhaowei,YIN Guofu
( School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, China )
The calculation of mode shapes and resonant frequencies of compressor blades of gas turbines in working conditions, as well as the analysis of differences between the dynamic frequencies under the influence of centrifugal force fields and the natural frequencies (static frequencies ) of compressor blades, plays an important role in improving the blades' dynamic properties. In this paper, the vibrational frequencies and mode shapes of compressor blades from 1st to 6th order in load free and centrifugal force fields conditions are calculated separately by digital modeling and vibration modal analysis for moving blades of a certain axial-flow compressor of a heavy-duty gas turbine. The stress distribution as well as the natural frequencies of blades under the influence of centrifugal force fields is analyzed. The effect trends caused by centrifugal force fields which are generated in three different rotational velocities for blades' vibrational frequencies are analyzed. The result shows that: Centrifugal force fields cause the dynamic stiffening for blades which makes their dynamic frequency greater than the natural one in each order; Centrifugal force fields have the most significant impact on the fundamental frequencies of blades, for instance, when the blade's rotational velocity reaches 6000rpm, its relative deviation about fundamental frequency can achieve 63.73%; The dynamic stiffening is positively correlated with the blades' rotational velocities, and the greater rotational velocity causes the greater dynamic frequency, especially in the fundamental frequencies of blades.
gas turbine;compressor blade;centrifugal force field;modal analysis;dynamic frequency
TH113.1
A
10.3969/j.issn.1006-0316.2018.11.008
1006-0316 (2018) 11-0031-06
2018-01-09
四川省科技支持计划项目(2016GZ0001);中央高校基本科研业务费专项资金资助(2015CDDY-S08-SCU)
杨博宇(1988-),男,辽宁抚顺人,硕士研究生,助理工程师,主要研究方向为叶片增材制造、熔模铸造、模态分析;殷国富(1956-),男,四川西充人,教授,博士生导师,主要研究方向为制造自动化、智能设计技术、CAD/CAM/CIMS。
