一种单层囊式空气弹簧的隔振分析
2018-12-20宁小刚王泽荫车麒麟
宁小刚,王泽荫,车麒麟
一种单层囊式空气弹簧的隔振分析
宁小刚,王泽荫,车麒麟
(甘肃机电职业技术学院,甘肃 天水 741000)
空气弹簧是一种理想的非线性隔振元件,其容易实施主动控制,具有优良的刚性非线性特性,能有效抑制振动、缓冲减振。以某型囊式空气弹簧为研究对象,基于ABAQUS建立有限元模型,并对充气到0.7 MPa过程和压缩10 mm过程进行了模拟仿真,得出应力应变云图,借助-曲线图分析了空气弹簧垂向力学特性,并对刚度进行了曲线拟合。最后基于MATLAB对空气弹簧的隔振性能进行了分析,得出其可以将外界简谐激励的振幅由10 mm降低到2 mm左右,具有良好的隔振性能。
空气弹簧;隔振;有限元分析
空气弹簧是一种非金属弹簧,结构包括上、下盖板和橡胶气囊体,其中橡胶气囊体的内部为层状结构,包括橡胶内层、橡胶外层、帘线层等。通常情况下,橡胶和帘线本身不能承载负荷,而是由胶囊体内的压缩空气来承担。工作时,向胶囊体气腔内冲入压缩空气,凭借压缩空气在受压时产生的反作用力作为弹性恢复力而进行隔振。实际使用中,空气弹簧主要承受垂直载荷。空气弹簧具有柔性和扩展性,可以根据其承受外界负载的大小变化来调整空气弹簧内部的空气压力。
1 空气弹簧的隔振特点
与普通的弹簧相比,空气弹簧对振动隔离具有以下特点[2]:
(1)可控的刚度和阻尼,呈现典型的非线性。刚度随外界载荷的变化而改变,并且在任何载荷下所具有的自振频率几乎是恒定的。
(2)较大的有效承载力。可通过控制其内部初始气压大小来调节承载力,如要增加承载力则可在限度范围内增大初始气压。
(3)高度可控,通用性较好。可通过调节其高度就可以满足不同场合的应用。
(4)良好的吸收振动和降噪性能。由于工作介质是空气,因而不仅能吸收振动,还能有效缓冲冲击载荷,除此之外,因其自身内摩擦很小而几乎没有噪声。
(5)重量较轻。由于气囊体内的空气质量可忽略不计,气囊体本身质量又很小,因此整个元件只有上盖和下座有重量,相比其他弹簧,其总体上重量很小。
(6)与金属弹簧相比,具有较长疲劳寿命。
2 空气弹簧的选型
选用西安晨光橡胶有限公司086060H-1型号的H活套式空气弹簧(单曲),如图1所示。空气弹簧能够自行密封;腰环为钢制、焊接而成;法兰采用铝合金或钢制;密封端板与产品配合的面光滑平整,强度足够,承受载荷不变形,但不包含在组件内;其他附件包括有高强度螺栓M10和与之配套的螺母及锁紧垫圈。
3 基于ABAQUS的有限元分析
3.1 空气弹簧FEA特点
空气弹簧涉及空气及橡胶两种物质,有限元分析(Finite Element Analysis)具有以下特点:①空气弹簧是由腔体内的空气及外部橡胶、上下盖板、橡胶内部的帘线层等众多材料组成,是一个典型的系统分析模型;②涉及气体、固体两个不同属性的物质,是个典型的流-固耦合问题;③涉及复杂的材料定义,既有线弹性材料、超弹橡胶材料(视为各向同性),又有帘线层帘子布材料(视为各向异性);④本身是个复杂的装配系统,有接触、变形,涉及众多非线性问题。

图1 空气弹簧外形
3.2 空气弹簧的非线性问题[1]
(1)材料非线性。因胶囊体是由橡胶制成的,橡胶属于超弹性材料,且胶囊体中存在着轴向刚度较大的帘线层,具有非线性、粘弹性、非均质和各向异性的性质,所以这就需要采用非线性材料来描述。
(2)几何非线性。在使用中,对于产生很大挠曲变形的橡胶气囊体,传统的小变形理论不再适用,则需采用大变形理论,所以就需要考虑几何非线性。
(3)边界非线性。在使用中,空气弹簧具有较大横向位移,胶囊体与上、下盖板的接触面积会产生较大变化,所以要考虑边界非线性。
(4)空气压缩非线性。由于空气弹簧是依靠胶囊体内部的空气来工作的,所以为了平衡外部的负载,胶囊体内的空气压力在不断变化,因而必须考虑空气流体压缩非线性。
3.3 空气弹簧的模型建立
采用4节点壳减缩单元(ABAQUS中定义为S4R),每个节点有6个自由度。由于帘线的力学性能往往决定橡胶气囊体的性能,可用Rebar模拟帘线层,几何特性参数定义为:Reba的横截面积为1 mm2,在同一层内Rebar与Rebar间距为3.5 mm,Rebar距橡胶材料的壳单元中性面距离为±1 mm。则橡胶气囊的有限元模型可通过壳单元和Rebar定义出来。对于上下盖板采用刚体壳单元R3D3(三维三节点)和R3D4(三维四节点),对于胶囊体中的空气流体采用膜壳流体单元SFM3D3和SFM3D4。
胶囊体为橡胶帘线复合材料;空气弹簧的上、下盖板为钢板材料,因其变形相对胶囊体来说很微小,可以看成刚性材料。钢板的材料参数为弹性模量=210 GPa,泊松比=0.3,dens=7.8e3;橡胶体的材料特性参数为C10=3.2e6,C01=0.8e6,dens=1000。
胶囊体和盖板的接触条件为壳单元和刚性曲面的接触。由于实际的空气弹簧盖板与胶囊体接触时摩擦力很大,认为胶囊体和盖板接触时无相对滑移。
综上,建立空气弹簧有限元半模型如图2所示。其中,由于橡胶囊体部分是重点,为了使计算结果更为合理,所以在经线方向上把胶囊体与上、下盖板可能接触的部分进行了适当的网格加细。

图2 空气弹簧有限元半模型
3.4 空气弹簧的分步分析
采用ABAQUS/Standard模块进行空气弹簧非线性静特性分析。先将上、下盖板刚体约束住,再向气体单元加上0.7 MPa的工作气压使其进入工作状态,得到在充气0.7 MPa时空气弹簧的应力和应变如图3所示。接着在保持其余方向约束不变的情况下,释放上盖板刚体所施加的垂向位移约束,并施加向下压缩10 mm的垂向位移,得到空气弹簧向下压缩10 mm后的应力和应变如图4所示。由于本文空气弹簧工作在受压状态,几乎不受拉力,所以无需对空气弹簧进行在受拉状态下的应力应变分析。

图3 充气0.7 MPa时的应力应变云图

图4 压缩10 mm时的应力、应变云图
3.5 空气弹簧的垂向力学特性分析
基于ABAQUS/Viewer读入分析数据,根据-曲线图分析空气弹簧的垂向力学特性。在充气和压缩过程中橡胶气囊内空气体积随时间变化曲线如图5所示;充气过程中,空气弹簧的体积随时间呈非线性增大,体积变化率起初较大、再逐渐变小;压缩过程中,空气弹簧的体积随时间呈非线性减小,变化率先缓后快。空气弹簧压缩过程中的压强-位移曲线如图6所示,气腔内的压强随着位移的增大而呈非线性增大,增长变化率起初缓慢、然后逐渐加大。

图5 体积-时间曲线图

图6 压缩过程的压强-位移曲线图
空气弹簧是典型的变刚度隔振元件,刚度对整个隔振系统来说是非常重要的参数。理论上,空气弹簧在初始内压状态下,随着垂向位移的改变,内压和刚度会跟着改变。本文先给空气弹簧0.7 MPa初始内压、再垂向施加一个压缩10 mm向下位移时,得到参考点的作用反力与位移的变化关系曲线如图7所示,在压缩过程中载荷-位移呈现一条曲线、刚度呈非线性变化,但曲线的变化趋势跟直线很近似,说明空气弹簧没有产生太大的非线性,这与本文选取的空气弹簧结构有关。
通过对曲线进行线性拟合,可求得空气弹簧的稳定刚度(即拟合直线的斜率),进行线性拟合后的载荷-位移变化曲线如图8所示,其中一次函数=23000+310的斜率就是空气弹簧的稳定刚度。
4 空气弹簧的隔振分析
本文给空气弹簧隔振系统施加一个单频简谐激励(),研究其隔振对象的运动状态。隔振系统模型如图9所示。
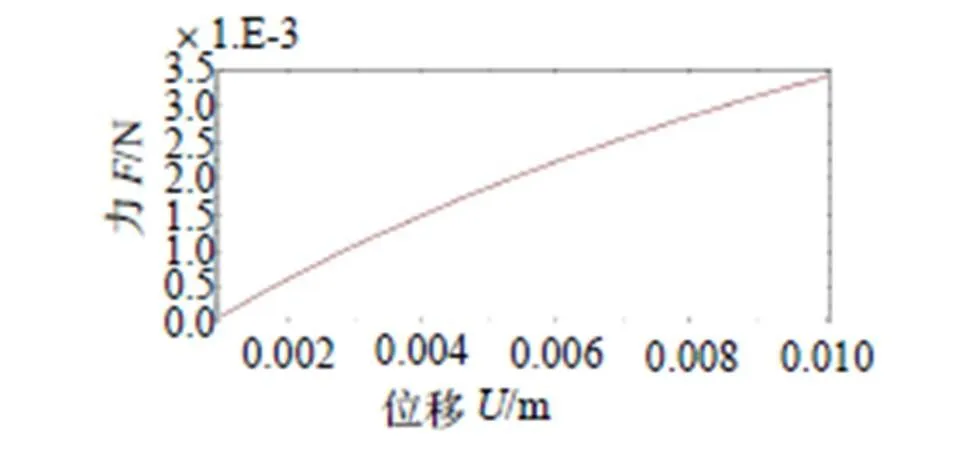
图7 压缩过程中载荷-位移的变化曲线

图8 压缩过程中载荷-位移变化的拟合曲线
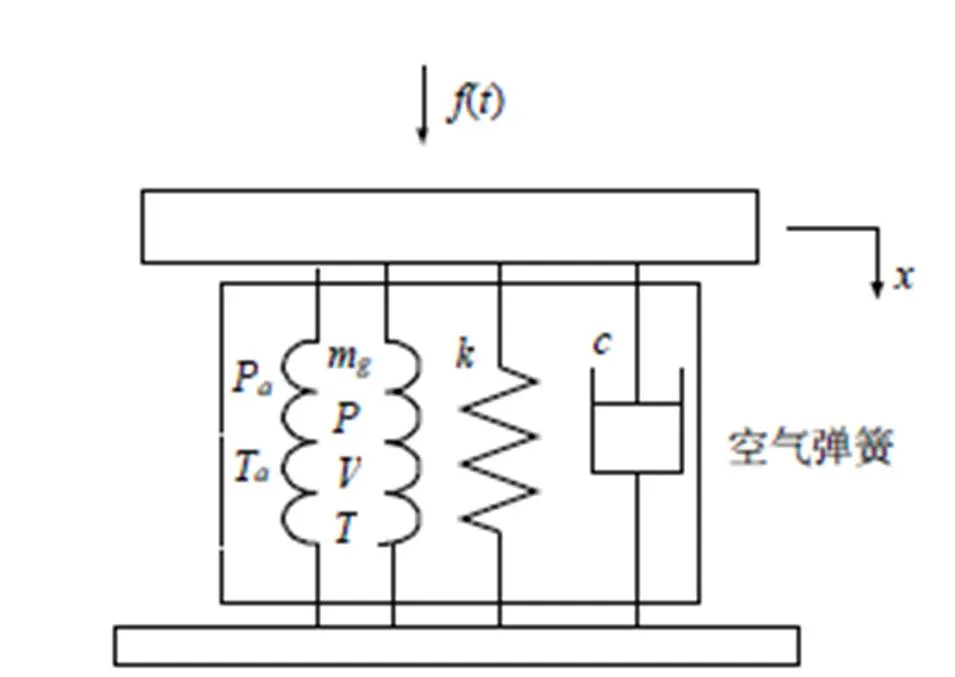
图9 空气弹簧隔振系统的动力学模型
根据模型图,系统动力学方程[3]为:

式中:为气腔内压力,MPa;p为大气压力,MPa;为气体有效作用面积,m2;为载荷质量,kg;为隔振对象位移,m;为激振力,N;为阻尼,N·s/m;为刚度,N/m。
设腔内为理想状态气体,其状态方程为:
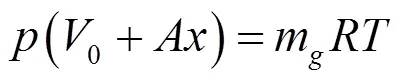
式中:0为空气弹簧初始容积,m3;为在不考虑面积变化的情况下,空气弹簧容积面积,与气体有效作用面积相等,m2;m为气腔内气体质量,kg;为空气气体常数,J/(kg·K);为腔内气体温度,K。
利用MATLAB进行空气弹簧仿真,如图10所示,仿真模型中的各参数如表1所示。

图10 MATLAB仿真模型

表1 仿真模型的计算参数
仿真模型中,设外界激励为()=0sin,其激励幅值取0=0.01 m、频率取=50 rad/s,在此激励下,经空气弹簧系统隔振后的位移-时间输出如图11所示。
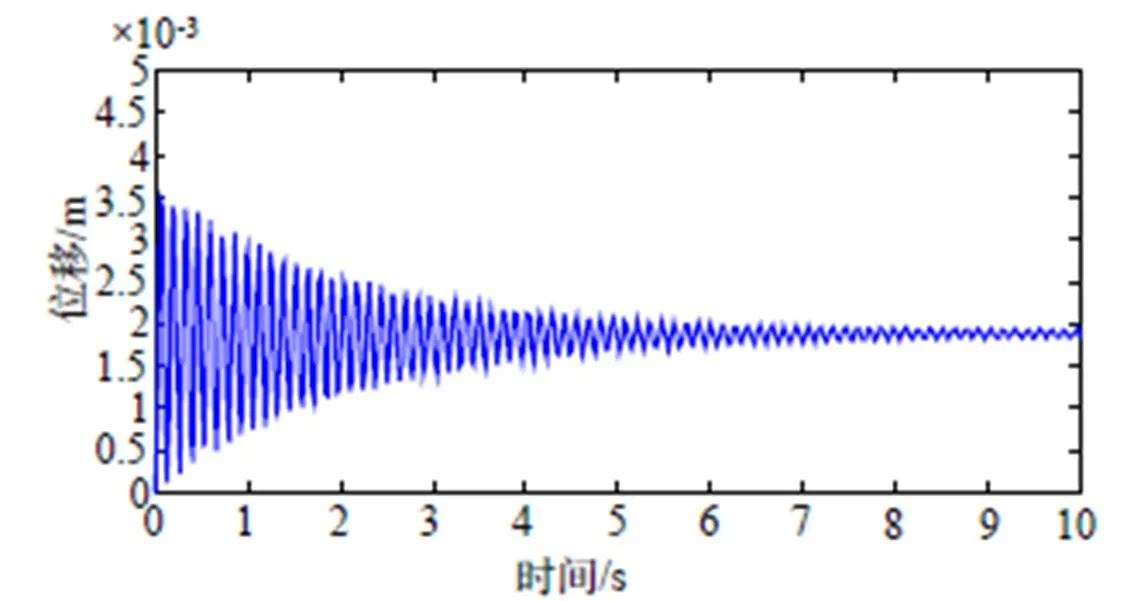
图11 系统在正弦激励下的x-t图
从图11可以看出,在外界的正弦激励作用下,空气弹簧明显衰减了振动,当其在达到稳态时幅值保持在2 mm左右,相对10 mm的幅值来说,隔振效果明显。
5 结论
(1)空气弹簧在充气过程中-呈非线性增大、变化先快后慢,在压缩过程中-呈非线性减小、变化先慢后快,-呈非线性增大、变化先慢后快。
(2)空气弹簧在压缩过程中载荷-位移呈现一条曲线,刚度呈非线性变化。
(3)空气弹簧将外界简谐激励振幅由10 mm降低到2 mm左右,具有良好的隔振性能。
[1]陆晓黎,上官文斌. 车用空气弹簧力学特性研究与有限元分析[D]. 广州:华南理工大学,2011.
[2]张旗,孙景工. 空气弹簧动力学特性分析[D]. 天津:军事医学科学院卫生装备研究所,2011.
[3]张锦光,陈娟,等. 电磁-空气弹簧混合隔振器的设计与仿真[J]. 武汉理工大学学报,2015(10):391-394.
Vibration Isolation Analysis of ASingle - layer Cystic Air Spring
NING Xiaogang,WANG Zeyin,CHE Qilin
( Gansu Mechanical& ElectricalVocational College, Tianshui 741000, China )
Air spring is an ideal nonlinear vibration isolation element. It is easy to implement active control, has the excellent rigidity nonlinear characteristic, can restrain the vibration effectively, cushioning the vibration. In this paper, a type of cystic air spring is used as the research object, the finite element model was established based on ABAQUS, carried out the simulation for the process of filling up to 0.7MPa and compressing 10mm,and obtained the stress strain cloud diagram. The vertical mechanical properties of air spring were analyzed by x-y curve, and the stiffness was fitted. Finally, based on MATLAB, the vibration isolation performance of air spring is analyzed, and it is concluded that the amplitude of the external harmonic excitation can be reduced from 10mm to about 2mm, with good vibration isolation performance.
air spring;vibration isolation;finite element analysis
TB535+.1
A
10.3969/j.issn.1006-0316.2018.11.011
1006-0316 (2018) 11-0045-05
2018-05-18
宁小刚(1991-),男,甘肃天水人,硕士,助理讲师,主要研究方向为汽车零部件。
