航向信息辅助的MIMU/GPS高精度组合导航方法

杨 波，单 斌，王跃钢，张复建，薛 亮

（火箭军工程大学 控制工程系，西安 710025）

近些年来，随着微机械技术的日益成熟，微机械惯性器件在民用、军用等领域内的应用越来越广泛。利用微机械陀螺仪与加速度计构成的微惯性测量组合（MIMU）具有成本低、体积小、能耗低、重量轻、寿命长、抗高过载和环境适应能力强等突出优点[1]。但是，MIMU导航普遍存在着精度低、误差快速发散的突出问题。解决该问题的有效措施之一是，将MIMU与GPS进行组合导航，不仅能有效抑制MIMU导航误差发散、实现较高导航精度，而且能有效解决卫星定位异常突变等问题[2]，使两者性能互补、实现更优越的系统性能。

目前，MIMU/GPS组合导航多采用位置+速度组合模式，即所谓的松组合[2-5]，选取 MIMU导航输出的位置、速度与GPS输出的对应信息相减作为量测，采用卡尔曼滤波设计组合导航算法。但是，当受到外部环境等因素影响，GPS接收机所收到的卫星颗数可能少于四颗，此时接收机显然无法定位，也就无法与MIMU实现组合导航。而一旦失去GPS的辅助，MIMU导航的误差将会快速积累。对此，文献[6-7]认为采用伪距+伪距率组合模式，即所谓的紧组合，可以有效应对有效卫星少于四颗时GPS无法定位的问题。从公开文献来看，目前紧组合用于MIMU/GPS组合导航的研究不多，而且紧组合的滤波计算量明显相对较大。同时，由于微机械惯性器件的误差较大，导致MIMU/GPS组合导航的航向误差通常较大甚至出现发散的情况[8]。为此，文献[8-9]研究了采用磁强计辅助MIMU/GPS进行组合导航的方法，但是磁航向角容易受到外部磁场环境和设备内部电磁干扰环境的影响。文献[10]研究了利用双天线GPS提供航向角信息，辅助MIMU提高航向精度的方法，该方法要求两个天线间隔一定距离（即基线长度），而且基线越长航向精度越高，显然在诸如制导炮弹等小型载体上难以安装间隔较长距离的两个天线。

因此，本文研究基于紧组合模式的 MIMU/GPS组合导航方法，以解决卫星少于四颗时GPS无法定位的问题，并为了降低滤波计算量，仅利用GPS输出的伪距来辅助MIMU进行导航；针对组合导航过程中航向精度较低甚至发散的问题，以车辆、导弹、火箭弹等载体为应用背景，根据GPS输出的水平速度计算获得伪航向角，利用其辅助MIMU/GPS组合导航以提高航向精度。

1 航向信息辅助的MIMU/GPS组合导航方案

导航坐标系采取东北天地理坐标系。在 MIMU/GPS组合导航系统中，MIMU和GPS对载体的运动参数分别独立进行测量，MIMU经导航解算后输出载体的速度、位置和姿态信息，GPS接收机可输出伪距、伪距率、速度、位置以及星历数据等信息。选取MIMU导航解算误差与GPS误差作为状态，利用MIMU导航解算获得的位置信息与 GPS的星历数据构造等效伪距，将其与GPS输出的伪距对应相减作为组合导航量测之一；利用GPS输出的水平速度信息计算获得伪航向角，将MIMU导航解算获得的航向角与该伪航向角相减作为量测之二；采用卡尔曼滤波设计组合导航滤波器，将两组量测同时送入滤波器中进行滤波计算，获得系统各种误差的最优估计值；利用该估计值实时地对MIMU导航解算值进行误差校正，并将校正后MIMU输出的导航参数作为组合导航系统的输出。因此，航向信息辅助的MIMU/GPS组合导航原理框图如图1所示。

2 组合导航系统误差模型

在MIMU/GPS组合导航滤波算法设计中，将采用间接法滤波，即以系统误差作为状态，经过滤波计算获得系统误差状态的最优估计值。因此，需要分析建立MIMU导航解算的误差模型以及GPS的误差模型。

2.1 MIMU导航解算的误差模型

由于存在惯性器件误差、安装误差以及初始条件误差等，使得MIMU导航解算结果出现较大误差。其中，安装误差可以进行标定补偿，初始条件误差与初始对准、参数装订有关，惯性器件误差则是MIMU最主要的误差，因此文中重点考虑惯性器件误差。

对于微机械加速度计的误差，经实验标定补偿后主要剩下随机误差，一般主要考虑随机常值误差和白噪声[11]。因此，加速度计误差模型可建立如下：

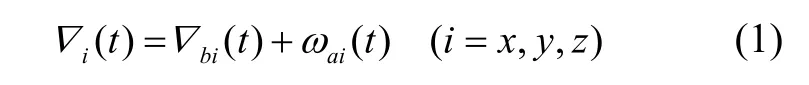
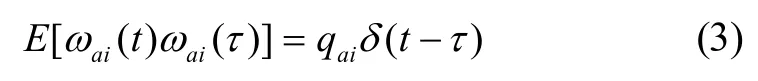
相比于加速度计误差带来的影响，陀螺仪误差对MIMU导航精度的影响更大。对于微机械陀螺，经标定补偿后，通常可采用一阶马尔可夫过程进行描述[11-12]，即陀螺误差模型为

由于惯性器件存在测量误差，这就导致 MIMU导航解算结果存在误差，具体包括数学平台姿态误差、速度误差和位置误差，这些误差的方程形式与传统捷联惯导系统的误差模型一致，本文在此就不再赘述。

2.2 GPS的误差模型

GPS的误差主要表现在测距误差上，引起测距误差的因素主要有卫星钟误差、星历误差、电离层延迟误差、对流层延迟误差、多路径误差、接收机噪声等。其中，GPS的大部分误差都可以从导航电文中提取信息进行校正，但经过校正仍然会存留一些随机误差。这些残存的随机误差都可以等效成时钟误差。

GPS时钟误差所引起的等效伪距误差δρ通常可模型化为[12]

式中，δσ为GPS的伪距率误差，wρ为等效伪距白噪声。

而GPS的伪距率误差则主要由GPS时钟频漂所引起，时钟频漂所引起的伪距率误差通常可模型化为[12]

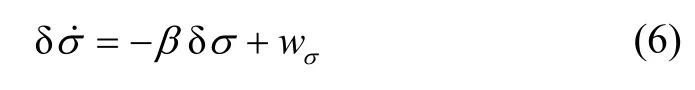
式中，β为反相关时间常数，wσ为伪距率白噪声。

3 航向信息辅助的MIMU/GPS组合导航算法

3.1 组合导航状态方程

采用间接法滤波设计MIMU/GPS组合导航算法，即选取系统误差作为滤波器的状态。根据前面分析，将MIMU导航参数误差、惯性器件误差以及GPS的伪距、伪距率误差作为MIMU/GPS组合导航滤波器的系统状态，即

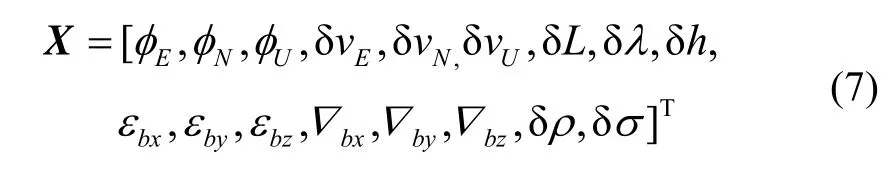
根据MIMU导航解算误差模型与GPS误差模型，可列出MIMU/GPS组合导航系统状态方程为

3.2 组合导航量测方程

由于MIMU/GPS组合导航采用紧组合方式，因此首先需要根据MIMU的导航输出和GPS卫星星历数据来构造等效伪距。设MIMU导航输出的位置信息为，卫星i的位置为则MIMU导航输出对应于卫星i的等效伪距Miρ可利用式(9)来计算：

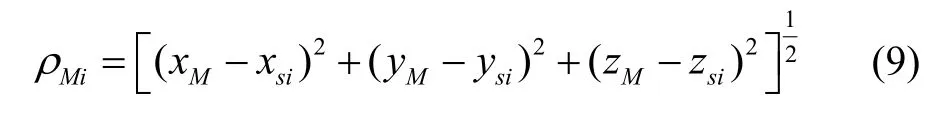
将MIMU导航输出对应的等效伪距与GPS实时输出的伪距对应相减作为 MIMU/GPS组合导航的量测之一。设GPS导航输出的卫星i伪距为ρi，则MIMU/GPS组合导航对应于卫星i的量测 Zi为

记GPS的伪距误差为δρ，GPS的伪距量测白噪声为ivρ，则GPS实际输出的伪距iρ为

相对于载体真实位置 x、y、z，将式(9)展成泰勒级数，并取前两项可得：

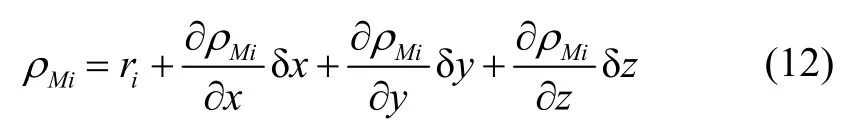
式中，

(3)测量误差会导致单项结构误差的辨识精度浮动，但结构误差的整体辨识精度并未下降，证明了线性化误差模型的稳定性。

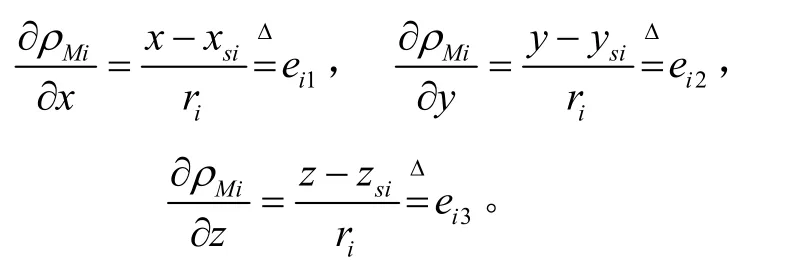
从而，将式(11)(12)代入到式(10)中，可得对应于卫星i的量测 Zi为

根据地球坐标系与地理坐标系之间转换关系有

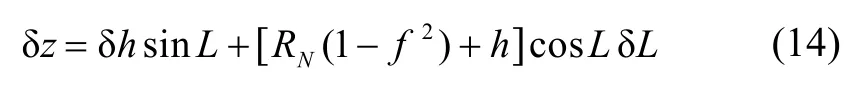
将式(14)代入到式(13)中可得：

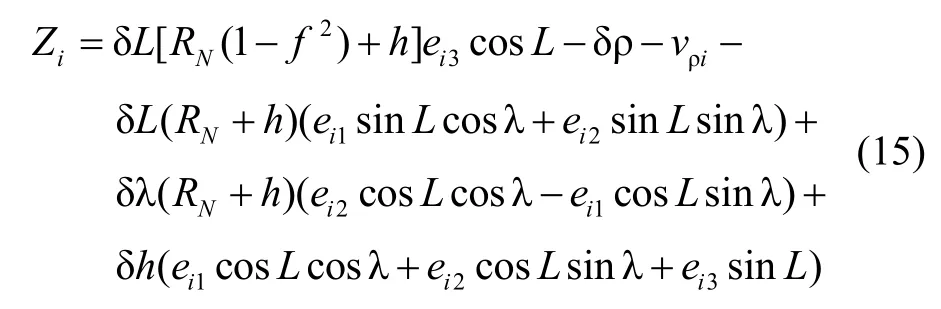
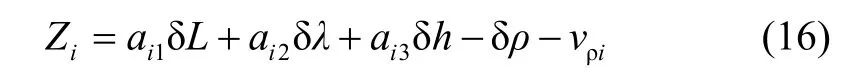
由于微机械惯性器件的误差较大，而且MIMU数学平台天向误差角可观测性较弱，从而导致MIMU/GPS组合导航的航向误差通常较大甚至出现发散的情况，为此需要引入航向信息以辅助提高组合导航的航向精度。

设GPS输出的载体东向、北向速度分别为 vEG、则载体速度与北向的夹角Gψ为

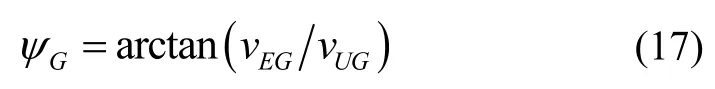
MIMU导航解算获得的航向角ψI是载体纵轴与北向的夹角，当载体速度方向与纵轴方向一致时，角ψG与ψI可视为一致；当载体速度方向与纵轴方向不一致时，两个角之间则存在一个侧滑角。而对于车辆、导弹、火箭弹等运载体而言，其在实际运动过程中鲜有大角度机动，因此侧滑角通常为小角度，对于航向精度要求不高的场合，此时可以将载体速度与北向的夹角ψG视为伪航向角，用来辅助组合导航提高航向精度。

从而，可以利用GPS输出的水平速度信息计算获得伪航向角ψG，将MIMU导航解算获得的航向角与该伪航向角相减作为组合导航量测之二，即

设MIMU导航解算获得的航向角其误差为δψI，GPS输出信息获得的伪航向角其误差为δψG，则根据式(18)可得：

根据 MIMU导航解算的航向角误差与其数学平台姿态误差角之间的关系有

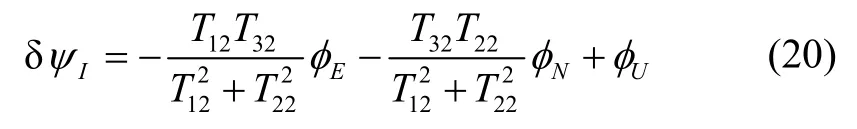
将式(20)代入到式(19)中可得组合导航量测之二为

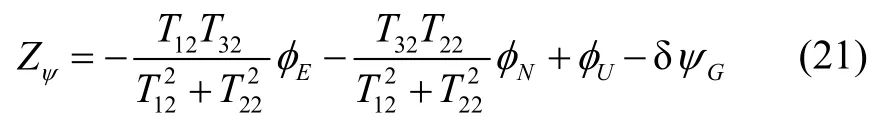
从而，假设GPS接收机能够输出N颗卫星的星历数据与伪距信息，则根据式(9)(10)可以构造出N个量测值 Zi，再将这N个量测值与根据式(18)构造获得的量测Zψ组成一个列向量，作为MIMU/GPS组合导航的量测向量，即：

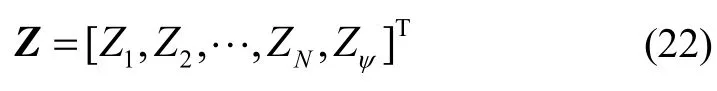
将式(16)和(21)代入到式(22)中可得：

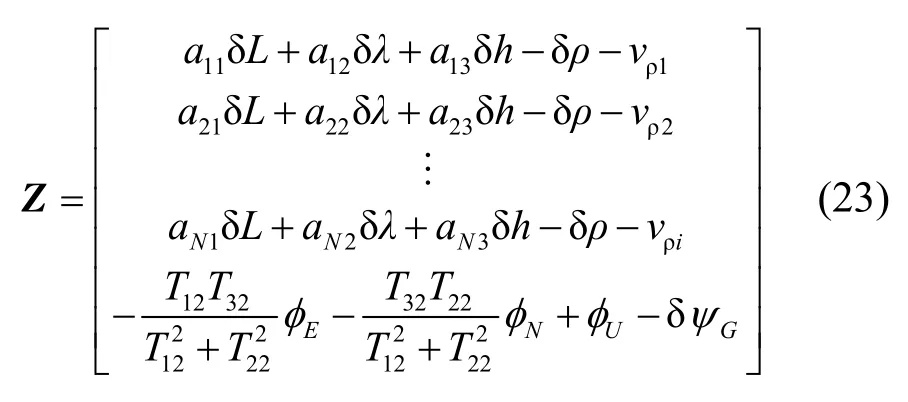
于是，根据式(7)(23)，可以建立获得MIMU/GPS组合导航的量测方程为

其中，H为量测矩阵，V为量测白噪声。从而，获得组合导航系统的状态方程和量测方程。由于量测方程本身即是离散的，因此只需对连续的系统状态方程进行离散化处理，就可以采用卡尔曼滤波方程进行滤波计算了，进而获得系统状态（即系统误差）的实时估计值。此时，利用该估计值实时对MIMU导航解算结果进行误差校正，并将校正后MIMU输出的导航参数作为组合导航系统的输出。

4 实验验证

对文中所研究的组合导航方法分别进行计算机仿真验证与实际系统离线验证。首先进行仿真验证，设MIMU中陀螺仪常值漂移为20 (°)/h，随机游走为加速度计的常值偏置为10-3g，随机游走为设GPS伪距噪声的均方差为3 m，伪距率的噪声均方差为0.05 m/s，伪航向角的噪声均方差考虑为20′；设MIMU导航解算的初始水平姿态误差为2°，初始方位误差为5°，初始位置误差为10 m，初始速度误差为0.1 m/s。MIMU输出频率为200 Hz，GPS输出频率为1Hz，滤波周期为1s，组合导航仿真时间为600 s。

为了充分验证文中算法的性能，对有、无航向信息辅助的MIMU/GPS组合导航分别进行了仿真，仿真结果如图2～3所示。其中，“粗实线”为有航向信息辅助的MIMU/GPS组合导航仿真结果，“细虚线”为无航向信息辅助的仿真结果。

根据图2～3可以看出，尽管采用了低精度的微惯性器件，文中研究的组合导航方法仍具有较高的精度：在600 s的仿真时间内，水平位置精度达到±8.3 m(3σ)，高度精度达到±10.1 m(3σ)，航向精度达到±18.7′(3σ)，水平姿态精度达到±20.3′(3σ)。可见，引入航向信息辅助后，组合导航的航向精度与水平姿态精度基本相当，没有出现航向精度较低甚至发散的情况。相比之下，在无航向信息辅助的情况下，航向误差最大达146.8′，而且有明显的发散趋势，至于其位置精度与水平姿态精度则与有航向信息辅助的情况基本相当。同时，根据仿真结果也可看出，尽管MIMU导航的初始姿态误差较大（水平姿态误差为 2°，方位误差为 5°），但组合导航的姿态误差仍然快速收敛，而且能够稳定控制在较高的精度范围内。这就说明文中所研究的组合导航方法能够适用于失准角较大的情况。

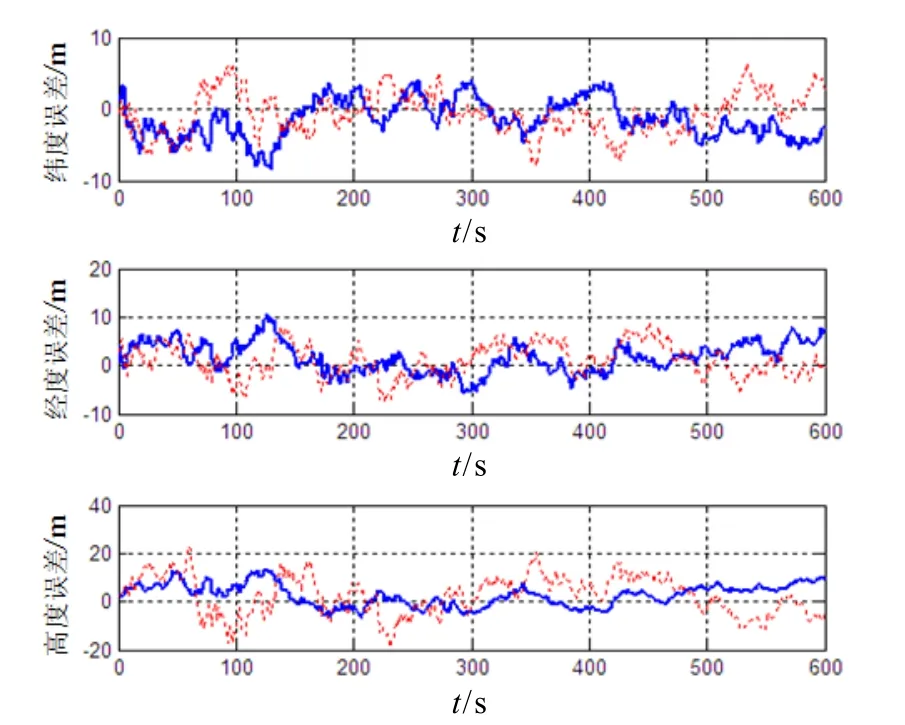
图2 组合导航仿真的位置误差Fig.2 Position errors of integrated navigation simulation

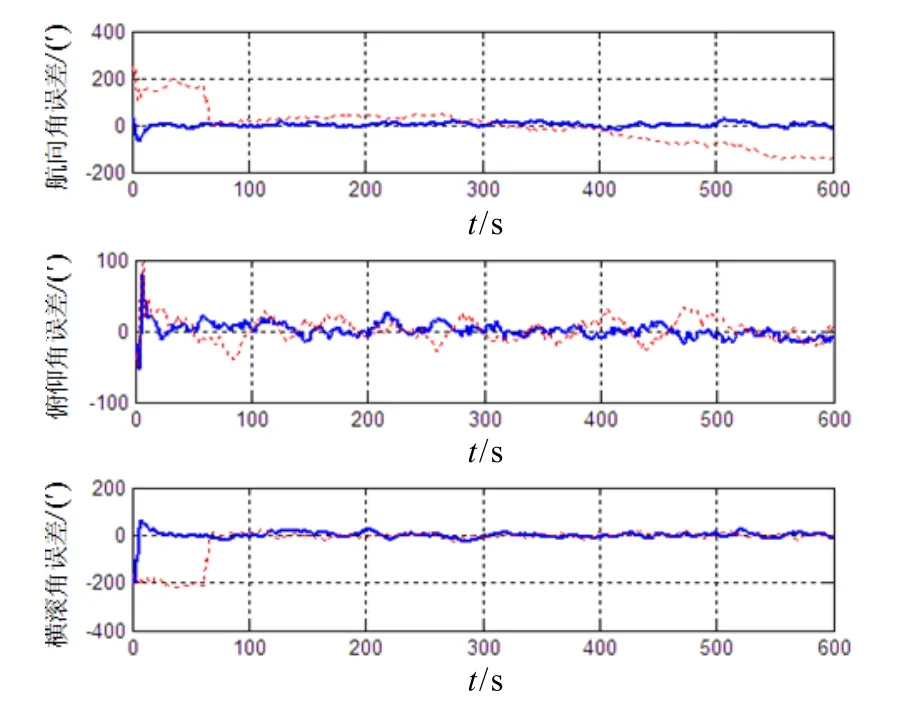
图3 MIMU/GPS组合导航仿真的姿态误差Fig.3 Attitude errors of MIMU/GPS integrated navigation simulation

利用实验室现有的中等精度微惯组（陀螺常值漂移约10 (°)/h，加速度计常值偏置约10-3g）与GPS接收机在高速公路上开展 MIMU/GPS组合导航跑车试验，试验车与主要设备如图4所示。为了考核MIMU/GPS组合导航的姿态精度，车上搭载双天线GPS定姿系统，其基线长5 m，定姿精度约为3′。

图4 组合导航试验车Fig.4 Test vehicle of integrated navigation

跑车过程中实时采集并存储MIMU和GPS的实际输出数据，以及双天线GPS定姿的输出数据。事后利用采集的实际数据，对有、无航向信息辅助的MIMU/GPS组合导航分别进行了离线验证。其中，为了检验文中算法对于 GPS卫星颗数少于四颗时的组合导航效果，在导航过程中人为作以下设置：1）第240～300 s，仅收到3颗卫星的信号；2）第560～620 s，仅收到2颗卫星的信号；3）第900～960 s，仅收到3颗卫星的信号；在上述三个时间段内不利用GPS伪航向角来辅助组合导航。验证结果如图5～6所示，其中“粗实线”为有航向信息辅助的离线验证结果，“细虚线”则为无航向信息辅助的验证结果。

图5 组合导航跑车验证的位置误差Fig.5 Position errors of integrated navigation test by vehicle

图6 组合导航跑车验证的姿态误差Fig.6 Attitude errors of integrated navigation test by vehicle

根据图5～6可以看出，MIMU/GPS组合导航跑车试验结果与前面仿真验证结果一致：航向信息辅助下的位置精度、水平姿态精度与无航向信息辅助的精度基本相当；而有航向信息辅助时的组合导航航向精度则依然远远高于无航向信息辅助时的精度。因此，实际系统跑车试验再次证明引入航向信息辅助对于解决组合导航航向精度较低甚至发散问题的有效性。同时也可看出，尽管导航过程中多次出现有效卫星颗数少于四颗的情况，但是在航向信息辅助下 MIMU/GPS组合导航系统仍保持较高精度：位置精度控制在±10.3 m(3σ)，航向精度控制在±19.5′(3σ)，水平姿态精度控制在±20.1′(3σ)。这就说明伪距组合模式能够有效应对卫星颗数少于四颗而无法定位的问题。但也可以看出，当卫星颗数少于四颗时对组合导航效果还是造成了一定影响，主要体现在位置误差和姿态误差出现小幅跳动，不过仍能满足一定精度的导航要求。

5 结 论

综上所述，本文研究了基于航向信息辅助的MIMU/GPS高精度组合导航方法，通过构造等效伪距，将其与 GPS输出伪距相减作为组合导航量测之一；以车辆、导弹、火箭弹等载体为应用背景，利用GPS速度输出计算获得伪航向角，将MIMU导航解算获得的航向角与该伪航向角相减作为量测之二；采用卡尔曼滤波设计组合导航滤波算法。该组合导航方法具有精度高、可靠性好、计算量适中等优点，即便在卫星颗数少于四颗时仍能保持较高精度，而且在失准角较大的情况下也能够实现滤波的快速收敛。因此，具有良好的理论研究与工程应用价值。