不同分布下Realized EGARCH模型的拟合效果研究

玄海燕，戴天骄，李鸿渐，郭长青

（兰州理工大学 经济管理学院，兰州 730050）

0 引言

如何合理地拟合波动率在金融领域一直是研究的重点。在金融时间序列的条件异方差模型拟合方面，以Engle(1982)[1]提出的自回归条件异方差(ARCH)模型和Bollerslev(1986)[2]提出的广义自回归条件异方差(GARCH)模型为主，这也是最早且得到广泛应用的条件异方差模型。

GARCH类模型存在的主要问题是研究样本只能为低频数据（在证券市场中主要为日数据），而信息化技术的进步增强了数据采集能力，高频数据越来越多的在应用研究中出现，向主要在低频数据层面应用的GARCH类模型提出了新的需求。高频数据的不规则交易间隔、离散取值、强自相关性、日内模式的特征让传统的计量模型在实际应用中表现不佳，因此学者们开始研究用于高频数据层面的GARCH类相关模型。Andersen等(2008)[3]提出专用于高频数据的“已实现测度”。此后将已实现测度和传统的GARCH模型结合用于高频数据的波动率建模成为了一个研究热点。最初，研究主要集中在GARCH-X模型上，这类模型直接将已实现测度作为外生变量纳入，模型形式较为简单，但是在预测方面存在缺陷。因此，建立把波动率和已实现测度联合、具有优良预测能力的模型成了后续的研究方向。Hansen等(2012)[4]提出的Realized GARCH模型就是其中之一，在传统的GARCH模型中加了已实现测度，并利用已实现测度的方程（测量方程）将条件方差和已实现测度联系起来。王天一和黄卓(2012)[5]将Realized GARCH模型推广到厚尾分布的情形，认为Skewed-t分布可以较好的反映收益率的尖峰厚尾的特征，同时使用t分布的预测精度最高。黄雯等(2012)[6]认为基于Skewed-t分布Realized GARCH模型拟合情况和尾部风险描述能力明显优于正态分布和t分布下的Realized GARCH模型。王天一等(2014)[7]使用多种频率的已实现波动率及实现核估计作为已实现测度进行分析，采用t分布和正态分布并和GARCH、EGARCH模型进行对比，认为数据频率、分布设定以及不同已实现测度对其预测能力有影响。魏正元等(2015)[8]研究认为误差项服从Skewed-t分布的Realized GARCH(1,2)模型对于上证380的拟合能力较好，并且能够精确地测量其收益风险。Hansen和Huang(2012)[9]基于Realized GARCH模型进行拓展，提出了Realized EGARCH模型，对Realized GARCH模型中的GARCH方程进行修改，使得Realized EGARCH模型能够更好地反映当前市场上存在的非对称性特征。Banulescu等（2016）[10]将Realized EGARCH模型进一步推广，考虑了robust结构的杠杆函数并与Realize GARCH模型对比。

Hansen和Huang(2012)[9]对于Realized EGARCH模型的研究主要基于正态分布，对于t分布及Skewed-t分布下的模型情况并没有进行研究。因此，本文针对上证指数的5分钟高频数据，探讨基于t分布及Skewed-t分布下Realized EGARCH模型的拟合情况，并与正态分布下的拟合情况进行对比。结果表明，基于t分布及Skewed-t分布下Realized EGARCH模型的拟合效果明显优于正态分布下的情况，但是二者之间差异不大。

1 模型简介

1.1 模型形式

Hansen和Huang(2012)[9]提出的Realized EGARCH模型如下所示：这三个式子中，式（1）被称作是回归方程，式（2）是GARCH方程，式（3）则被称为测量方程。其中μ通常设定为0，但是会根据数据出现拟合结果不为0的情况。zt、ut独立同分布且 zt～iid(0，1) ，ut～iid(0，) ，ut=u1，t，u2，t，…，uK，t，k=1，2，…，K ，xt是由高频数据计算出的已实现测度。GARCH方程和测量方程中的杠杆函数的形式如下所示：

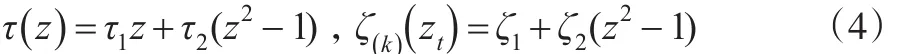
这两个杠杆函数在整个模型中起着相当重要的作用，通常扮演着在现实中使zt、ut具有独立性的因素的角色，同对回归冲击和波动率冲击的非独立性关系建模，波动率冲击由 νt=τ(zt-1)+γut-1得出，其绘图后即为 Realized GARCH模型的信息冲击曲线，形式为νt=E(loght+1|Ft)-E(loght+1|Ft-1)。

Realized EGARCH模型中的三个方程与Hansen等(2012)提出的Realized GARCH模型中的三个方程有所区别。Realized GARCH模型的前两个方程的基于GARCH-X模型，采用了与Engle(2002)、Barndorff-Nielsen和Shephard(2007)、Visser(2011)相似的形式，而测量方程则是Realized GARCH框架相比于其他模型的特色所在，加入了杠杆函数来描述波动率对于收益率冲击的非对称反应。两个模型的差异主要体现在GARCH方程上，Realized EGARCH模型并没有将logxt直接纳入计算，而是替换为一个杠杆函数logxt方程中ut的滞后项的和的形式。因此τ(zt-1)+γut-1被称为条件波动率的创新。

1.2 已实现测度选择

测度方程中可以使用的已实现测度种类较为丰富，较为常用的有以下四种：已实现波动率(realized variance,RV)，已实现核估计(realized kernel,RK)，已实现二次幂变差(realized bipower variation,RBV)，已实现极差(realized range,RR)。已实现波动率是通过计算日内收益率的平方和来估计波动率，并且是积分波动IR的一致估计量。因而虽然后续提出了诸多已实现测度，但已实现波动率仍然是其中应用较为广泛的一种。在这里本文使用RV作为测量方程中的xt。已实现波动率的表达式如下：

其中m为一天的样本数，i为第t天的第i个样本。m的值取决于采样频率，频率越高，每日数据量越大。这里采用5分钟高频数据，所以本文取m=48。由于市场微观噪声的存在，采样频率过高会使RV值严重偏离，过低则信息量有损失，因此必须寻找最优的采样频率。

1.3 似然函数

Realized EGARCH模型的似然函数由两部分组成：

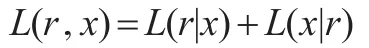
其中，L(r|x)+L(x|r)为似然函数中对应ut和zt的部分，在进行模型间分布拟合和预测能力的比较前必须确保使用相同的数据，但是由于在与不同模型比较时L(x|r)不一定都存在，因此只使用似然函数中L(r|x)的部分，即半似然函数。试用半似然函数值进行比较的方式在王天一等、黄雯等的研究中均有试用。由于本文进行的对比研究是基于相同模型，单独计算L(r|x)要更加麻烦，为简化计算，直接使用L(r，x)进行比较，形式如下：

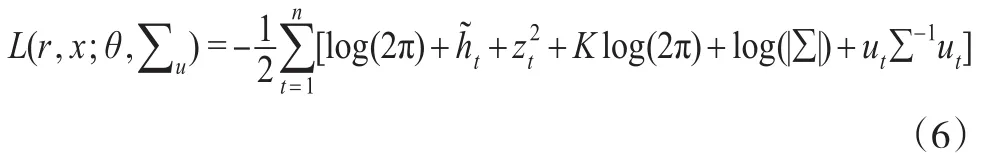
1.4 分布形式

本文采用的t分布为Bollerslev(1987)提出的标准化t分布，形式为：

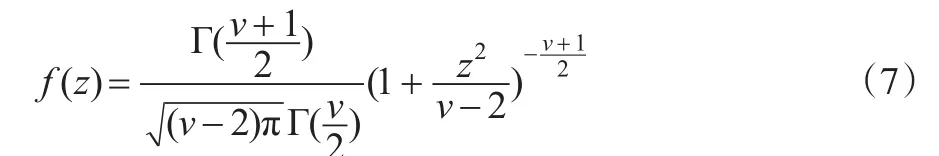
Hansen(1994)提出的Skewed-t形式为：

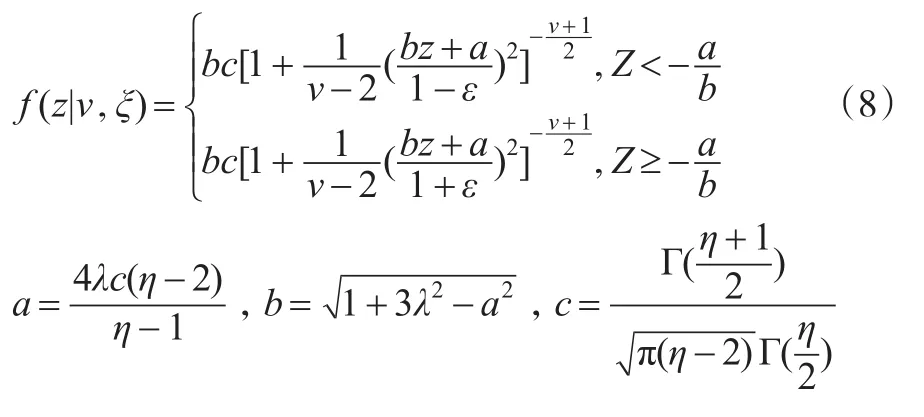
其中ν为自由度，ε体现了分布函数的偏斜情况，当ε＞0时，分布右偏；当ε＜0时，分布左偏；ε=0时，整个分布退化为标准化t分布。

虽然从分布的特征上来说，Skewed-t分布比t分布更能体现金融时间序列尖峰厚尾、有偏的性质，在对Realized GARCH模型分布拟合的相关研究中被认为Skewed-t分布的拟合效果明显优于其他分布，但是Realized EGARCH模型的结构与Realized GARCH模型的结构相比，更加强调了杠杆函数的部分，对于不对称性的反应相比Realized GARCH模型来说已经有了增强。与t分布相比Skewed-t分布也只是多考虑了偏度的影响，因此不确定基于Skewed-t分布的拟合结果一定优于t分布下的拟合结果。由于目前还没有相关文献证明基于t分布下的Realized EGARCH模型已经足够反应金融时间序列本身的特征，因此基于多种分布对于Realized EGARCH模型的拟合情况的影响进行研究是有必要的。

2 实证分析

2.1 数据统计特征及模型参数估计

本文使用的数据为2016年1月8日到2017年3月24日共294个交易日的5分钟高频数据，每日交易时间为4小时，共48个数据点。收益率采用“收盘价—收盘价”的形式计算。对数收益率的表达式为：

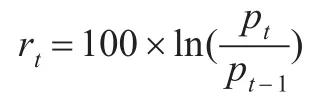
其中pt为当前时刻收盘价，pt-1为前一时刻收盘价。5分钟收益率序列和已实现波动率序列如图1所示。可以看出这两个序列都存在明显的波动率集聚现象。而且由于数据选择区间包括了极端区间，数据左侧波动十分剧烈。

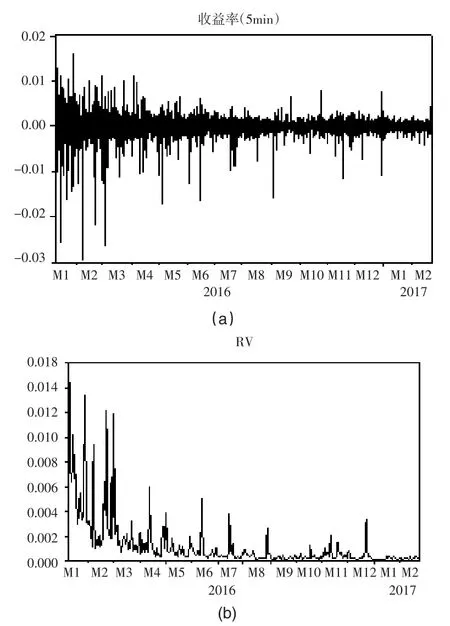
图1 上证指数收益率序列及已实现波动率序列

表1计算了两个序列的基本统计量。从中可以看出收益率序列rt与对数已实现波动率RV5存在着显著的尖峰特征。在正态性检验上采用了K-S检验，Z值分别为14.360和7.610，括号内为p值，p值＜0.05，显著地拒绝了正态分布假设。从偏度来看，rt与logRV5序列的偏度都在0附近，说明数据偏斜不强，这可能会对Skewed-t分布下的拟合效果产生一定的影响。因此从描述性统计的结果来说，t分布可能与Skewed-t分布的拟合情况相似。

表1 描述性统计

使用上述数据进行模型参数估计结果如表2所示。其中，RE为Realized EGARCH模型的简写，N为正态分布，t为t分布，S-t为Skewed-t分布。括号内为参数的标准误差（std.error）。估计方式为QMLE（Quasi-maximum Likelihood Estimate），即准极大似然估计。

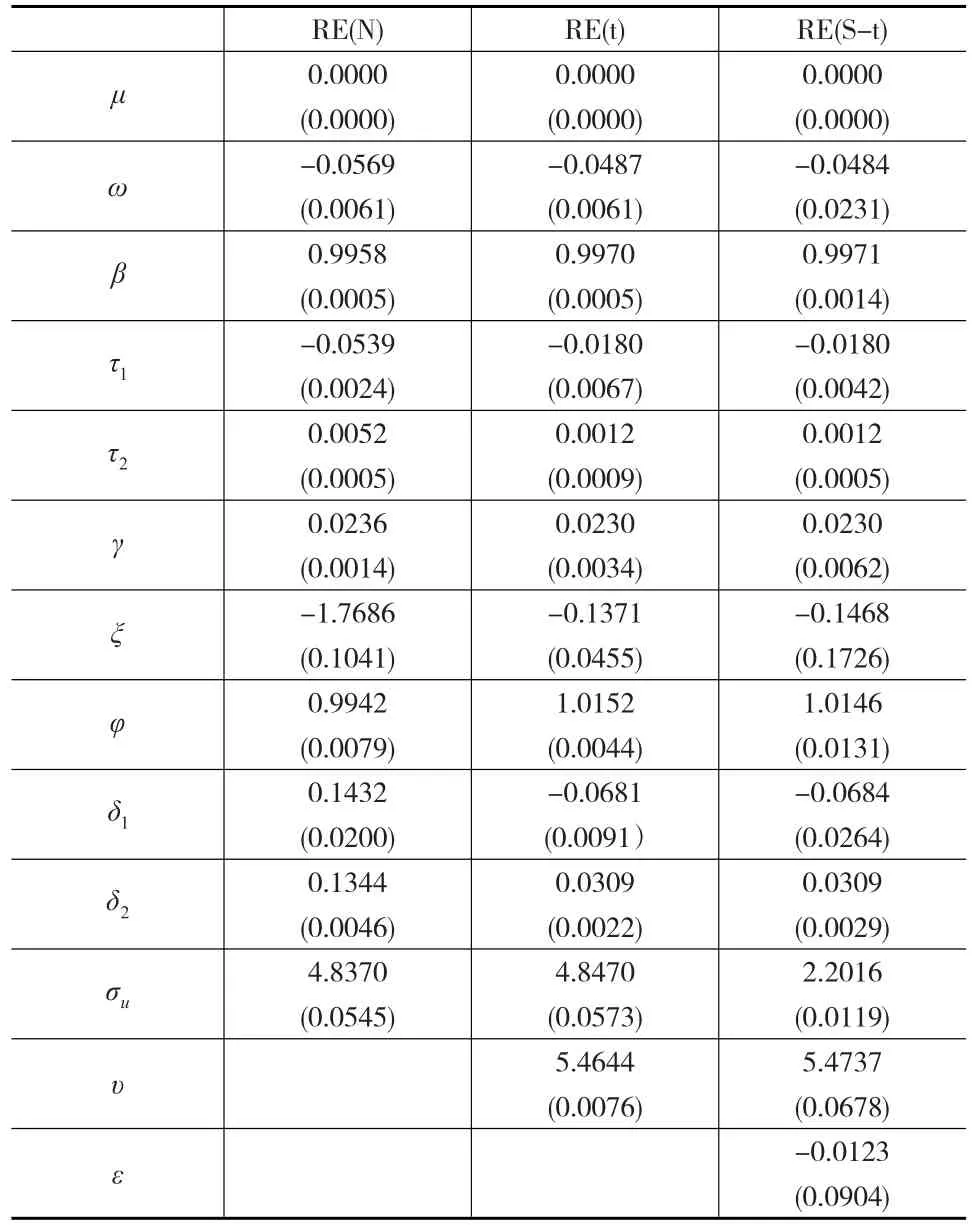
表2 Realized EGARCH模型的参数估计

从参数估计结果来看，由于ε＜0，说明残差分布存在一定的偏斜，且为左偏，但是偏斜较为微弱，这可能是由于RV5和rt序列的偏度不强的结果。三种分布下估计出的τ1、τ2和δ1、δ2的值均为一负一正，体现出了模型的非对称性，并且t分布和Skewed-t分布下杠杆函数的参数τ1、τ2和δ1、δ2的值基本相同，说明二者在对数据非对称性的反应上基本相同。从标准误差来看，正态分布下参数的标准误差、t分布下的参数标准误差和Skewed-t分布下的标准误差各有大小，无法从参数估计的标准误差上来准确评定模型的参数拟合情况。但是从参数估计的结果来看，t分布下的参数估计结果应当是最优的，这种最优可能与模型选择的已实现测度的种类、数据的时间区间有关，如果偏度相反或者都接近0，则使用t分布要更为简单。

图2为三种分布情况下Realized EGARCH模型的信息冲击曲线。可以看出t分布和Skewed-t分布下的信息冲击曲线比正态分布的曲线形状更加分明，且对称轴偏离0较多，说明这两种分布体现了更强的不对称性，更能够体现Realized EGARCH模型的强非对称性的性质。

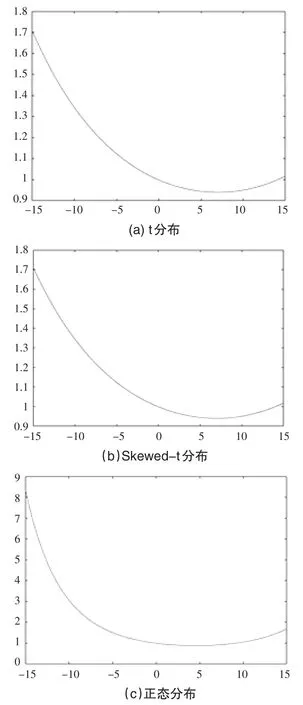
图2 信息冲击曲线

2.2 分布拟合能力评估

对于模型的拟合能力进行评估时，使用似然函数进行比较。表3中logL（Log likelihood function）为对数似然函数值，其数值越大说明在相应参数下获得所用数据的可能性越高。

表3 三种分布的拟合能力评估指标

从对数似然函数的值来看，仍然是Skewed-t分布下的拟合结果的对数似然函数值最大，但与t分布下的拟合结果差异不大。正态分布下拟合结果的对数似然函数值最小，与其他两个分布相比显得拟合结果不够优良。

3 结论

本文主要研究基于高频数据的波动率模型——Realized EGARCH模型在残差服从三种不同分布下时模型的拟合情况，并使用上证指数进行了实证研究。上证指数的收益率明显地表现出尖峰厚尾、有偏的特征，这也是金融时间序列数据的所特有的。Realized EGARCH模型与Realized GARCH模型相比，在模型形式上加强了对非对称性的反映，其结构本身可以产生一定的峰度和偏度，但是这种偏度和峰度仍然不足以拟合数据，在正态分布下拟合上证指数数据产生的较大的标准误差可以说明这一点。

另外，不同的已实现测度可能对模型结果会产生不同的影响，本文只使用已实现波动率作为已实现测度，诸多相关研究表明已实现波动率相比其他已实现测度可能存在一定的误差，进而影响模型的拟合情况，这是下一步研究的范畴。

最后，在对于上证指数数据的残差服从正态分布、t分布、Skewed-t分布下Realized EGARCH模型进行的拟合研究结果表明，这三种分布中的Skewed-t分布在拟合模型时具有较为良好的性质，但是其拟合效果与t分布的拟合效果差异不大，这可能与数据的选择及已实现测度的选择有关。总体来说，对上证指数使用以上三种不同的分布进行Realized EGARCH模型的拟合时，Skewed-t分布的拟合效果最好。