一种同步组网跳频信号的盲分离方法
2018-12-19
(南昌理工学院 电子与信息学院,南昌 330044)
1 引 言
同步组网跳频电台信号分离是跳频信号盲分离的一个难点。由于同步组网跳频电台中不同电台的跳频周期、跳变时刻、跳频频率集完全相同[1],这就使得利用上述跳频信号参数对各电台信号进行盲分离不再可行。文献[2]指出对于同步组网跳频电台,各电台之间的差异主要体现在三个方面:一是建网过程存在差异,即不同电台在捕获同步信息时所使用的频率有差异;二是网络信息参数存在差异,即网号和相关码不同;三是信号到达角度(Direction of Arrival,DOA)存在差异。考虑到盲源分离问题主要集中在解决各电台已经完成同步之后的分离算法,以及提取网号和相关码解跳难度较大的情况,尚没有文献依据建网过程差异和网络信息参数差异对跳频信号盲分离进行研究。文献[3-4]提出基于空时频分析的跳频信号DOA估计,并利用聚类算法对同步组网跳频电台信号进行分离。但这只利用到了方向信息,且空时频分析的难度本身就比较大,其对测向精度要求也比较高,从而限制了这些理论的进一步发展。由于跳频信号在时频域上具有稀疏性,时频分析方法被广泛应用于跳频信号处理中[5-6]。文献[7]提出了基于短时傅里叶变换(Short Time Fourier Transform,STFT)时频比的盲信号分离算法。文献[8]运用多种时频分析手段,在时频域上对异步组网混合跳频信号进行分离。文献[9]将图像处理方法引入时频分析,对跳频信号参数进行估计。但这些方法没能解决信号特征的估计与提取问题,在跳频频率间隔较小、电台较多时无法达到预期的分离效果。另一方面,独立成分分析[10-12](Independent Component Analysis,ICA)是盲源分离的一个重要工具,也可以应用于跳频信号的分离中:文献[13]证明了跳频信号盲分离问题满足ICA算法的求解条件;文献[14]将FastICA算法应用于跳频信号的盲分离,通过计算源信号与分离信号的相关系数来衡量分离算法的有效性,证明了算法的可行性。ICA的一个缺点是分离后的信号顺序、幅度、相位相对于源信号都会有所改变,而且计算量比较大,这使得它的应用在一些特定条件下受到限制。
本文在采用平滑伪魏格纳分布(Smoothed-pseudo Wigner-Ville Distribution,SPWVD)对同步组网跳频信号进行特征提取的基础上,充分利用同步组网跳频电台信号的特点,应用STFT时频比的方法对同步组网跳频信号进行分离,并且在跳频信号间隔较小的条件下完善了分离算法。
2 信号模型
输出的可观测信号X(t)是含噪声N(t)的源信号S(t)的瞬时线性混合。X(t)满足下列方程:
X(t)=AS(t)+N(t)。
(1)
式中:A为M×N的混合矩阵(M≥N),M表示多天线接收系统中接收通道数量,N表示跳频信号源的数目。
基于以上模型的跳频信号盲分离问题可以描述为:在混合矩阵A和原信号矢量S(t)均未知的条件下,求一个N×M的分离矩阵W,使得W对混合信号矢量X(t)的线性变换Y(t)为对源信号矢量S(t)的一个可靠估计:
Y(t)=WX(t)=WAS(t)。
(2)
3 基于SPWVD分布的跳频信号特征提取
3.1 SPWVD分布原理
魏格纳分布(Wigner-Ville Distribution,WVD)分布是Cohen类时频分布的一种,相比于STFT变换,其时频聚集性更好。信号x(t)的WVD分布定义如下:
(3)
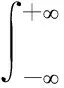
WVD分布有其自身的缺点,它对多分量信号或者频谱非线性变化的单分量信号(如跳频信号)的时频分布存在严重的交叉项干扰[10]。为了降低和消除WVD带来的交叉干扰,常对WVD结果在时域和频域进行平滑,以取得更好的效果。在这些平滑的方法中,SPWVD的效果较好:
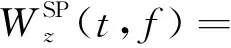
z*(t-μ-τ/2)ej2πftdμdτ。
(4)
式中:h(t)和g(t)是奇数长度的窗函数,满足h(0)=G(0)=1,G(f)表示g(t)的傅里叶变换,信号z是信号x的解析形式。
尽管SPWVD对交叉项干扰有一定的控制作用,但当跳频信号频率间隔较小且网台数目较多时交叉项仍然会大量存在,这给参数估计带来了很大的困难。
3.2 基于二次差分和时频分布距离检测的同步组网跳频信号特征提取
提取特征参数是实现混合跳频信号分离的前提。同步组网跳频信号具有跳时相同、跳周期相同的特性给SPWVD估计跳频时刻带来了便利。在估计出每一跳的中心时刻后,对相邻跳频中心时刻进行差分,去除误差后即可得到跳频周期的估计。在限定了跳时和跳周期的基础上,便可以进一步提取跳频信号的特征。
本文通过二次差分的方法估计混合跳频信号的跳时。首先,在SPWVD的频率方向求极值。
对于跳频信号时频分布中,任意频率方向上的列向量构成的实序列x(n),n=1,2,…,N,一次差分的结果记为
(5)
二次差分的结果记为
(6)
在新得到的序列diff2(n)中,只存在0和1两种取值,将取值为1的时频点称为序列x(n)的峰值。为了增加估计的精度,对多路信号作相同的处理,将多路信号的峰值时频分布叠加,求出二次差分结果得到的峰值位置的均值,得到修正的SPWVD峰值分布,记为SPP(i,j)。
虽然SPWVD有较好的交叉项抑制性能,但在信号数量较大时,在时频分布平面上距离较近的信号间依旧会存在交叉项干扰。故本文采用检测最大值点在时频分布平面距离的方法求解跳频信号每一跳的中心时刻,再根据中心时刻和跳频周期提取待分离信号的特征,具体方法如下:
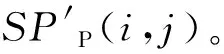
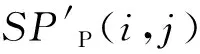
Step3 将SPPM(i,j)在时间轴上投影,并进行简单聚类。聚类的目的是消除存在于同一跳频周期内不同频点峰值时刻的细微偏差造成的干扰。求出聚类中心,并将原值舍去,聚类中心即为各跳的中心时刻,记为T(n),对T(n)做一次差分,方法同公式(5),即可得到跳频周期估计序列diffT(n),n=1,2,…,N。由于观测时间内第一跳与最后一跳可能不足一个跳频周期,故将这两个点舍去。则同步组网信号的跳频周期估计为
(7)
Step4 在时频分布SPP(i,j)平面内提取信号特征。该特征表达为:在特征区域内,只包含单个跳频信号某一跳的信息,而不被其他信号干扰。设各跳的中心时刻为Tc(n),2≤n≤N-1,对应各跳的中心频率为Fc(m),2≤m≤M(N-1)(M表示跳频信号数目)则在时频分布平面上提取的信号特征表示为
(8)
式中:σf为单个SPWVD在频率方向的估计误差。
4 基于时频比方法的跳频信号盲分离
由于跳频信号等效窄带信噪比较高,忽略噪声的情况下,信号模型近似为
X(t)=AS(t)。
(9)
将式(9)展开,则有
(10)
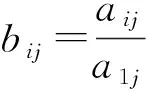
S′(t)=B-1X(t)。
(11)
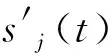
(12)
假设在时刻tm,源信号sj(tm)≠0且其他si(tm)=0,i≠j,则有
(13)
对于混合的同步组网跳频信号来说,在时域中,没有满足上述条件的tm。但是在时频域里,由于跳频信号的频点分布分散,依据第2节中信号特征提取方法,可确定Chop(i,j),使其只包含一个源信号。但是,WVD类时频分布是非线性的,变换后的时频比不能作为bij的估计,故要对接收信号进行线性的STFT变换。下面对STFT变换后信号是否满足求解条件进行简要分析。
对xi(t)作STFT变换,假设在时频窗Chop(i,j)内,Sj≠0而其他Si=0,则有
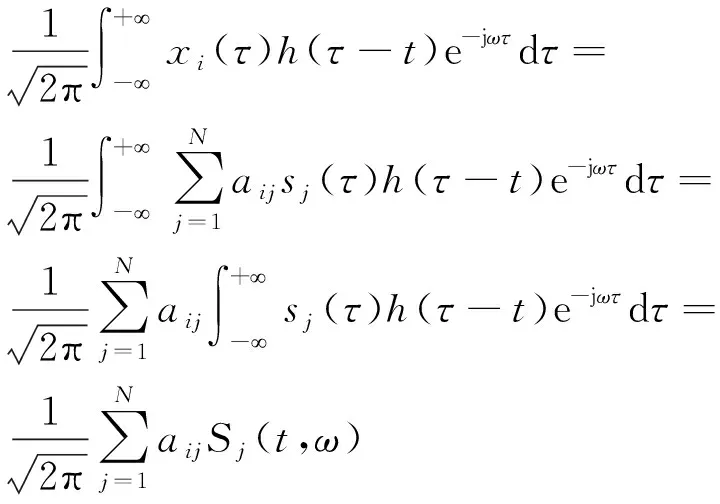
(14)
假设在时频窗(tp,ωk)内,Sj(tp,ωk)≠0而其他Si(tp,ωk)=0,则有
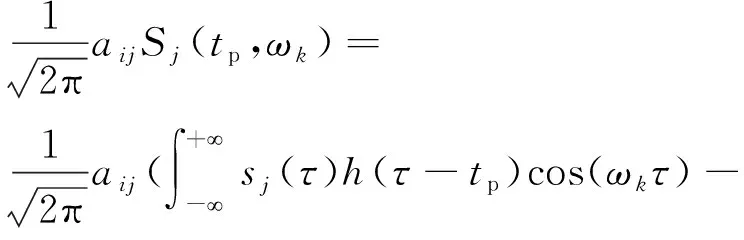

Xireal(tp,ωk)+jXiimag(tp,ωk)。
(15)
如式(15)所示,STFT是线性变换,满足叠加定理。只要在对各路信号取相同的时间窗,就可保证式(13)中的比值不变性,从而求出bij:
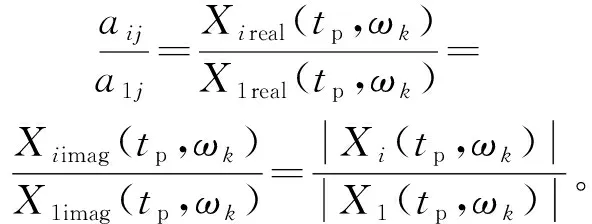
(16)
由于STFT变换在频率分辨率与时间分辨率上存在矛盾,若时间窗长度太短,会导致频率分辨率降低。所以为了保证估计效果,可以将提取的信号特征区域扩展后,再进行STFT变换。即在通过SPWVD变换提取信号特征后,在时域上将信号扩展为
(17)
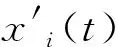
5 仿真实验与结果分析
为了验证上面的算法,不失一般性,本文采用m序列驱动下的跳频信号进行仿真,跳频周期为500 μs,采样率满足Nyquist采样定理,每跳对应32个采样点,采样点数满足时频信号分析需求。仿真中,采样点对应的时间长度为8跳。本文设置了两路源信号与两路接收信号,混合矩阵A服从(0,1)间均匀分布,其余仿真参数见表1。

表1 跳频信号仿真条件Tab.1 Simulation parameter of FH signals
仿真得到2个源信号如图1所示。
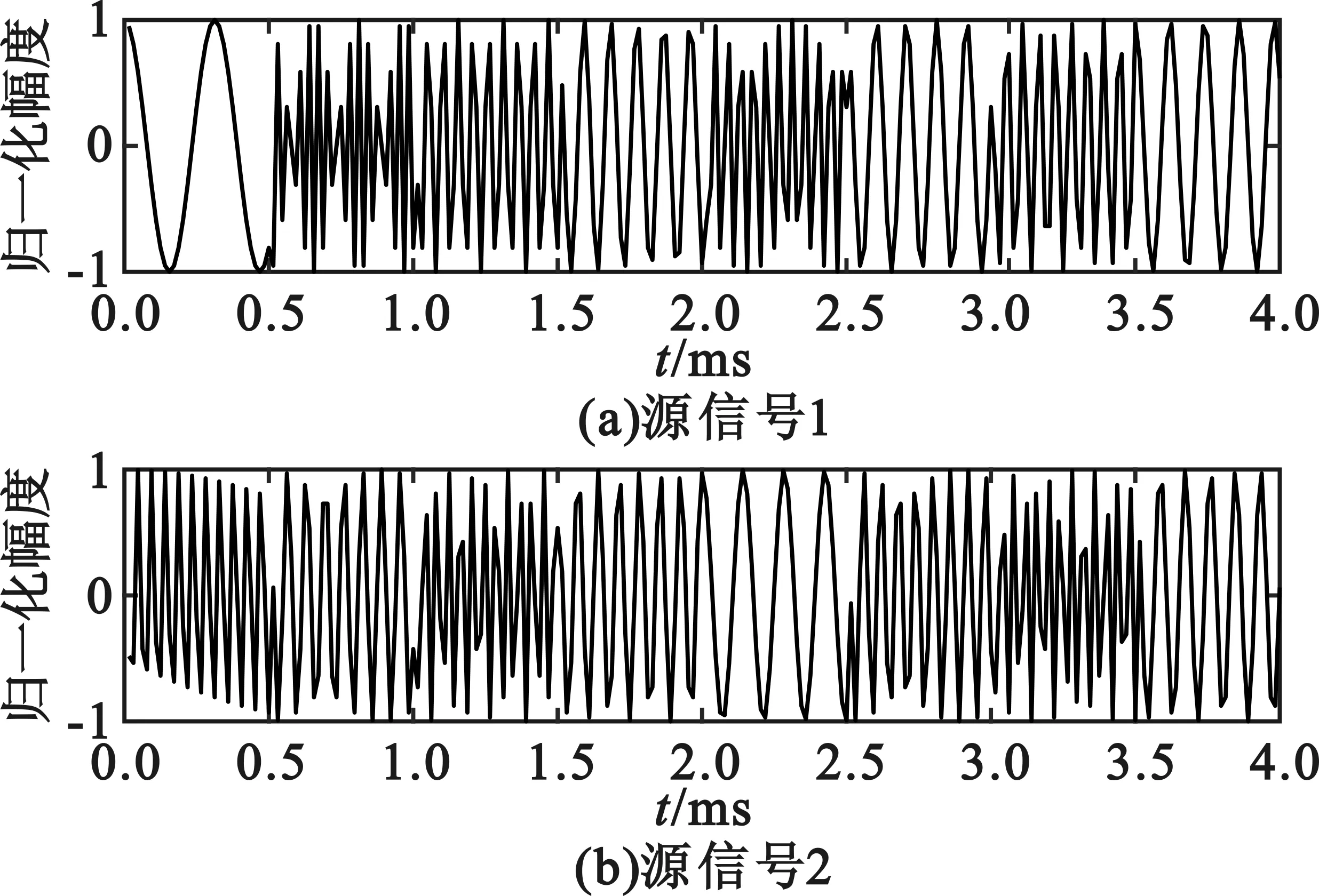
图1 源信号的时域表示Fig.1 Source signals in time-domain
随机产生混合矩阵:

在各路信号信噪比均为10 dB的条件下,使源信号通过混合矩阵,得到的接收信号如图2所示。
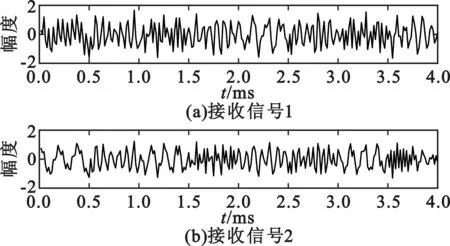
图2 接收信号的时域表示Fig.2 Received signals in time-domain
对接收信号进行SPWVD分析,并提取信号特征。图3与图4分别表示经过SPWVD变换的两路接收信号,其受到了一定的交叉项影响。
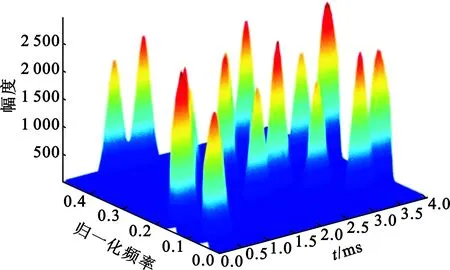
(a)3维
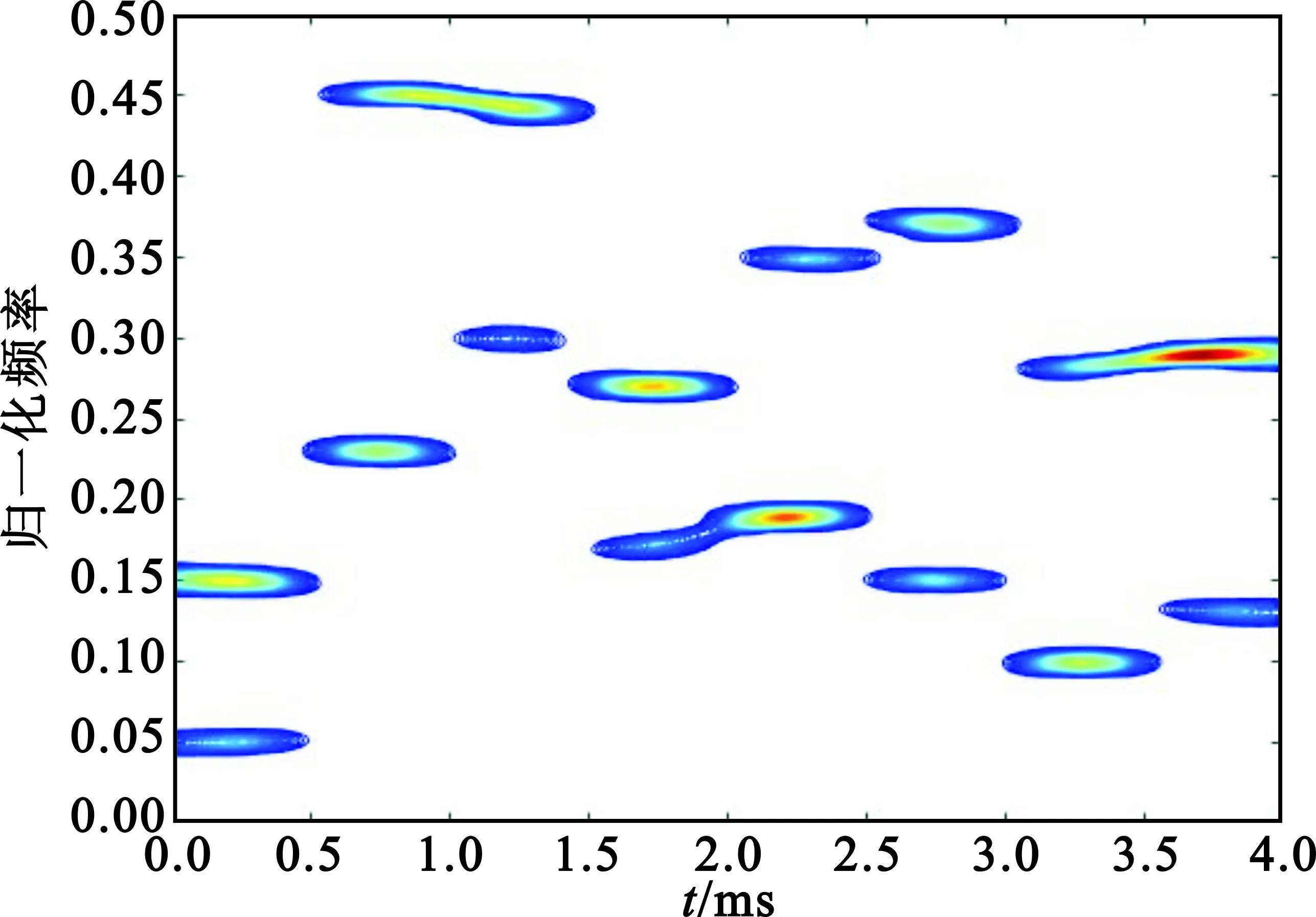
(b)2维图3 接收信号1的SPWVD分布Fig.3 SPWVD of received signal 1
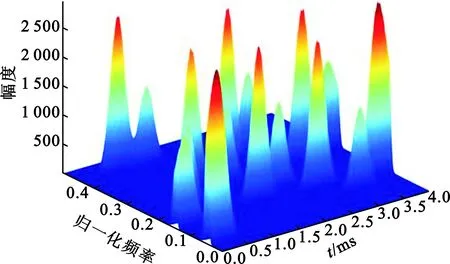
(a)3维
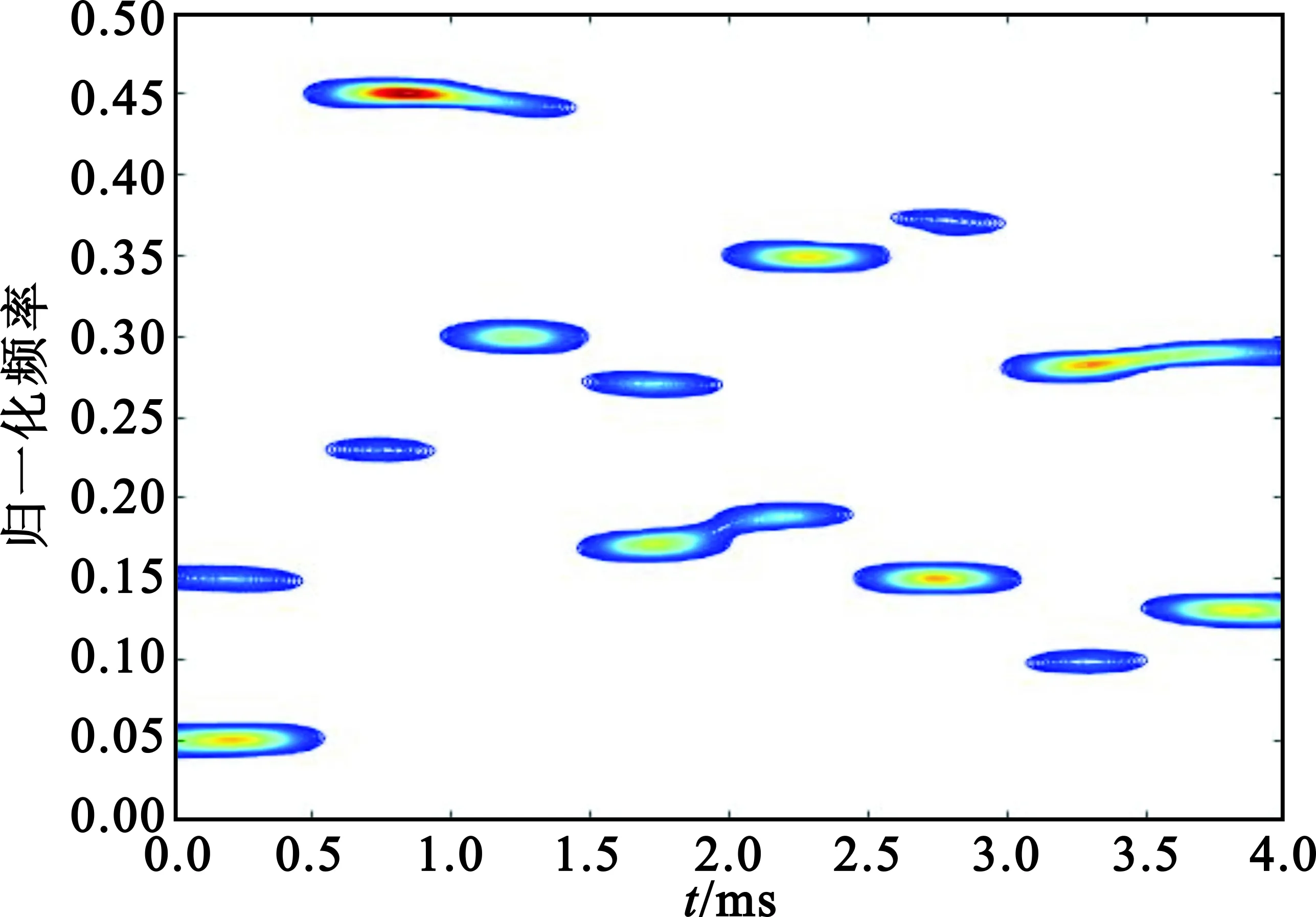
(b)2维图4 接收信号2的SPWVD分布Fig.4 SPWVD of received signal 2
经过二次差分提取频率方向峰值(如图5所示)之后,同步跳频信号的峰值的时频分布仍能比较清晰地反映出跳频信号的规律。图6所示为最终的跳频信号特征提取结果。
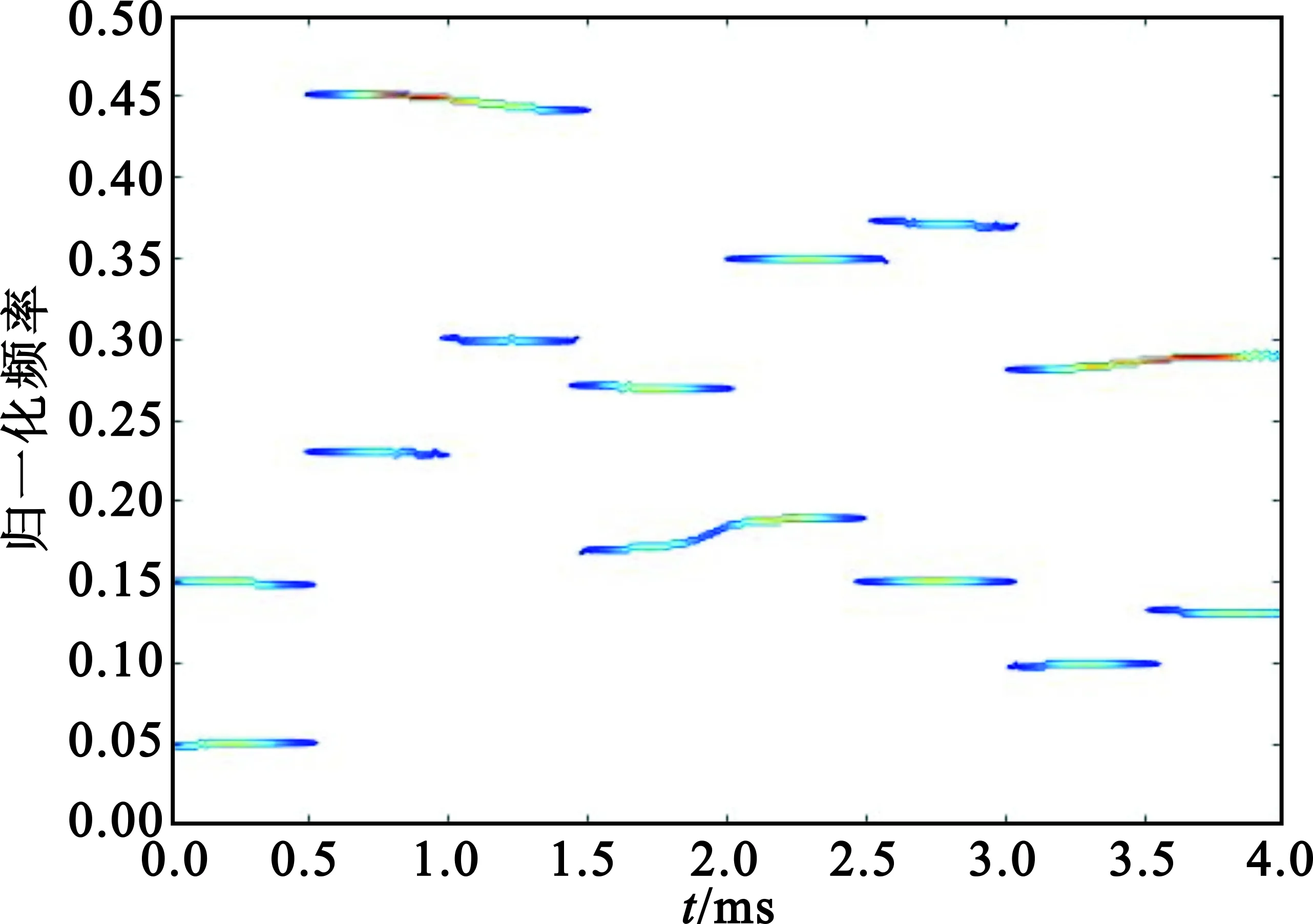
图5 频率方向峰值的时频分布Fig.5 Peaks in frequency
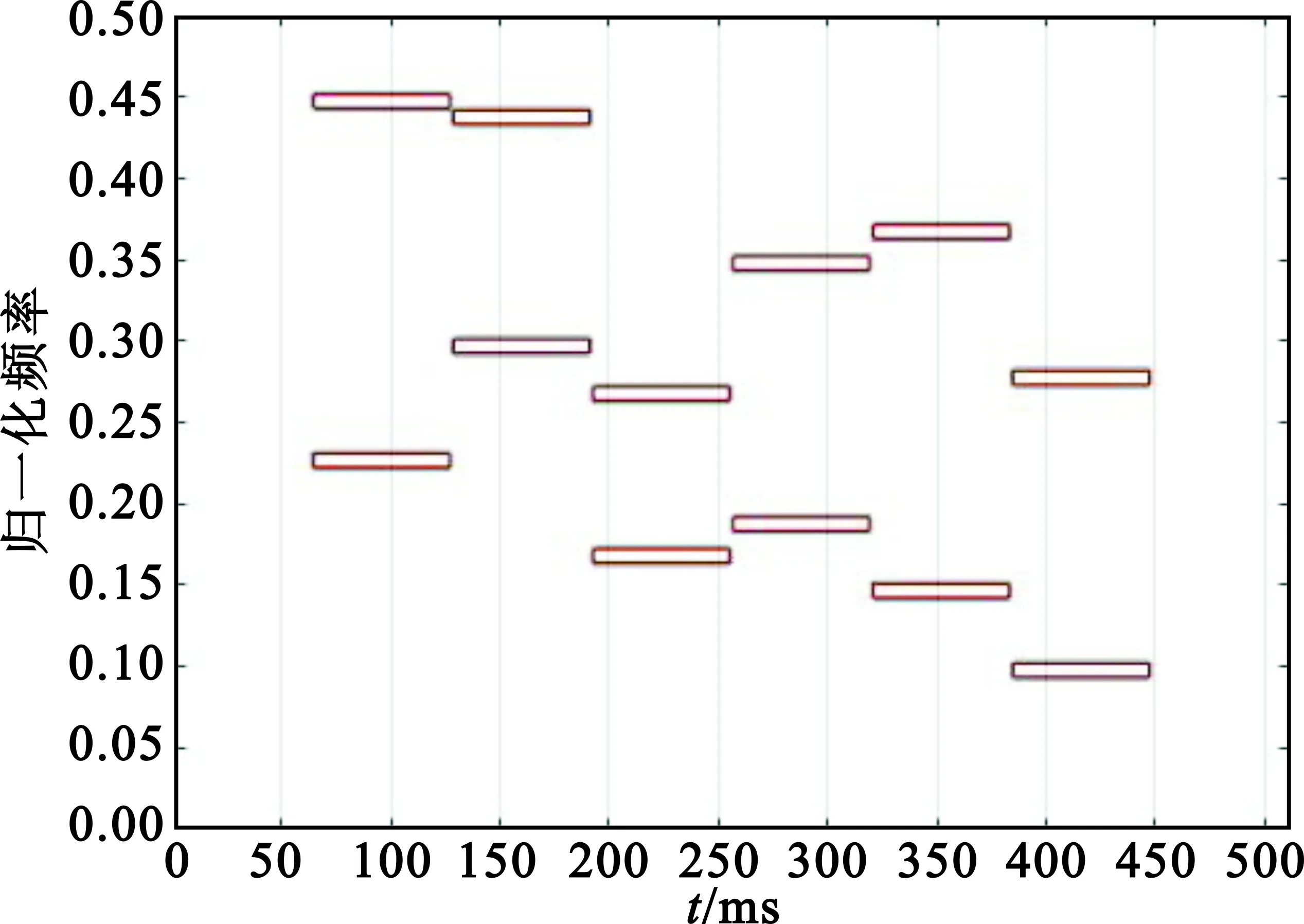
图6 信号特征提取结果Fig.6 Extraction of signal characteristics
计算得到分离矩阵B-1:
分离结果如图7所示,可以看出经过分离信号与源信号相比,可以验证分离算法的有效性,信号主要是在幅度上发生了变化。
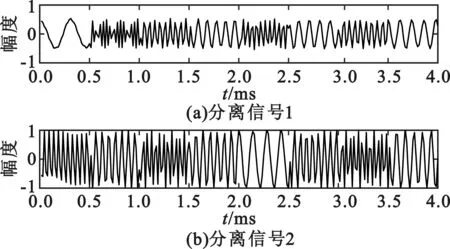
图7 分离信号的时域表示Fig.2 Separated signals in time-domain
实验表明,当信号数目增多,SPWVD分布的交叉项增加,分离效果变差,必须采取提高采样率和运算时长来提高性能,但信噪比降低对分离效果的影响并不显著。
在跳频信号盲分离方面,ICA算法是广泛应用的方法之一。ICA算法有两个关键问题:目标函数与优化算法设计。在众多优化算法中,快速独立成分分析(FastICA)因其收敛速度快、不需要知道源信号的概率密度函数、计算量小等优点得到了广泛的应用[13]。通过仿真,我们将本文算法与FastICA算法进行了对比。
两种算法分离后的信号与源信号的相关性如表2所示。
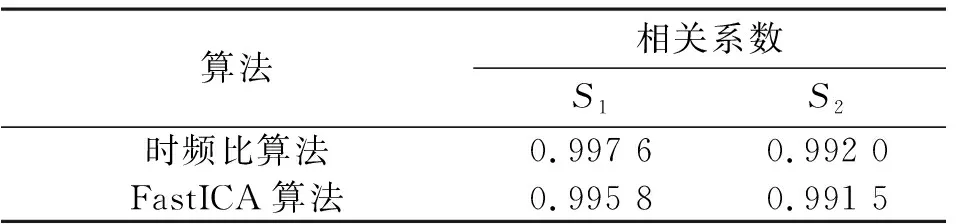
表2 不同算法得到的分离信号与源信号的相关系数Tab.2 Correlation coefficient between source signals and separated signals
6 结束语
本文提出了一种基于SPWVD的跳频信号特征提取方法,在此基础上,应用STFT时频比方法实现了对同步组网电台跳频信号的盲分离。该方法充分利用同步组网跳频信号的特点,较好地克服了利用估计跳频信号参数对跳频信号进行分离的局限性。仿真实验表明,该方法仍能在较小的计算量下有效分离同步组网跳频信号,且具有较好的实时性。但是,当信号数量较多时,由于时频分布交叉项的影响,分离效果变差,因此下一步可对此进行更加深入的研究。
