一种复合局部与非局部梯度的图像去噪变分模型
2018-12-19洋1杨平先1黄坤超2陈明举1
吴 洋1,杨平先1,黄坤超2,陈明举1,张 雷
(1.四川理工学院 自动化与电子信息学院,四川 自贡 643000;2.中国西南电子技术研究所,成都 6100362; 3.航空工业成都飞机工业(集团)有限责任公司,成都610092)
1 引 言
图像在获取、传输等一系列过程中不可避免地受到噪声的干扰,在很多领域中又需要清晰的、高分辨率的图像,因此,图像去噪问题是图像处理最基本的研究课题之一。基于偏微分的变分模型在图像去噪中表现出较好的性能,经典的局部变分模型是由 Rudin等[1]提出的ROF模型,该模型用L1范数空间描述图像梯度信息,并利用图像梯度控制扩散速率以实现图像去噪,同时较好地增强图像的结构轮廓信息。由于ROF模型通过极小化局部梯度实现去噪,不可避免地模糊图像的纹理细节信息,并在图像的平滑区域产生阶梯效应。针对ROF模型的缺点,先后出现了一些改进模型,如不同的图像特征区域采用不同的扩散方式的前后向扩散变分模型[2]、基于图像方向特性的变分模型[3]以及基于Lp范数的自适应全变分模型[4]等。这些模型在一定程度上提高了图像的去噪性能,但无法克服局部梯度的局限性,未能有效利用图像相邻区域的信息。
Buades等人[5]利用图像相似块的信息,将非局部均值滤波理解为一种几何扩散模型,引入正则化技术建立非局部变分模型,该模型通过极小化非局部梯度的L2范数以实现图像的去噪。Gilboa等人[6-7]对该模型进行研究,将非局部化G空间的概念引入到非局部均值滤波模型中,提出了基于L1范数的非局部梯度的变分模型(Nonlocal Total Variation,NLTV),并通过理论与实践证明非局部变分模型比局部变分模型具有更好的图像去噪性能,有效地重构图像的重复细节信息,克服阶梯效应。但非局部变分无法重构孤立的图像区域信息,模糊图像的轮廓信息。为同时利用局部变分与非局部变分的优点,文献[8]针对核磁共振图像的特性,采用局部与非局部变分交替迭代,有效地增强了核磁共振图像。该方法采用局部与非局部变分交替进行,在每次迭代中不可避免局部与非局部变分的缺点,因此,对常规图像处理效果并不理想。文献[9]将局部变分与非局部变分分别作用于图像的纹理部分与结构部分,以提高图像的去噪性能。该方法涉及到图像不同成分的分解与极小化,运算量较大,且在强噪声干扰下,图像的纹理与结构成分分解困难,从而造成去噪性能下降。
针对上述方法的不足,为充分利用局部变分增强图像的轮廓边缘与非局部变分能有效重构图像的纹理信息的优点,本文构建了一种同时极小化图像局部梯度与非局部梯度的复合变分模型,并给出了该模型的Bregman求解过程。该模型通过限制每次迭代后的图像接近原始图像的情况下,同时极小化图像局部梯度与非局部梯度,使去噪后的图像具有局部变分与非局部变分的优点。对比实验证明本模型能有效地重构图像细节信息,增强图像轮廓,获得更好的去噪性能。
2 局部与非局部变分去噪模型
图像的获取、传输不可避免地受到干扰,获得的噪声图像可以表示为
f=u+n。
(1)
式中:f是获得的噪声图像,n为干扰噪声。图像在有界变分空间Ω×Ω∈,全变分通过最小化图像泛函获得估计的图像u。Rudin等人通过极小化图像梯度L1范数,提出了经典的变分模型(ROF模型):
(2)

图1 Cameraman图像TV与NLTV去噪的结果Fig.1 Cameraman image before and after denoising
非局部变分是近几年兴起的图像处理技术,通过极小化非局部梯度L1范数实现去噪后的图像逼近原图。非局部变分模型为
(3)
(4)
wf(x,y)为以x、y为中心的相似两块权值函数,表达式为
(5)
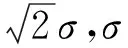
非局部梯度考虑到图像相似块的信息,利用相似块的信息获得去噪图像,能够消除局部变分的阶梯效应,重构重复的细节信息。然而,对于孤立图像区域,非局部变分无能为力,从而造成对图像孤立轮廓的破坏,如图1(c)红色椭圆区域。
为有效利用局部与非局部变分的优点,我们构建一个同时极小化图像局部与非局部变分的复合变分模型(Local and Nonlocal Total Variation,LNLTV),该模型表达式为
(6)
该模型同时极小化图像的局部梯度与非局部梯度的L1阶范数,限制项使去噪后的图像逼近原始图像。因此,该模型兼顾局部变分与非局部变分的优点,能消除局部变分的阶梯效应并增强重复纹理信息,克服非局部均值对图像轮廓的破坏。
3 局部与非局部变分模型数值求解
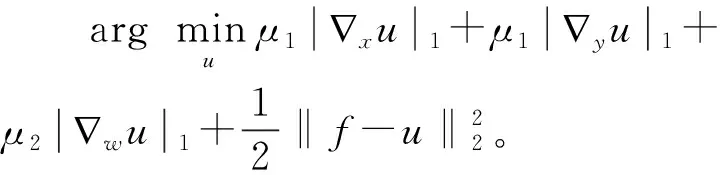
(7)
借助于分裂Bregman迭代求解L1范数约束问题,用bw代替wu,bx代替xu,by代替yu,引入松弛因子dx、dy、dw与限制项参数λ1、λ2,式(7)带限制项的极小化问题可进一步表示为



(8)
(9)
(10)
(11)
采用交替极小化求解式(8)中的bx、by、bw[11],可得
(12)
(13)
(14)
式中:shrink(u,δ)=sign(u)max(0,u-δ)。u极小化迭代求解,可以对式(8)求导,并令其导数为0,有
(15)
从而可以得到uk+1的迭代求解表达式为
uk+1=(1+λ1Δ+λ2Δw)-1·

(16)
综上所述,可以得到LNLTV模型的分裂Bregman迭代求解步骤如下:
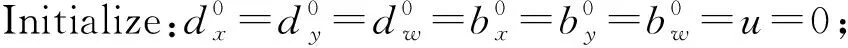
While ‖uk+1-uk‖2>toldo
Gauss-Seidel算法求解uk+1
end while
4 试验结果与分析
为证明本文的复合局部与非局部梯度的LNLTV模型去噪性能,将本文提出的LNLTV模型与ROF变分模型、NLTV模型以及文献[8-9]的联合局部梯度与非局部梯度的变分模型进行对比分析。实验采用CPU为 Intel i7、4 GB内存的的台式电脑,操作系统为64位Windows 10,各个模型程序由Matlab编写。在实验所涉及到的非局部变分模型中,对于像素点x的相似区域搜索范围限制在以x为中心的21×21区域,相似区域大小为5×5方形区域,迭代停止条件为tol≤0.001。在LNLTV模型中,参数μ1=μ2=0.25,λ1=λ2=0.01。选用标准图Lena、Women、Texmos、Cameraman进行对比实验,如图2所示。

图2 实验中选用的标准图Fig.2 Original images for experiments
采用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)、结构相似度(Structural Similarity Index,SSIM)与运算时间t作为客观评价指标。表1~3给出选用的标准图片在不同强度噪声干扰下采用不同变分模型去噪的结果,可以看出,ROF模型去噪后的PSNR与SSIM最低,这是由于ROF模型采用局部梯度,未能有效利用图像的相邻信息;相对于ROF模型,NLTV模型PSNR与SSIM提高较明显,运算时间t相对较大,这是由于NLTV模型利用图像相似区域的信息去重构图像,去噪性能有一定的提高,但相似度的寻找计算量大、耗时多。文献[8-9]与本文的LNLTV模型都综合利用局部变分与非局部变分的优点,相对于NLTV模型,PSNR与SSIM都有一定的提高。其中,文献[9]获得最大的2组PSNR与SSIM,其余10组最大的PSNR与SSIM由本文的LNLTV模型获得。进一步观察发现,在强噪声干扰下(σ=40),本文的LNLTV模型的PSNR值高于文献[9]的PSNR值0.5 dB以上,去噪提高效果明显。另外,在运行时间方面,本文LNLTV模型运算时间约为文献[9]的一半。综上分析,在客观评价方面,本文提出的LNLTV模型表现最优,这是由于本文的LNLTV模型将局部变分与非局部变分同时作用于图像,在迭代过程中更好地保留各自的优点,在有效地增强图像轮廓的同时更好地重构相似区域的信息。
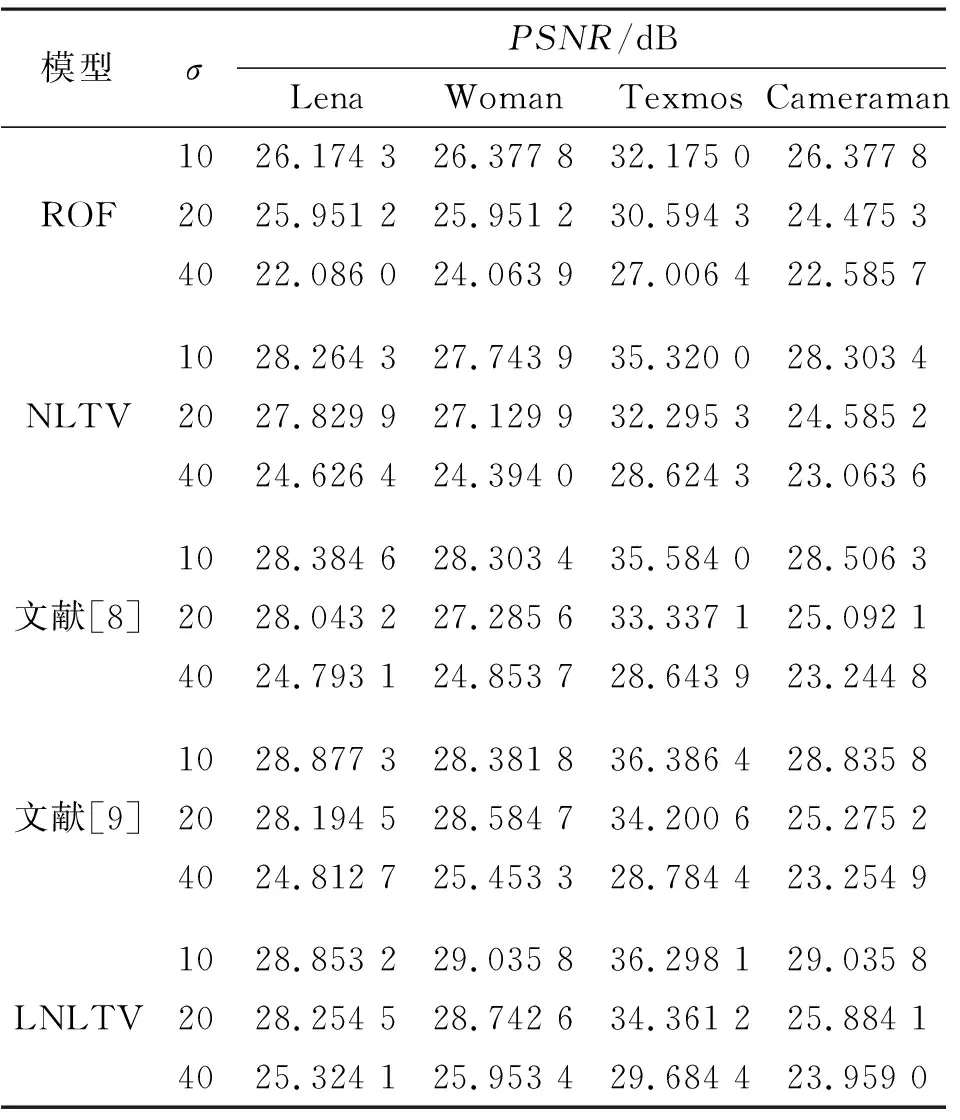
表1 不同图片不同模型去噪后的PSNRTab.1 PSNR of different images after denoising with different models
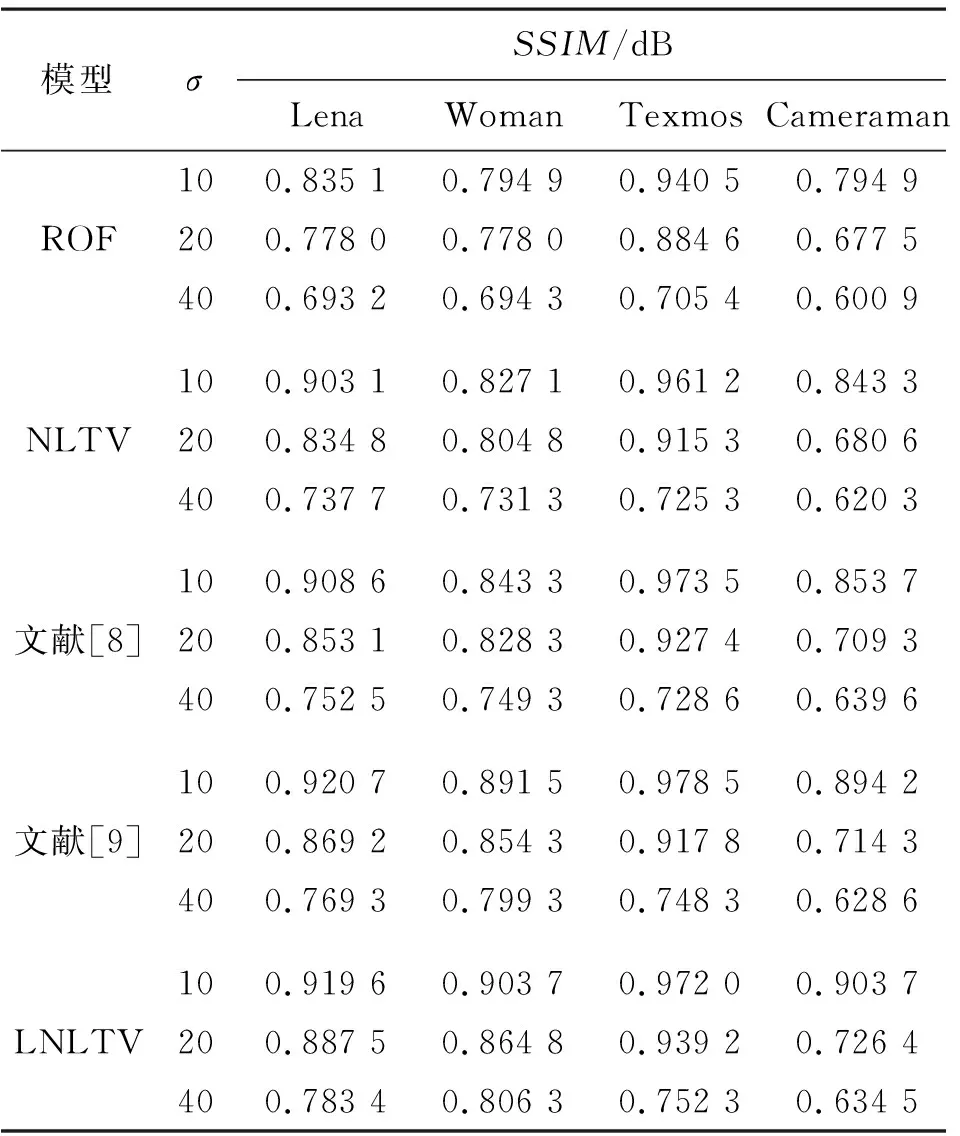
表2 不同图片不同模型去噪后的SSIMTab.2 SSIM of different images after denoising with different models

表3 不同图片不同模型的去噪时间Tab.3 Computation time of different models
图3给出了Texmos图像在受高斯噪声污染下(σ=20)采用5种模型去噪后的图像与残差图像,误差图像为去噪后图像与原始的差值。通过图3可以观察在噪声干扰情况下各种模型对图像平滑区域与边界的影响情况。从图3(b)中可以看出,ROF模型在平滑区域存在严重的阶梯效应。NLTV虽然克服了ROF模型的阶梯效应,但对图像的边缘轮廓造成了破坏(图3(c)中残差图像轮廓明显)。文献[8]方法对图像的轮廓保护较好,平滑区域仍然存在较大的残留噪声(图3(d)所示)。文献[9] 方法(图3(e))与本文的LNLTV(图3(f))在噪声的去除与图像信息保持方面表现较好,比较两者的误差图像可以看出本文的LNLTV能更好地重构图像的细节。

图3 Texmos图像去噪前后的结果(σ=20)Fig.3 Texmos image before and after denoising(σ=20)
图4给出了Lena图像在受高斯噪声污染下(σ=30)各模型去噪后的局部放大图。通过帽子区域的对比观察可以发现,ROF模型去噪后的图像细节模糊严重,NLTV模型能保持图像的一些细节,文献[8]方法增强帽子边缘的同时模糊图像较小的细节,文献[9]方法与本文的LNLTV模型在细节保持方面表现最好。

图4 Lena图像去噪前后放大图(σ=30)Fig.4 Zoomed version of the denoised Lena image(σ=30)
图5和图6给出了Woman与Cameraman在强噪声污染(σ=40)下去噪后的局部放大图。对去噪后图像的细节部分(图5中头巾区域、图6中照相机区域)进行对比观察,再一次证实,ROF模型去噪后的图像细节模糊严重,NLTV模型破坏图像的轮廓,文献[8]方法的结果存在大量的噪声且对边界造成了破坏,文献[9]方法边界保持较好,但平滑区域仍存在大量的噪声。本文的LNLTV去噪图像的残留噪声最少,同时图像轮廓也较好地保持。因此,在强噪声干扰下,本文提出的LNLTV模型在去除噪声的同时更好地保留了图像信息,去噪性能最优。

图5 Woman图像去噪前后放大图(σ=40)Fig.5 Zoomed version of the denoised Woman image(σ=40)

图6 Cameraman图像去噪前后放大图(σ=40)Fig.6 Zoomed version of the denoised Cameraman image(σ=40)
5 结束语
本文针对局部变分模型模糊图像的细节、在图像的平滑区域产生阶梯效应,以及非局部变分模型对图像的结构轮廓破坏的缺点,提出了一种复合局部梯度与非局部梯度的变分去噪模型。在确保去噪后的图像接近原始图像的情况下,采用分裂Bregman迭代极小化图像局部梯度与非局部梯度的L1范数实现模型的求解。与经典ROF变分模型、NLTV模型以及复合变分模型进行对比分析证明,本文提出的基于局部与非局部梯度的变分模型兼顾局部与非局部变分的优点,能更好地重构图像的细节信息,增强图像的轮廓,去除平滑区域的阶梯效应。因此,本文提出的复合变分模型具有更好的应用前景。另外,将局部与非局部变分相结合应用到特殊图像处理中,如遥感图像、电子显微图像、红外图像等相关领域,是将来研究的重点。
