基于毫米波大规模MIMO系统的混合预编码设计
2018-12-19
(南京邮电大学 通信与信息工程学院,南京210003)
1 引 言
随着移动通信技术不断完善和无线设备的广泛使用,无线网络容量呈指数增长。特别地,即将在2020年进行商用部署的5G,预计能够满足移动互联网流量增加1 000倍的需求,峰值理论传输速率可达10 Gbit/s[1-2],传统的通信频段已经很难达到上述要求。毫米波通信技术是未来无线通信技术的主要候选方案之一。虽然毫米波在自由空间损耗很大,但是通过毫米波大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)系统产生的定向波束成形增益可以对抗自由空间的路径损耗。
在传统的MIMO系统中,基带预编码器采用纯数字预编码器结构,这种结构需要每个射频(Radio Frequency,RF)链路连接每根天线,同时也包括和天线数目一样多的数模转换器和模数转化器。对于毫米波大规模MIMO系统,由于天线数目众多,部署大量RF链路会产生很高的成本和功耗。为了减少RF链路的数量,一些研究者提出一种由模拟预编码器和数字预编码器组成的混合预编码器结构。模拟预编码器是通过可以控制相位和幅度的移相器组成,数字预编码器通过RF链路实现。通常情况下,存在两种混合预编码器结构:全连接结构,每个RF链路与每根天线相连;部分连接结构,每个RF链路只与部分天线相连。文献[3]还提出了另外一种混合预编码器,通过将部分连接结构与全连接结构整合在一起进行设计分析。在学术界,大部分文献集中在全连接结构混合预编码器的研究[4-6]。
相比于全连接结构,部分连接结构由于较低的硬件复杂度,在天线部署中更加实用。文献[7]将模拟预编码器和数字预编码器固定其中一个,利用交替最小化算法,单独求最佳模拟/数字预编码器。该算法需要运用半定松弛原理和黎曼流型相关公式,涉及到的数学计算十分繁琐。文献[8]首先考虑在无约束条件下求最优化问题,然后根据最小均方误差(Minimum Mean Square Error,MMSE)准则,利用选择性算法生成满足之前假设条件的一个预编码矩阵。这种算法需要在模拟和数字波束成形矩阵之间进行迭代,随着基站发送天线数目的增加,迭代次数也在不断增加。文献[9]利用基于连续信道干扰消除(Successive Interference Cancellation,SIC)的方法,提出了一种接近最佳性能的混合预编码算法。这种算法是通过求出第一个到最后一个RF链路连接子天线阵列所能实现的最大频谱效率,然后通过迭代方法,从而实现整个混合预编码器最大的频谱效率。但是,文献为了简化计算复杂度,将数字预编码矩阵假设为一个对角矩阵,这样有失一般性,并且会使得整个混合预编码器的性能下降,与纯数字混合预编码器性能差距明显。
本文通过研究基于部分连接结构的毫米波大规模MIMO系统的混合预编码设计,采用分层设计模拟预编码器和数字预编码器。仿真结果表明,根据所提算法设计的混合预编码器可以接近纯数字预编码器的性能,并且优于文献[9]提出混合预编码器的性能。
2 系统模型与信道模型
2.1 系统模型
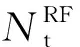

图1 混合预编码器结构比较Fig.1 Hybrid precoder structure comparison
(1)
式中:y∈Nr×4代表接收信号;ρ代表平均接收功率;H∈Nr×Nt表示信道矩阵,根据文献[4],信道矩阵H满足E⎣表示均值为0、方差为σ2的加信高斯白噪声;s∈Ns×1表示发送数据流符号向量,且有
(2)
为了能够实现预编码,假设信道矩阵H对于基站和移动台都是已知的。由于毫米波在信道传播中的有限散射性,可以通过压缩感知算法对毫米波信道进行信道估计[10]。本文主要集中在毫米波大规模MIMO系统的混合预编码设计,并且假设移动台接收机能够正确解码。因此,当发送信号服从高斯分布时,系统实现的频谱效率可以表示为
(3)
式中:P代表总的混合预编码矩阵,即P=AD。本文主要考虑两种约束:
约束1:由于部分连接结构的每个RF链路只连接M根天线,并且每个天线子阵列之间是互不影响的,因此,模拟预编码器矩阵可以定义为
(4)

约束2:基站总功率约束满足
(5)
有些文献直接将式(5)取等号,这是不严谨的,因为求解系统最佳的混合预编码设计问题应该是一个区域最优化问题。
2.2 信道模型
由于毫米波信道的有限散射性,有些研究者称之为簇信道,本文采用文献[4]使用的扩展Saleh-Valenzudela模型,离散时间窄带信道矩阵H可以表示为
(6)
式中:L表示基站和移动台之间毫米波传播路径的数量,并且假设每个簇能够产生单个传播路径;αl表示第l条传播路径的复增益;θl、φl代表第l条传播路径的到达角和离开角;fr(θl)和ft(φl)分别表示系统收发两端的天线阵列响应向量。对于均匀线性阵列(Uniform Linear Array,ULA),天线阵列响应向量可以表示为
(7)
(8)
式中:λ表示毫米波波长,d表示相邻天线之间的空间距离。
3 基于部分连接结构的混合预编码设计
本文假设移动台接收机能够正确解码,所以主要集中在基站发射机混合预编码设计问题。根据上述分析,假设存在AD能够接近最佳无约束的混合预编码器Popt,那么问题(3)可以等价为
(9)
根据文献[4],假设信道矩阵H的奇异值分解为H=U∑VH,并且有
(10)
式中:Σ1是Ns×Ns维矩阵;V1是信道矩阵H右边奇异值矩阵V的前Ns列,即V1∈Nt×Ns。那么当满足以下条件时,最佳无约束混合预编码器Popt=V1。
(11)
(12)
对于式(9)的非凸规划问题,文献[4]试图寻找一对模拟预编码器和数字预编码器,提出一种正交匹配追踪算法设计最佳混合预编码器。本文分析基于部分连接结构,采用联合设计模拟预编码器和数字预编码器的方法是否可行。
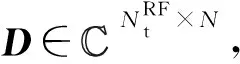
(13)
由于P=AD,根据式(5)和式(13),总体预编码器矩阵P可以表示为
(14)
从式(14)可以观察到,由于模拟预编码器矩阵A的约束,其模值为1,所以混合预编码矩阵P每列元素的幅度取决于D每列元素幅度。将式(14)得到的矩阵P代入式(9)可以发现,在约束(4)和(5)条件下,联合求AD从而实现最佳混合预编码器Popt的方法是不可行的。为此,需要采用分层设计思想。
采用分层设计,第一层设计模拟预编码器A,当A确定后,第二层设计数字预编码器D。根据这种思路,则起始的最优化问题可以表示为
(15)
假设模拟预编码器A已经确定,那么可以通过将Heff=HA看成是一个等效信道,式(15)可以进一步写成
(16)
对于式(16)的最优化问题,可以通过注水算法获得最佳数字预编码器:
Dopt=Q-1/2UeΓe。
(17)
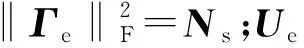
HeffQ-1/2=Heff(AHA)-1/2=M-1/2Heff。
(18)
那么可以得出结论1:Ue也可以表示等效信道M-1/2Heff的右边奇异向量的前Ns列。将求出的Dopt代入式(16),结果表示为
(19)
根据结论1,令M-1/2Heff前Ns列奇异值分解:
(20)
因此,结合公式(19)和(20),目标函数进一步化简得到
(21)
式中:Σ=diag(σ1,σ2,…,σNs),σ1≥σ2≥…≥σNs表示M-1/2Heff矩阵的前Ns个奇异值。通过式(21),可以得出结论2:式(9)的最优化问题求解转换为求M-1/2Heff的奇异值矩阵。当信道矩阵H确定时,M-1/2Heff主要由模拟预编码器A决定。
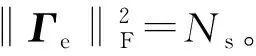
(22)
但是,式(22)是一个非线性最优化问题,很难直接求出最佳模拟预编码器A。注意到

(23)
因此,问题(22)进一步转化成
(24)
(25)
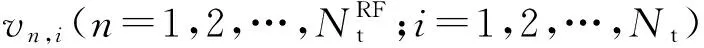
(26)

由式(26)可以看出,起始的最优化问题可以看成是在每根天线功率分配的约束下,单个RF链路连接天线子阵列最优化问题,即

(27)
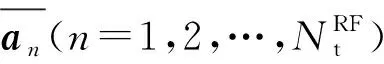

(28)
式中:gmk是矩阵G的第m行第k列;pm代表每个RF链路连接天线子阵列每根天线分配的功率,当同等功率分配时值为1;ψ(w)代表复变量w的相位,

初始化:随机产生满足公式(4)条件约束的矩阵A,s=1,p1,p2,…,pM=1。
(1)奇异值分解H=UΣVH,求出V和对应的前Ns个奇异值σi。
(2)求出矩阵G。
for 1≤m≤M
end for
s++
if(s≤S) continue;if not,break;
end if
end for
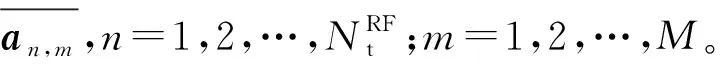
对本文提出的算法进行复杂度分析。本文算法复杂度可以分为三部分:第一部分是信道矩阵的奇异值分解,注意到H∈Nr×Nt,这部分的算法复杂度为第二部分是利用注水算法求Dopt,算法复杂度为第三部分为计算矩阵G和利用迭代方法求算法复杂度为因此,本文提出算法总体复杂度为对于文献[9]提出的算法,在每次进行迭代时,算法复杂度为O(NtM3)。因此,在同样迭代次数最大为S的条件下,本文提出的总体算法复杂度小于文献[9]总体算法复杂度。
4 实验仿真与分析
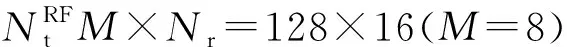
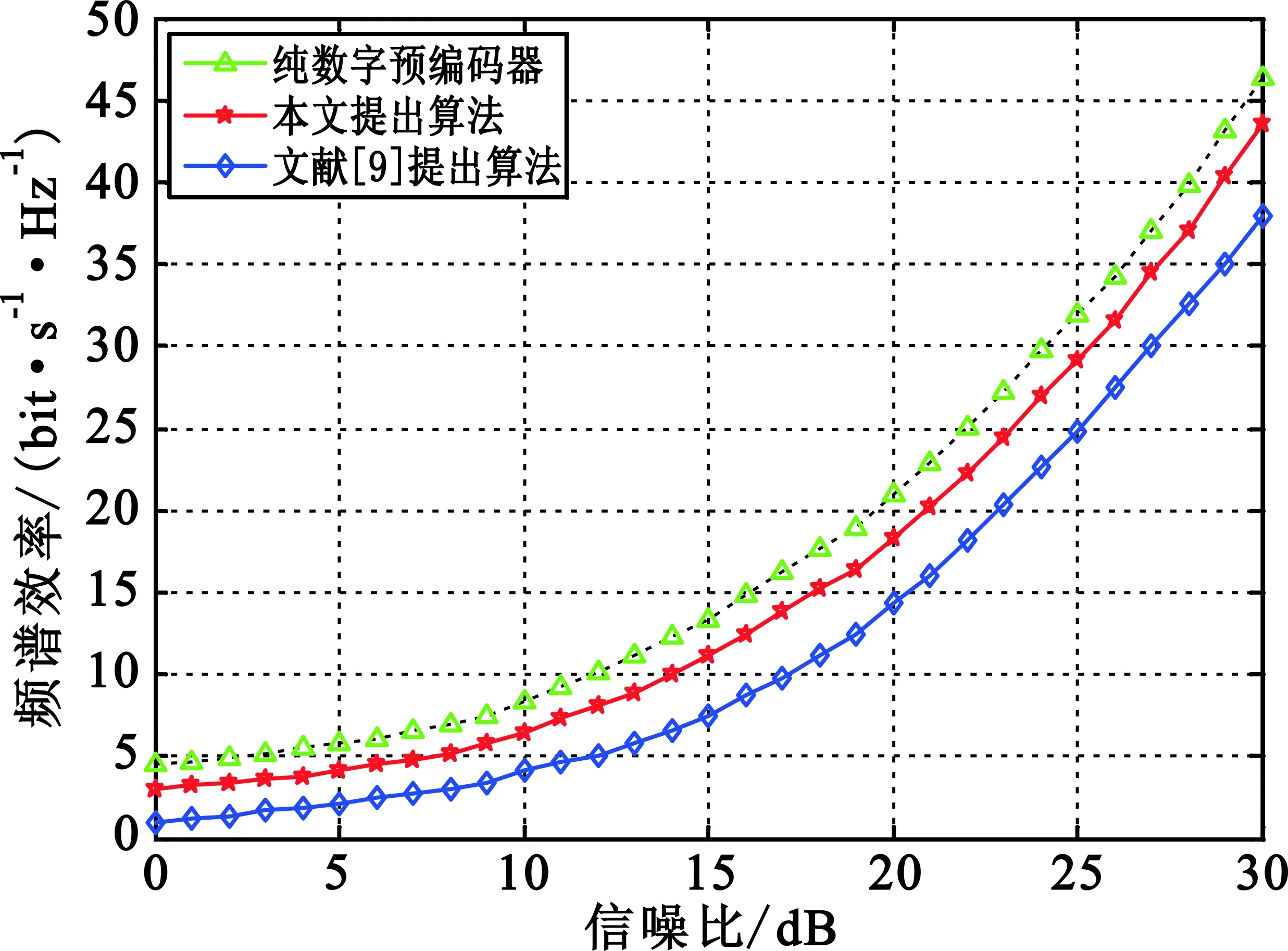
图毫米波大规模MIMO系统性能Fig.2 Performance of millimeter-wave massive MIMO system with Nt=128,Nr=16,M=8
从图2可以观察到,当RF链路的数量为16并且每个RF链路连接8根天线时,本文所提算法设计的混合预编码器接近纯数字预编码器的性能。当信噪比为30 dB时,本文所提算法使得毫米波大规模MIMO系统实现的最大频谱效率能够达到纯数字预编码器最大频谱效率的94%。但是对于文献[9]提出的算法,作者一开始就假设数字预编码器矩阵为对角矩阵,这种假设会有失一般性,从而使得整体的混合预编码器的性能带来损失。图2表明,文献[9]算法在信噪比为30 dB时,实现的最大频谱效率只能达到纯数字预编码器最大频谱效率的82%。同时,当信噪比为0 dB时,本文所提算法使系统能够实现的频谱效率比文献[9]算法实现的频谱效率高2 bit/s/Hz。

图毫米波大规模MIMO系统性能Fig.3 Performance of millimeter-wave massive MIMO system with Nt=128,Nr=32,M=4

(29)
式中:ξ∈[0,1]表示信道状态信息的精确度,E表示服从N(0,I)分布的矩阵[12]。

图4 不同信道状态信息,毫米波大规模MIMO系统性能Fig.4 Performance of millimeter-wave massive MIMO system in different channel status information with Nt=128,Nr=16,M=8
5 结束语
本文通过对比分析单用户下行链路毫米波大规模MIMO系统常见的两种混合预编码器结构,综合考虑硬件成本、硬件复杂度和功率消耗等因素,选择部分连接结构的混合预编码设计。本文在设计最佳模拟预编码器和数字预编码器的过程中,并没有像许多文献一样采用联合设计方案,而是提出了一种分层设计思路。仿真结果表明,根据本文提出算法设计的最佳混合预编码器的性能比文献[9]更加接近纯数字预编码器的性能。同时,在不同理想信道状态信息条件下对所提出算法进行仿真分析的结果表明,即使在信道状态信息精确度很低的情况下,系统也能实现很高的频谱效率。未来的工作将集中在多用户场景下毫米波大规模MIMO系统的混合预编码设计,因为多用户毫米波通信在实际生活中更为常见。
