LoRa调制技术及解调算法
2018-12-19刘树聃1孙继炫
刘树聃1,2,孙继炫
(1.许昌市耕新信息科学研究院,河南 许昌 461000;2.许昌职业技术学院 航空工程学院,河南 许昌 461000; 3.北京理工大学 自动化学院,北京 100081)
1 引 言
近年来,随着智能设备的发展,物联网(Internet of Things,IoT)[1-3]概念被广泛提出并被大规模应用于各个行业。物联网旨在解决物与物、物与人之间的连接及信息交换。从应用场景而言,物联网主要分为两类:诸如智能家居、工业数据采集等区域网通信场景,这类应用主要采用短距离通信技术,如Zigbee等;广范围、远距离的通信应用场景,这类应用则需要广域网通信技术支持。为了满足物联网中的低带宽、低功耗、远距离以及大量节点的连接需求,业界提出了低功耗广域网(Low-Power Wide-Area Network,LPWAN)技术。
目前,LPWAN技术主要有LoRa、SigFox、LTE Cat-m、NB-IoT等[4-5]。其中,LoRa是目前应用前景非常看好的一种LPWAN技术。该技术起源于Semtech公司,目前已形成LoRa联盟,旨在通过构建生态系统推动LoRa的普及。该联盟也是LPWAN领域的第一个产业联盟,中兴、中科院等国内大公司及研究机构均为该联盟成员,正在大力推进LoRa技术的应用普及。LoRa的专利[6]由Semtech公司拥有,专利文件中并没有对详细技术细节包括核心的调制技术进行描述。此外,目前公开发表针对LoRa技术的文献寥寥无几,仅有的也是对LoRa协议进行研究[7-9],而对物理层算法的研究几乎没有。为此,本文将针对LoRa的调制解调技术原理进行详细的数学描述,并给出具体的调制解调算法。
2 LoRa调制技术
LoRa调制是基于线性调频扩频(Chirp Spread Spectrum,CSS)的技术[10]。因为CSS技术作为物理层技术可以有效实现低功耗和低复杂度的要求[11],同时其脉冲压缩和扩频通信可以提供长距离可靠通信[12],与传统CSS技术相比LoRa调制进一步改善了其频谱利用率[13-14],其本质是对基本Chirp信号进行循环移位得到调制信号,每个符号起始位置的初始频率偏移承载所需传输的信息,而Chirp信号仅仅作为类似于一种载波信号。相比于传统的直接序列扩频(Direct Sequence Spread Spectrum,DSSS)通过扩频因子(Spreading Factor,SF)将一个数据比特分割为NSF个码片进行扩频传输,LoRa调制将NSF个数据比特分割为 2NSF个码片进行扩频传输,其码片速率Rc及比特速率Rb定义为[3]
(1)
式中:B为调制带宽,NSF取值为6~12。
基本Chirp信号数学表达式如下所示:
(2)
式中:φ(t)为Chirp信号的相位;fc为载波频率;Ts为信号扫频时间,即符号周期;μ>0表示上扫频,即Up Chirp信号;μ<0表示下扫频,即Down Chirp信号,一般取μ为1或-1。
由式(2)可知,Chirp信号的瞬时频率为
(3)
如前所述,LoRa调制信号由Chirp信号进行循环移位获得。假设采用向左偏移循环移位方式[15],则LoRa调制信号的瞬时频率为
(4)
式中:K为循环移位值,即偏移的码片数,可由下式得到:
(5)
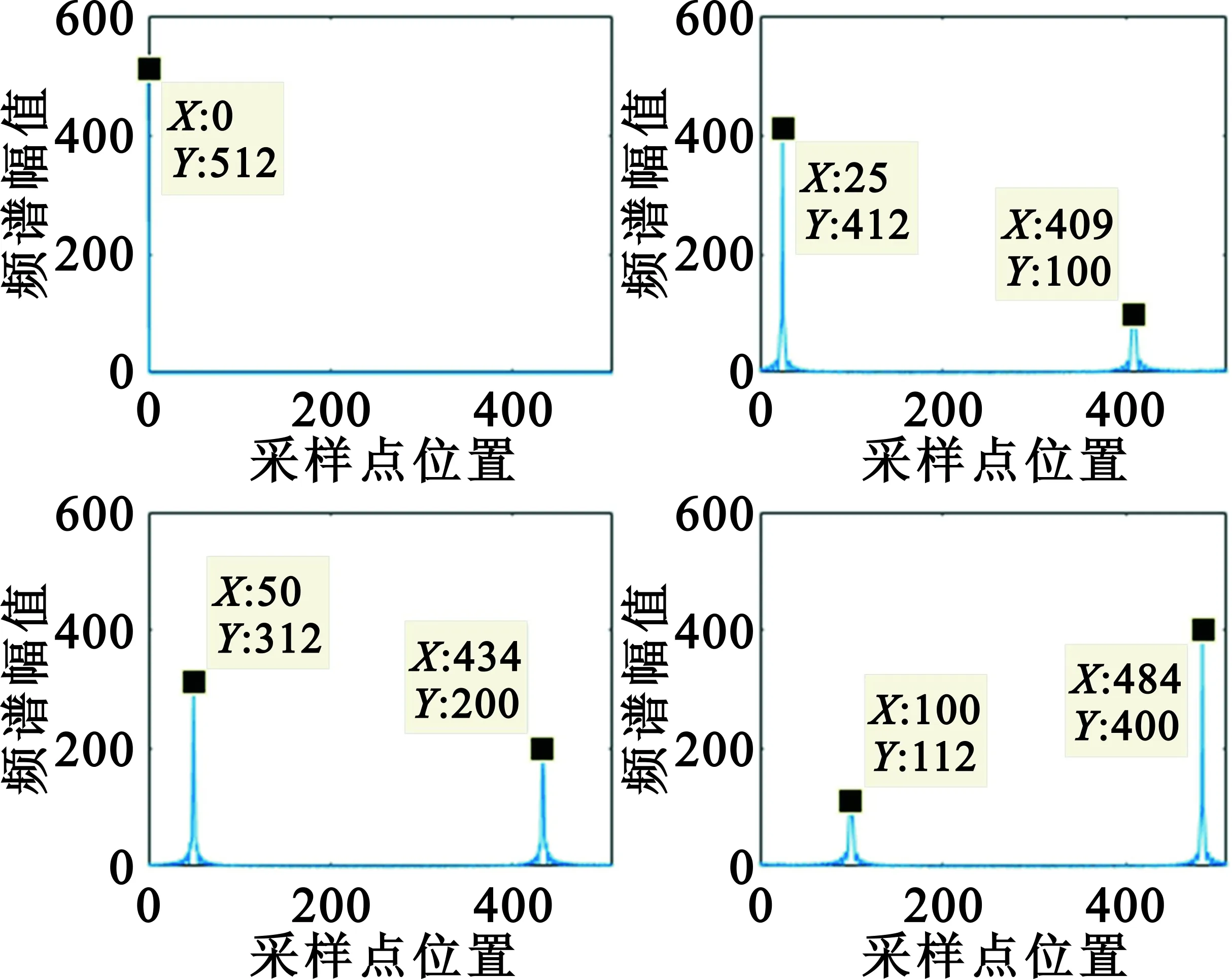
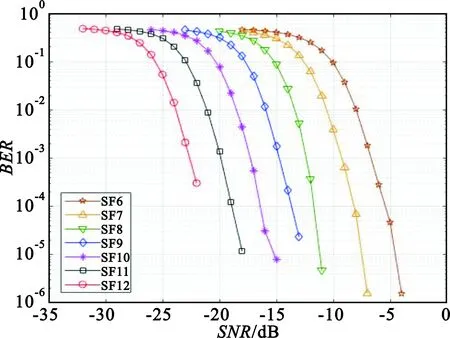
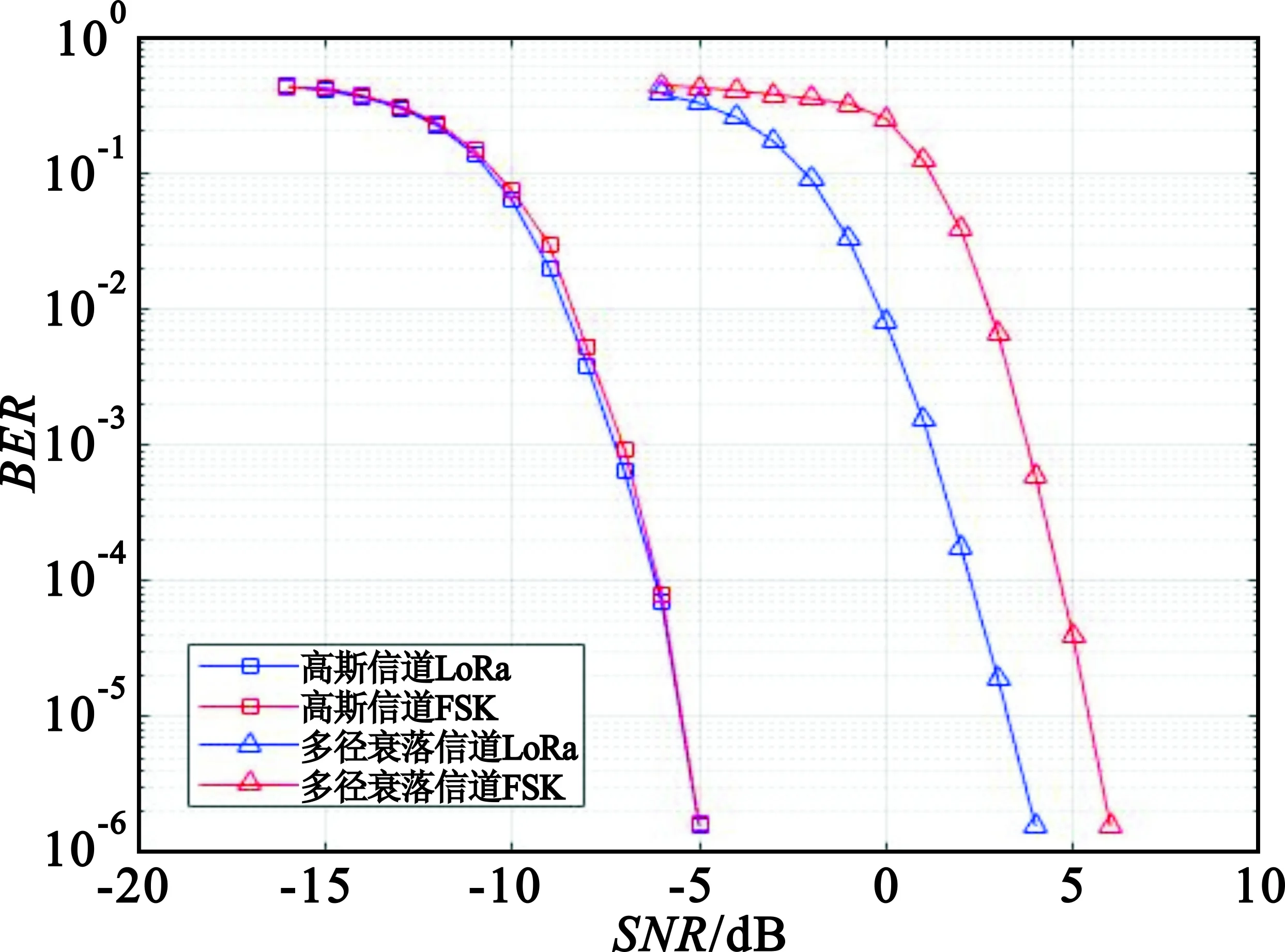
V=[v0,v1,…,vNSF-1]是由NSF个数据比特组成的向量,即所需传输的信息比特,其由式(5)调制成一个符号进行发送。由于一个符号包含2NSF个码片,则有0 结合式(3)和式(4),即可得出LoRa调制的信号波形为 (6) 图1所示即为LoRa调制信号的时域波形图及时频图,采用Up Chirp信号。其中,扩频因子NSF为7,调制带宽B为125 kHz,循环移位值K分别为0、25、50和100。根据上述分析可知,每个LoRa调制信号可以传输7 bit信息数据,且由式(5)可知,传输的比特信息分别为0000000、0011001、0110010和1100100。 图1 LoRa信号时域波形图及时频图Fig.1 LoRa signal time-domain waveforms and time-frequency graphs 根据如上所述的LoRa调制原理及Chirp信号的特征,基本思路是采用匹配滤波的方法对LoRa调制信号进行解调。 在接收端,对如式(6)所示的LoRa调制信号(μ=1)与如式(2)所示的本地未调制的基本Chirp信号(μ=-1)进行共轭相乘,则接收信号波形为 srx(t)=sm(t)s*(t)= (7) 对于实际应用而言,需要对如式(7)所示的连续信号进行离散化处理。下面将分为单倍采样及多倍采样两种情况进行讨论。 假设接收端采用单倍采样方式进行式(7)描述的信号接收采样,即采样率为BHz,则采样后的离散信号为 (8) 对上式所示信号进行离散傅里叶变换(Discrete Fourier Transform,DFT),可得到其频谱为 (9) 式中:N=2NSF。由式(9)可知,对于单倍采样的情况,通过离散傅里叶变换得到的信号频谱在循环移位值K处取得峰值N,而在其余点位置处频谱值均为0。因此,利用这一特性,即可计算得到循环移位值K,进而解调得到发送比特信息。图2为对图1所示的4个LoRa调制信号采样单倍采样得到的解调结果。 图2 单倍采样解调输出Fig.2 Demodulation output of single sampling rate 当接收端采用过采样,即多倍采样进行信号接收,假设采样率为mBHz,则采样后的信号为分段离散信号,如下所示: (10) 对上式所示信号进行离散傅里叶变换,可得 (11) 可以看出,该频谱由两个等比级数之和表示。特别地,当公比为1,即k=K或k=(m-1)N+K时,取得两个极大值。因此,式(11)可以进一步表示为 (12) 式中:Θ为公比不为1时两个等比级数之和,该值接近于0。 当采用4倍采样率对图1所示的4个LoRa调制信号进行接收,并由上述方法进行匹配滤波及DFT变换后,结果如图3所示。可以看到,在如式(12)所示的两个位置处存在峰值,其余位置处的频谱值接近于0。特别地,当K=0时,两个峰值点均重合于位置0处。 图3 4倍采样解调输出Fig.3 Demodulation output of 4 times sampling rate 因此,最终的解调结果应该同时考虑两个峰值点。假设两个峰值点的位置分别为P1和P2,则最终的解调结果如下: (13) 式中:mod表示取模运算。 为了验证LoRa调制技术及本文解调算法的性能,本节对LoRa系统在加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道和多径衰落信道进行仿真验证。表1为Semtech公司在其数据手册上给出的不同扩频因子对应的接收端信噪比,表2为仿真参数设置。假设理想同步的情况下,对其进行2 000次仿真传输实验,仿真采用单倍采样实现。 表1 LoRa系统扩频因子取值Tab.1 Spreading factor of LoRa system 表2 仿真参数设置Tab.2 Simulation parameter setting 如图4所示,在高斯信道下LoRa调制的性能随着扩频因子的增大而提升,这是由于扩频因子增大带来的扩频增益的提升。此外,在误比特率为10-3时不同扩频因子所对应的信噪比与表1所给出的理论要求符合,这表明了本文解调算法的有效性。 图4 高斯信道下LoRa调制仿真性能曲线Fig.4 Performance of LoRa modulations in AWGN channel 图5给出了LoRa调制在多径衰落信道下的性能仿真曲线,此处实验采用的多径信道为Cost207多径信道模型[16]中的恶劣城区信道环境,信道条件非常恶劣。因此,相比于高斯信道,性能出现较大幅度的下降。此外,图6显示了扩频因子为7时的LoRa调制和相同码片速率情况下FSK调制性能对比曲线。可以看到,对于高斯信道,LoRa调制和FSK调制的性能接近;而在该多径衰落信道下,LoRa调制的性能明显优于FSK调制,这是因为LoRa调制是对整个频带的扫描,衰减会被平均分布,而FSK调制落在衰减较大的频带内时会对误码率产生更大的影响。因此,LoRa拥有比FSK更加优越的抗衰落性能。 图5 多径衰落信道下LoRa调制仿真性能曲线Fig.5 Performance of LoRa modulations in multipath fading channel 图6 高斯信道和多径衰落信道下LoRa调制和FSK调制仿真性能曲线Fig.6 Performance of LoRa modulations and FSK modulation in AWGN and multipath fading channels LoRa是目前工业界大力推广的一种LPWAN技术,尤其适用于大规模广域物联网应用。本文针对LoRa调制解调技术原理进行了详细的数学描述,并提出了一种基于匹配滤波的解调算法;同时,对LoRa调制技术的性能进行了高斯白噪声信道及多径衰落信道下的仿真比较。仿真结果表明,本文解调算法的性能与理论要求给出的指标相符合,验证了本文解调算法的有效性。此外,与FSK调制解调性能的仿真对比表明,LoRa调制技术拥有比FSK更加突出的抗衰落性能,验证了LoRa通信在低速率远距离通信场景的优越性。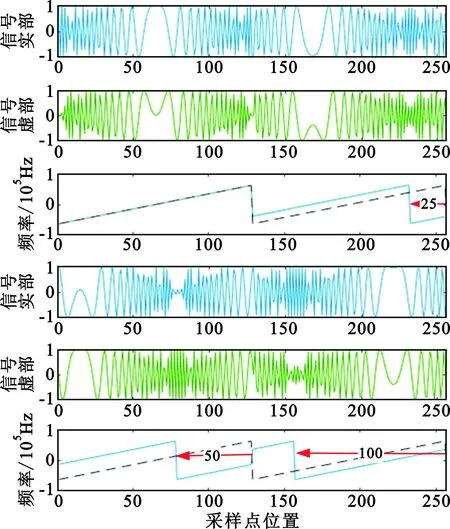
3 解调算法

3.1 单倍采样率解调
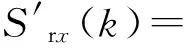

3.2 多倍采样率解调

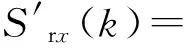
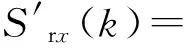
4 仿真结果


5 结 论
