跳频信号的归一化多普勒频差最大似然估计

王 旭1，谢 磊，张孔明1，何子述

(1.西南电子电信技术研究所，成都610041；2.电子科技大学 电子工程学院，成都611731)

1 引 言

跳频是最常用的扩频方式之一，应用广泛，提高跳频通信信号的无源定位性能具有重要的意义[1]。本文研究无源双站对运动目标定位涉及的跳频信号多普勒频差估计问题，而关于双站情况下利用到达时间差(Time Difference of Arrival，TDOA)和多普勒频差(Frequency Difference of Arrival，FDOA)对运动辐射源目标进行无源定位的机理在相关文献中已有论述[2-4]。

FDOA指某一运动目标相对于两个定位站的多普勒频率的差值。利用FDOA和TDOA可以实现目标定位、跟踪等[5-8]。对于运动目标的FDOA和TDOA的联合估计，常见的算法包括基于子空间的频域高分辨时差测量算法[9]、基于盲波束形成的方法[10-11]和Hough变换[12]等，而这些算法往往涉及到自相关矩阵的求逆或者谱分解，计算量比较大。文献[13-14]中提到基于最大似然估计的TDOA和FDOA估计方法，分别针对相干短脉冲信号和弱平稳的数字通信信号，并且是基于单基站的情形。而针对跳频信号，国内外有不少学者进行了研究。文献[15]提出了一种基于跳频信号特征提取参考频率点处的相位差求TDOA。这种方法从原理上讲借鉴了谱相关拟合相位的思路，估计精度较高，但要对相位解模糊，计算复杂。文献[16]基于跳频信号模型的特征，利用不同码元之间的相位差分来估计TDOA。这种算法计算效率高，但要求对载波差的估计足够精确，而该精度主要依赖于符号持续时间，往往单个符号的跳频信号持续时间较短，导致对载波差的估计不准确，并且这种方法也存在相位模糊的问题需要解决。

对于一个运动目标在某时刻发出的跳频脉冲串信号，可以认为在跳频脉冲串信号持续时间内运动目标相对于各个定位站的径向速度不变，但是由于各脉冲的载波频率不同，一个定位站接收到的跳频脉冲串信号中各个脉冲对应的多普勒频率将不一致，两个定位站各脉冲之间的多普勒频差也将不同，为充分利用跳频脉冲串中的信息量提高对跳频信号的定位性能，本文提出了跳频脉冲串信号的归一化频差最大似然估计算法，以跳频脉冲中一个跳频频率的多普勒频差为基准，利用所有跳频脉冲信号对该基准多普勒频差进行估计，随着算法中使用的脉冲信号数量增多，基准多普勒频差估计性能有明显改善。该算法避开了矩阵的谱分解和求逆运算，运行速度较快。

2 基本原理

2.1 基于双站的多普勒频差估计算法

首先假定信号为确定性的，噪声为白高斯噪声，则两个接收站接收到的信号可以表示为

(1)

式中：a为信号幅度常数，D1与D2分别表示信号源s[n]到达两个接收站的传播延迟，ω1与ω2分别表示两个接收站接收信号的频率，n为样点序号，N为样点总数。待估时差与多普勒频差参数矢量定义为

θ=[D2,1,ω2,1]T。

(2)

式中：时差D2,1=D2-D1，多普勒频差ω2,1=ω2-ω1。进而，接收信号可以等价地表示为

(3)

为了便于后续表述，首先定义观测信号矢量：

(4)

由于信号是确定的，噪声为复高斯白噪声，则观测矢量的均值满足

μ(y)=E{y}=x。

(5)

式中：

(6)

x1和x2分别满足

(7)

可见观测矢量的均值与参数θ有关。相同假设下，观测数据的协方差矩阵可以表示为

C=E{(y-E{y})(y-E{y})H}=

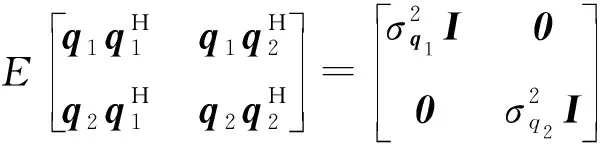
(8)

显然，观测数据协方差矩阵C与参数θ无关。为了实现对FDOA的估计，这里首先根据信号模型建立最大似然函数：

p(y;θD1,s(t))=

(9)

可以得到其最大似然估计为

(10)

(11)

式中：μ(θ)=[x1,x2]T需要估计未知信号s[n]，这里我们采用μ(θ)的估计来近似实现最大似然估计，也即

(12)

这里首先采用第一个接收站接收信号作为x1的估计，则μ(θ)的估计满足

(13)

式中：F{y1,D2,1}表示将信号y1时移D2,1，可采用时延滤波器如sinc内插器[17-18]等实现；Φ(ω2,1)定义如下：

(14)

综上，TDOA与FDOA估计为

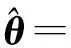
‖Φ(ω2,1)F{y1,D2,1}‖2}。

(15)

在时延相对信号持续时间较小时，对于恒模信号可认为‖Φ(ω2,1)F{y1,D2,1}‖为常数，则

(16)

这里θ=[D2,1,ω2,1]T，信号y1的延迟形式为

F{y1,D2,1}=[y1[0-D2,1],y1[1-D2,1],…,y1[N-1-D2,1]]T，

(17)

其中每个元素可采用如下方式实现：

(18)

式中：K为内插器阶数。值得注意的是，如果这里假定时差D2,1已知，则由式(16)得到频差估计表达式：

(19)

进一步，如果时差为零，则

(20)

在更一般的情况下，时差是未知的，可以采用二维网格搜索的方法得到TDOA与FDOA的解。

网格搜索的步骤如下：

Step1 确定二维网格搜索精度，将搜索区域划分为g1,g2,…,gG，G为网格数。

Step2 将第i个网格对应的向量gi赋值给未知参数θ，i初始化值为1。

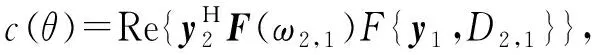
Step4 将i+1赋值给i，也即i=i+1，并重复Step 2～4，直到i=G。

Step5 将c(θ)最大值对应的搜索网格值作为参数θ的估计输出。

2.2 跳频信号归一化多普勒频差最大似然估计算法

将上面的方法应用到跳频脉冲信号形式，由于每个脉冲的载波频率各不相同，所以每个脉冲的多普勒频差也不同，于是可以将二维搜索目标函数可改写为如下表达式：

(21)

式中：Np为脉冲信号个数，y1,i与y2,i分别表示两路观测量的第i个脉冲信号矢量，

αi=fc,i/fc。

(22)

式中：fc,i表示第i个脉冲的载波频率，fc表示参考载波频率。算法所估计出的FDOA也是在参考载波频率下的FDOA，而利用该已知的参考频率与估计得到的FDOA即可计算出目标的径向速度差，或是直接使用下式估计TDOA与FDOA：

(23)

这里y1、y2与ΦΣ(ω2,1)由下面的定义式给出：

(24)

(25)

(26)

式中：y1,i与y2,i分别表示两路观测量的第i个脉冲信号矢量，对角矩阵Φ(αiω2,1)表示第i个脉冲对应的变频矩阵，其定义与式(14)相似。

多普勒频差估计的步骤如下：

Step1 读取数据，包括脉冲数、采样率、跳频图及中频脉冲信号。

Step2 通过Hilbert变换将输入中频信号转换为I/Q信号。

Step3 采样复信号互相关时差估计方法测量信号到达两个观察站的到达时间差。通过网格搜索两路复信号间的互相关峰值对应的时延即为两路信号间的相对延迟(到达时间差)。

Step4 将两路信号在时延上对齐(例如，第一路信号较第二路信号延迟了200个样本点，则将第二路信号的前200个样本点丢弃，同时将第一路信号的后200个样本点丢弃，使得后面参与多普勒频差估计的两路信号的起始时刻相同)。

Step5 根据Step 4，重新确定第二路信号的跳频序列。

Step6 根据脉冲周期将两路信号分别存储为矩阵形式，矩阵的每一列表示持续时间长度为一个脉冲周期的信号样本序列。

Step7 跳变沿检测完成符号同步，然后取出有用信号(复观察信号)。

Step8 在Step 3中已经粗略估计了一个频差，在预估频差周围进行两次搜索多普勒频差估计目标函数峰值，使结果更精确，当目标函数取得最大值时即得到双站间的多普勒频差估计结果。

Step9 由多普勒频差计算目标径向速度差。

3 双站多普勒频差估计仿真

为仿真两个固定观测站实现运动目标无源定位的多普勒频差估计性能，假设观测站1的坐标为(0,-10) km，观测站2的坐标为(0,10) km。

设置跳频信号频率范围为1～1.2 GHz，跳频带宽为200 MHz，跳频的频率间隔为5 MHz，随机选取跳频图案产生300个跳频脉冲信号，跳频脉冲持续时间为10 μs，调制方式为MSK，符号率设为5 Mbit/s，瞬时带宽为3.5 MHz。

仿真工具为Matlab 2013，电脑主要配置:Intel(R) Pentium(R) G630 @2.70 GHz CPU，4 GB RAM。

3.1 不同输入脉冲个数下的仿真

该仿真分析算法所使用的脉冲数量与多普勒频差估计性能的关系，并与基于子空间算法进行对比分析。假设目标坐标为(215，24) km，目标的速度向量为(257，86)m/s，通过矢量运算，可以计算得到目标到观测站1的径向速度267.278 6 m/s，目标到观测站2的径向速度为262.045 0 m/s，实际径向速度差为-5.233 5 m/s。设定信噪比为10 dB。

根据上述仿真参数，仿真数据存在41个跳频频点，设置参考载波频率fc为1 GHz，则式(21)的αi取值为(1.000，1.005，1.010，1.015，…，1.200)，按照归一化多普勒频差最大似然估计的9个步骤估计出多普勒频差。图1和图2给出了不同输入脉冲个数下分别进行100次独立试验，通过公式

(27)

得到的多普勒频差估计RMSE，然后比较RMSE及运行时间与所使用的脉冲个数的关系。

仿真基于子空间算法时，分别在每一个跳频频点上估计出对应的多普勒频差，然后由式(22)换算成参考载波频率1 GHz上的频差，可得到41个多普勒频差，取平均值得到最终的参考载波频率多普勒频差估计值。

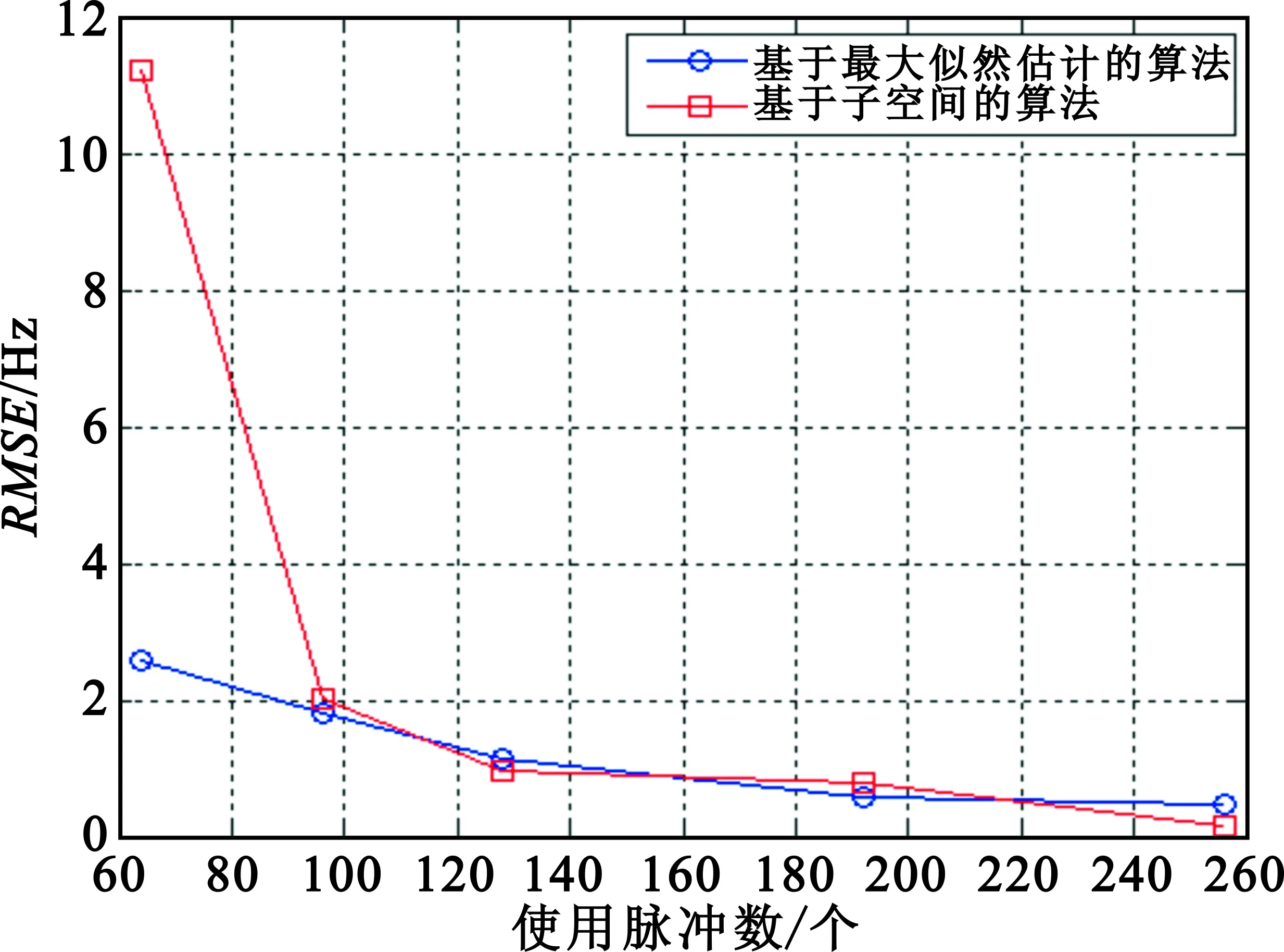
图1 双站下多普勒频差估计均方根误差与脉冲个数间关系Fig.1 The relationships between MSE of Doppler frequency estimation and the number of pulse on double-base situation

从图1中可以得到以下结论：

(1)当所使用的脉冲数越来越多的时候，多普勒频差估计的均方根误差越来越小，这说明脉冲数越多为多普勒频差估计提供的信息量越大；

(2)当脉冲数量较少时(比如少于100个脉冲)，归一化多普勒频差最大似然估计算法好于基于子空间的算法，这主要是式(21)使用了不同跳频频点的所有脉冲信号对参考载波频率上的多普勒频差进行估计，而基于子空间算法是在不同跳频频点上分别估计出相应的多普勒频差，可以认为归一化多普勒频差最大似然估计算法具有全局最优性；

(3)当脉冲数量达到一定数量后(比如200个脉冲)，算法所用脉冲数量的增加对性能的改善不明显，这对实际工程中选取脉冲数量具有指导意义。

图2给出了所提算法与文献[7]中所提算法的效率的比较，可以看出在使用脉冲数量大于200时，所提算法效率逐渐提升，当脉冲数量为240时，效率提升在30%以上。因为文献[7]中所提基于子空间的算法涉及到自相关矩阵的谱分解，会带来较大的计算量，而所提基于最大似然估计的算法避开了这些计算。

图2 所提算法与基于子空间的算法效率比较Fig.2 The efficiency comparison between the proposed algorithm and the subspace algorithm

3.2 不同SNR下的仿真

在不同SNR下分别进行200次独立试验，图3给出了多普勒频差估计RMSE与速度差估计RMSE仿真结果。仿真中采用128个脉冲数据进行一次多普勒测量，观测站位置设置与前面双站仿真案例相同。目标位置坐标(220,30) km，目标速度(-228,-186)m/s，仿真了SNR为[0∶2∶20]dB时的估计精度。

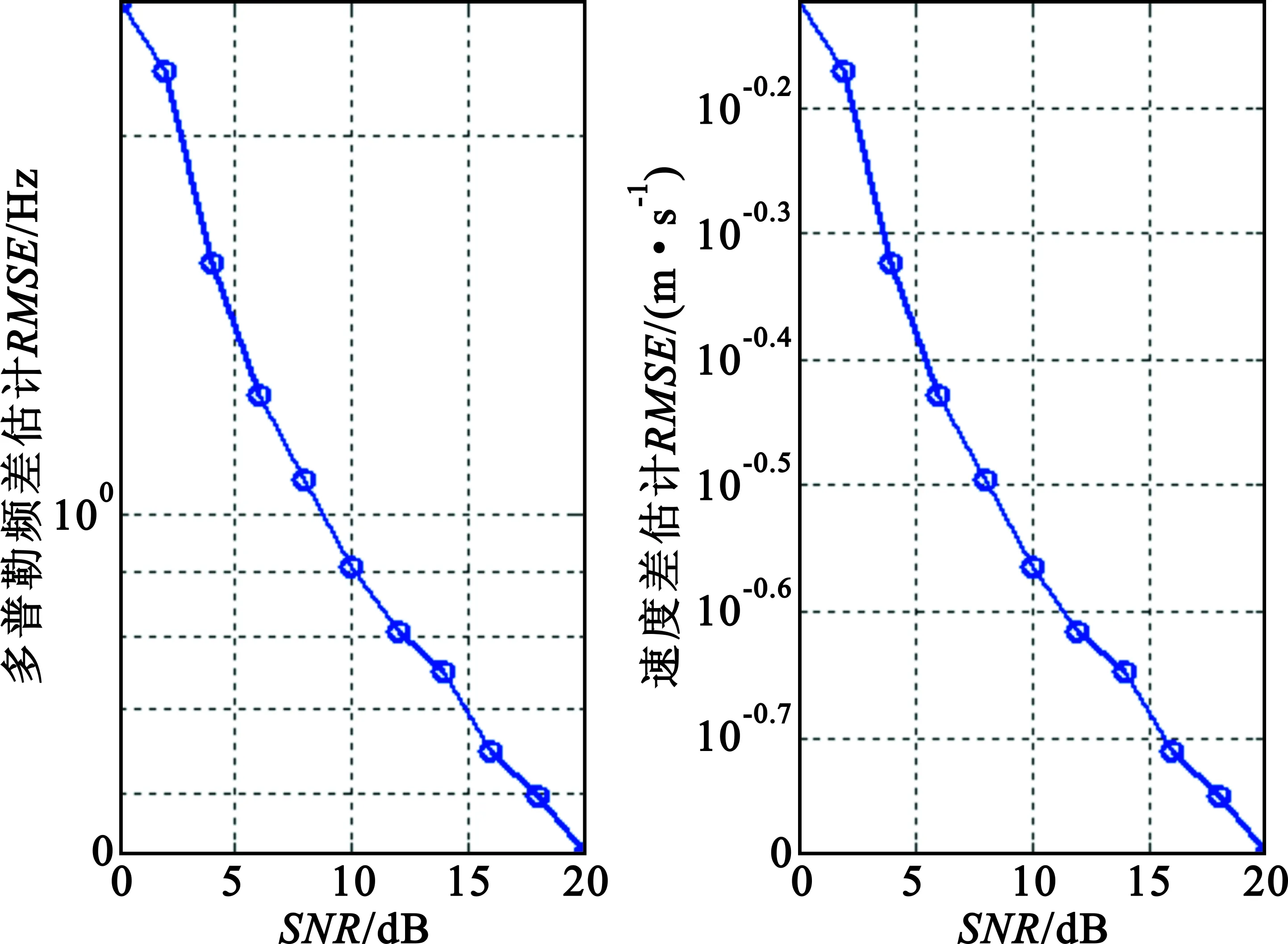
图3 双站下多普勒频差及速度差估计精度与SNR间关系Fig.3 The relationship between the accuracy of Doppler frequency difference estimation and velocity difference estimation and SNR on double-base situation

对于双站仿真，图中仿真结果与预计结果接近，随着SNR的增大，估计的均方根误差越来越小。

4 结束语

本文针对两个观测站估计跳频脉冲信号多普勒频差问题，先构造一个关于FDOA的似然函数，然后用网格搜索的办法找到使似然函数最大的频差。从仿真结果可以看出，这种方法具有很高精度，充分利用了跳频脉冲串中不同频率的多普勒频差信息提高了对速度差的估计性能；随着利用的跳频脉冲数量增多估计性能越高，并且基于这种多轮搜索的算法与基于子空间的算法相比较在使用脉冲数较多时效率提升较为明显。在后续研究中，一方面应考虑对所提算法的实现过程进行进一步优化，提高执行效率；另一方面，在三站以上的多站定位系统中，应研究利用所有接收站的接收信号实现对多个FDOA的估计算法，提升FDOA估计精度用于更精确的目标定位。