基于归一化秩特征的交织类型盲识别

龙 浪 杨俊安 刘 辉 梁宗伟

(1.国防科技大学电子对抗学院，合肥,230037； 2.安徽省电子制约技术重点实验室，合肥,230037)

引 言

在数字通信中，信道编码可以提高通信的可靠性，目前信道编码主要包括线性分组码、RS(Reed-Solomon)码、卷积码和LDPC(Low-density parity-check)码等[1-2]，其中RS码由于具有纠错能力强、编码结构简单的特点，被广泛应用于无线通信、深空通信以及军事通信等各个领域中，例如在通用数据链(Common data link，CDL)系统中就采用RS码作为外编码，然而这种信道编码方式纠正突发错误的效果并不是很明显，因此在数字通信中，通常采用交织技术将经过信道编码后的码元位置进行置换，使信道上的突发错误在时间上扩散成随机错误，从而提高系统抵御突发错误的能力[3-4]，其中分组交织和卷积交织在实际通信系统中应用较为广泛。然而，对于信息对抗方，交织技术增加了编码识别的难度。交织技术一般运用在信道编码之后，若想完成对截获序列编码参数的盲识别并获取所传输信息，就必须先实现交织类型识别及其参数的识别，其中交织类型盲识别是进行交织参数盲识别的前提，是对截获序列作进一步处理的基础，例如，在破译信息对抗方CDL编码参数时，需先对交织器类型进行判断，因此，展开针对RS码的交织类型盲识别，具有一定的现实意义。

从公开发表的文献来看，目前已有的研究多是在已知交织类型的基础上，进行交织参数盲识别[5-11]，关于交织类型识别的文献相对较少。文献[11]中利用帧同步码的累积量峰值位置的个数来区分序列的交织类型，但是缺少进一步的阐述，且该方法需要已知帧同步码等先验信息。文献[12]提出一种针对线性分组码的分组交织器检测方法，但该方法需要已知相关起始位和相关长度等先验信息。文献[13]中提出了一种广义码重分布分析法，以交织序列的实际码重分布与均匀分布之间的欧式距离作为判决准则来进行类型识别，能较快识别出交织类型，但是适用的交织器类型受信号码字长度的限制，且抗误码性能较差。文献[14]中提出了一种利用估计出的交织参数特征逐一判断、依次识别的方法，该方法需要结合盲识别后的交织参数，缺乏可行性。

本文针对常用的分组交织和卷积交织，提出了一种适用于RS码的基于归一化秩特征的交织类型盲识别方法，通过构建分析矩阵，并利用高斯约当(Gauss-jordan elimination through pivoting，GJETP)算法[15]对分析矩阵进行初等变换，从而计算出矩阵的归一化秩，结合分组交织和卷积交织下分析矩阵的归一化秩变化规律，实现交织类型的识别，并通过仿真实验验证了方法的可行性与有效性。

图1 分组交织原理Fig.1 Structure of block interleaver

1 常见的交织类型

1.1 分组交织

当采用分组交织时，其工作原理如图1所示，以交织周期S=Nr×Nc的数据块为单位进行交织，Nr和Nc分别表示交织矩阵的行数和列数，其中Nr=6，Nc=4，输入序列为1到24。分组交织具有同组同块性的典型特征，同一分组码必在同一交织块内，不可能分布在两个数据块中。

1.2 卷积交织

当采用卷积交织时，其工作原理如图2所示，其中B为交织深度即支路数，M为交织宽度即延迟数。与分组交织相比，卷积交织后的码序列不具有分块特性，在一个码字长度范围内既有前一码字中的码元，也有后一码字中的码元，即交织后的序列具有前后交联性[16]，且在任意长度的码字分组块内都不只含若干个完整的码字集合，并将按照这样的特点循环下去。

图2 卷积交织原理Fig.2 Structure of convolutional interleaver and de-interleaver

2 交织类型盲识别

RS码在实际通信系统中是以二进制码流进行传输的，参数为(nc,k,m)的RS码序列可看做是伽罗华域(Galois felid，GF)GF(2m)上的码元在GF(2)上映射得到的二进制(mnc,mk)线性分组码[17]，其中nc为码长，k为信息长度，m为码字宽度，因而可利用基于线性分组码的交织类型盲识别方法来实现对RS码的交织类型盲识别。

图3 秩缺与满秩Fig.3 Deficient rank and full rank

2.1 分析矩阵

将截获到的编码交织序列，按行排列成一个r行b列的矩阵A，同时设置初始搜索周期bmin和终止搜索周期bmax，b的取值遍历区间[bmin，bmax]，假设序列长度为L，则有r=[L/b]，其中[·]表示向下取整，且r≫b。当每行中含有t组完整码字，且对齐正确时，如图3(a)所示，则根据线性分组码的特点：同一码组内的校验码元和信息码元具有线性相关性，当对矩阵A进行列变换后，分析矩阵将会出现秩的缺失；反之，若没有对齐，如图3(b)所示，则分析矩阵将不会出现秩的缺失，为满秩矩阵。本文中将校验码元所在的列称为“相关列”，信息码元所在的列称为“独立列”。

2.2 归一化秩特征法

当选取的列数为bx时，每行中含有多组完整码字，且对齐正确，此时分析矩阵A会出现秩的缺失，令此时矩阵的秩为ρ，在不考虑误码的情况下，利用伽罗华域上的GJETP算法[15]对矩阵A进行初等变换化成下三角矩阵Q，如式(1)所示。

(1)

式中ai,j(2≤i≤r,1≤j≤ρ)表示矩阵元素，可取1或0。但由于在实际传输中可能存在误码，分析矩阵A可能不会出现秩缺或者只有1～2个列数有降秩，无法准确地确定独立列所在的位置，从而无法直接通过初等变换来获得秩的大小。观察发现，在误码的情况下，经过变换的分析矩阵中相关列比独立列含有更多的“0”，可以定义每列中0的个数所占的比例为零值比φ，如式(2)所示，通过φ与预先设定的门限值Tth的比较即可判断该列是否为独立列，从而来获得矩阵秩的大小。

(2)

其中φ(c)表示第c列中0的个数。

为实现分组交织和卷积交织的类型识别，定义分析矩阵中独立列所占的比例为归一化秩p，即

(3)

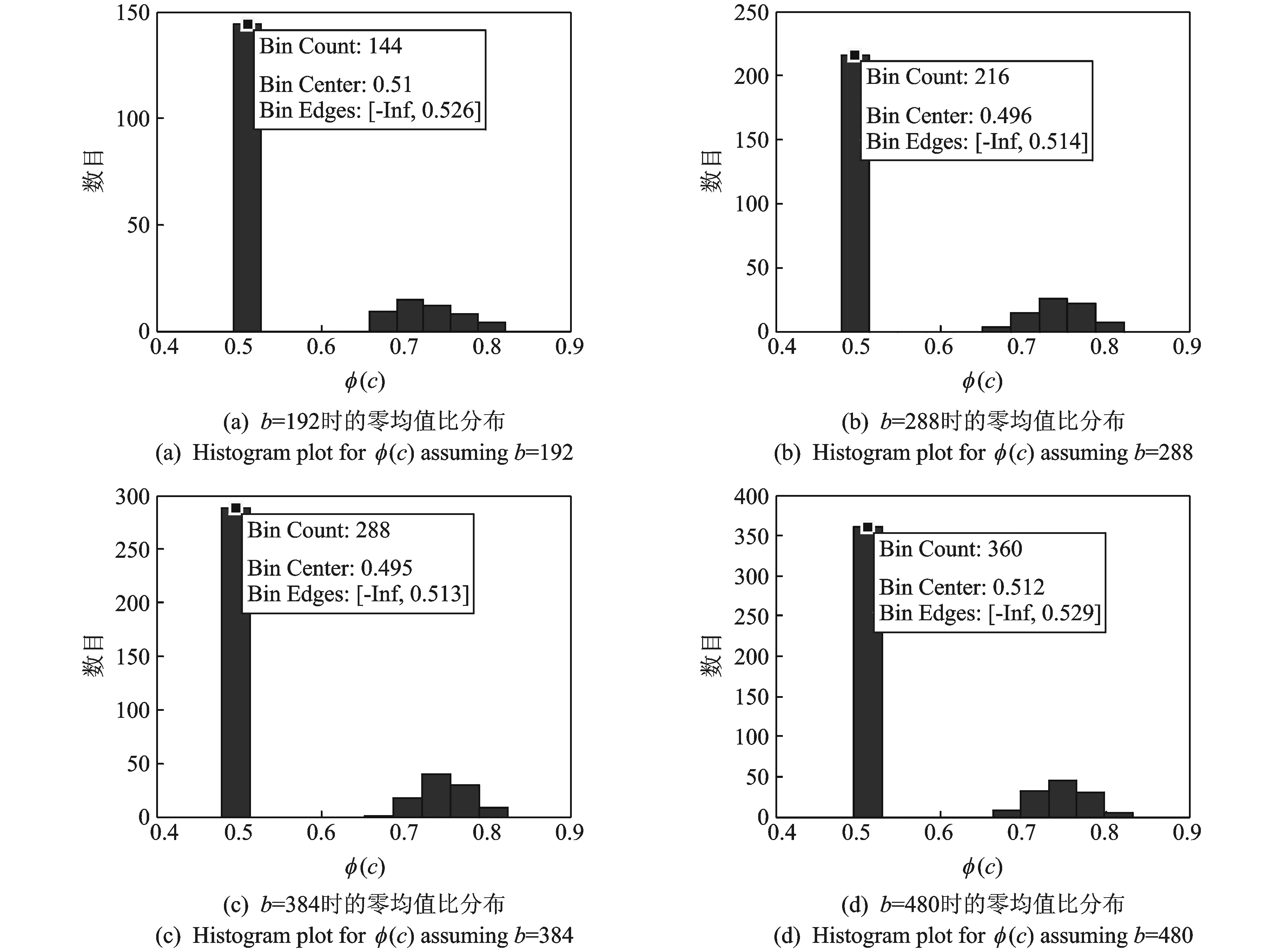
其中N(b)=card(c∈1,2,…,b|φ(c)

(1) 当截获数据的交织类型为分组交织时，在不需要考虑交织周期S和等价码长mnc的倍数关系的情况下，只要当列数b满足式(4)时，分析矩阵中各行的码字就能保持对齐，此时由于校验码元与信息码元之间的线性相关性，分析矩阵就会出现秩缺失的情况；其他情况下，矩阵A均为满秩，即p=1。

b=βlcm(mnc,S)=βζ×mnc

(4)

式中：β，ζ为正整数(β,ζ=1,2,3,…)；lcm(mnc，S)表示mnc与S的最小公倍数。

根据分组交织的性质可知，每行含有βζ个完整码字，通过计算可得矩阵的归一化秩如式(5)所示，为一个常数，与矩阵列数b无关，即有

p=rank(A)/b=βζmk/b=βζmk/βζmnc=k/nc

(5)

(2) 当截获数据的交织类型为卷积交织时，同理可知，只要当列数b满足式(6)时，分析矩阵就会出现秩缺失的情况；其他情况下，矩阵A均为满秩，即p=1。

b=κlcm(mnc,B)=κη×mnc

(6)

式中κ，η为正整数(κ,η=1,2,3,…)。

根据卷积交织的性质可知，每行至少含有λ(λ<κη)个完整码字，计算可得此时矩阵的归一化秩为

p=rank(A)/b=λmk+(mnc(κη-λ))/κηmnc=λk+nc(κη-λ)/κηnc

(7)

式中κ，λ为随b的变化而变化的量，故卷积交织下，矩阵的归一化秩随着分析矩阵的列数的变化而变化。

为了研究分组交织和卷积交织下矩阵的归一化秩随列数b的变化规律，首先假设b=κlcm(mnc,B)和b′=(κ+1)lcm(mnc,B)是连续出现秩缺失的分析矩阵所对应的列数，此时，分组交织下秩缺矩阵的归一化秩皆为k/nc，保持不变；而卷积交织下秩缺矩阵的归一化秩分别如式(8，9)所示。

p=λk+nc(κη-λ)/κηnc

(8)

p′=(λ+η)k+nc[(κ+1)η-(λ+η)]/(κ+1)ηnc=(λ+η)k+nc(κη-λ)/(κ+1)ηnc

(9)

定义两归一化秩的差值为D，则

(10)

由于在卷积交织中，nc>k，κη>λ，且κ,η,nc,λ为正整数，故D<0，即卷积交织中，归一化秩呈现递减的趋势，这样就可以通过观察秩缺矩阵的归一化秩的变化规律来实现交织类型的识别。

综上，交织类型盲识别的判别准则为：当归一化秩相等时，则识别为分组交织；当归一化秩依次递减，则识别为卷积交织。

2.3 算法流程

(1) 将截获到的编码交织数据按行放入r×b的分析矩阵A中，其中b分别取bmin，bmin+1，…，bmax-1，bmax且满足r≫b。

(2) 选定门限值Tth。在无噪时，校验列应为全零列，由于噪声的存在，校验列并不会是全零列，但所含“0”数目大于“1”的数目，因此，一般选取Tth>0.5来区分校验列与独立列。

(3) 在无噪情况下直接求归一化秩，观察存在秩缺失时的归一化秩变化规律；在有噪环境下，利用GJETP算法将矩阵A转换为下三角矩阵Q，并根据设定的门限值Tth计算N(b)来求解归一化秩，同样观察存在秩缺失时的归一化秩变化规律。

(4) 当存在秩缺失时，若归一化秩相等，则识别为分组交织；若归一化秩依次递减，则识别为卷积交织。

3 实验仿真与性能分析

3.1 实验仿真与结果

仿真数据采用(8，6，4)RS码，在信道误码率(Bit error rate,BER)为0.02的条件下分别对交织深度B为3、交织宽度M为16的卷积交织和Nr=3，Nc=16的分组交织进行交织类型识别，其门限值Tth选取为0.55。

当分析矩阵的列数分别为192，288，384和480时，卷积交织和分组交织下的分析矩阵经初等变换后均会出现秩的缺失，此时秩缺矩阵中各列的φ值分别如图4和图5所示，从图中可知，当门限值Tth为0.55时，可以通过各列的φ值与门限值的比较，来判断该列是否为独立列，从而根据式(3)计算出对应的归一化秩，分别如表1和表2所示。

图4 卷积交织下不同列数的零均值比分布Fig.4 Histogram plot for φ(c) considering convolutional interleaver

图5 分组交织下的不同列数的零均值比分布Fig.5 Histogram plot for φ(c) considering block interleaver

列数b独立列数目N(b)归一化秩p1921610.838 542882330.809 033843050.794 274803770.785 42

表2 BER=0.02时分组交织的归一化秩

不同列数下的分析矩阵归一化秩变化规律如图6和图7所示。从图6中可以看出，当RS码卷积交织序列在列数为等价码长和交织深度的倍数处出现秩缺失，即图中的192，288，384和480处，同理论分析b=κlcm(mnc,B)=κlcm(32,3)=96κ保持一致，且秩缺矩阵的归一化秩由0.838 54依次递减为0.785 42；而图7中的结果表明：RS码分组交织序列也在同样的列数处出现秩缺失，且秩缺矩阵的归一化秩保持不变，皆为0.75，因此，根据秩缺矩阵归一化秩的变化规律就可以有效实现对截获序列的交织类型的判决。

图6 卷积交织下的归一化秩特征Fig.6 Normalized rank for convolutional interleaver

图7 分组交织下的归一化秩特征Fig.7 Normalized rank for block interleaver

图8 在不同参数下的识别性能分析Fig.8 Comparison of recognition performance among different parameters

3.2 识别性能对比分析

3.2.1 门限值选取

为了进一步确定门限值的选取标准，对本文算法在不同误码率条件下，分别取不同门限值Tth时的成功识别概率进行了蒙特卡洛仿真，每种误码率条件下对每个门限值进行1 000次试验，记录能够成功识别出来的次数，仿真结果如图8所示。从图中可以观察到随着Tth的变化，成功识别出交织类型的概率也会随之变化，在误码率0.02到误码率0.06变化范围内，随之误码率的不断增大，能正确识别的门限值范围在不断减小，当误码率为0.06时，门限值取0.57下的识别正确率最高。

3.2.2 抗误码性能对比

为了更好地验证算法的容错性，信道误码率取0.01到0.1，并针对不同的编码和交织参数组合进行1 000次蒙特卡洛实验。表3显示了采用(7,3,3)RS码，Nr=7,Nc=4的分组交织和B=5,M=3卷积交织时的识别正确率及仿真结果；表4显示了采用(31,11,5)RS码，Nr=5,Nc=9的分组交织和B=7,M=6卷积交织时的识别正确率及仿真结果。由表3和表4可以看出，当信道误码率小于0.03时，交织类型的识别准确率在98%以上；当信道误码率低于0.04时，交织类型的识别准确率在80%以上，表明了该识别方法的容错性能较好。

表3 (7,3,3)RS码，Nr=7,Nc=4的分组交织和B=5,M=3卷积交织识别结果

表4 (31,11,5)RS码，Nr=5,Nc=9的分组交织和B=7,M=6卷积交织识别结果

图9 3种算法误码性能分析Fig.9 Comparison of recognition performance among different three algorithms

图9给出了本文算法、广义码重分布分析算法[13]以及逐一判断法[14]在不同误码率情况下的识别正确概率，并在表5记录完成一次正确识别所需的运行时间。从图中可以看出，广义码重分布分析算法和逐一判断法随着误码率的增加，算法性能急剧下降，当误码超过0.04时，广义码重分布分析算法识别率下降到50%以下，而逐一判断法的识别率已不能正确识别出参数类型，但本文中提出的算法的识别概率仍高于80%，能较好地进行识别，因此本文算法具有良好的抗误码性能。但从表5中可以看出，本文算法在计算时间上要稍逊于广义码重分布分析算法，算法复杂度较高。这是由于广义码重分布分析算法不需要对矩阵进行多次行列变换，减少了运行时间，但是该方法只能对在分组码长恰好等于交织深度与交织宽度的乘积时的交织类型进行识别，在非合作通信中，由于缺少先验信息，方法具有较大局限性。本文所提出的算法可以较好地完成对系统交织类型的识别。

表5 不同算法的运行时间对比

4 结束语

本文针对RS码，提出了一种基于归一化秩特征的交织类型盲识别方法，在不需要考虑码长约束的条件下，通过高斯约当算法对分析矩阵做初等变换，结合所得下三角阵中各列的零值比计算出秩缺矩阵的归一化秩，最后利用归一化秩的变化规律完成交织器类型盲识别，较以往的识别方法相比，本文识别方法不需要任何先验条件，弥补了以往交织类型识别方法的不足。仿真实验结果表明，本文所提方法可以较好地完成交织类型识别，且具有良好的抗误码能力，在误码率为0.04时，仍能够保证较高的识别正确概率，并通过不同门限值下的系统性能比较，确定了识别算法的最优门限值为0.57，可为实际的工程应用提供一些参考。