长期循环荷载作用下粉质黏土动力特性及相关模型修正

，

(三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 443000)

1 研究背景

建设在软土地基上的高速公路、高速铁路、地铁等交通工程，在交通荷载的持续作用下，路基会发生工后沉降[1]。交通荷载具有持续时间长、作用周期有一定规律性的特点，使之区别于静力荷载和地震荷载。目前国内外学者针对土体在循环荷载作用下的动力特性进行一系列的研究，并取得了丰硕的成果。

在土体动应变特性研究方面，曹洋等[2]、闫春岭等[3]认为振动荷载频率越低，动应变发展越迅速，而Yasuharak等[4]和刘飞禹等[5]研究发现频率对动应变的影响程度较低。Allen[6]、李剑等[7]研究了不同围压下动变形的发展规律，其中后者发现在小剪应变条件下，随着围压的增大，红黏土动剪切模量与动剪应变的关系曲线逐渐趋于“直线”关系。也有较多学者根据不同循环荷载条件下的试验成果，建立了描述土体累积变形的模型[8-11]。

在土体动孔压特性研究方面，黄博等[12]、丁智等[13]采用不同波形模拟列车荷载下软黏土的孔压特性。同为不排水条件下，前者发现正弦波作用时试样产生的残余孔压远大于半正弦波和模拟高速列车荷载的不规则波，且半正弦波和不规则波在相近动应力比作用下产生的残余孔压也相近，而后者发现偏压正弦波比矩形波、三角形波以及正弦波效果更好。陈颖平等[14]针对水泥土样与原状土样及重塑土样进行动三轴试验发现，3种试样在振动初期动孔压变化规律类似，但水泥土样最终的动孔压值会偏高一些，且接近或大于固结压力。

上述研究发现在对土的动力特性研究中，考虑到应力循环次数较小，并不能反映出交通荷载的长期性。因此，本文对饱和粉质黏土长达20 000次的循环振动，所得研究成果可以为实际工程提供参考依据。

2 试验设备与试样制备

2.1 试验设备

本研究采用SDT-10型微机控制土动三轴试验机，该设备有2个高精度控制器能够分别控制围压和轴向压力的振动幅值；压力采用液压控制，油源最大可以提供21 MPa的压力。控制系统可以根据试验需要设置不同的振动波形(正弦波、锯齿波、三角波等)，频率范围为0～5 Hz。该仪器可用于不同种类土的动强度试验，也可根据实际需要设置振动剪切时的排水条件(排水和不排水)。试验过程中仪器能测量并记录多项数据(轴向力、轴向位移、孔隙水压力、排水量)，据此可确定动弹性模量、阻尼比、动孔压等动力特性指标。

2.2 试样制备

本研究所用土样为黄褐色粉质黏土。对土样进行基本物理性质试验，测得参数见表1。

表1 土样物理参数Table 1 Physical parameters of soil sample

土样风干后过2 mm筛，测定风干含水率，称取一定质量的干土，根据设定干密度(1.5 g/cm3)和设定含水率(20%)计算出所需水量。土样配好后装入保湿缸闷放24 h使水分均匀，后按照《土工试验规程》(SL 237—1999)中的试验步骤测定实际含水率。本试验重塑样采用分层击实法制备成直径61.8 mm，高120 mm的柱状三轴试样。将制备好的试样放入真空缸中进行抽真空饱和。

2.3 试验方案

置饱和后的土样于仪器压力室，先对试样进行等向固结，固结完成后关闭排水阀，再对试样施加循环荷载进行不排水振动剪切试验，荷载波形采用正弦波。

土体在受迫振动过程中应变发展滞后于应力变化，形成了环状滞回圈。图1为应力-应变滞回曲线，其中峰值对应的应变和偏应力分别为最大动应变εNmax和最大偏应力qmax；其谷值对应的应变和偏应力分别为塑性应变εNmin和最小偏应力qmin，动弹性模量EN=(qmax-qmin)/(εNmax-εNmin)。qmax与qmin的绝对值大小与振幅σd相等。

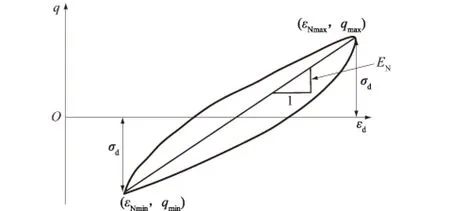
图1 应力-应变滞回圈示意图Fig.1 Stress-strain hysteretic loop

本研究主要控制因素为围压σ3、动应力比H及振动频率f，其中H=σd/σ3。试验共有7组试样，其中1，2，3号试样变化因素为围压σ3;1，4，5号试样的变化因素为动应力比H;1，6，7号试样的变化因素为频率f。具体试验方案见表2。

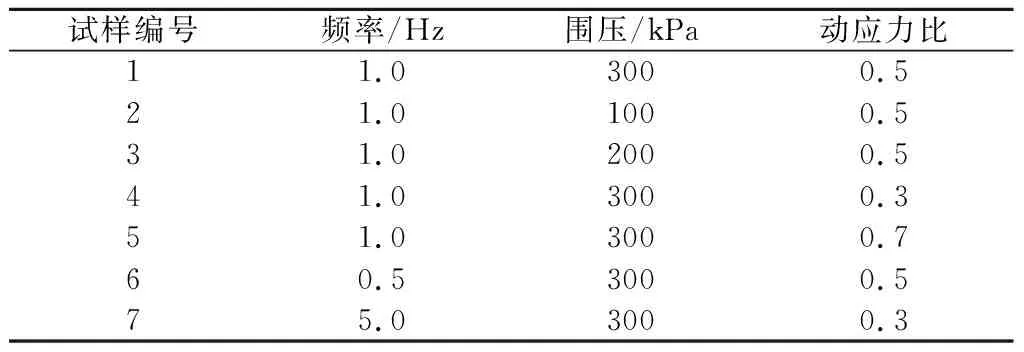
表2 动三轴试验方案Table 2 Schemes of dynamic triaxial test

3 试验结果分析及模型修正

由于试验采集的数据较多，为方便后续处理，选取振次N=1，5，10，20，50，100，200，500，1 000，2 000，5 000，10 000，20 000所对应的数据进行整理计算，得到了各控制因素下的动应变、残余孔压比，然后绘制成图。

3.1 累积塑性应变与振动次数的关系

3.1.1 累积塑性应变随振动次数的变化规律

图2为不同围压、频率以及动应力比下的累积塑性应变εs与lgN的关系曲线。

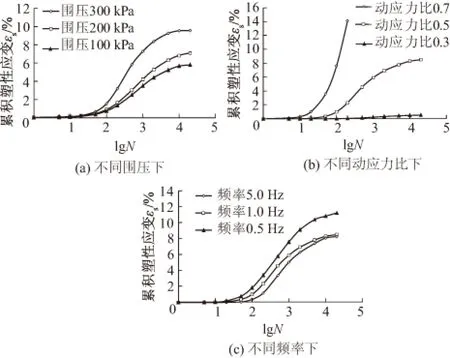
图2 不同条件下试样εs -lgN关系曲线Fig.2 Curves of εs -lgN under different loads

由图2可以看出：

(1)3项荷载条件下累积塑性应变εs随着lgN的增加均呈现出相同发展趋势，即εs随lgN的增加而增加。在振动初期εs随lgN缓慢增长，然后εs增长速率变大，最后曲线逐渐趋于水平。εs-lgN曲线出现上述规律是由于土体自身的塑性决定了试样在被压缩后难以恢复至压缩前的状态，而且随着振动次数的增加累计塑性应变会逐步积累。

(2)当围压不同时，累计塑性变形曲线均呈S型曲线，同一振次下，累计塑性应变随围压的增大而增大。这是由于当围压越小时，土体固结程度越低，孔隙率较大，土体所含孔隙水较多，所以土体承受压力时孔压上升相对较快。根据“动应力比”定义，围压越小时，对应动应力越小，所以当孔压上升相对较快时，有效应力较小，实际作用在土骨架上的应力较小，塑性应变积累相对较慢。

(3)当动应力比不同时，动应力比较大的曲线一直处于动应力比较小的曲线上方。根据“动应力比”定义，当围压相同时，动应力比越大，振动幅值越大，土体所受轴向应力越大。当动应力比为0.7时，曲线呈J型增长；动应力比为0.3和0.5时曲线呈S型。

(4)当振动频率不同时，动应变随着频率的增高而减小。这是由于在围圧和动应力比相同的情况下，土体固结程度和动应力大小相同；当土体承受较高频率的循环荷载时，土体中的孔隙水来不及排出，此时土体所受剪切力等于总应力，在受到相同大小的动应力时，其变形量也较小，变形发展较慢。

3.1.2 累积塑性应变模型改进

生态学中种群增长模型用来描述种群数量在一定条件下随时间的发展规律。在食物匮乏、空间有限、斗争激烈的条件下种群数量呈S型增长模式，其表达式为

M=F/(1+ea-bt) 。

(1)

式中：M为种群数量；F为种群数上限；a，b均为参数；t为时间。

借鉴生物种群增长模型进行改进，得到累积塑性应变εs关于lgN的S型模型，表达式为

εs=h/(1+Gsi-jlgN) 。

(2)

式中：Gs为相对密度，根据表1取Gs=2.74；h，i，j均为拟合参数。

当动应力水平较高时，应变急剧增长，应变ε-lgN曲线形态为J型曲线，Monismith等[15]据此提出了指数模型，即ε=ANB，其中A，B均为拟合参数。

将上述指数模型改进后得到累积塑性应变εs关于lgN的J型模型，其表达式为

εs=k(lgN)m。

(3)

式中k，m均为拟合参数。

在First Optimization数学优化分析软件中采用式(2)对图2中S型εs-lgN曲线进行拟合，可以得到拟合参数h，i，j在3种不同荷载条件下的拟合值。同理，在First Optimization数学优化分析软件中采用式(3)对图3中的J型εs-lgN曲线进行拟合，得到拟合参数k，m在动应力比为0.7时的拟合值。将拟合参数h，i，j，k，m整理成表3。

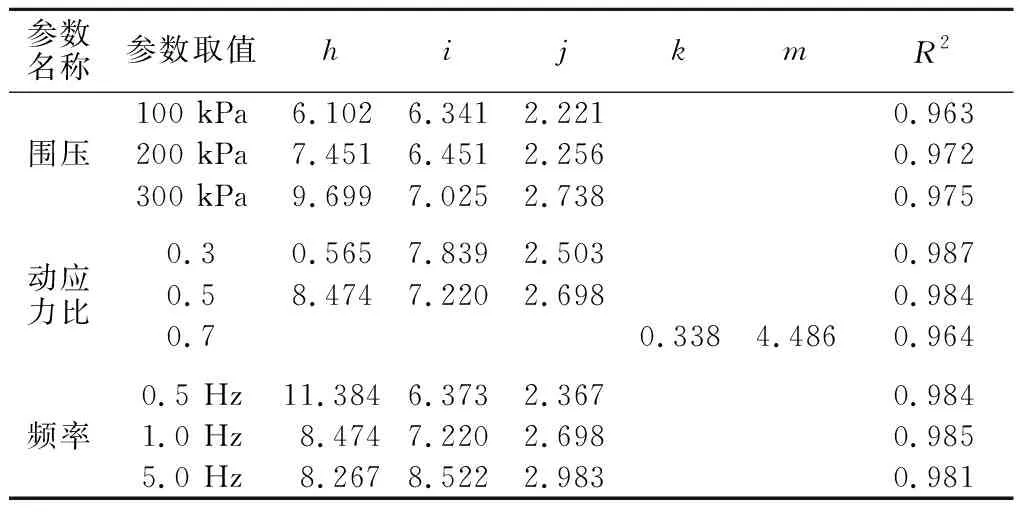
表3 不同荷载条件下模型拟合参数Table 3 Fitting parameters of model underdifferent loads

从表3可以看出：

(1)围压σ3对参数h，i，j的影响，即

(4)

(2)频率f对参数h，i，j的影响，即

(5)

(3)R2均>0.9，2种改进模型能较好拟合3种不同荷载条件下累计塑性应变随lgN的发展规律。

图3为不同动应力比下εs-lgN实际曲线与拟合曲线对比，可明显看出S型曲线和J型曲线改进模型均能很好地模拟累积塑性应变εs随lgN的变化规律。

图3 不同动应力比下εs-lgN实际曲线与拟合曲线对比Fig.3 Fitted curves and actual curves ofεs-lgN under varying dynamic stress ratio

3.2 残余孔压比与振动次数的关系

3.2.1 残余孔压比随振动次数的变化规律

由于振动试验过程中关闭了排水阀门，在围压和轴压的共同作用下，土体内部孔隙水无法排出，此时就会产生孔隙水压力。当围压不相同时，孔压大小不能反映围压对孔压发展的影响程度。为方便研究不同围圧下残余孔压的发展规律，本研究采用定义残余孔压比R对残余孔压孔压进行归一化，其中R=uc/σ3，uc为残余孔压。

图4为不同围压、动应力比、频率条件下的R-N曲线。

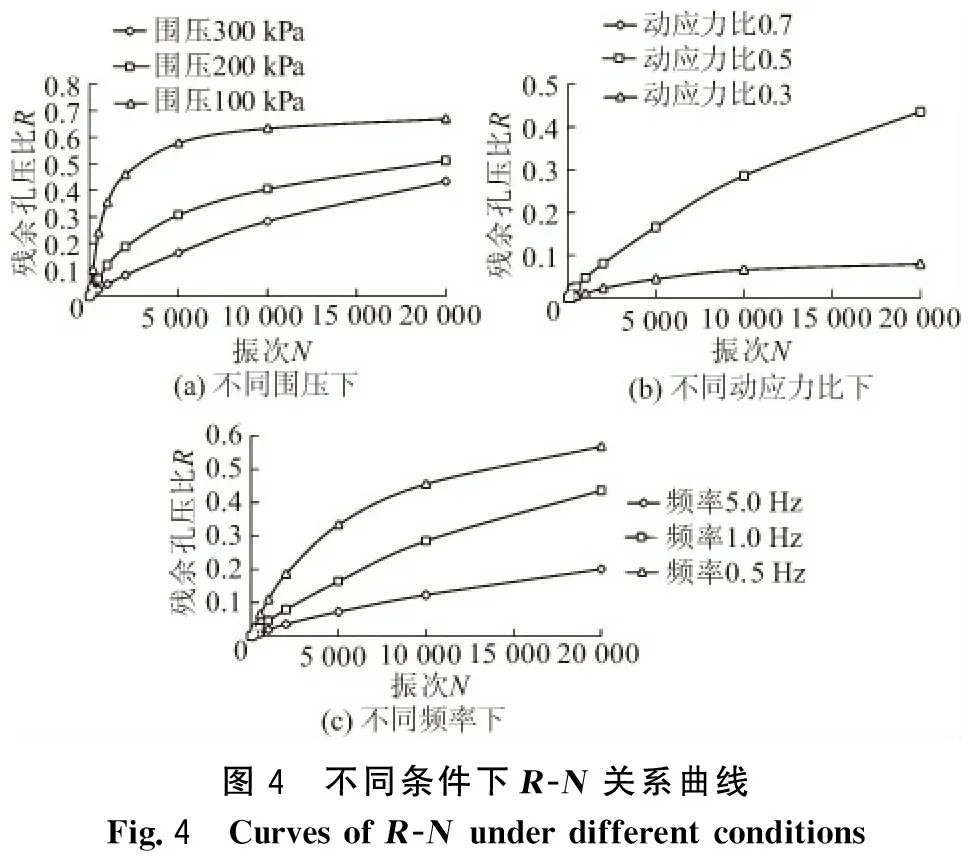
图4 不同条件下R-N关系曲线Fig.4 Curves of R-N under different conditions

由图4可以看出：

(1)在图4中，R-N关系曲线发展趋势相同，R随N的增大而增加。循环荷载的加载波形为正弦波，一个振动周期内土体受力状态可分为2种情况，即当轴向力由谷值增长至峰值过程中土体呈压缩状态，随后轴向力由峰值向谷值回落，此过程中土体相当于被拉伸。当土体受力状态由“压缩”状态进入“拉伸”状态时，由于土体具备一定弹性，土体开始缓慢回弹，孔压也随之缓慢消散。但由于振动频率远远大于孔压消散速度，导致在随后的振动过程中孔压来不及消散而不断升高。

(2)当围压不同时，3条R-N曲线形态相似，均是先快速呈直线增长，然后增长速度变慢，曲线开始向右弯曲，最后缓慢趋于水平。这是由于当围圧较低时，土体固结程度较低，土体孔隙率较大，试样所含孔隙水总量较多，故土体在初始阶段孔压以直线形式迅速上升，当土体内部结构趋于稳定后，孔压增长速率降低。

(3)动应力比为0.3时曲线在N=5 000次时趋于稳定，动应力比为0.5时N<10 000阶段内几乎呈直线增长，然后曲线增长速率变慢，曲线开始向右弯曲。根据“动应力比”定义，围圧相同时，动应力比越大，土体所受动应力越大。在高水平的动应力作用下，土体结构迅速破坏，所以动应力比为0.7时，从图3中可以发现在N=100时，试样就达到破坏，残余孔压积累量少。

(4)当频率为0.5 Hz和1.0 Hz时，R随着N的增大呈直线缓慢增长。当频率较低时土体内部的大部分孔隙水有足够时间转移，随着振动的持续孔压缓慢上升。而频率为5.0 Hz时，残余孔压比先快速呈直线增长，然后增长速度变慢，曲线开始向右弯曲，最后缓慢趋于水平。由于频率高，孔隙水无法及时转移，孔压上升相对较快。

3.2.2 残余孔压比模型改进

在等向固结的条件下，Seed根据饱和砂土等向固结不排水动三轴试验的结果，提出了孔压u随振次N的变化关系[16]，即

(6)

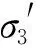
将Seed孔压模型改进为适用于黏土的残余孔压比模型，即

R=[2/arcsin(αN/Ne)-β]/π 。

(7)

式中：Ne为试验结束时的振动次数，取Ne=20 000；α，β均为试验常数。

在First Optimization数学优化分析软件中采用式(7)对图4中R-N曲线进行拟合，可以得到拟合参数α，β在3种不同荷载条件下的拟合值(表4)。

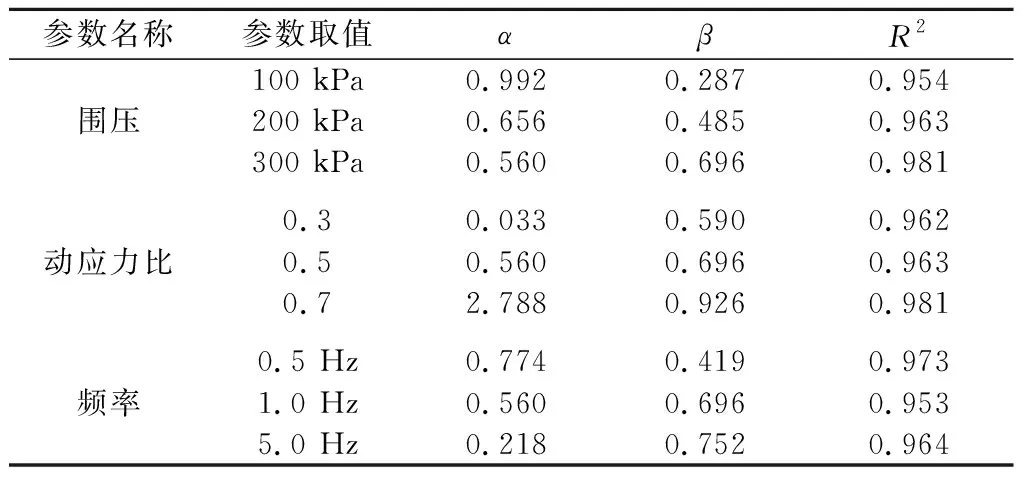
表4 不同荷载条件下模型拟合参数Table 4 Fitting parameters of model underdifferent conditions

从表4中可以得到：

(1)围压σ3对参数α，β的影响，即

(8)

(2)动应力比H对参数α，β的影响，即

(9)

(3)频率f对参数α，β的影响，即

(10)

(4)R2的结果表明改进模型能较好拟合3种不同荷载条件下残余孔压比R随振次N的变化规律。

图5为不同频率下R-N实际曲线与拟合曲线对比，明显可以看出改进模型能很好地模拟残余孔压比R随振次N的变化规律，频率越高，拟合度越高。

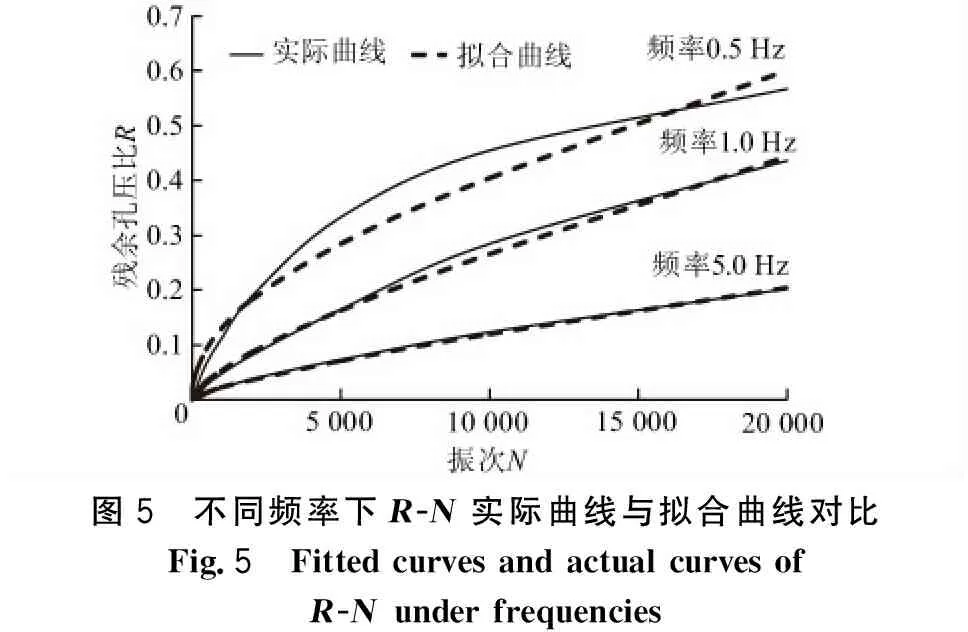
图5 不同频率下R-N实际曲线与拟合曲线对比Fig.5 Fitted curves and actual curves ofR-N under frequencies

4 结 论

本文进行了饱和粉质黏土的动三轴试验，分别就不同围压、动应力比、频率3种荷载条件下累计塑性应变、残余孔压比的变化规律进行了简要分析，得到以下结论：

(1)塑性应变在动荷载作用下逐渐累积，在振次相同时围压、动应力比越大，塑性应变累积值越大，而振动频率越大塑性应变累积值越小。

(2)改进后的种群增长模型能很好地模拟在不同围压、动应力比、频率条件下累积塑性应变εs随lgN呈S型增长的规律。

(3)当动应力比较大时，改进后的指数模型能较好预测εs随lgN呈J型增长的规律。

(4)残余孔压比在动荷载作用下逐渐积累，在同一振次下残余孔压比随动应力比、振动频率的增大而增大，随围压的增大而降低。

(5)改进后的Seed孔压模型能很好地模拟在不同围压、动应力比、频率条件下残余孔压比随振次的变化规律。