基于小波分解及Arima误差修正的径流预测模型及应用
2018-12-19,,,
,,,
(1.国际小水电中心, 杭州 310002;2.河海大学 水利水电学院, 南京 210098)
1 研究背景
径流预测对水电站的运行和水库调度都有着重要意义。由于受气候、流域自然地理和人类活动等因素的综合影响,河道径流变化规律错综复杂,常常表现出多时间尺度性、随机性、突变性以及非线性等特点。因此,径流预测一直是国内外研究的热点和难点。
目前应用于径流预测的常用模型多种多样,主要有人工神经网络、逐步回归、灰色预测、相关向量机(RVM)、支持向量机(SVM)等。 Jain等[1]首次将人工神经网络应用在水库入库流量预测及水库运行方面,并将人工神经网络模型和自回归滑动平均模型进行了比较。左卫兵等[2]在贝叶斯框架下利用相关向量机对黄河某水文站径流进行了预测分析。周秀平等[3]建立了基于支持向量机的径流预测模型并应用于西江流域径流预测中。
各类传统径流预测模型在一定程度上降低了径流预测的难度,尤其对于普通径流时间序列,各常规预测模型均取得较好的预测效果。但是,当径流时间序列中出现多处突变,表现出较强随机性、非线性特点时,上述预测模型的预测结果与实测值误差出入较大,无法达到更高的精确度。
针对目前常用径流预测模型对随机性时间序列的预测能力不强的不足,本文将小波分解法[4]引入到径流预测模型中。对原始径流时间序列进行小波分解和重构,将非平稳的径流时间序列平稳化后,再应用预测模型对其进行预测。针对突变数据对预测结果仍存在一定影响,利用Arima模型对误差进行预测,进一步修正预测值。综合小波分解法、RVM预测模型以及Arima误差修正模型,本文提出了一种基于小波分解法及Arima误差修正的径流预测模型。
2 径流预测模型
2.1 小波分解及重构方法
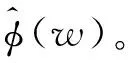
小波分解及重构以多分辨分析为理论基础,于1988年由Mallat首次提出。它的基本思想是以尺度空间Vj和小波空间Wj来表示L2(R)。定义{Vj}j∈Z是L2(R)上的一列闭子空间,小波空间Wj是Vj+1与Vj之差,即Vj+1=Vj⨁Wj,则可以推得
(1)
在此基础上,Mallat提出一种快速小波变换方法[5],包括分解算法与重构算法。
分解算法为
cj+1=Hcj,dj+1=Gcj;
j=0,1,…,J。
(2)
重构算法为
(3)
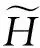
通过上述算法,即可将非平稳的时间序列分解为若干不同尺度下的平稳时间序列。
2.2 相关向量机基本理论
tn=y(xn;w)+εn。
(4)
式中y(xn;w)为中间变量。
y(x;w)可表示为
(5)
式中:w为参数向量;ωn为权重;K(x,xn)为核函数;N为样本数。
假定tn独立分布,则似然函数可表示为
式中:t为目标向量,t=(t1,t2,…,tN)T;w=(ω0,ω1,…,ωN)T;Φ为基函数,Φ=[φ(x1),φ(x2),…,φ(xN)];φ(xn)=[1,K(xn,x1),K(xn,x2),…,K(xn,xN)]T。
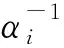
(7)
式中α为超参数,决定权值先验分布[7]。
设α与σ2均服从Gamma先验概率,则有:
(8)
p(σ2)=Gamma(σ2|c,d) 。
(9)

依据似然分布和先验分布的定义,得到w的后验分布为
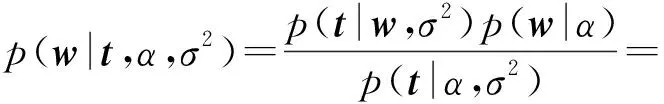
(10)
其中:∑=(σ-2ΦTΦ+A)-1;μ=σ-2∑ΦTt;A=diag(α0,α1,…,αN)。
式中:∑为后验协方差;μ为后验均值;M为相关向量机的数量。
式(10)对w积分可得由超参数α和σ2决定的边缘分布,即
式中:Ω为中间变量,Ω=σ2I+ΦA-1ΦT,I为单位向量。
为简便计算,采用快速序列稀疏贝叶斯学习算法[8]计算超参数和噪声方差。
选用高斯核函数作为模型的核函数,即
K(x,xi)=exp(-g‖x-xi‖2) 。
(12)
式中g为核参数。
为弥补粒子群算法易陷入局部最优的缺陷,采用改进粒子群算法[9]进行核函数全局寻优。
2.3 Arima误差修正
通过RVM模型拟合值与实测值对比,可得到误差序列,将其视作随机时间序列并利用Arima模型[10]进行误差修正,大大提高预测精度。Arima模型可表示为
(13)
式中:φm(m=1,2,…,p)为自回归模型系数;θj(j=1,2,…,q)为均滑动模型系数;p为自回归阶数;q为滑动平均部分的阶数;at为白噪声序列。
进行Arima模型误差修正时,首先确定p和q值,再利用最小二乘法确定其他未知参数,接着拟合误差序列并得到残差序列,判断残差序列是否为白噪声的一个子序列,若是,则通过;若不是,则对参数进行修正,直到满足条件为止[11]。
2.4 径流预测模型
结合小波分解法、RVM模型以及Arima误差修正模型的优点,建立径流预测模型,对非平稳、随机性的径流时间序列进行准确预测,具体步骤为:
(1)利用小波分解法对径流时间序列进行分解,得到若干组子序列,使非平稳、非线性的径流时间序列分解为不同尺度下的平稳时间序列。
(2)对分解出的每一个子序列建立相应的RVM模型,分别进行样本训练、拟合及预测,得到对应每一个子序列的预测结果和残差序列。
(3)对上步中各个子序列的残差序列进行Arima误差修正,通过Arima模型得到对应各个子序列的误差预测值,结合RVM预测结果即可得到子序列的最终预测值。
(4)将所有子序列的预测结果进行小波重构,得到径流时间序列的最终预测结果。
基于小波分解及Arima误差修正的径流预测模型流程图如图1所示。
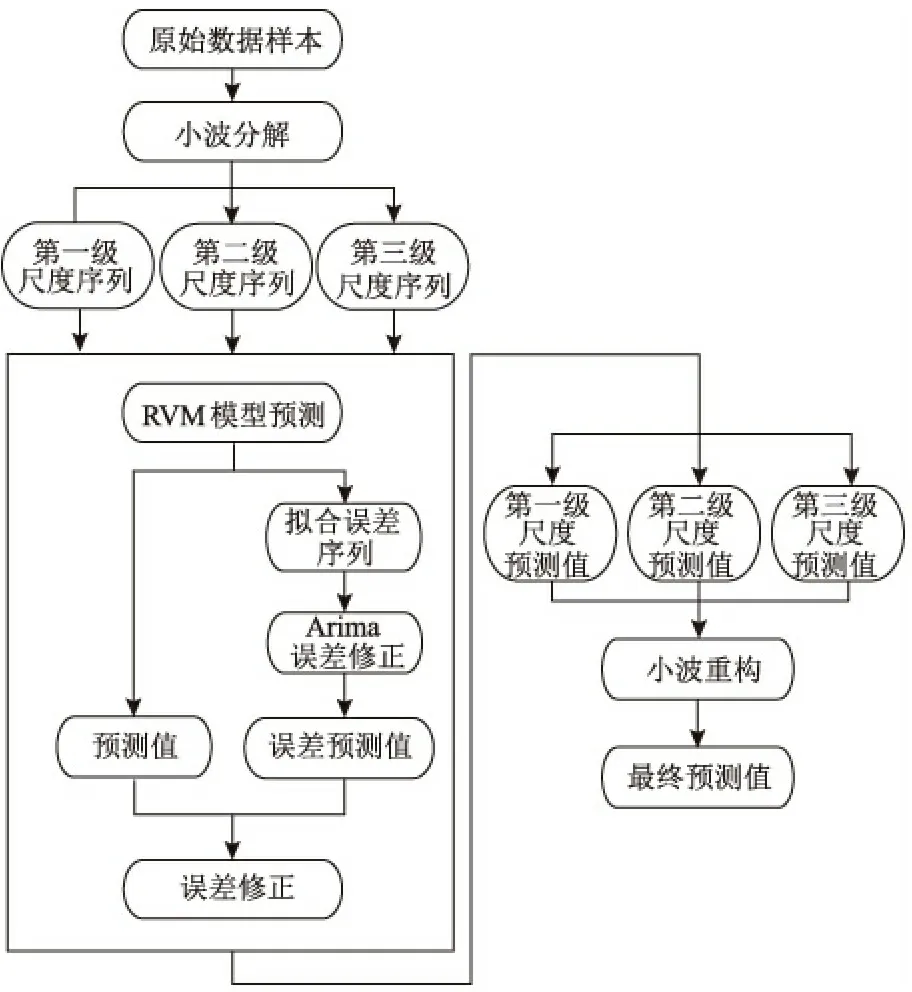
图1径流预测模型流程
Fig.1Flowchartofrunoffpredictionmodel
3 实例应用
浙江省某水电站水库正常蓄水位160.00 m,总库容41.9亿m3,调节库容21.26亿m3。采用基于小波分解及Arima误差修正的径流预测模型对该水电站上游日均流量的监测资料进行分析,抽取2010年2月3日—2011年12月2日监测资料中每间隔3 d为一组,共224组实测资料为样本,前204组用于拟合,后20组用于模型预测。
首先利用小波分解法对数据样本进行预处理,将非平稳、随机性的径流时间序列分解为3组不同尺度下相对稳定的子序列。对应每一个子序列建立RVM预测模型,核参数g的取值范围为[0.01,10];惯性因子ω的取值范围为[0.4,0.8],学习因子c1和c2的范围分别为[1.0,2.5]和[1.5,2.75];核函数的位置因子γ和速度因子υ分别为1.00和0.01。通过RVM模型预测,得出各子序列的预测值以及残差序列,在此基础上,对残差序列进行Arima误差修正,得到误差预测值,进一步修正预测结果。最后对各个子序列的预测结果进行小波重构,得到径流数据样本的最终预测结果。径流预测模型的拟合曲线如图2所示。
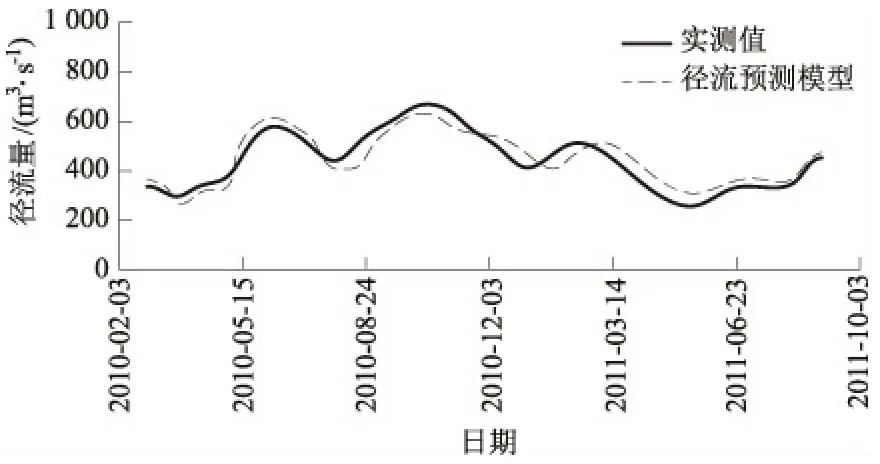
图2径流预测模型拟合曲线
Fig.2Fittedcurveofrunoffprediction
为对比分析,另采用标准的SVM模型、RVM模型对相同数据样本进行预测。3种模型的预测结果对比见表1,预测效果如图3所示。
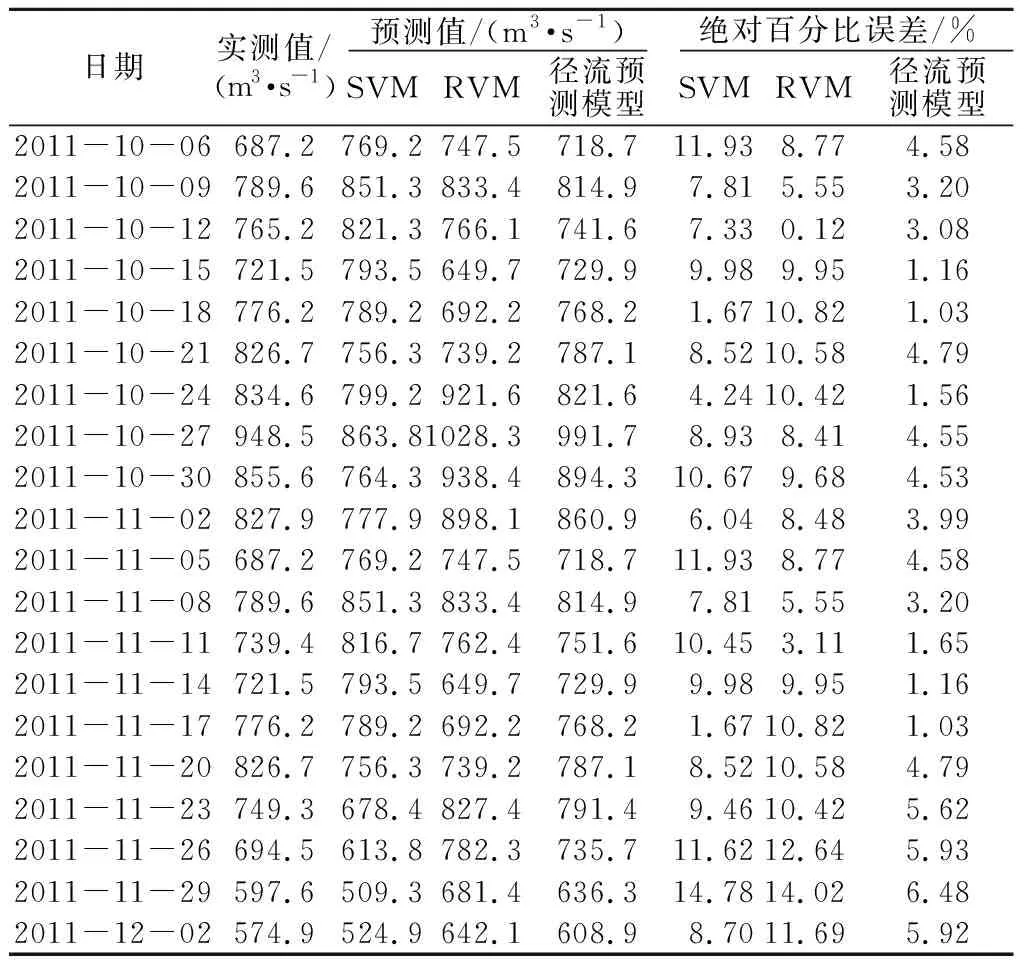
表1 3种模型径流量预测结果对比Table 1 Comparison of prediction results of three models
由表1中数据可知,SVM模型、RVM模型和径流预测模型的预测结果平均残差分别为8.60%,9.02%和3.64%,通过对比,可以发现基于小波分解及Arima误差修正的径流预测模型的预测结果的精度,远高于SVM模型和RVM模型。通过图3中3种模型的预测效果曲线对比,同样可以得此结论,进一步证明了基于小波分解及Arima误差修正的径流预测模型可以提高预测精度。
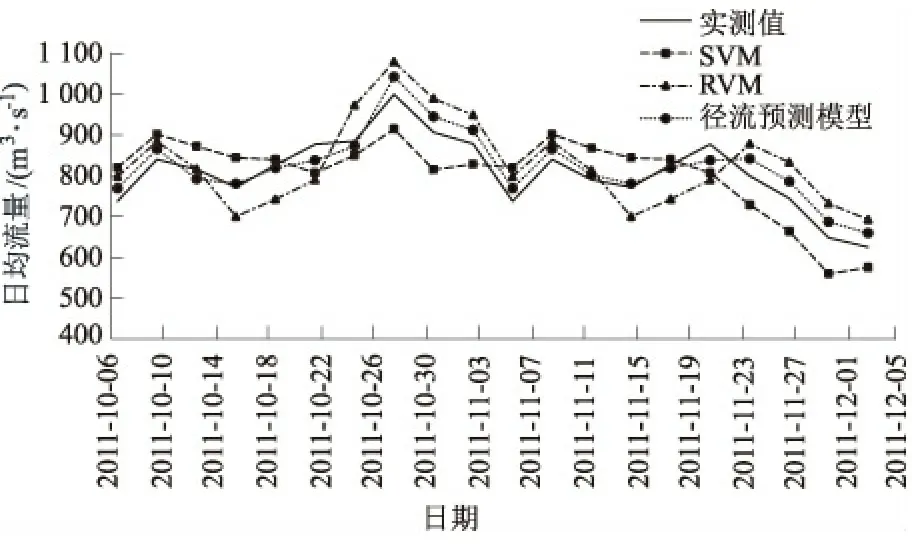
图3模型预测效果
Fig.3Predictionresultsofthreemodels
4 结 论
通过分析研究,本文取得的主要结论有:
(1)针对传统径流预测模型对非平稳、非线性、随机性时间序列预测效果并不理想,采用小波分解及重构方法将非平稳的径流时间序列平稳化,有效提高了预测精度。
(2)结合小波分解及重构方法,建立以RVM为理论基础的径流预测模型,采用改进粒子群算法进行核参数寻优,并利用Arima模型对预测结果进行误差修正,通过实例证明,该模型在径流预测中效果较好。
(3)通过实例计算,将径流预测模型与标准SVM模型、RVM模型进行对比,3种模型的预测值平均误差分别为8.60%,9.02%,3.64%,证明基于小波分解及Arima误差修正的径流预测模型具有更高的预测精度,在实际工程中具有一定可行性。
结合小波分解法及Arima误差修正的径流预测模型大大提高了预测精度,在分析预测过程中发现,利用小波分解法得到的子序列质量对最终预测结果的影响较大,对小波分解及重构算法的改进可作为今后研究方向之一。
