基于聚类和自适应神经模糊推理系统的数控机床绿色度评价方法
2018-12-19王宇钢修世超
王宇钢 修世超
1.辽宁工业大学机械工程与自动化学院,锦州,1210002.东北大学机械工程与自动化学院,沈阳,110819
0 引言
近年来,随着制造业的快速发展,我国数控机床产量和保有量逐年增长。在生产过程中,数控机床不仅会消耗大量电能和资源,还会产生大量废物污染环境。对数控机床进行绿色度评价,获得其对环境友好性的综合评分,以实现对环境影响的最小化,符合绿色制造的要求,具有现实意义[1-2]。
目前,国内外学者对机床的绿色度评价已开展了大量的研究工作,探寻建立有效的评价方法。陈薇薇等[3]通过分析切削参数对数控机床能耗的影响,将切削速度、切削深度和进给量作为输入,将切削功率作为输出,提出一种基于支持向量机算法的数控机床能耗预测模型,并经实验验证了该方法的有效性和可行性。王贤琳等[4]利用可拓层次分析法为指标权重赋值,将能值分析理论与模糊评价法相结合,建立数控机床绿色度综合评价模型。潘尚峰等[5]针对机床基础部件再制造问题,提出基于改进BP神经网络的评价模型。曹华军等[6]将生命周期评价方法应用于机床的碳排放评估,通过建立的线性特性方程分析和计算机床生命周期各阶段碳排放量,并将碳排放效率用于评估机床碳排放随时间的变动特性。
人工智能由于可以模拟人的意识和思维去完成模糊和复杂问题的分析处理过程,已被广泛应用于决策专家系统。人工智能算法对“经验”的依赖性很强,需要不断从已有的经验中获取知识、学习策略,当再遇到类似的问题时,运用已有经验去解决问题并积累新的经验[7]。应用人工智能算法对产品绿色度进行评价,可以有效避免对同一对象由于专家主观判断而对评价结果产生的较大影响,同时由于可以应用已有经验去进行分析决策,而不必如生命周期法在经过评价对象整个生命周期结束后才能给出评价结果,故可做到事前评价,节省大量时间和成本。人工智能算法在实际应用时,需注意学习的“经验”,即训练样本集通常由人为凭经验划定,这使得评价结果易受人的主观影响。
本文针对数控机床绿色度评价问题,提出一种基于聚类和自适应神经模糊推理系统(adaptive neuro-fuzzy inference system,ANFIS)的评价方法。建立的评价模型为多输入单输出推理系统,利用粒子群优化模糊C均值(FCM)聚类算法自适应划分样本空间,提供合理的训练样本集,ANFIS通过对样本集的学习,自适应地建立从输入到输出的模糊映射规则,从而实现对评价样本的有效预测。
1 评价指标体系的建立
数控机床绿色度评价是涉及加工质量、环境影响、能源利用、资源消耗和生产成本的多目标优化决策问题。在满足工艺要求条件下,绿色数控机床的评价需根据绿色制造要求,选择通用性好、有代表性的指标。为量化评价指标,将评价指标分为定性指标和定量指标。对于定性指标,由专家采用十分制打分方法进行量化,对于定量指标直接采用测量值。以某数控机床为例,考虑各种工艺过程对环境影响显著指标[8],建立表1所示绿色度评价指标体系。指标描述时,按极小型指标赋值(值越小绿色度越好)以作为评价模型的输入项。
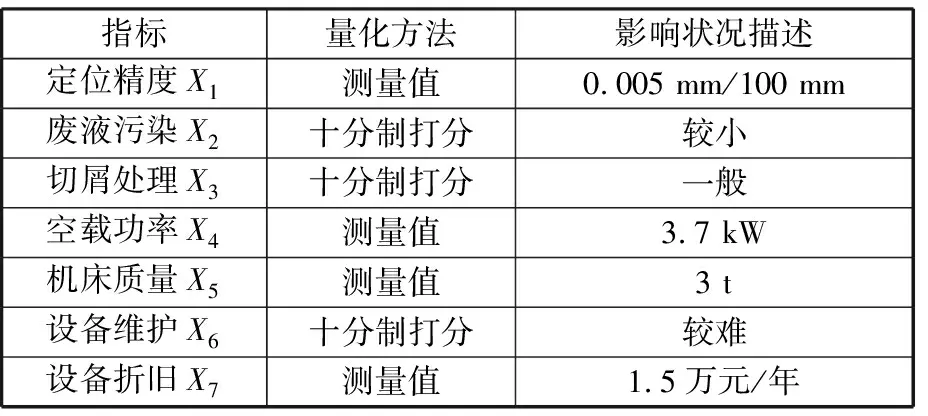
表1 某数控机床绿色度评价指标体系
2 评价模型原理
由于评价问题的复杂性及评价指标的不确定性,对数控机床绿色度进行准确地评价是非常困难的。为获得准确、客观的评价结果,评价方法应满足以下要求:合理地处理定量指标和定性指标;能够体现不同层次、不同评价对象之间的关系;给出直观的评价结果。自适应神经模糊推理系统既具有易于表达人类知识的模糊逻辑,又具备神经网络自学习能力,且具备对非线性映射任意逼近的特点,因此特别适用于推理规则还不被完全了解或结构非常复杂的评价系统[9]。
2.1 粒子群优化FCM聚类算法
FCM聚类算法是目前应用最广泛的一种模糊聚类算法。设有L个类簇的数据样本集合X={x1,x2,…,xn}∈Rp,n为样本个数,p为样本空间维数,L介于2~n之间。目标函数定义为
(1)
(2)
(3)
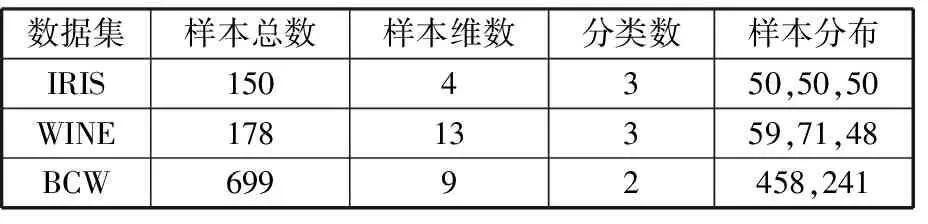
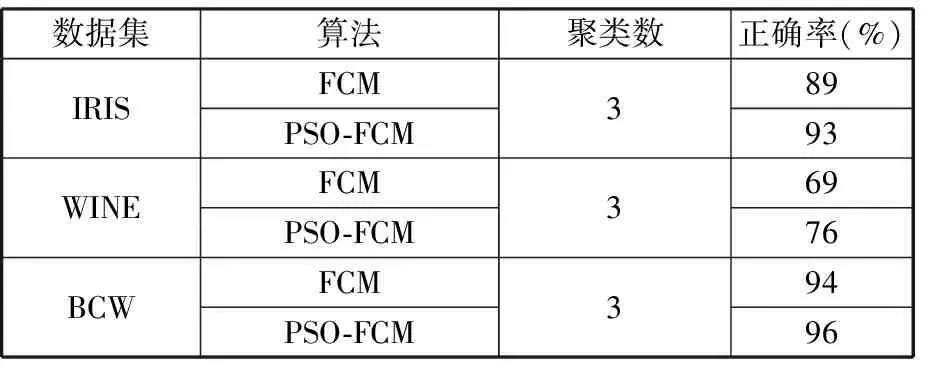
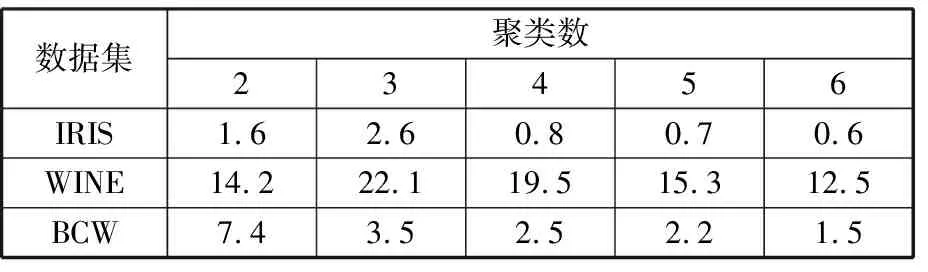
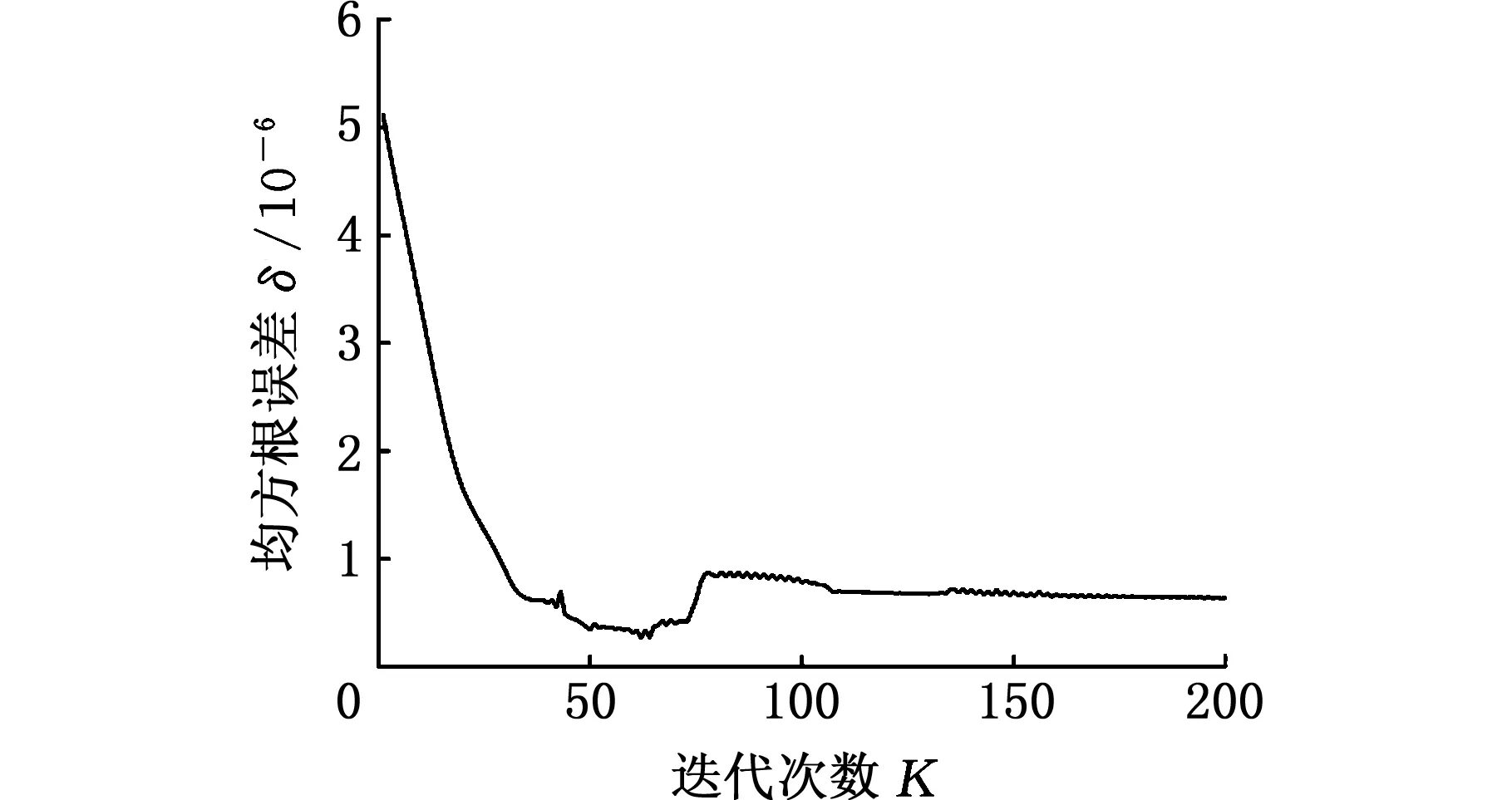
式中,J(U,V)为目标函数值;U为隶属度矩阵;V为聚类中心;dij为样本与聚类中心间距即欧氏距离,dij=‖xj-Vi‖;m为模糊加权指数;uij为数据集X中的第j个样本对第i类的隶属程度(0 由于FCM聚类存在对初始聚类中心敏感,易于陷入局部最优解的缺陷,文献[10]通过粒子群优化(PSO)算法与FCM算法融合来改善聚类性能。在粒子群优化FCM(PSO-FCM)算法中,每个粒子代表一个个体,种群就是由这些粒子构成,以粒子自身当前最优位置pi和群体全局最优位置g影响粒子的运动速度和位移,所求问题的解就是粒子的最优位置。 为提高聚类效果,对PSO-FCM算法进行改进。采用带邻域的粒子群优化PSO-FCM聚类算法,即将聚类中心作为种群中粒子的位置,将FCM算法目标函数作为适应函数,引入环形拓扑结构邻域pl,将邻域也作为粒子进化的一个调节源,降低早熟收敛情况发生概率,终止条件为相邻目标函数适应值之差小于阈值或迭代次数达到设定值[11-12]。 采用的粒子速度vi和位移si更新形式为 vi+1=wvi+c1r1(pi-si)+c2r2(g-si)+c3r3(pl-si) (4) si+1=si+vi+1 (5) 式中,c1、c2、c3为学习因子;r1、r2、r3是[0,1]之间的随机数;w为惯性权重,在[wmin,wmax]之间取值;pl为粒子邻域极值。 将粒子的初始位置均布于取值范围[Xmin,Xmax],Xmin、Xmax分别为样本每维最小值和最大值组成的向量。这样初始化的粒子可在接近最优解的搜索空间开始进化运算,提高聚类质量,缩短收敛时间。 粒子在样本空间每一维都会定义一个最大速度vmax,限定粒子移动速度范围[-vmax,vmax]。使粒子在一次循环中每一维的移动最大距离得到优化。最大速度定为 vmax=λ(Xmax-Xmin) (6) 式中,λ为常数。 聚类有效性指数可用于判定最优聚类个数。文献[13]提出一种使用隶属度矩阵定义的聚类有效性指数Vcs,由紧致度C和离散度S比值构成,评价准则为Vcs指数的值越大,聚类结果越好,表达式如下: (7) Sij=min(uik,ujk) k=1,2,…,n 式中,Cij为第i类和第j类样本间的紧致度;Sij为第i类和第j类之间的离散度。 本文提出的PSO-FCM聚类算法流程见图1。 图1 算法流程图Fig.1 Flow chart of algorithm ANFIS将神经网络与模糊控制有机结合, 通过引入人类经验和知识(规则)构建输入输出的非线性映射模型,并且通过不断地反复学习训练数据更新自己的系统参数,产生一个自适应的模糊推理系统。设有M个输入变量x1,x2,…,xM, 一个输出变量y的系统, 同一层每个节点具有相似功能,其参数学习采用反向传播算法与最小二乘法的混合算法。基于一阶Sugeno模型的ANFIS结构见图2。 图2 ANFIS结构图Fig.2 Structure chart of ANFIS (8) 式中,μA(x)为模糊集A的隶属函数,一般选择钟形函数。 第2层:将输入进行相乘运算,输出每条规则激励强度ω,即 (9) 第3层:将各条规则的激励强度归一化,即 (10) 第4层:该层每个节点i为自适应节点,输出为 (11) 第5层:该层为单节点,计算系统总输出,即 (12) 选择来自机器学习数据库UCI的3个真实数据集IRIS、WINE和BCW(breast cancer wisconsin)验证本文聚类算法的性能。3个数据集信息见表2。 表2 数据集信息 对3个数据集分别采用FCM算法和本文的PSO-FCM算法(粒子种群数为20,c1=c2=c3=2,最大迭代次数100, 最优解改变量阈值0.01,允许的最大速度系数λ=0.15)进行聚类实验,经10次仿真计算取平均值,结果表明PSO-FCM算法比FCM算法具有更高的分类正确率,如表3所示。 表3 聚类结果 3个数据集在不同聚类个数下,采用PSO-FCM算法计算相应的聚类有效性指数值Vcs,根据获得的最大Vcs值确定最佳聚类数。仿真结果表明Vcs可有效确定最佳聚类数,如表4所示。 表4 数据集不同聚类数的Vcs 选取较典型的数控机床为样本对象,对采集数据按照定性指标和定量指标量化,以各指标数据最大值作为基数(定量指标为测量值,定性指标为10),将各指标值与其最大值相除进行归一化处理。归一化后的样本数据见表5。 采用PSO-FCM算法聚类,由Vcs最大值确定最佳聚类数为3,不同聚类数下的Vcs值见表6。 Vcs取最大值时,得到的样本数据聚类中心 在实际应用中,为满足用户或专家的需要可为样本指标赋予权重。采用专家咨询方式,按十分制赋值,根据10位专家打分取平均值获得主观权重向量B: 表5 评价样本量化数据 表6 样本集不同聚类数的Vcs 将聚类中心和主观权重向量的转置相乘,得到各个类别的判别值: (13) 判别值越小表明绿色度越好,所以根据聚类结果设定期望值:评价结果为“优”时,系统输出期望值设置为0.2;评价结果为“良”时,系统输出期望值设置为0.5;评价结果为“差”时,系统输出期望值设置为0.8。最终生成的评价样本结果见表7。 表7 样本聚类结果 为测试评价系统的有效性,训练样本与测试样本均应含有三类期望值。将表5中序号1~17的样本作为训练样本,用于ANFIS“学习”,序号18~22的样本作为测试样本,检验系统评价有效性。 评价模型训练的均方根误差迭代曲线见图3。由图3可知,均方根误差随迭代次数逐渐收敛,当迭代数超过150次时,均方根误差趋于稳定,表明模型经训练有效。 图3 均方根误差迭代曲线Fig.3 Iterative curve of root mean square error 将5个测试样本依次输入评价系统模型,经计算得到测试样本评价输出值和绝对误差,如表8所示。 表8 测试样本计算结果 由表8可知,测试样本的绝对误差值均小于0.1,表明设计的评价模型在学习之后具有较好的预测精度,反映出评价系统的良好有效性。 针对数控机床绿色度评价问题,提出一种基于聚类和ANFIS的评价模型。在模糊推理系统的设计中,由于设计者经验的局限性,依靠用户已有经验而建立的模糊规则无法保证最优的推理性能,因此,采用粒子群优化FCM聚类算法对量化的数据样本进行聚类分析,自适应地划分样本空间,生成合理的训练样本集。ANFIS通过对已知数据的学习自动生成模糊控制规则,即可以实现自适应推理。经实例验证该方法可实现对数控机床绿色度的智能评价。该方法为产品的绿色度预测提供一种新的方案。
2.2 自适应神经模糊推理系统
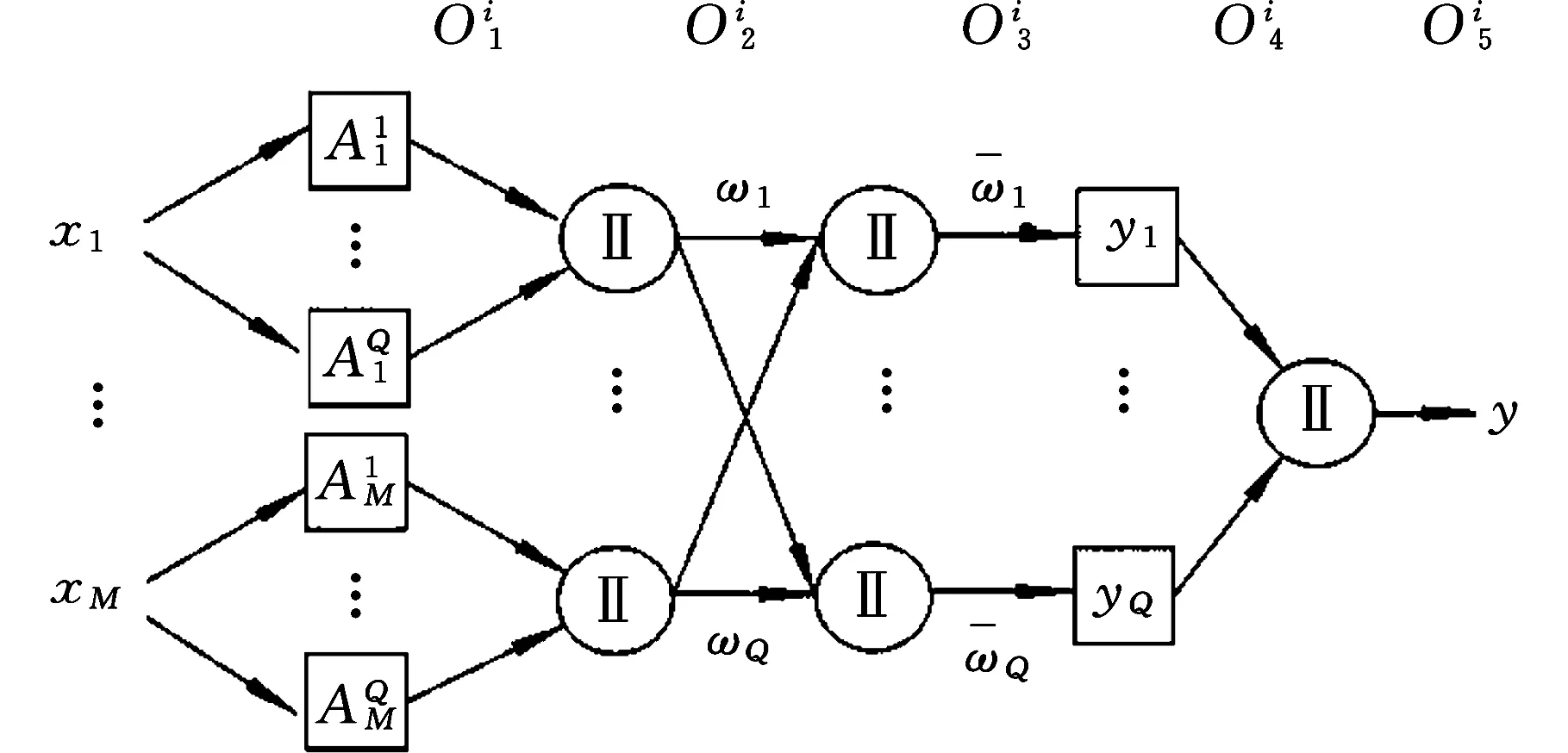
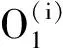
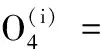
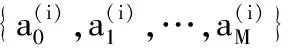
3 聚类算法仿真实验
4 系统的应用
4.1 样本集的构造

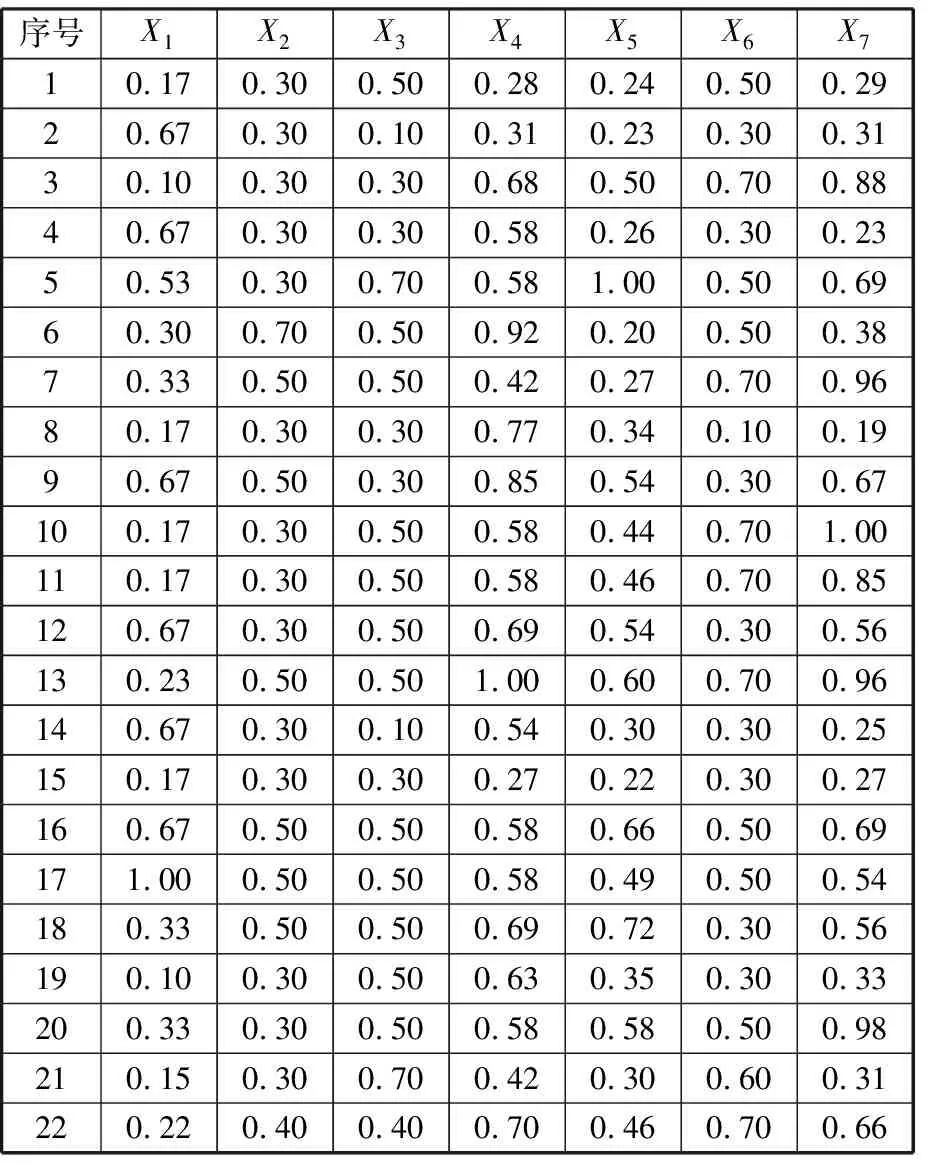

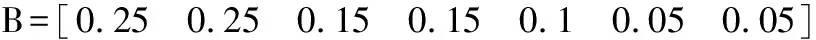

4.2 系统测试

5 结论
