不相关并行机节能调度问题建模

孟磊磊 张超勇 詹欣隆 洪 辉 罗 敏

1.华中科技大学数字制造装备与技术国家重点实验室，武汉，4300742.湖北汽车工业学院电气与信息工程学院，十堰，442002

0 引言

据统计，我国拥有机床800多万台，每台机床平均功率按10 kW算，总功率超过8 000万kW，耗电量是总装容量为2 250万kW的三峡电站的3倍多[1]。然而，机床在实际生产中，大部分时间处于空载状态，据统计，机床大约80%的能量消耗在待机以及关机重启过程中，真正用于加工的能量占比不足20%[2]，GUTOWSKI等[3]给出的一条汽车自动生产线的能量效率只有14.8%。机床处于空闲等待状态所消耗的能量为无效能耗，节能调度的主要目的就是减少这部分能耗。

并行机调度问题(parallel machine scheduling problem，PMSP)在实际生产制造过程中比较常见。不相关并行机调度问题(unrelated parallel machine scheduling problem, UPMSP) 是PMSP中最普遍的一类问题, 工件的加工时间取决于所分配的机床，UPMSP已经被证明为NP-hard问题。目前，对UPMSP的研究主要集中在最小化最大完工时间、成本、交货率等方面[4-6]，而对车间能耗方面不太重视。

当机床连续待机时间较长时，对于允许中途关机的机床可以通过关机/重启策略来减小机床待机能耗。关机/重启策略最早由MOUZON等[2]提出，通过对非瓶颈机床实行关机/重启策略，避免机床长时间处于空闲状态，可以节约80%的待机能耗。随后关机/重启策略逐步被应用于单机[7]、并行机[8-11]调度研究。

针对UPMSP，文献[12]以加权拖期成本和能耗成本之和为目标，提出了求解该问题的多种启发式规则方法。文献[13]研究了并行机批量调度问题，以最小化能耗和最大完工时间为目标，提出了一种基于Pareto的多目标蚁群优化算法。针对加工时间可控的UPMSP，文献[14]以最小化能耗和最大完工时间为目标，提出了求解该问题的多目标协同果蝇优化算法；文献[15]同时以最小化加工能耗和最大完工时间为目标，提出了一种高效的多目标memetic差分进化算法。

UPMSP可以通过精确方法，如混合整数规划(mixed integer programming ,MIP)模型、分支定界等[16]方法求解，也可通过元启发式方法(如遗传算法[17]、蚁群算法[8]、分布估计算法[5]等)和启发式规则[12]等方法求解。精确算法求解速度慢，对于中大规模问题甚至很难求出问题的可行解，但是针对小规模问题，精确算法可以求出调度问题的最优方案，而启发式方法和元启发式方法为近似求解方法，虽然在较短时间内可以得出问题的可行解，但解的质量不能保证为最优解。MIP模型是认识调度问题的基础，是探索与挖掘调度分配规则的关键所在[18]。高效的MIP模型可以在相同的时间内得到更好的计算结果，因此构建高效MIP模型具有重要意义。

本文结合UPMSP自身的特点，以节能为目标，考虑关机/重启策略，提出5个解决该问题的MIP模型，并从建模过程、线性化过程、模型尺寸复杂度以及计算复杂度等方面对5个MIP模型进行对比分析。

1 问题描述

1.1 参数定义

参数定义见表1。其中，为保证每台机床上都安排工件加工，每台机床最多可安排n-m+1个工件，每台机床最大位置数为n-m+1。

1.2 UPMSP描述

UPMSP可描述为:n个工件在m台机床上加工，每个工件只有一道工序，且同一工件在不同机床上的加工时间是不同的。该问题满足以下基本假设: 不同工件的释放时间、交货期是不同的；所有工件必须在规定的交货期内完成加工；机床在0时刻处于可用状态；所有工件在所有机床上的加工时间、加工功率等是已知的；同一机床上不同工件间的转换时间忽略不计；任一工件可在任一机床上加工；工件一旦开始加工则不可中断；对于每个机床，在同一时刻最多只能加工一个工件；对于每个工件，在同一时刻最多只能在一台机床上加工。

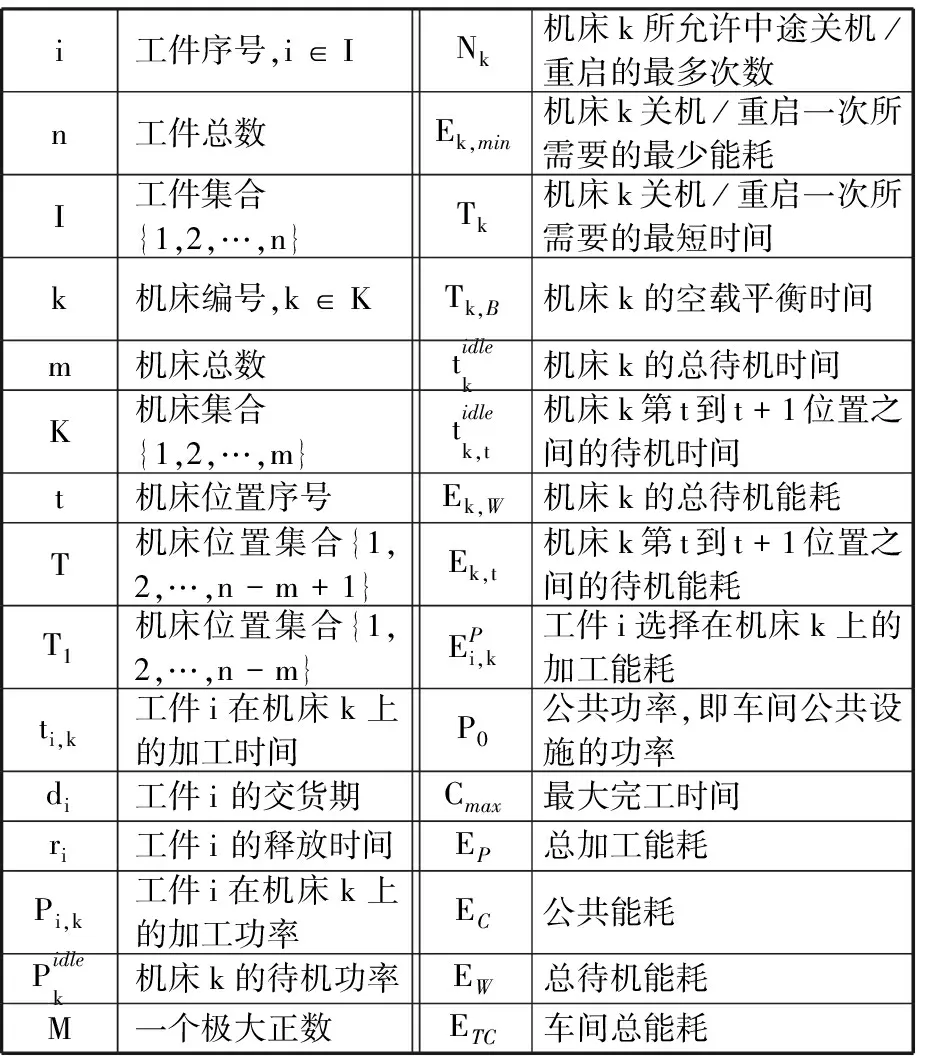
表1 参数定义

UPMSP的目的就是合理地将工件安排在机床上,且确定工件在机床上的加工顺序以达到某些调度目标，如最大完工时间、成本、能耗等的最优。本文研究UPMSP节能调度问题，目标为最小化车间总能耗。

1.3 车间能耗分析与建模

车间能耗主要包括机床能耗、公共能耗两部分，机床能耗进一步可分为加工能耗及待机能耗。

1.3.1加工能耗

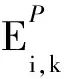
(1)

总加工能耗

(2)

因为每个工件只能选择在一台机床上加工，故引入0-1变量Yi,k，如果工件i选择在机床k上加工，则Yi,k=1，否则，Yi,k=0。

1.3.2待机能耗

待机能耗是指由于上一工件已经加工完，下一个工件还没有到达，从而使机床出现闲置状态所消耗的能量，机床k的第t到t+1位置之间的待机能耗

(3)

式中，Fk,t为机床k上第t个位置的结束时间；Sk,t为机床k上第t个位置的开始时间。

机床k的总待机能耗

(4)

所有机床总待机能耗

(5)

1.3.3公共能耗

公共能耗是指车间公共设施的能源消耗，是指为了维持车间正常运行所必须消耗的能源，主要包括照明、通风、供暖、空调等耗能，其值为公共功率P0与最大完工时间Cmax的乘积，可表示为

EC=P0Cmax

(6)

1.3.4车间总能耗

车间总能耗ETC为总加工能耗、待机能耗以及公共能耗之和:

(7)

当机床的一个连续待机时间段Sk,t+1-Fk,t比较长时，可以实施关机/重启策略，节约无用待机能耗，实现关机/重启策略的最短待机时间，即空载平衡时间

(8)

空载平衡时间Tk，B表示机床在空载的过程中，当空载的时间不小于一次关机/重启策略所需要的时间Tk，且机床空载所消耗的能耗不小于机床一次关机/重启所需要的能耗Ek,min时才可实施关机/重启策略。

当引入关机/重启策略后，待机段能耗Ek,t可表示为

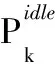
(9)

当引入关机/重启策略后，车间总能耗

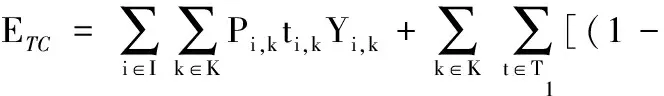
(10)

其中，Zk,t为0-1变量，用来控制是否实行关机/重启策略，当Zk,t=1时，表示在机床k的第t到t+1位置之间实行关机/重启策略，此时Ek,t为一次关机/重启所需要的能耗Ek,min；否则,Zk,t=0，Ek,t根据具体待机时间而定。

2 混合整数规划模型构建

目前关于UPMSP的MIP模型较多, 但是大部分是针对时间目标的[16-17,19]。本文针对UPMSP自身的特点，以节能为目标，同时考虑关机/重启策略，基于机床位置的Wagner建模思想[20]，建立5个考虑关机/重启策略的MIP模型，其中2个为基于空闲时间的非线性模型，3个为线性模型(2个线性模型通过将2个非线性模型引入中间决策变量进行线性化处理得到，第3个线性模型基于空闲能耗的建模思想直接构建)。

基于机床位置的Wagner建模方法建立在“机床位置”概念上，即将一个机床按照时间先后分成若干个段，每一段即成为一个位置，一个位置最多只能安排一个工件，因此，只要确定了工件与机床位置的对应关系，工件在机床上的排序即可得到。

5个MIP模型按照建模思路可进一步细分为两类：第一类是基于空闲时间的建模方法，包括非线性模型1、线性模型1与非线性模型2、线性模型2；第二类是基于空闲能耗的建模方法，包括线性模型3。基于空闲时间的建模方法是指机床待机能耗通过待机段时间与待机功率来计算，而基于空闲能耗的建模方法直接定义空闲段能耗决策变量。

因为基于Wagner建模方法的MIP模型必须引入机床位置占用变量Xi,k,t，Xi,k,t与机床选择变量Yi,k存在对应关系，因此本文5个模型将不再使用Yi,k，以减少0-1决策变量数，降低模型复杂度。对应关系如下：

(11)

2.1 模型1

模型1包括非线性模型1以及线性模型1。其中线性模型1通过引入中间决策变量将非线性模型1的目标函数进行线性化处理之后得到。

非线性模型1有Xi,k,t、Zk,t、Sk,t及Cmax4个决策变量，其中，Xi,k,t用于确定工件的机床位置选择，Zk,t用于确定在机床相应位置是否实行关机/重启操作，Sk,t和Cmax为连续决策变量。Xi,k,t和Zk,t的表达式分别如下：

为了将非线性目标函数进行线性化处理，引入中间决策变量Ai,k,t、Uk,t和Wk,t，其中Uk,t、Wk,t为连续决策变量，Ai,k,t为0-1中间决策变量，因此线性模型1共有Xi,k,t、Zk,t、Sk,t、Cmax、Ai,k,t、Uk,t和Wk,t7个决策变量。

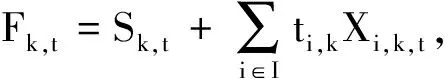
非线性模型1的目标函数为

(12)

式(12)中，等号右边第一项表示机床总空闲能耗(待机或关机/重启)，第二项为机床总加工能耗，第三项为公共能耗。由式(12)可以看出，目标函数是非线性的，存在决策变量相乘的情况，如(1-Zk,t)Sk,t+1、(1-Zk,t)Sk,t以及(1-Zk,t)Xi,k,t，非线性模型求解非常复杂。本文引入中间决策变量Uk,t、Wk,t、Ai,k,t,用Uk,t+1代替(1-Zk,t)Sk,t+1、Wk,t代替(1-Zk,t)Sk,t、Ai,k,t代替(1-Zk,t)Xi,k,t，通过添加相应的约束，实现非线性模型到线性模型的转换。

线性模型1的目标函数为

(13)

约束条件为

(14)

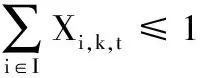
(15)

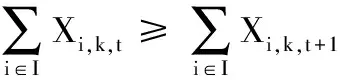
(16)

ri≤Sk,t+M(1-Xi,k,t) ∀t∈T

(17)

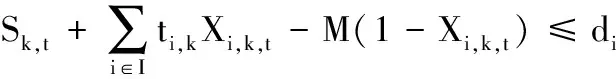
(18)

Sk,t≥0 ∀t∈T

(19)

(20)

(21)

(22)

(23)

Uk,t+1≥Sk,t+1-MZk,t∀t∈T1

(24)

Uk,t+1≤Sk,t+1+MZk,t∀t∈T1

(25)

Uk,t+1≤M(1-Zk,t) ∀t∈T1

(26)

Uk,t≥0 ∀t∈T

(27)

Wk,t≥Sk,t-MZk,t∀t∈T1

(28)

Wk,t≤Sk,t+MZk,t∀t∈T1

(29)

Wk,t≤M(1-Zk,t) ∀t∈T1

(30)

Wk,t≥0 ∀t∈T1

(31)

Ai,k,t≤Xi,k,t∀t∈T1

(32)

Ai,k,t≤1-Zk,t∀t∈T1

(33)

Ai,k,t≥Xi,k,t-Zk,t∀t∈T1

(34)

式(14)～式(34)中，∀i∈I，∀k∈K。式(14)表示任一工件只能选择在一个机床上加工，且只占用该机床的一个位置；式(15)表示任一机床的任一位置最多只能安排一个工件加工；式(16)表示任一机床的位置按照先后顺序安排工件加工；式(17)表示工件只能在到达之后才可以开始加工；式(18)表示工件必须在交货期内完成加工；式(19)约束决策变量范围；式(20)表示最大完工时间约束；式(21)、式(22)表示关机/重启策略约束，约束当机床k的t到t+1位置间存在关机/重启策略时，即Zk,t=1, 第t+1位置的开始时间与第t位置的开始时间加上该位置的加工时间之差必不小于机床k的空载平衡时间Tk,B,否则，不存在关机/重启策略；由于平时加工过程中，机床是不允许频繁关机重启的(频繁关机重启对机床电器元器件寿命影响很大)，因此引入式(23)来限制关机重启次数; 式(24)～式(27)约束Uk,t+1=(1-Zk,t)Sk,t+1恒成立，其中，成对约束(式(24)与式(25))保证了当机床k的t到t+1位置间不存在关机/重启策略时，即Zk,t=0时，保证Uk,t+1=(1-Zk,t)Sk,t+1成立；式(26)、式(27)保证了Zk,t=1时，Uk,t+1=(1-Zk,t)Sk,t+1成立，同理，式(28)～式(31)保证了Wk,t=(1-Zk,t)Sk,t恒成立，式(32)～式(34)保证了Ai,k,t=(1-Zk,t)Xi,k,t恒成立。

2.2 模型2

模型2包括非线性模型2和线性模型2。与模型1相比，模型2引入连续决策变量Fk,t，从而减少目标函数中的非线性项、中间决策变量以及相应约束的数量。

非线性模型2的目标函数中含有非线性项(1-Zk,t)(Sk,t+1-Fk,t)，通过引入中间决策变量线性化后即为线性化模型2的目标函数。线性化过程与模型1相似，引入中间决策变量Uk,t、Vk,t，分别代替非线性项(1-Zk,t)Sk,t+1、(1-Zk,t)Fk,t，实现非线性目标函数到线性目标函数的转换。

模型2中的决策变量为：Xi,k,t、Zk,t、Sk,t、Cmax、Uk,t(含义与模型1中的相同)；机床k上第t个位置的结束时间Fk,t；用来代替非线性项(1-Zk,t)Fk,t的中间决策变量Vk,t。

非线性模型2的目标函数为

(35)

线性模型2的目标函数为

(36)

约束条件为

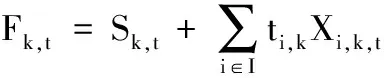
(37)

Fk,t-M(1-Xi,k,t)≤di∀t∈T

(38)

Fk,n-m+1≤Cmax

(39)

Sk,t+1-Fk,t≤Tk,B+MZk,t∀t∈T1

(40)

Sk,t+1-Fk,t≥Tk,BZk,t∀t∈T1

(41)

Vk,t≥Sk,t-MZk,t∀t∈T1

(42)

Vk,t≤Sk,t+MZk,t∀t∈T1

(43)

Vk,t≤M(1-Zk,t) ∀t∈T1

(44)

Vk,t≥0 ∀t∈T1

(45)

其中，∀i∈I，∀k∈K。式(37)表示机床位置结束时间等于其开始时间加上安排在该位置工件的加工时间；式(38)～式(41)的含义分别与式(18)、式(20)～式(22)约束含义相同；式(42)、式(45)用来约束Vk,t=(1-Zk,t)Fk,t恒成立，其中式(42)～式(43)用来约束当Zk,t=0时，Vk,t=Fk,t=(1-Zk,t)Fk,t成立，式(44)、式(45)用来保证当Zk,t=1时，Vk,t=0=(1-Zk,t)Fk,t成立。

2.3 模型3

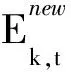
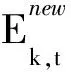
模型3的目标函数为

(46)

约束条件为

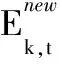
(47)

(48)

∀k∈K,t∈T1

3 模型对比

模型对比从尺寸复杂度与计算复杂度进行，尺寸复杂度主要包括0-1决策变量数、约束数以及连续决策变量数3个方面。计算复杂度通过规定时间内可求最优解总数Q来判定，包括目标函数值的容差Gap=0最优解个数Q0与Gap≠0最优解个数Q1。当Q相同时，对比Q0；当Q与Q0都相同时，对比Q1；Q、Q0与Q1越大，模型越好。当Q、Q0与Q1都相同时，对比求解时间ttotal，ttotal也是一个重要评价指标，越小越好。Gap可定义为|SC-SB|/|SC|，其中SC表示目前为止可以找到的最优解，SB表示可能的最优解，是当前所有解的下限。可见，Gap值越小越好，当Gap=0时，则得到问题的最优解，程序会自动停止。由此，Gap值也常作为评价MIP模型求解效果的一个指标。

本文所有混合整数线性模型都由商业软件IBM ILOG CPLEX12.7.1求解，编程语言采用CPLEX Studio自带OPL语言编写。CPLEX可以求解线性模型以及非线性模型。模型运行最长时间设置为3 600 s，所有实例独立运行3次，最终结果取平均值。所有实例在Dell Vostro 3900台式机上运行，该电脑配置为：Win7系统、i5-4460 3.20GHz四核处理器、8G内存。

如果模型在3 600 s之内自行停止，则可得到最优解且可证明所得到的解为最优解，即Gap=0，如果到截止时间3 600 s，程序强制停止，此时有可能得到Gap≠0最优解，但是Gap≠0，是因为虽然求出了最优解，但是在规定时间内不能证明该解为最优的。本文总共测试10组规模不同的实例。因为目前没有关于UPMSP能耗相关的对比实例，因此本文随机生成10组规模不同的实例。

3.1 模型尺寸复杂度对比

表2 每个约束方程的约束数目

表2给出了上文所列每个约束方程的约束数量，结合每个模型所含约束方程，进而可以得每个模型的约束数(表3)。由各个MIP模型的建模过程可得出每个模型的尺寸复杂度，见表3。模型针对具体实例的尺寸复杂度见表4。其中10*2表示工件数*机床数，其他类推。

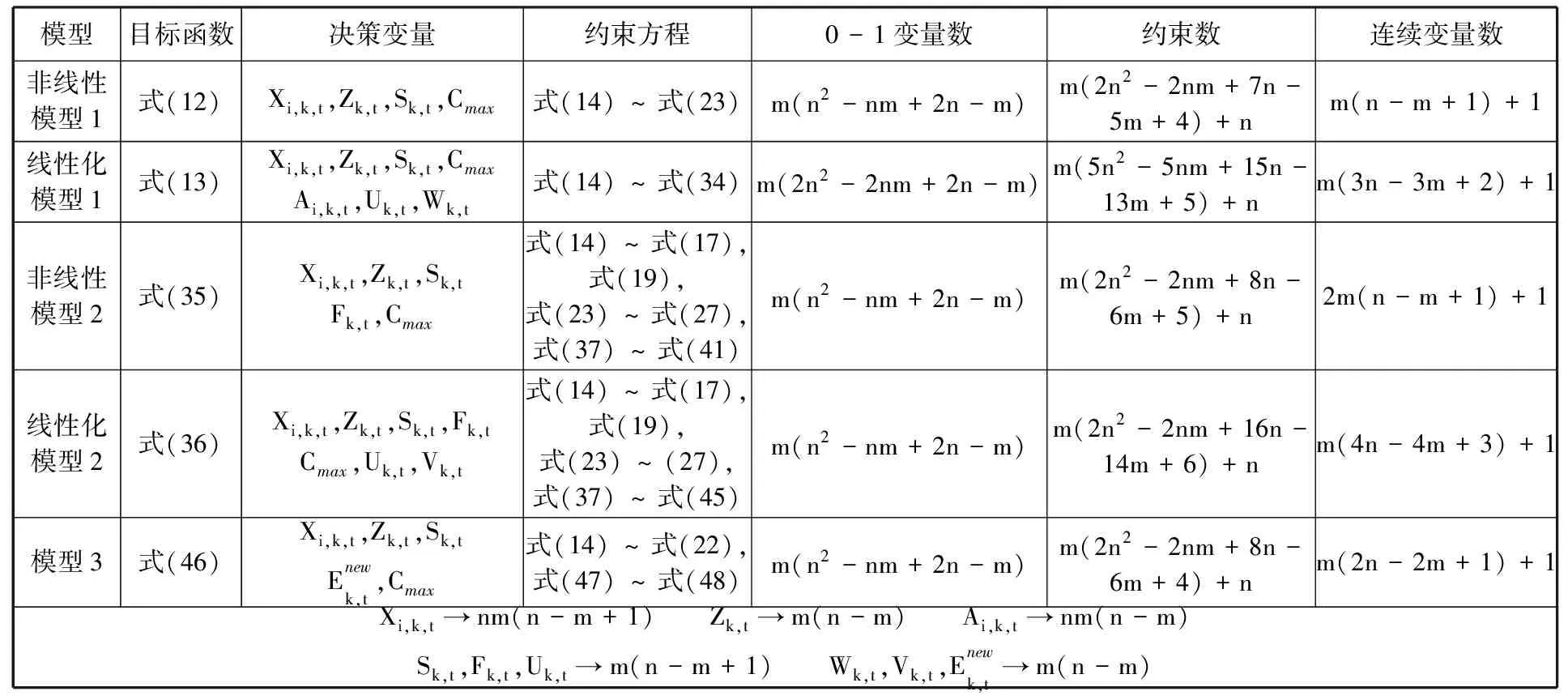
表3 所有模型尺寸复杂度

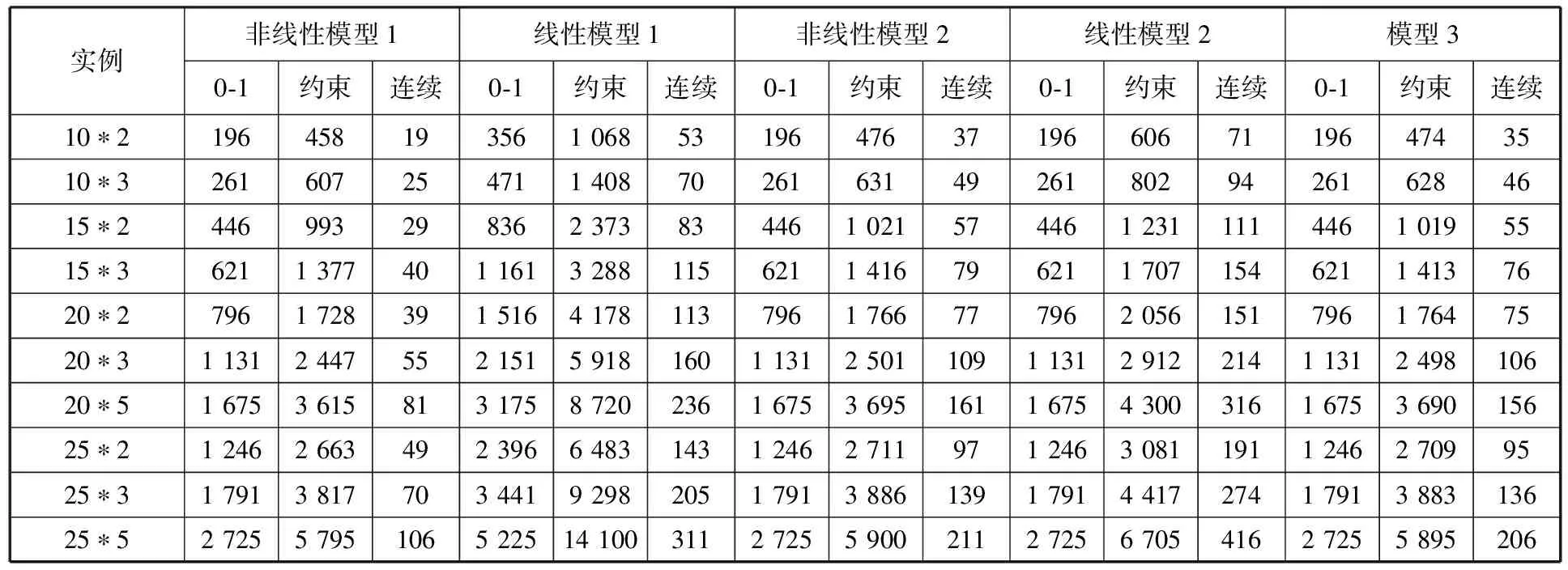
表4 所有模型针对10组实例的尺寸复杂度

通过表3和表4可知，在0-1决策变量数方面，非线性模型1最多，其他模型相同。这是因为其他模型只含有Xi,k,t、Zk,t两个0-1决策变量，而模型1除含有Xi,k,t、Zk,t两个0-1决策变量外，还含有Ai,k,t。

在约束数方面，由表3和表4 可以看出，从多到少依次为线性模型1、线性模型2、非线性模型2、非线性模型1、模型3。这是由于线性模型3基于待机能耗的建模思想，不需要线性化处理目标函数以及相关的约束方程，约束最少。线性模型1需要引入3个中间决策变量(Ai,k,t、Uk,t以及Wk,t)以及相关的约束，而线性模型2只需要引入2个中间决策变量(Uk,t与Vk,t)及相关约束，因此，线性模型1约束数多于线性模型2。非线性模型1与非线性模型2因为没有引入中间决策变量及相关约束，故约束数分别少于线性模型1与线性模型2。

在连续决策变量数方面，由表3和表4可以看出，连续决策变量数从多到少依次为线性模型2、线性模型1、非线性模型2、模型3、非线性模型1。

3.2 模型计算复杂度对比

决策变量数以及约束数严重影响MIP模型的求解效率。对MIP模型影响程度从大到小依次为0-1决策变量数、约束数以及连续决策变量数[21]。除此之外，非线性特征对MIP模型的求解效率影响也很大。

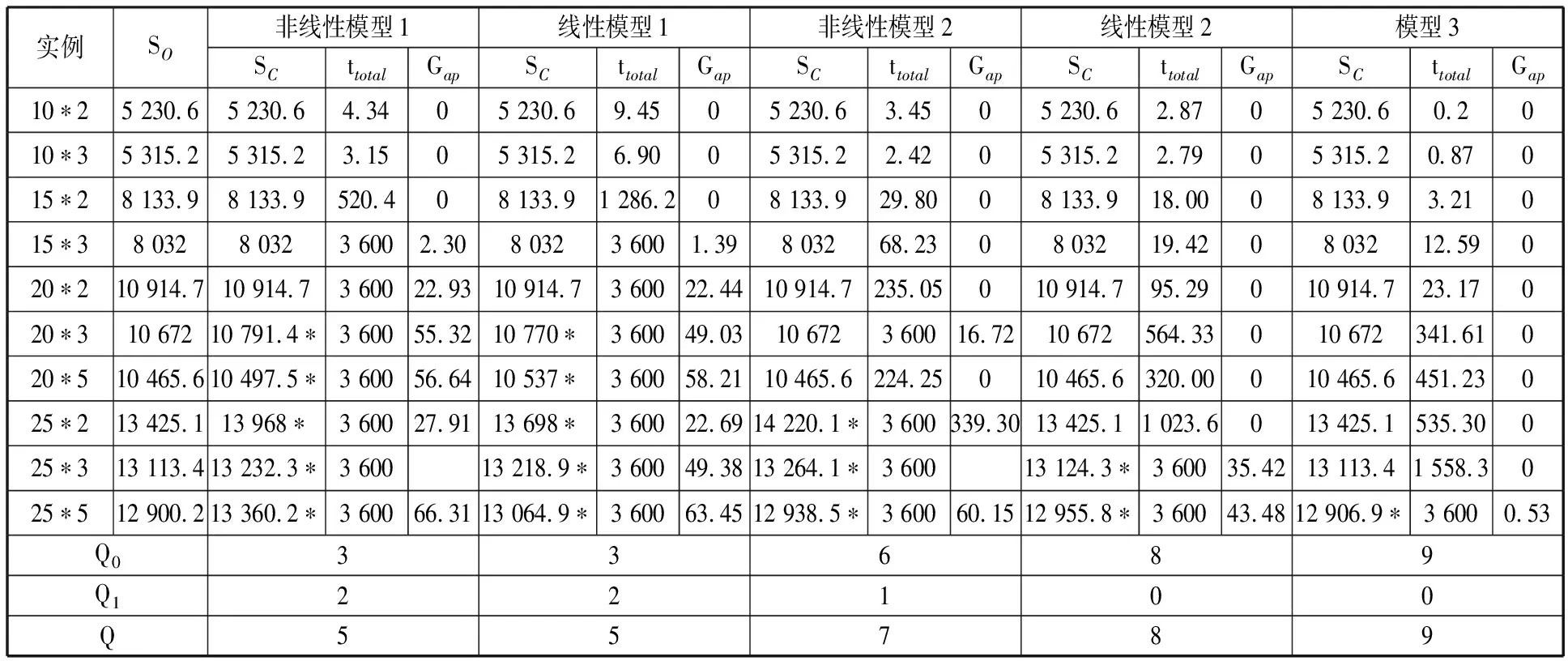
表5 所有模型针对10组实例的求解结果

5种模型针对10组实例的求解结果见表5。其中，SO表示最优解(可通过模型3长时间求解得到)，SC表示当前解(如果在3 600 s内程序自动停止，则为最优解，否则对应3 600 s所能得到的最好解)，带“*”的解表示此解为可行解但非最优解。

由表5可知，在10个实例中，在规定时间3 600 s内，非线性模型1及线性模型1求解效果最差，只可求出10个实例中的5个，包括3个Gap=0最优解以及2个Gap≠0最优解；线性模型1由于引入3个中间决策变量(Ai,k,t、Uk,t、Wk,t)及相关的约束，决策变量数以及约束数远多于非线性模型1，这严重影响了线性模型1的求解效率，因此求解时间长于非线性模型1。

非线性模型2可以求得10个实例中的7个最优解，其中6个Gap=0 最优解以及1个Gap≠0最优解，效果差于线性模型2(其可求得8个Gap=0 最优解)，且求解时间长于线性模型2，这是由非线性模型2的非线性特征影响的。

非线性模型2和线性模型2由于添加了机床位置结束时间决策变量Fk,t，非线性模型2的非线性项少于非线性模型1，线性模型2的0-1决策变量以及约束数远少于线性模型1，因此求解效果好于非线性模型1和线性模型1。

模型3基于空闲能耗的建模思想，目标函数是线性的，不需要对其进行线性化处理以及相应的中间决策变量、约束等，从而使模型3具有最少的0-1决策变量、连续决策变量以及较少的约束数，从而模型3求解效果最好。

除此之外，模型的求解效果还依赖具体实例的加工数据，如针对实例20*5，非线性模型2求解时间为224.25 s，线性模型2求解时间为320.00 s，线性模型3求解时间为451.23 s，非线性模型2的求解效果好于线性模型2以及线性模型3，线性模型2效果好于线性模型3。

3.3 节能策略挖掘

实例25*3的具体数据如表6和表7所示。图1为实例25*3的最优甘特图。对图1进行分析，由于考虑了不同工件释放时间以及交货期，因此每个工件必须在自身释放时间-交货期时间窗内进行加工。工件1～8被分配到机床2上进行加工，机床2在0时刻开机，在212时刻关机。工件10、12、17、18、21、22、25被分配到机床1上进行加工，机床1在230时刻才开机而不是在0时刻开机，从而可以减少待机能耗。工件12在291时刻加工完后，此时下一工件17还没有到达(其释放时间为320)，此时机床将处于长时间待机状态。工件17在363时刻开始加工，在388时刻完成加工，完工时间小于交货期400。时刻291～363长达72的待机时间将导致机床浪费大量待机能耗，在该待机段内对机床1实行关机/重启节能策略，可以节约能耗。机床3同样不是在0时刻开机，而是在199时刻开机以节约能耗，所加工工件依次为9、11、13、14、15、16、19、20、23以及24。由于本文将公共功率设置为20，公共能耗占总能耗比重较大，从而所求能耗最优解中的Cmax也达到了最优(最小)。

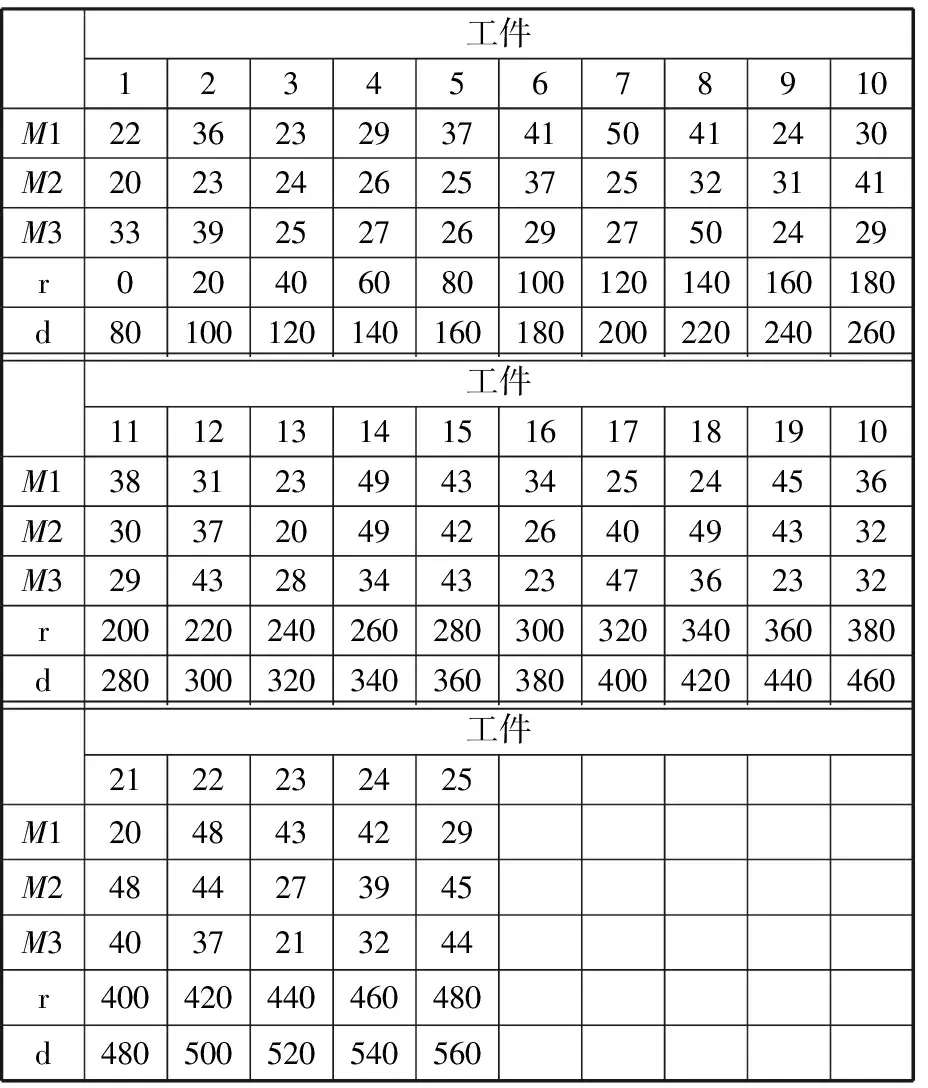
表6 实例25*3加工时间数据

表7 实例25*3加工功率、能耗数据

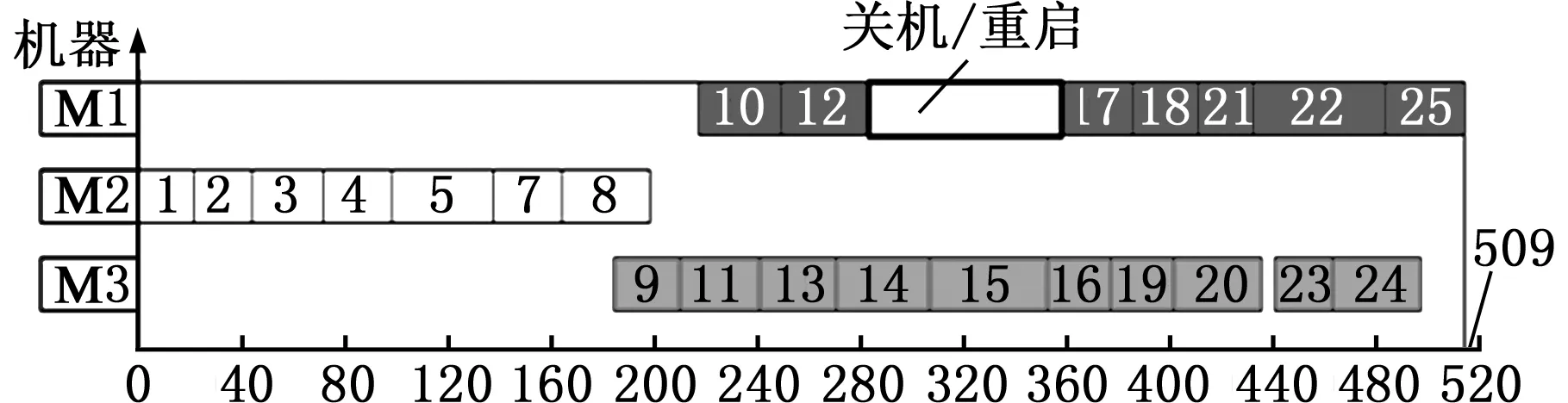
图1 实例25*3甘特图Fig.1 Gantt chart of instance 25*3

可见，在保证最大完工时间不变以及满足交货期的情况下，通过延迟开机以及关机/重启策略可以减少机床待机能耗，达到节能的目的。对节能措施的挖掘有利于以后指导元启发式方法的设计，从而可以有效求解大规模问题。

4 结论

本文以能耗最小为目标，提出了5个考虑关机/重启策略的不相关并行机MIP模型。试验结果表明：基于不同建模思路的MIP模型尺寸复杂度、计算复杂度差别很大，基于空闲能耗的线性化MIP模型求解效果最好，在今后的应用过程中应优先选用。

虽然元启发式方法、启发式规则等在短时间内可以得到问题较好的解，但是即使是对于小规模问题，也不一定能够找到最优解，也无法证明所得到的解是最优的，而通过MIP模型求解则可得到并证明最优解。MIP的求解结果可以作为启发式以及元启发式等近似方法的参照标准。由于本文直接使用CPLEX对问题进行求解，没有加入针对问题特性的求解算法等，因此求解效率较低，下一步研究工作将针对本文问题特性，设计相应的求解规则以嵌入到CPLEX，提高求解效率。