可调螺距螺旋桨单叶静平衡试验台研制

2018-12-19苏世杰付灵懿杨逸琳

中国机械工程 2018年23期

王超苏世杰付灵懿杨逸琳张超

江苏科技大学机械工程学院，镇江，212003

0 引言

可调螺距螺旋桨(简称调距桨)具有与船舶主机良好的匹配性和操纵灵活性，近年来得到了日益广泛的应用[1-2]。为了降低船舶的轴系振动和船体振动，各国船级社均规定调距桨在实船安装前必须进行静平衡试验。

调距桨的单叶静平衡试验是整桨静平衡试验的基础，其目的是将安装在同一桨毂上的每片桨叶的不平衡力矩控制在一定范围内，目前主要有支点平衡、力矩平衡和重心测量3种方法[3-4]。支点平衡法通过人工调节放置在桨叶下方的支点，当桨叶随遇平衡后直接测量不平衡力臂,该方法采用人工操作，进行试验时的随机误差较大，使得试验结果的精度很难保证；力矩平衡法将桨叶安装在专用平衡台上，通过测量平衡配重质量与力臂得到桨叶的不平衡力矩[5]，该方法操作繁琐，同时需针对不同桨叶规格制造对应的毂体，设备成本高；重心测量法通过称重传感器测量放置在桨叶下方3个支点上的支撑反力，并计算出桨叶重心与不平衡力矩[4]，该方法效率高、通用性强，在各领域得到了广泛的应用[6-9]。

梁延德等[10]根据力矩平衡原理和坐标系转换方法建立了调距桨单叶重心倾测系统，该系统具有结构简洁、操作方便的优点，但其原理上增加了垂向测量误差，导致测量精度受到一定的影响。李文强等[11]基于重心测量法，实现了飞机重心的自动测量，但未考虑支点侧向分力及支点间距测量问题。马勇等[12]根据力矩平衡和微幅摆原理，通过在船模下方布置称重传感器实现船模重心位置测量，但该方法对被测物体形状有一定的要求，不适用于桨叶等复杂曲面零件的测量。ZHAO等[13]基于三点测重心原理开发了一重型车辆重心位置测量系统，但该方法未考虑承载平台姿态变化及平台受力变形对测量结果的影响。

为提高调距桨单叶静平衡精度与效率，本文首先分析现有桨叶重心测量方法存在的问题，提出了一种二次称重测量桨叶重心及不平衡力矩的方法，该方法消除了侧向分力及传感器位置测量误差对桨叶重心位置测量精度的影响，有效地提高了桨叶重心测量精度；接着设计了一种双层结构的桨叶静平衡试验台，并基于响应面优化(response surface optimization，RSO)法对上层平台结构进行优化设计；最后研制了一台静平衡试验台样机并进行测量试验，试验验证了该试验台具有较高的重复精度。

1 测量原理和方法

1.1 存在的问题

基于重心测量法的调距桨单叶静平衡试验步骤如下。

(1)将桨叶放置在安装有称重传感器的3个支撑件上，通过角尺保证桨叶底盘法兰端面与水平面垂直，并使桨叶空间姿态水平，如图1所示，则桨叶质量P为

P=P1+P2+P3

(1)

式中，P1、P2、P3分别为3个称重传感器测得的质量。

图1 桨叶的测量调整状态Fig.1 Position adjustment of the blade

(2)建立图2所示的测量坐标系，其中Z轴平行于桨叶底盘法兰面且通过桨轴旋转中心，Y轴为桨叶转动中心线。根据力矩平衡原理，由P1、P2、P3及对应的坐标值(Z1,Y1)、(Z2,Y2)和(Z3,Y3)，可得到桨叶的重心位置(Z,Y)为

(2)

(3)

式中，a为Z轴与桨叶底盘法兰面间的距离。

图2 桨叶测量坐标系Fig.2 Measurement coordinate system of the blade

(3)根据式(1)～式(3)得到桨叶重心位置(Z,Y)与桨叶质量P，则相对于桨轴旋转中心的不平衡力矩MY和相对于桨叶转动中心的不平衡力矩MZ分别为

MY=PY

(4)

MZ=PZ

(5)

该方法原理简单，易于实现测量与计算的自动化，但由于桨叶的特殊形状及较高的测量精度要求，使其在实际应用中存在一些问题而导致测量精度不高：①如图3所示，桨叶为复杂曲面结构，导致桨叶与支撑件之间的接触力与竖直方向存在一定的夹角，故存在由侧向分力所引起的支撑反力测量误差；②需经常调整三个支撑件的位置以适应不同规格的桨叶，而精确测量支撑件的坐标存在一定的困难，故支点坐标测量误差较大；③由于桨叶的曲面结构，导致桨叶与支撑件之间的接触点与支撑件的轴线并不重合，进一步增加了支点坐标测量误差。

图3 侧向分力问题Fig.3 Lateral force problem

1.2 二次称重测重心原理

为了解决上述问题，本文提出了一种图4所示的双层桨叶静平衡试验台结构。可升降的上层平台上布置有1个固定的V形架和2个高度可调的支点，上下层平台之间安装有3个称重传感器和1个升降机。基于该双层结构，提出一种二次称重测量桨叶重心及不平衡力矩的方法，具体步骤如下。

(1)安装桨叶并调整姿态。升降机上升，使上层平台脱离称重传感器；将被试桨叶吊放在V形架及可调支点上，并调整可调支点的位置与高度，以适应不同规格的桨叶并保证桨叶空间姿态水平。

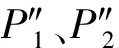
(4)不平衡力矩计算。根据3个称重传感器的坐标(Z1,Y1)、(Z2,Y2)、(Z3,Y3)及步骤(2)、(3)的称重测量值，可分别计算出桨叶质量P、重心位置(Z,Y)、不平衡力矩MY和MZ：

(6)

(7)

(8)

(9)

(10)

图4 双层试验台结构Fig.4 Double-layer structure of tester

该方法的优点如下：①由于称重传感器布置在上下层平台之间，故桨叶与支撑件之间的侧向分力变成了上层平台的内力，消除了因侧向分力所引起的测量误差；②3个称重传感器的位置始终不变，故易于获得其精确坐标，进一步提高了MY、MZ的计算精度；③在安装桨叶时，由于上层平台与称重传感器不接触，避免了可能对传感器产生的机械冲击，提高了传感器的精度稳定性并延长了使用寿命。

2 静平衡试验台总体结构设计

根据上述测量方案，本文设计了图5所示的双层结构静平衡试验台。该试验台由V形夹具体、上层升降机构、上层平台、导向组件、称重传感器、下层升降机构和槽钢架组成。

1.V形夹具体 2.上层升降机构 3.上层平台 4.导向组件 5.槽钢架 6.下层升降机构 7. 称重传感器图5 静平衡试验台的双层结构设计图Fig.5 Design diagram of the static balance tester with double-layer structure

由图5可以看出，V形夹具体和2个上层升降机构安装在可升降的上层平台上，其作用是实现桨叶的安装及空间姿态的调整。V形夹具体可实现桨叶底盘法兰端面的对心(即对桨叶底盘进行定位)；上层升降机构的顶部设计有铜制球头用以保护桨叶叶面，底部安装有电磁吸盘以保证桨叶支撑可靠、避免滑移。导向组件由直线轴承、直线轴承安装套筒、导向轴组成，其作用是保证上层平台在任何工况下均保持一致的空间姿态。导向轴为法兰轴，法兰端面固定在槽钢架上，导向轴外部套有直线轴承；直线轴承安装套筒内部安装有直线轴承，套筒一端为法兰面，固定在上层平台底部。槽钢架为矩形焊接件，用以支撑整个试验台，其上安装有导向组件、下层升降机构和称重传感器立柱。

3 基于响应面优化法的上层平台结构设计与优化

上层平台为试验台的核心承载部件，若其刚度不够，则桨叶安装后会导致上层平台变形，从而对测量精度产生较大的影响；若上层平台过重，则会减少可测的桨叶规格。故需对上层平台的结构进行优化设计，在保证足够刚度的前提下，尽量减少上层平台的整体质量。本文基于响应面优化法对上层平台的结构形式与加强肋的布置进行了优化，有效地提升了上层平台的静力学性能并使其满足轻量化要求，从而保证试验台的测量精度。

3.1 初始结构的静力学分析

图6a和图6b分别为上层平台的初始结构上下表面示意图。考虑到桨叶支撑件在上层平台上的位置分布，设置上层平台的尺寸为1 700 mm×1 500 mm×30 mm，材料为16 Mn，计算得到上平台总质量641.68 kg。

(a)上表面示意图(b)下表面示意图1.V形夹具体 2.上层升降机构1 3.上层升降机构2 4.导向组件 5.称重传感器 6.下层升降机构图6 上层平台的初始结构Fig.6 The initial structure of the upper platform

静平衡试验台共有3种工作状态，分别为不平衡力矩测量状态(C1)、不平衡力矩修正状态(C2)和搬运状态(C3)。设置上层平台在3种工况下的许用应力为180 MPa。为保证测量精度，需要严格限制上层平台在C1状态下的变形量，参考国家标准GB/T 22095-2008，确定该工况下的允许最大变形量为0.025 mm，对其他2种工况则不提出刚度要求。

已知V形夹具体的质量为98.98 kg，每个上层升降机构的质量为35.28 kg。根据最大被测桨叶质量，在接触面1、2、3上的分布质量分别为105.30 kg、132.76 kg和79.44 kg。

图7所示为初始上层平台3种工况下的静应力分析结果。在C1状态下，下层升降机构与上层平台分离，由3个称重传感器进行支撑，经ANSYS分析，由图7a和图7b可以看出，上层平台的最大变形量为0.141 mm，最大应力为17.1 MPa，结果不满足刚度要求；在C2状态下，称重传感器与上层平台分离，由下层升降机构进行支撑，经ANSYS分析，由图7c可以看出，上层平台的最大等效应力为47.6 MPa，结果满足强度要求；在C3状态下，上层平台依靠导向组件中的导向轴支撑，经ANSYS分析，由图7d可以看出，上层平台的最大等效应力为12.6 MPa，其结果满足强度要求。综上可知，上层平台在C1状态下的变形较大，故需改进上层平台的结构，以增强其刚度并减小质量。

(a)C1状态变形量分布图(b)C1状态应力分布图

(c)C2状态应力分布图(d)C3状态应力分布图图7 初始上层平台3种工况下的静应力分析结果Fig.7 The static stress analysis results under three conditions of the initial of the upper platform structure

3.2 初始加强肋的结构布置

根据静平衡试验台的结构特点并结合图7a上层平台的变形量分布图可知，在C1状态下上层平台左右两侧产生的变形较大，因此考虑在上层平台的左右两侧区域布置网状加强肋以增强两侧的刚度；由图7b的应力分布图可知，上层平台在中间区域的应力较大，因此考虑在中间区域布置加强板和加强肋以减小部分应力，从而减少对上层平台整体变形的影响。加强肋结构初始模型的示意图及其变形量分布分别见图8和图9。

图8 加强肋结构初始模型Fig.8 Initial stiffener structure model

图9 加强肋结构初始模型变形量分布Fig.9 Deformation distribution of initial stiffener structure model

由图9可以看出，加强肋结构初始模型的最大变形量为0.017 mm，满足刚度设计要求，但此时上层平台的整体质量大幅增加到972.70 kg，因此需要对上层平台结构采取进一步优化，以减少上层平台的整体质量。

3.3 基于响应面优化法的结构优化设计

利用ANSYS Workbench中的响应面优化(RSO)模块分析输入参数对输出参数的影响，计算得出输入参数间的最优组合，从而实现上层平台的结构优化设计。

根据上层平台结构的设计要求和特点，将需要优化的数据定义为模型输入参数,见表1。设置输入参数(V1～V25)为加强肋的形状和分布位置，输出参数为上层平台的质量与最大变形，其中约束条件Q1为最大变形量(Q1≤0.025 mm)，目标函数Q2为质量最小。

表1 输入输出参数

通过RSO模块中的Design of Experiments项目设置输入参数属性，由于Design of Experiments项目限制一次运算中输入变量不超过20个，因此需要对表1中的25个输入变量进行分批运算。先选取对输出参数影响程度最大的变量作为输入参数，进行上层平台结构的主优化运算，计算筛选出最优设计点并输出过渡模型；再以过渡模型为基础，选取余下的变量进行补充优化运算并输出最终模型。

通过RSO模块中的Response Surface项目，计算得到各输入变量对于输出参数的灵敏度, 如图10所示。

由图10可以看出，在给定变化范围内，V3～V6、V9～V14、V17～V19、V21、V25对最大变形量Q1的影响较大，V1～V14、V25对模型质量Q2的影响较大。由此可知，选取V1～V14、V17～V19、V25作为主优化运算的输入变量，在Design of Experiments项目中共得到550组设计点，通过这些设计点计算每组试验下的上层平台质量和最大变形量。

图10 输入变量对输出参数的灵敏度Fig.10 The sensitivity of the input variable to the output parameter

在主优化运算中，根据上层平台的优化目标，通过RSO模块中的Optimization项目设置筛选条件：最大变形量Q1≤0.025 mm，且模型质量Q2最小，按要求筛选得到最优设计点1。最优设计点1对应的各输入、输出参数见表2。相比于初始上层平台，最优设计点1下的上层平台模型质量减少到540.87 kg，同时最大变形量减小到0.024 mm，实现了对初始上层平台的主优化。

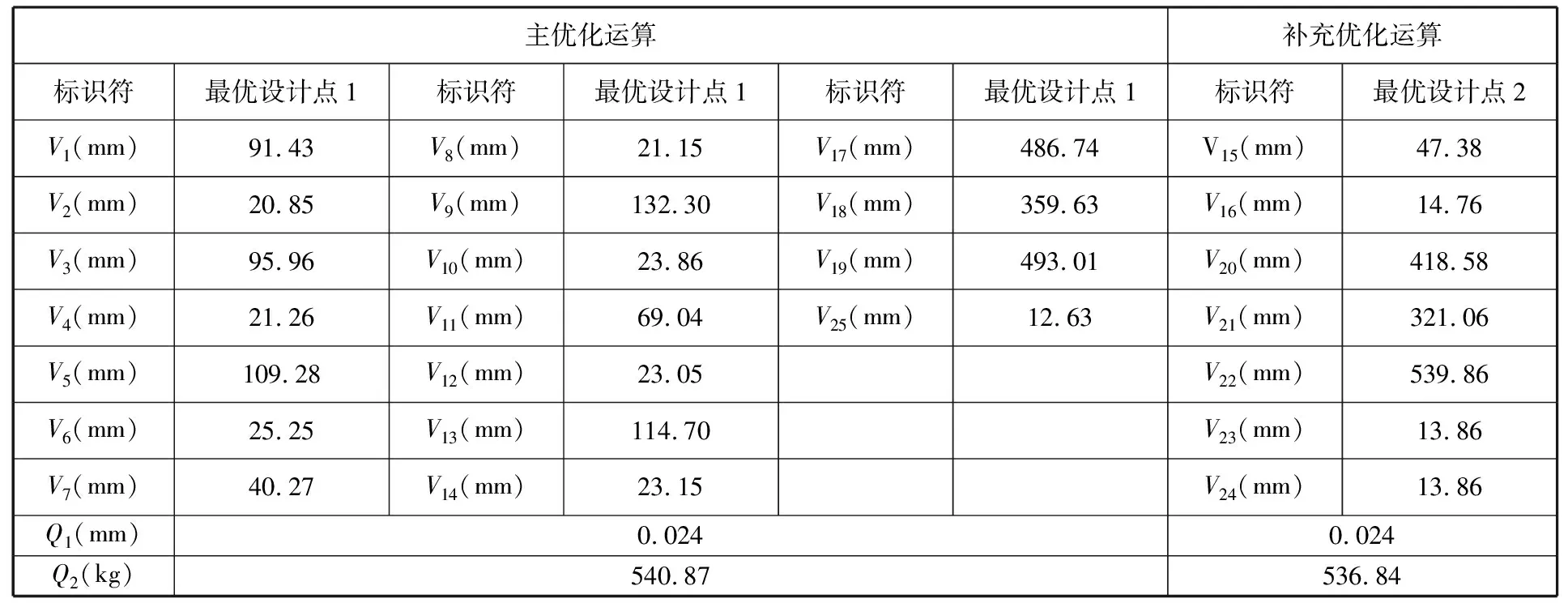
表2 主优化与补充优化运算结果

根据最优设计点1的优化结果设置输入参数，生成上层平台的过渡模型。在过渡模型的基础上，选取剩余7个变量进行补充优化运算，共得到80组设计点。与主优化运算设置相同的筛选条件，得到最优设计点2。最优设计点2对应的各输入、输出参数见表2。相比于上层平台的过渡模型，最优设计点2下的上层平台模型质量减少到536.84 kg，同时最大变形量保持为0.024 mm，实现了对过渡模型的补充优化。根据最优设计点2的优化结果设置输入参数，生成上层平台的最终优化模型。

3.4 响应面优化法的结果分析

图11所示为根据响应面优化法的结果而设计得到的最终上层平台模型,并以此为基础对各个工况进行了静力学分析。优化前后结果对比结果见表3。由表3可知，优化后上层平台的静力学性能有了大幅度的提升，同时通过合理设计加强肋结构、分配加强肋位置，减少了上层平台的整体质量，实现了对上层平台的轻量化设计目标。

图11 最终上层平台模型Fig.11 The final structure model of upper platform

模型类别工况最大变形(mm)最大应力(MPa)质量(kg)满足刚度要求满足强度要求变形变化(%)应力变化(%)质量变化(%)初始上层平台C1状态0.14117.1C2状态47.6C3状态12.6641.68否是是是最终上层平台C1状态0.0244.8C2状态46.3C3状态5.0536.84是是-83.0-71.7是-2.7是-60.5-16.3

4 静平衡试验台的实现与试验分析

根据所提静平衡试验台的工作原理和结构设计，完成了试验台的整体制造与装配与工作，如图12所示，该试验台的设计主参数见表4。图13所示为根据前述优化结果制造的上层平台,采用直径为1.4 m，材质为镍铝青铜合金的调距桨桨叶进行静平衡试验。

图12 静平衡试验台Fig.12 Photo of the static balance test platform

可测桨叶桨高度(mm)600～1 500可测桨叶叶质量(kg)150～350试验台尺寸(长×宽×高)(mm×mm×mm)1 750×1 750×1 670桨叶质量测量精度(kg)±0.1Y向不平衡力矩精度(kg·mm)±80Z向不平衡力矩精度(kg·mm)±50

图13 上层平台Fig.13 Photo of the upper platform

4.1 试验方案与试验数据处理

根据本静平衡试验台的测量原理，一次完整的静平衡试验由空载称重与负载称重组成。试验共进行3组，每组试验完成3次静平衡试验，根据试验测量数据，结合式(6)～式(10)完成质量与不平衡力矩的计算，试验测量数据及其处理结果见表5。

4.2 试验结果分析

根据试验测量结果，桨叶质量测量平均值为323.4 kg，测量的绝对误差限为0.05 kg；Y方向重心位置测量的绝对误差限为0.23 mm，Z方向重心位置测量的绝对误差限为0.28 mm；Y方向静不平衡力矩测量的绝对误差限为124 kg·mm，Z方向静不平衡力矩测量的绝对误差限为72 kg·mm。将桨叶质量和不平衡力矩分别与各自均值作差，绘制出测量误差分析曲线见图14。