基于熵值法径向基神经网络的清扫车吸尘口垃圾颗粒驻留时间预测
2018-12-19赵富强邓海龙解璨铭李玉贵
赵富强 邓海龙 解璨铭 董 竞 李玉贵 王 铁
1.太原科技大学重型机械教育部工程研究中心,太原,0300242.太原理工大学齿轮研究所,太原,030024
0 引言
随着城市化进程的提速升级,道路清扫车逐渐成为解决城市道路保洁的有效工具。吸尘口是清扫车吸尘系统的重要部件之一,其结构设计的合理性直接影响清扫车的吸尘效率。垃圾颗粒驻留时间是研究清扫车吸尘口垃圾颗粒运动规律的要素之一,其时间长短将影响清扫车的吸尘效率。预测垃圾颗粒驻留时间能够为吸尘口结构设计和作业装置转速控制提供可靠依据,因此,有必要建立垃圾颗粒驻留时间预测模型。垃圾颗粒驻留时间受路面颗粒的属性及分布密度、吸尘气流的分布特性、吸尘口结构等多因素的作用,这些因素之间函数关系不明确。垃圾颗粒驻留时间在这些因素的非线性作用下难以用精确的数学模型进行计算。
目前,清扫车吸尘口结构类、固相类和气相类因素对吸尘口垃圾颗粒流动的影响成为该领域的研究方向。文献[1]考虑了出口直径、出口倾角等结构因素对垃圾颗粒运动的气相流场的影响;文献[2]研究了负压气流吸拾垃圾颗粒的仿真分析中扩展区域对气固两相流的影响;文献[3]研究了吸尘口前挡板曲率、后挡板倾角等结构因素对入口气流速度的影响;文献[4]采用了模糊灰色关联模型进行研究,并考虑了吸尘负压、颗粒直径和环境温度3个因素对垃圾颗粒驻留时间的影响;文献[5]考虑了补气流道、腔体等结构因素对垃圾颗粒运动的影响。上述研究均属于考虑单类或两类因素对垃圾颗粒运动特性与驻留时间的研究。
对清扫车吸尘口吸拾性能的求解主要是采用数值模拟和试验方法。其中,文献[6]中提出对吸尘口结构的研究采取数值模拟的方法,但需要以网格划分及网格数量无关性分析为前提,且数值模拟求解耗时长;文献[4]针对干式环卫吸扫车的吸尘口进行了建模和数值模拟,得到了吸尘口内部流场分布、尘粒的运动轨迹及驻留时间,并进行了优化研究;文献[7]通过数值模拟方法分析了吸尘口结构参数对吸尘能力的影响,以优化吸尘口结构。上述研究是采用数值模拟的方法,对吸尘口进行气固两相流仿真,该方法划分网格繁琐、求解困难、仿真速度慢,且对于多因素求解模型,该方法模拟过程复杂,计算过程累计误差大,精度低。吸尘口性能试验研究多采用正交试验的方法,文献[4]采用正交试验设计方法对3个因素影响下的清扫车吸嘴结构进行研究;文献[8]中提出用正交试验方法来进行多因素、多水平对指标的影响研究;文献[9]针对旋风分离器多结构参数的变化,以回归正交试验法为试验方案,建立了回归数学模型,确立了影响分离效率的主要因素;文献[10]利用正交试验进行试验,分析了各因素对气固两相流能耗的影响。上述研究中试验工作量大,集中采样数据点多,试验求解只能评价影响因素主次,未能全面考虑影响因素及各种影响因素的取值范围。
径向基神经网络(radial basis function neural network ,RBFNN)具有较好的鲁棒性及容错性等优势,被广泛应用到预测、控制等领域[11]。文献[12]提出了一种基于粒子群优化RBFNN的锂离子电池健康状态(SOH)预测方法;文献[13]提出了一种基于RBFNN的过载加速度的预测方法;文献[14]提出了一种以RBFNN为模型的多步预测控制方法。此外,文献[15]提出了一种基于熵的神经网络模型,采用分配熵无序指数以获取参数的变化;文献[16]提出了一种基于熵的人工神经网络的混合算法,熵单位指数作用于调整多层人工神经网络模型的输入。
综上所述,本文针对多因素作用下垃圾颗粒驻留时间预测难的问题,考虑固相、气相和结构三类因素,运用拉丁超立方试验方法[17]获得试验样本,采用基于熵值法的RBFNN预测模型分析上述三类因素对垃圾颗粒驻留时间的影响;在垃圾颗粒驻留时间预测问题中,颗粒直径、吸尘负压等因素的变化会对预测结果产生干扰,因此,在输入数据扰动量中采用熵值法求解的因素权重,以提高预测精度。
1 影响因素分析
1.1 吸尘口结构
本文以清扫车单吸式吸尘口为研究对象,吸尘口由滚刷、壳体、吸尘管、超声波传感器、进气口和出气口等组成,吸尘负压可调,如图1a所示。吸尘口工作原理如图1b所示,路面垃圾颗粒在滚刷作用下由进气口运动到壳体内,吸尘管连接风机,吸尘口内的垃圾颗粒在负压气流的作用下,从出气口吸出。在工作过程中,吸尘口吸拾垃圾颗粒的性能直接影响清扫车的吸尘效率。
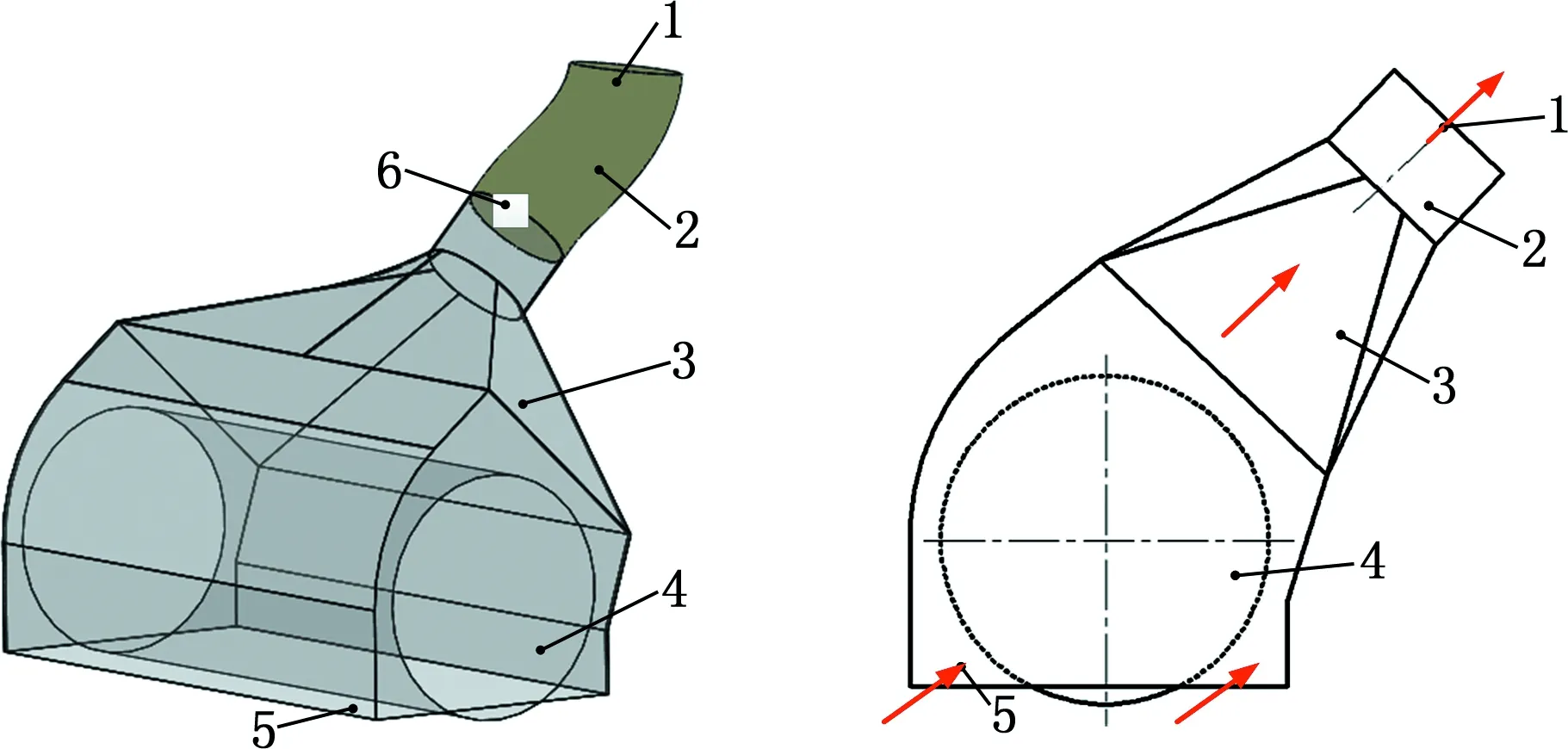
1.出气口 2.吸尘管 3.壳体 4.滚刷 5.进气口 6.超声波传感器 (a)吸尘口模型 (b)工作示意图图1 单吸式吸尘口结构Fig.1 Structure of the single suction port
1.2 垃圾颗粒驻留时间的多因素预测模型
影响垃圾颗粒驻留时间的因素按作用机理分为固相、气相和结构三类。其中,固相类因素取决于垃圾颗粒的属性及分布特性;气相类因素受到吸尘装置工作参数的影响,吸尘负压对腔体内压力和速度分布有决定性作用,滚刷转速间接作用于腔体内的流场,且两者共同作用时,与流场速度之间成非线性关系[18];结构类因素取决于吸尘口的结构参数,影响能量损耗、流场分布。
基于以上影响参数,建立垃圾颗粒驻留时间T关于空间位置(x,y,z)的多因素模型:
T(x,y,z)=T(X1,X2,X3)
(1)
X1=(x11,x12,x13)T
X2=(x21,x22,x23)T
X3=(x31)T
式中,T为垃圾颗粒驻留时间;X1为固相类因素;x11为颗粒密度;x12为颗粒直径;x13为颗粒流量;X2为气相类因素;x21为吸尘负压;x22为滚刷转速;x23为环境温度;X3为结构类因素;x31为吸尘管直径。
垃圾颗粒驻留时间T是由不同影响因素条件下的仿真模拟值或试验测试值组成的训练样本集,通过本文提出的基于熵值法的RBFNN算法,求得给定影响因素下的预测值。
2 基于熵值法的RBFNN算法
熵值法可用来判断指标的离散程度,离散程度越大,对指标综合评价的影响越大。同时,RBFNN具有最佳逼近性能和全局最优特性,能通过大量离散点逼近未知的非线性函数,可实现对垃圾颗粒驻留时间模型的预测,因此,本文提出基于熵值法的RBFNN预测方法来分析三类因素共同作用下的垃圾颗粒驻留时间。
2.1 熵值法求解多因素权重[19]
为了分析各因素变化对垃圾颗粒驻留时间的影响,采用熵值法求解n个试验点对应的因素权重,具体步骤如下。
(1)计算每个试验点中单个因素占全部试验点中该因素的比重:
(2)
式中,zij为第i个试验点的第j项因素的影响程度。
(2)分析第j项因素的熵值:
(3)
(3)计算信息熵冗余度:
gj=1-ej
(4)
(4)计算各因素的权重:
(5)
2.2 添加权重扰动的RBFNN算法
对试验点矩阵添加扰动,建立基于熵值法的RBFNN预测模型。RBFNN模型表示为(m-g-1),其中,各因素作为输入层,输入层的节点为m个;隐含层的节点为g个;垃圾颗粒驻留时间为输出层,输出层的节点数为1。
定义由n个试验点组成试验点矩阵Yn×m;在n个试验点中选l个试验点组成矩阵Yl×m,将该矩阵作为训练神经网络模型的输入值,对应的垃圾颗粒驻留时间试验值ti作为输出值。剩余的h(h=n-l)个试验点组成矩阵Yh×m,将该矩阵作为预测模型的输入值,对应的垃圾颗粒驻留时间预测值ui作为输出值,得到RBFNN模型的输出误差:
(6)
式中,h为预测试验点个数。
调整神经网络模型的预测精度的步骤如下。
(1)由式(5)求得影响吸拾性能的多因素初始权重后,对l个试验点组成的矩阵Yl×m添加扰动,生成扰动试验点矩阵:
(7)
P=(1,1,…,1)T
V′=V+α
(8)
α=(α1,α2,…,αm)
V=[V1V2…Vm]
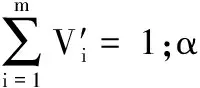
(9)
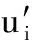
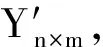
(10)
式中,r为离差设定值。
通过寻找扰动试验点和原试验点的离差极小值,以保证此算法的可靠性;利用模型输出误差保证基于熵值法的RBFNN模型的预测精度。
3 吸尘口试验分析
3.1 影响垃圾颗粒驻留时间的因素分析
影响垃圾颗粒驻留时间的3类因素及取值范围见表1,其中,固相类因素个数a取3,气相类因素个数b取2,结构类因素个数p取1。

表1 因素类型及范围
根据太原市道路垃圾直径、类型及分布密度选择颗粒直径、颗粒密度及颗粒流量[20];根据清扫速度在3~20 m/s的中型清扫车的滚刷转速及风机风压选择滚刷转速和吸尘负压;结构类因素选择吸尘管直径,吸尘管直径取值范围依据吸尘腔内的压力损失及平均气流速度来确定[21]。依据上述因素类型及范围设计吸尘口试验,并获取试验点矩阵Yn×m,分别以仿真试验[22]和测试试验两种方法求解垃圾颗粒驻留时间ti(i=1,2,…,n)。
3.2 吸尘口仿真模拟试验分析
仿真模拟试验采用拉丁超立方试验方法,设计包含6个影响因素的100个试验点。采样空间分为3层,每层横/纵坐标各代表1个影响因素;将各影响因素的取值范围等分成100个区间,则每层可得到100×100个子域;再在各子域中随机抽取1个点,将这些点取整组成一组向量作为影响因素的样本;将样本代入吸尘口仿真模型中得到气相流场特性和垃圾颗粒运动轨迹。
以其中1个试验点仿真结果为例进行分析,该试验点的输入影响因素如下:颗粒直径d为1 mm,颗粒密度ρ为1 200 kg/m3,颗粒流量q为50 g/s,滚刷转速nr为450 r/min,吸尘负压ps为3.5 kPa,吸尘管直径D为110 mm。
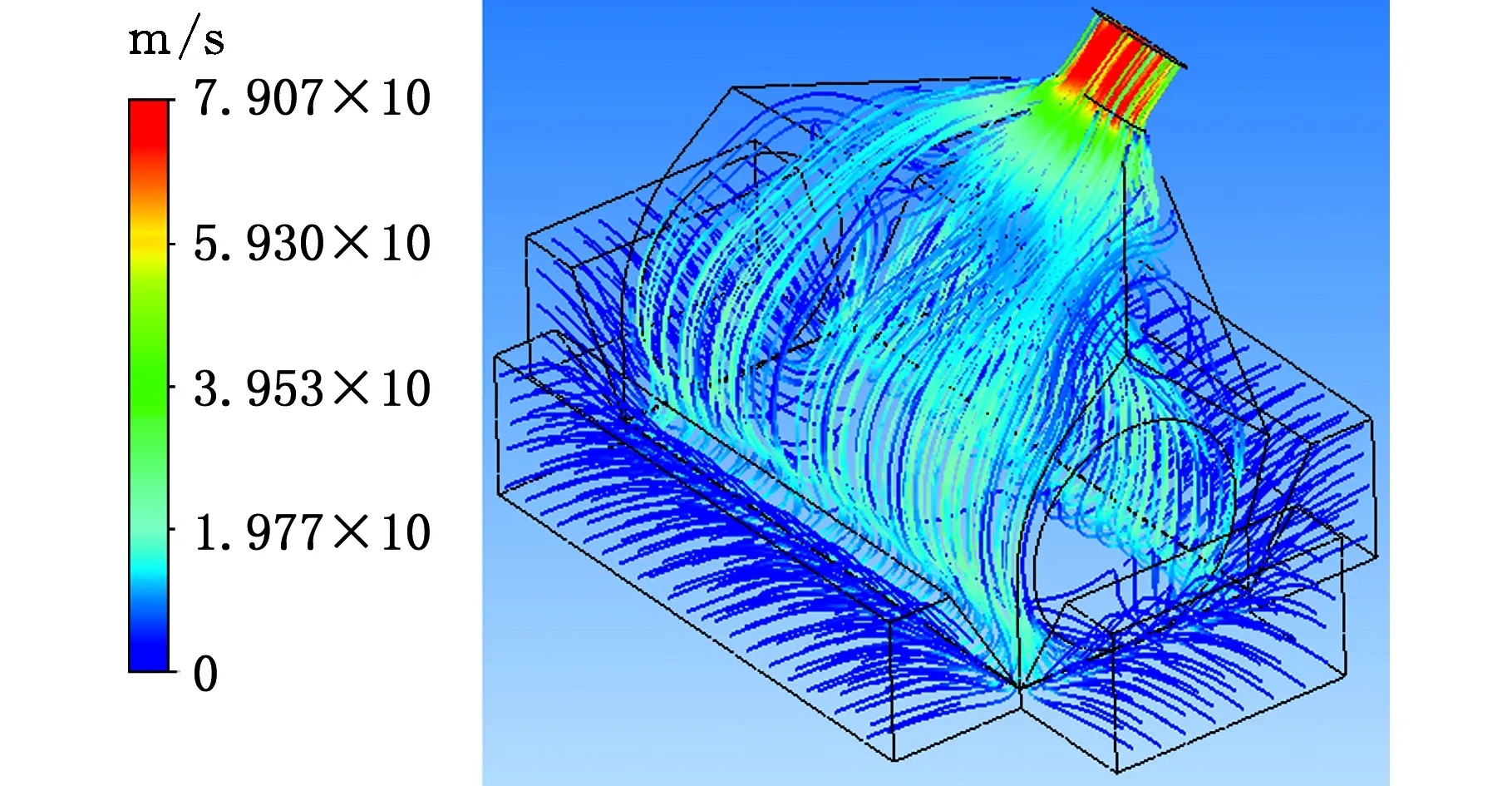
图2 吸尘腔体内的气体流线Fig.2 Gas flow in the suction chamber
吸尘腔内的气体流线仿真结果见图2。外界气体受到腔内负压的作用,从吸尘口底部进入,绕过滚刷的气流由吸尘腔到达吸尘管。由于吸尘腔两侧气流向上的运动被壳体限制,气流向中间运动,与绕过滚刷的其他气流相撞,因此,在滚刷两侧上部位置产生涡流。由图2可以看出,吸尘管附近的平均气流速度为35 m/s,达到了吸拾垃圾颗粒的最小速度,因此吸尘腔内的垃圾颗粒在气流的带动下从吸尘管排出。
垃圾颗粒在吸尘腔内的运动轨迹见图3,可以看出,垃圾颗粒通过滚刷刷毛获得初速度后,两侧的垃圾颗粒受到腔体内涡流的作用与腔体发生多次碰撞,而中间的垃圾颗粒在速度较高气流的作用下直接由吸尘管排出。由图3可知颗粒不同时刻在腔体内的位置,从而可大致判断颗粒在吸尘口中的驻留时间。
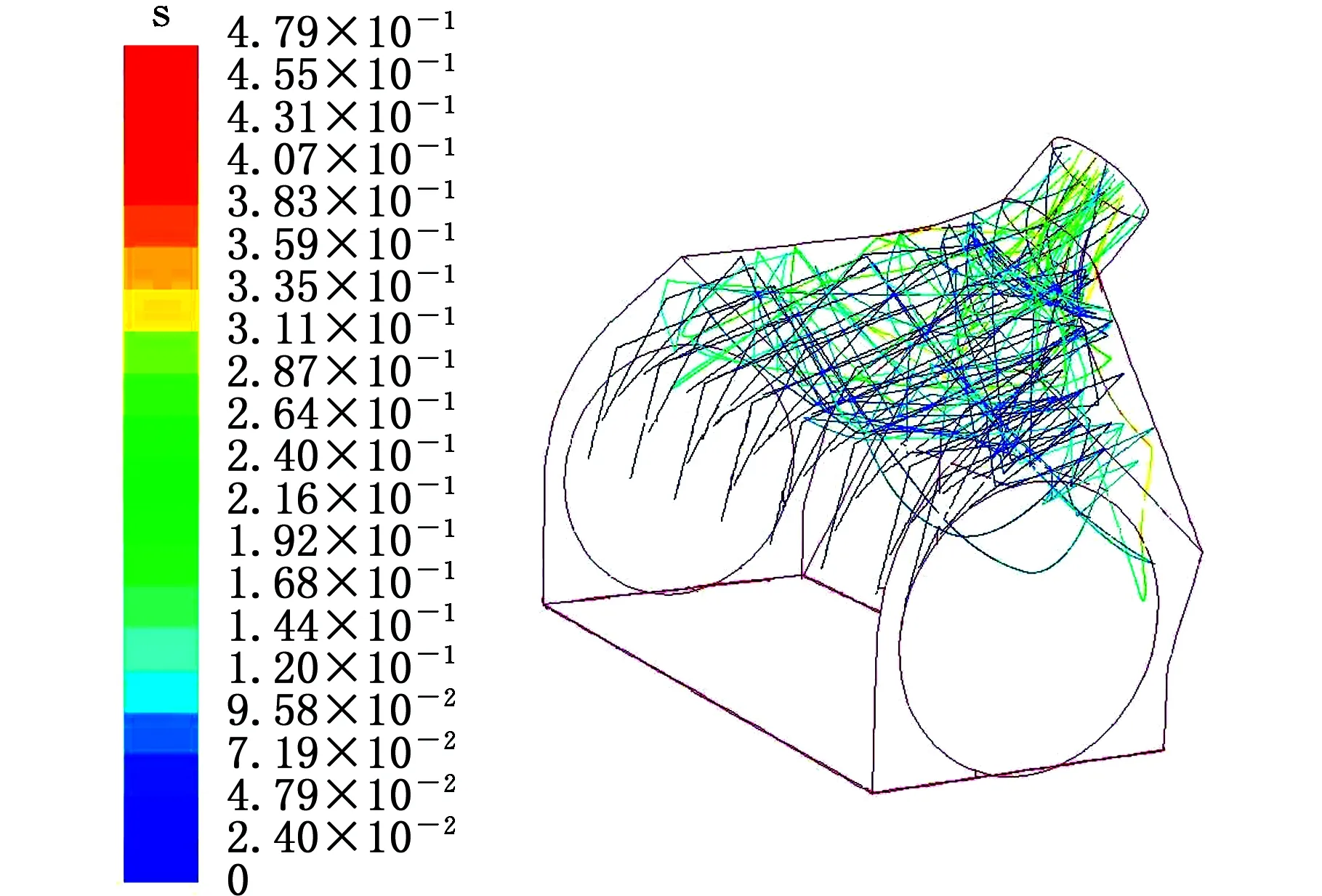
图3 垃圾颗粒运动轨迹Fig.3 Trajectory of waste particles
采用熵值法的RBFNN算法对仿真试验结构预测分析的具体迭代过程如下。
(1)将100个试验点组成矩阵Y100×6,选取其中80个试验点组成矩阵Y80×6,其余20个试验点组成矩阵Y20×6。将矩阵Y80×6作为训练神经网络模型的输入值,垃圾颗粒驻留时间试验值ti作为输出值;将矩阵Y20×6作为预测模型的输入值,垃圾颗粒驻留时间预测值ui作为输出值。
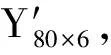
(4)将矩阵Y20×6及对应的垃圾颗粒驻留时间ui作为RBFNN模型的预测值,依据迭代终止条件(式(9)),判断模型精度是否满足条件,若不满足,则返回步骤(2);若满足,则可执行下一步。
3.3 吸尘口测试试验分析
在自主研发的清扫车吸拾性能试验台上进行了吸尘口垃圾颗粒驻留时间的测试试验,如图4所示。该试验台能模拟清扫车吸尘装置工作,吸尘电机额定功率为4.0 kW,风机全压为7 kPa,滚刷电机功率为0.6 kW,滚刷额定转速为900 r/min。采用滚刷电机控制器调节滚刷电机转速,以使滚刷转速与仿真边界条件中的滚刷转速保持一致。采用吸尘电机控制器调节吸尘电机转速,以使吸尘管的吸尘负压与仿真边界条件中的吸尘负压保持一致。

(a)整体结构 (b)吸尘口图4 清扫车吸拾性能试验台Fig.4 Test platform of sweeper pick up performance
数据采集系统由安装在进气口、吸尘腔、出气口、风机进口和风机出口位置的差压变送器,安装出气口位置的超声波传感器,安装在滚刷的激光测距传感器和安装在电机支架上的磁电式转速传感器组成,各传感器的型号及参数见表2。差压变送器用于采集吸尘装置的风压信号,磁电式转速传感器用于采集吸尘电机和滚刷电机的转速。
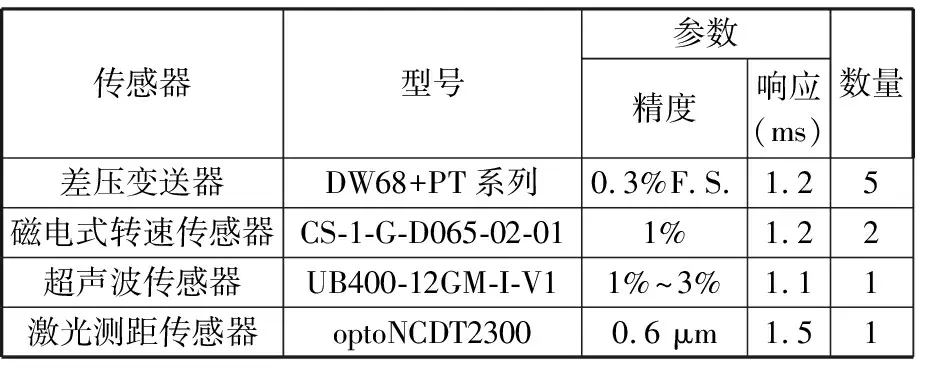
表2 传感器型号及参数
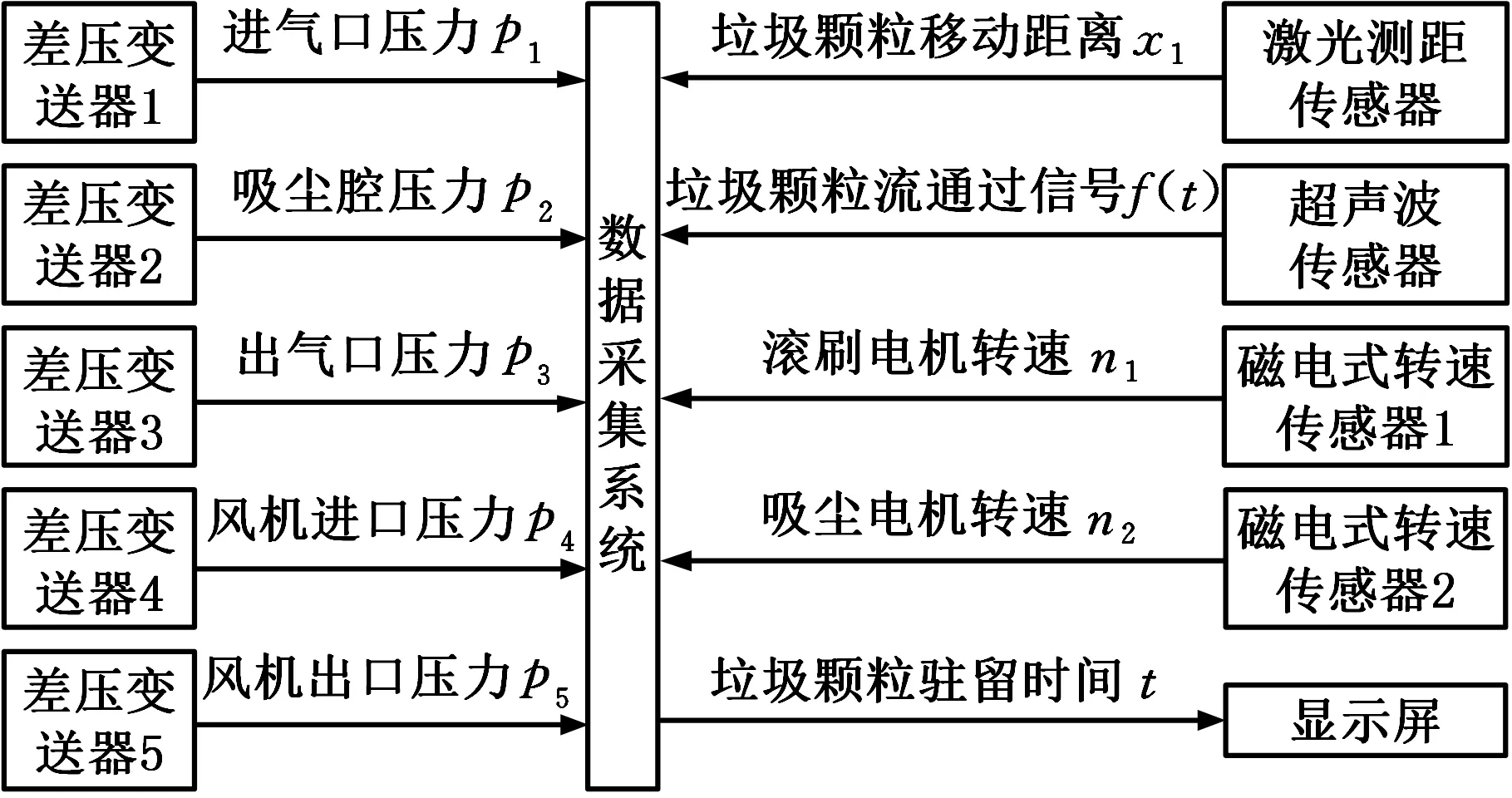
图5 数据采集系统Fig.5 Data acquisition system
数据采集系统接收激光测距传感器、超声波传感器等采集的信号,并输出垃圾颗粒驻留时间,如图5所示。将激光测距传感器测得垃圾颗粒到达滚刷前侧的时刻作为起始时刻,将超声波传感器测得垃圾颗粒流全部通过出气口的时刻作为终止时刻。
测试时,根据各试验点的6个因素值设置试验状态,为了减小试验误差,对各试验点重复测试3次,将所测得的时间取平均值作为测试值,再依次测试得到其余试验点对应的垃圾颗粒驻留时间。
4 结果分析
由吸尘口测试试验得到全部试验点的垃圾颗粒驻留时间后,选取吸尘口测试试验中前80个试验点作为RBFNN预测模型训练样本,剩余20个的试验点作为预测样本。将预测样本所对应的仿真值和测试值进行比较,见图6,可以看出,仿真值与测试值的变化趋势一致,且测试值略大于仿真值,其原因是仿真时不考虑吸尘口漏风等压力损失,导致垃圾颗粒驻留时间偏小。
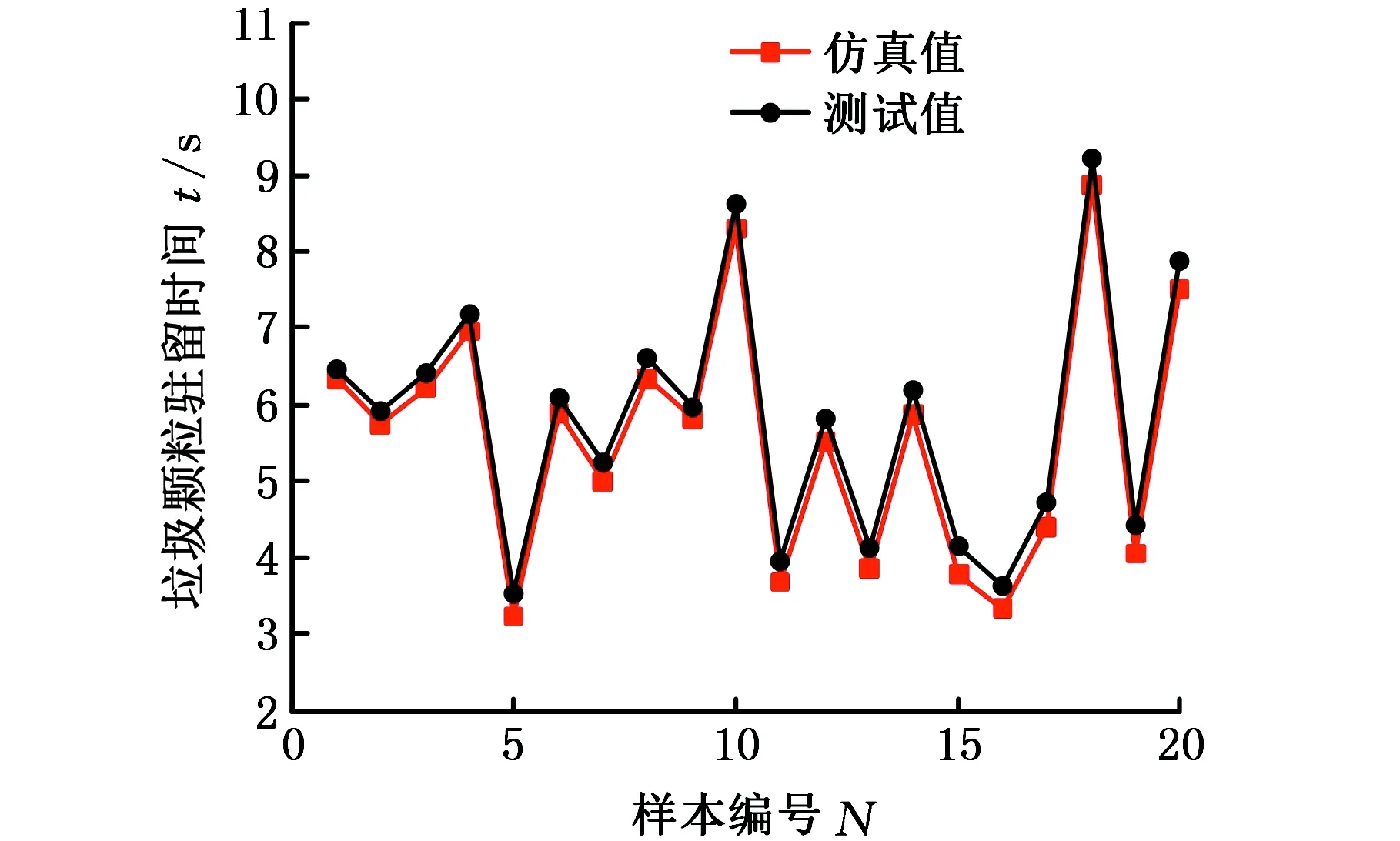
图6 垃圾颗粒驻留时间测试值和仿真值Fig.6 Experiment and simulation values of the residence time of waste particles
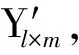
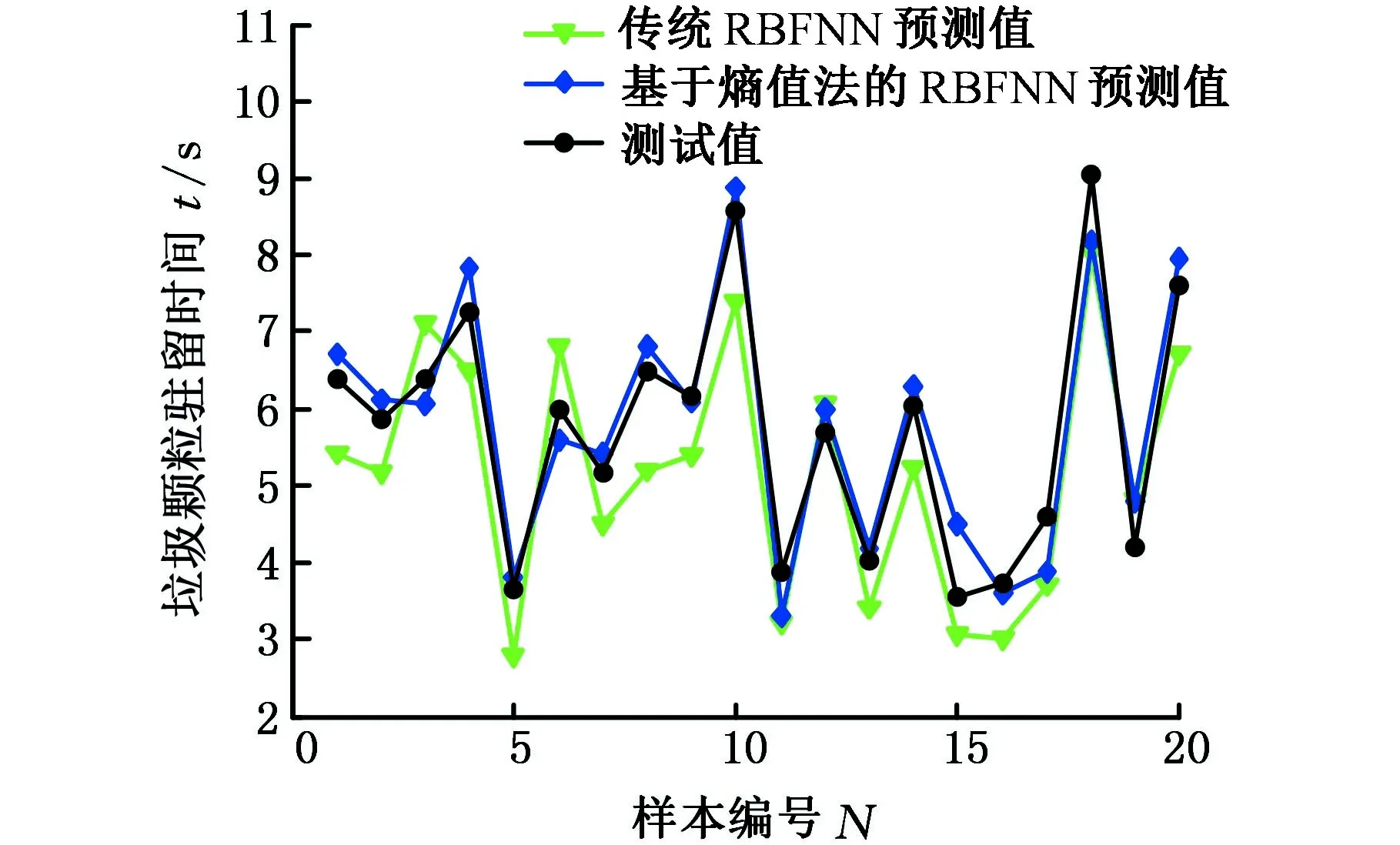
图7 垃圾颗粒驻留时间测试值和预测值Fig.7 Experiment and prediction value of the residence time of waste particles
将基于熵值法的RBFNN预测模型和传统RBFNN预测模型的预测值与测试值进行比较,见图7,可以看出,基于熵值法的RBFNN预测值、传统RBFNN算法的预测值和试验测试值的变化趋势一致。对比测试值与预测值可知(表3),采用传统RBFNN算法的平均误差0.54 s明显大于采用基于熵值法的RBFNN算法的平均误差0.23 s,此外,采用传统RBFNN算法的最大误差1.02 s也大于采用基于熵值法的RBFNN算法的最大误差0.51 s。由此可知,基于熵值法的RBFNN的预测模型具有较高的预测精度。

表3 测试值与预测值对比
5 结论
(1)本文提出了一种基于熵值法RBFNN的垃圾颗粒驻留时间预测方法,该方法考虑了颗粒直径、颗粒密度、颗粒流量、滚刷转速、吸尘负压、吸尘管直径等6个因素,并对试验点进行了垃圾颗粒驻留时间的仿真模拟和试验测试。
(2)与传统RBFNN算法对比可知,采用基于熵值法的RBFNN算法进行吸尘口垃圾颗粒驻留时间预测,其预测值的平均误差与最大误差均小于传统RBFNN算法预测值的平均误差与最大误差,因此所提方法具有求解精度高的优点。
(3)所提方法有助于解决吸尘口垃圾颗粒驻留时间预测不准确的问题,为提高清扫车吸尘口优化设计提供参考。
