可重用零件特征的快速设计技术
2018-12-19程筱胜李大伟孙登广孟令尹
张 壮 程筱胜 戴 宁 李大伟 孙登广 孟令尹
南京航空航天大学机电学院,南京,210016
0 引言
快速设计与制造可有效缩短产品开发周期,提高企业市场竞争力。在设计方面,约80%的设计为变型设计和自适应设计[1],即大多数设计过程是基于以前设计知识的重用,有效利用设计知识的重用可支持快速设计。设计重用有着不同的层次与类型,人们对设计重用的理论及实践进行了许多探索,研究集中在产品的几何、拓扑、特征信息的表达与检索以及基于现有三维建模软件的二次开发,存在对平台依赖性大、设计重用在工程实际中应用困难的问题。几何信息作为产品或零件的最基本信息,是设计重用的最基本内容。
计算机处理速度不断加快,增材制造几乎可以制造任意复杂程度的形状和结构,在此背景下,网格直接编辑建模方法不断发展,从而拓宽了设计空间,其中利用设计重用思想的网格融合技术优势最为明显。网格融合可将各种现存的任意复杂的数字化特征模型按照某种方法组合在一起,创造出新模型。这为零件的设计重用提供了新思路。大多数零件(尤其是复杂零件)都可以认为是由多个不同特征组合或者“装配”在一起的。此处特征是指面向设计过程从构造零件的结构和功能出发提取出具有一定形状的几何体。特征可以是简单几何体,也可以是具有一定功能的复杂几何体。对于系列化零件,常用的几个特征如果可以在新零件设计过程中直接“装配”在基体上,那么设计效率将会有很大提升。通过对现有模型的特征分解,进而对特征利用网格融合技术进行再设计,可有效实现设计知识的重用。
网格融合技术主要分为两类。第一类方法采用网格过渡融合方法实现特征网格在目标网格上的粘贴。该类方法不需要对网格进行整体变形,而是使特征网格和目标网格之间光滑过渡。SINGH等[2]提出采用过程隐式曲面来连接多面体的新方法,但该方法要求融合区域为星形,许多情况下并不能满足;缪永伟等[3]对特征网格和目标网格的边缘曲线之间进行Hermite插值得到拼接连续曲面,然后对其进行三角网格化以及Laplacian光顺处理,但其方法交互复杂。第二类方法的主要思想是对特征网格进行整体变形,使之适应目标网格的形状。 BIERMANN等[4]提出一种基于半规则多分辨细分曲面将特征网格剪切到目标区域的方法,通过直接对特征网格和目标区域参数化将特征网格边界环映射到目标网格,但该方法对特征网格和目标区域的复杂度有较强的依赖性,不适合复杂模型间的融合;TAKAYAMA等[5]提出的GeoBrush方法采用自动生成的网格笼子包围替换网格进行变形操作,可能使替换部分的网格出现过度变形或畸变现象。
现有的网格融合技术在艺术造型上有较好的实用价值,但因精度难以满足要求而无法应用在工程领域。为了将网格融合技术应用在零件的设计建模上,并有效控制融合精度,本文提出如下方法:利用离散指数映射(discrete exponential mapping,DEM)参数化方法建立特征网格边界与基网格目标区域的映射关系,提出基于层的网格变形优化算法,减小特征网格畸变,并进一步对网格体积收缩膨胀进行有效控制,最后通过添加几何约束控制网格位置形态。
1 技术路线
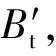
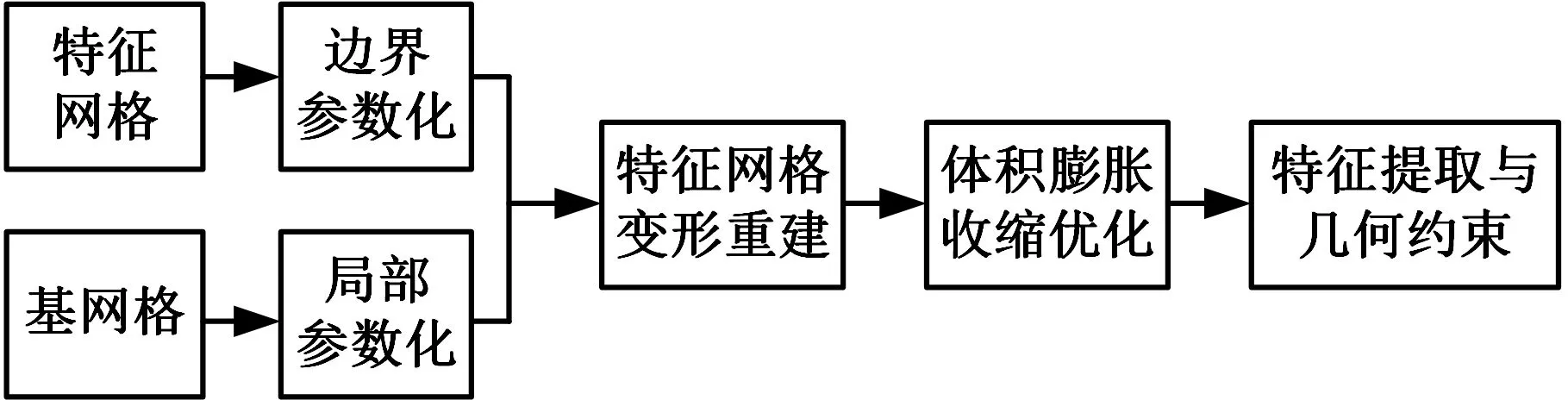
(a)技术路线
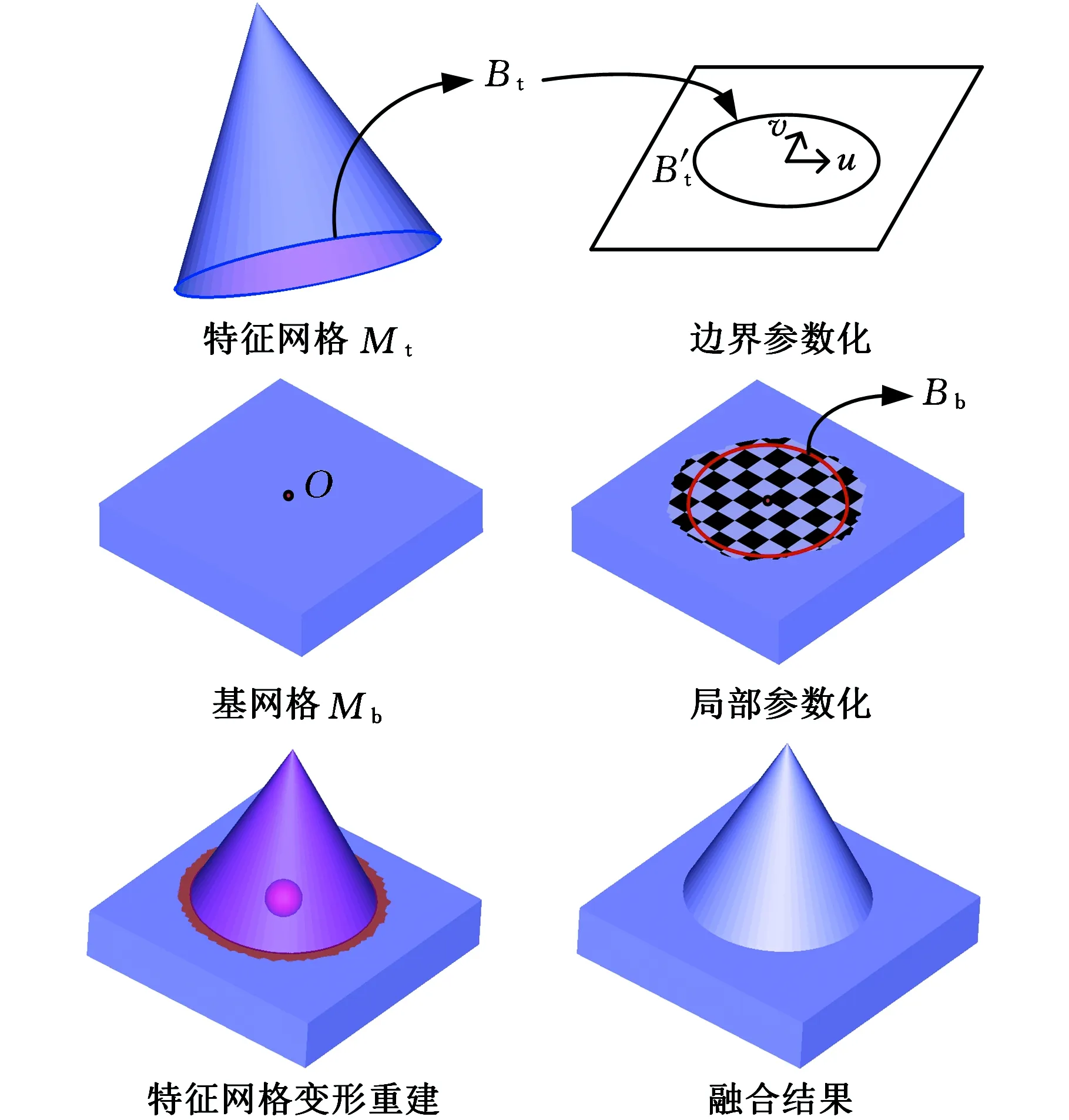
(b)流程示意图图1 技术路线及流程示意图Fig.1 Technology roadmap and flow diagram
2 网格融合建模
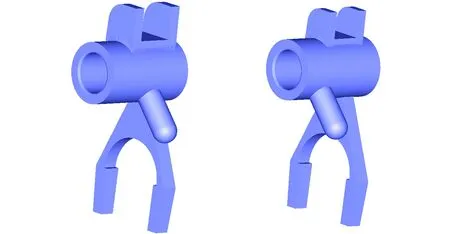
大多数零件由不同的特征组合而成,包括描述零件的基本几何形体的主特征(也称为“基特征”)和多个功能性的辅特征。因为特征重用一般指对具有特别结构和功能的辅特征的设计重用,故文中不作特别说明时特征均指辅特征。对于图2a所示的一个典型拨叉零件,根据零件的形状和功能进行特征分解,包括主特征空心圆柱Base和三个功能性辅特征Part1、Part2、Part3,如图2b所示,其中Part3为一个较为复杂的叉型结构。对图2a拨叉零件来说,网格融合建模就是实现多个具有不同功能的辅特征Part1、Part2、Part3分别与基特征Base的有效融合,即对拨叉零件进行重建,且实现Part1、Part2、Part3在新模型设计中的重用。
2.1 基于DEM的目标区域局部参数化
为建立特征网格边界与基网格上目标区域之间的映射关系,需要对基网格进行局部参数化。本文采用SCHMIDT等[6]提出的DEM方法,该方法是一种局部参数化方法,具有速度快、可有效满足实时交互需求的特点。对于在网格曲率变化大的情况下产生较大畸变的问题,采用路径加权策略和法矢光顺的方法优化[7],可有效减小畸变。
2.1.1指数映射
如图3a所示,在曲面S:r=r(u1,u2)上取定一点P,任取切向量v∈TP,作测地射线CP,v从P点出发,且以v/|v|为初始切向,则CP,v由P和v/|v|唯一确定。取CP,v的正向弧长s参数化ui(s),i=1,2,使P点在S上的曲线坐标为(u1(0),u2(0))。定义映射
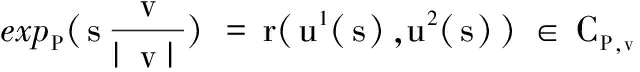
即像点Qs=r(u1(s),u2(s))是CP,v上从点P出发而经过弧长s所到达的点。由此定义映射
expP:v⊂TP→S
v→expP(v)
则此映射称为曲面S上点P处的指数映射[8]。

2.1.2离散指数映射参数化
对于网格曲面,为得到曲面S上点p处的指数映射,需要计算网格上其他点q的测地线距离与极角,进而得到测地线向量。对于种子点P的一环邻域点,测地线距离就是两点间距离,所以很容易得到一环邻域点的测地线向量,但是对于k-ring邻域(k>2)的情况,测地线的计算耗时巨大,不能满足实时交互的要求。离散指数映射参数化方法[6]采用近似策略,通过由Dijkstra算法[9]产生分段线性测地线向量的叠加来代替直接计算点q到点p的测地线向量,有效减小了计算量。
如图3b所示,假设网格曲面上有3点p、r、q,容易得到点r在切平面Tp上的测地线向量up,r和点q在切平面Tr上的测地线向量ur,q,而up,q未知,即点q在切平面Tp上的测地线向量未知。在线性系统中存在:
up,q=up,r+(up,q-up,r)
(1)
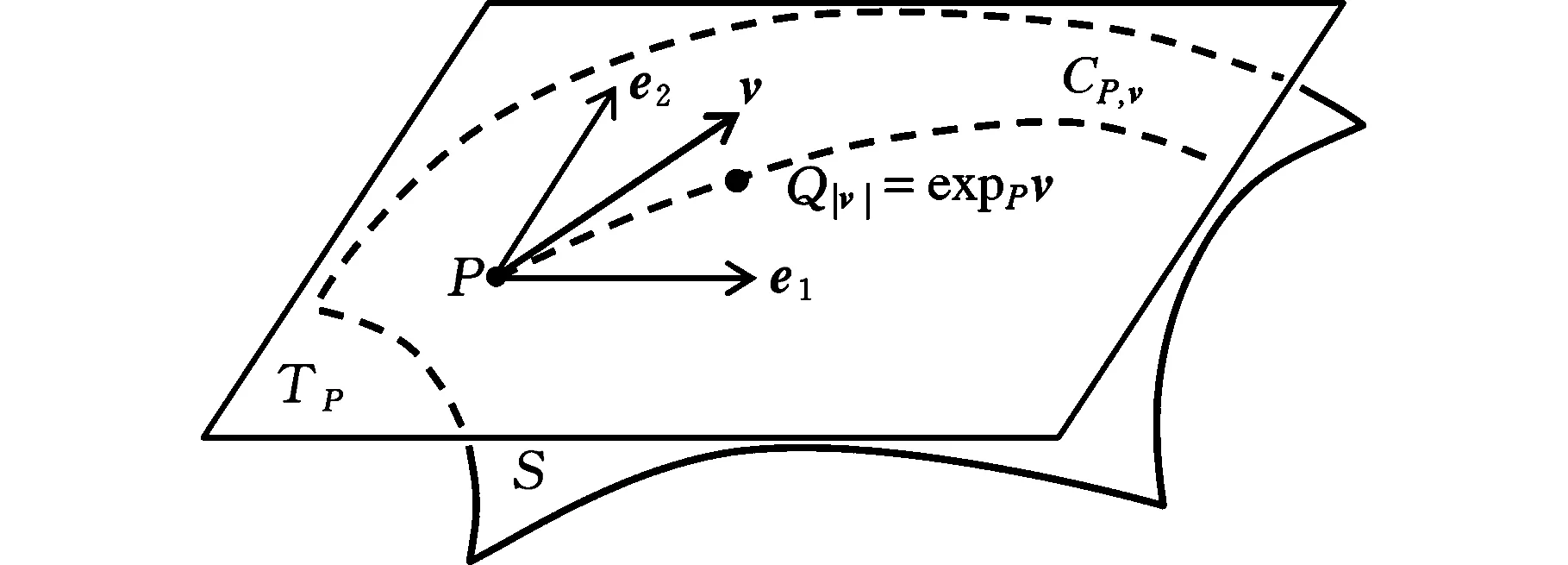
(a)指数映射概念[8]
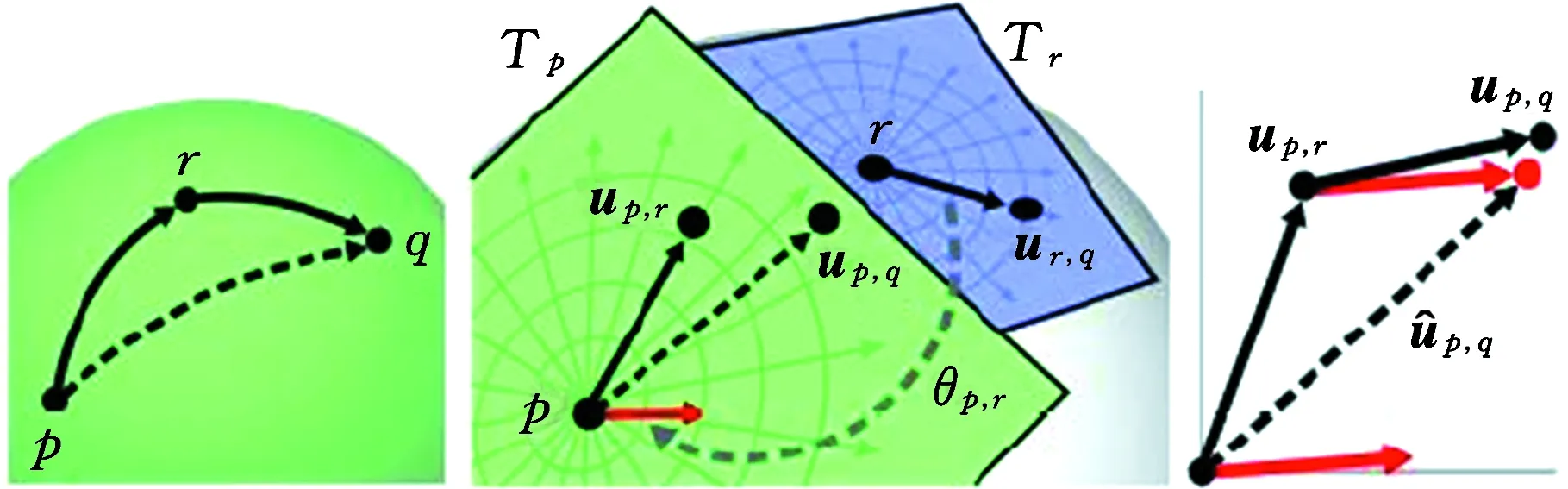
(b)离散指数映射近似[6]图3 离散指数映射参数化Fig.3 Discrete exponential map parameterization
考虑用ur,q的一个相关量来代替(up,q-up,r),首先将切平面Tr中的测地线向量ur,q转换到Tp中,然后进行向量叠加。设Tp和Tr对应的法矢分别为np和nr,首先将nr旋转一定角度使其与np共线,此时Tr和Tp共面,然后将Tr绕着np方向旋转角度θp,r使得两坐标系完全重合。此时Tr上的ur,q就可以用Tp的基底来表示。由于up,r和ur,q都是二维向量,忽略第一次旋转的影响,可以得到up,q的近似值:
up,q=up,r+rot2D(θp,r)ur,q
(2)
式中,rot2D(θ)表示做角度为θ的二维(2D)旋转。
此方法求取的up,q与网格上实际测地线向量值存在误差,但是在只考虑局部参数化的情况下,精度在一定参数化范围内能够保证。对于该方法在曲率变化大或者突变处不理想的情况,采用上层邻域点路径加权和法矢光顺的改进方法[7]。
采用唯一路径求取网格上点的测地线向量会造成累积误差。路径加权策略(即后续扩张点的测地线向量由其上层邻域点加权决定)避免了由某一过大误差对后续点产生压倒性的影响。重新定义up,q:
(3)
(4)
式中,ri为点q的上层邻域点,ri为其坐标向量;q为点q的坐标向量;w为反距离权值。
计算过程中由法矢确定切平面,故法矢对结果有重要影响。对法矢进行光顺(某点处的法矢用该点的k环邻域内所有点的法矢的加权平均值代替)能有效改善曲率变化大的网格区域处的参数化结果,权重函数采用式(4)。
2.2 特征网格边界参数化
针对特征网格边界参数化问题,BIERMANN等[4]提出对特征网格本身进行参数化,但该方法不仅计算量大,需要对整个特征网格进行参数化,而且对于空间结构复杂的特征网格无法有效保持边界的几何信息,误差较大;钱归平等[10]提出垂直投影参数化方法,同样不能有效保持边界信息,导致融合网格畸变严重。本文首先以边界点为约束条件,利用最小二乘网格[11]对特征网格进行补洞处理,进而对补洞网格利用DEM方法进行参数化,得到边界点的参数化结果。
2.2.1最小二乘网格
对于具有n个顶点的三角网格模型(V、E、F)(V、E、F分别表示点集、边集和三角面片集),定义第i个顶点vi的拉普拉斯坐标为
(5)
wij=1/|N(i)|
式中,N(i)为顶点vi的一环邻域点的集合;ki为点vi的平均曲率;ni为单位法向量;vi为vi的坐标向量。
给定光顺条件δi=0,即顶点的平均曲率均为0,通过求解下式得到最小二乘网格:
LV=0
(6)
其中,矩阵L为如下n×n的拉普拉斯矩阵:
(7)
对于一个连通的网格模型,矩阵L的秩为n-1,另给一个顶点的位置约束作为初始条件就可以求得唯一解。在实际应用中,通常引入一组控制点vs=(xs,ys,zs);s∈C,C={s1,s2,…,sm},si为第个i控制点的序号。此时线性系统变成超静定线性系统:
Ax=b
(8)
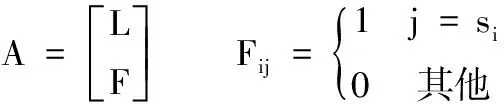
V中y,z分量同理。对式(8)的求解等价于优化如下能量方程:
(9)
对上式利用线性最小二乘法,通过Cholesky分解[12]并回代求出拟合解,得到最小二乘网格[11]。
2.2.2补洞网格参数化
采用补洞法进行边界参数化,主要考虑网格融合过程中特征网格的初始形变条件不仅需要边界点的坐标信息,还需要边界点的法矢信息来构建边界点的局部坐标框架。初始形变条件下,边界点的局部坐标框架与基网格上目标区域边界点的局部坐标框架重合,即两边界点的法矢同向。当特征网格与基网格在边界处平滑过渡时,特征网格边界点的法矢取其本身即可,但对于零件,特征通常是“矗立”在基体之上,此时依然取特征网格边界点法矢本身相当于给定平滑约束,会导致融合网格严重畸变。利用补洞网格边界点的法矢来代替特征网格边界点的法矢则在两种情况下都有较好的结果。
显然,当特征网格的边界在一个平面上时,其参数化结果是精确的。同样,特征网格边界点分布越接近于平面,其参数化结果误差就越小,网格融合效果越好。由此考虑用一个尽量接近于平面的网格进行补洞。如图4所示,对图2中辅特征Part1提取其网格边界(图4b),将边界保边长地映射至一个平面圆上,并将此圆利用Delaunay三角化[13]生成一个二维的补洞初始网格(图4c),指定边界点为控制点生成最小二乘网格(图4d)。图4d就是保持光顺的同时最接近于平面的网格。对图4d利用DEM方法进行参数化,结果见图5。
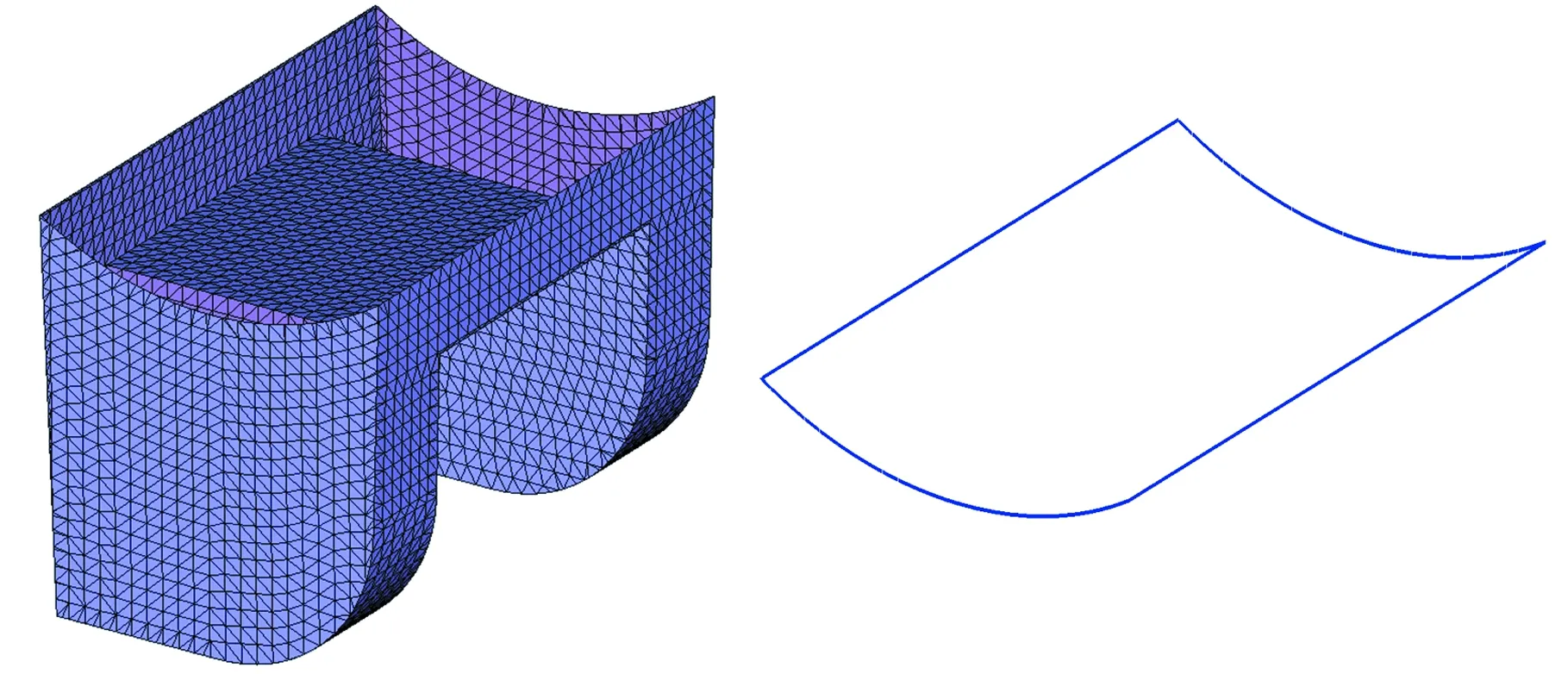
(a)Part1特征网格 (b)网格边界

(c)补洞初始网格 (d)最小二乘网格图4 最小二乘网格补洞Fig.4 Filling holes with least-squares meshes

(a)坐标 (b)边界点法矢图5 特征网格边界参数化结果Fig.5 Results of boundary parameterization offeature meshes
2.3 基于层的网格变形优化算法
三维网格变形的本质就是通过某种映射关系将源网格中的顶点转换到一个新的位置,生成新的网格并保持拓扑关系。在SINGH等[14]提出的基于曲线的变形方法基础上,SCHMIDT等[7]提出了COILS(本文称为“基于层的网格变形”)算法,该算法具有细节保持好的特点。本文在此基础上提出基于层距的距离权值分布优化方法,以得到更优保形结果。
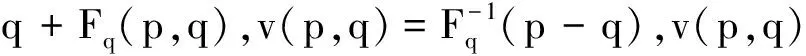
(10)
在变形过程中保证一定刚性的同时也需要具有一定的柔韧度,使初始形变能够较均匀地分布在整个网格上,即保证点p相对于某一区域Ω具有一定程度的刚性即可。对式(10)在区域Ω上积分,有微分表示:
(11)
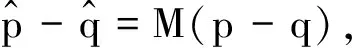
(12)
式中,d为两点间的欧氏距离或测地距离;k通常取2;ε为误差调整值。
对于网格模型,式(11)的离散形式为
(13)
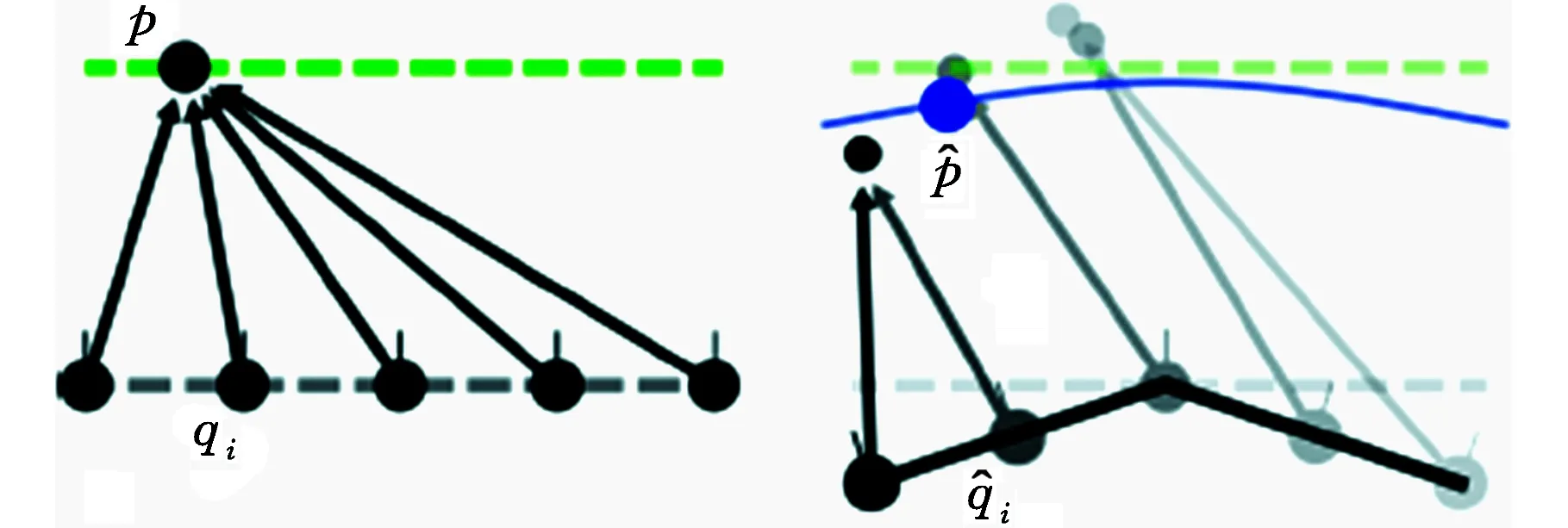
(a)点p随控制点qi的变化而变化[7]
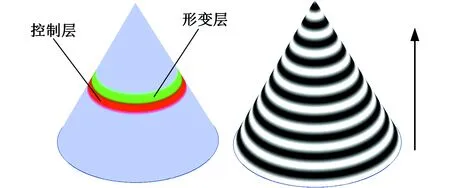
(b)模型分层示意图图6 基于层的网格变形算法示意图Fig.6 Graph of mesh deformation algorithm based on layer
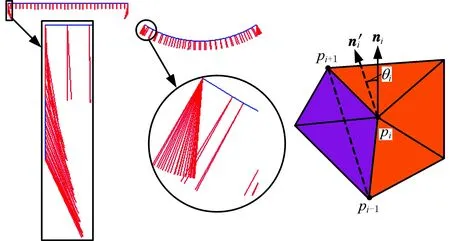
其中,Ω={pi}为线性闭合离散点集。式(13)就是基于曲线变形的表示形式[14],可以看出,采样点的选取和权值函数是变形的关键。选取特征网格边界为Ω,模型上点p远离边界曲线时,基于距离的权值会越来越一致,导致质心下降引起挤压变形,故考虑将曲线的控制范围缩小到一定区域,不同区域用相邻的不同曲线来控制变形,从而减小上述的挤压变形。具体方法如下:从边界线开始对网格模型由下而上进行分层(图6b右),每一层的上一层为该层的控制层,控制层决定着下一层的形变(图6b左)。将每一层看作一条曲线,这种方法类似于基于曲线的变形,变形自边界逐层向上传递,完成整体变形。这里依据测地距离进行层的划分,利用Dijkstra[9]算法近似得到模型上每一点相对于模型边界的测地距离。设任一点pi的测地距离为gpi,层宽为ru(通常取网格模型平均边长的2.1倍),那么控制点pi变形的控制区域(层)为
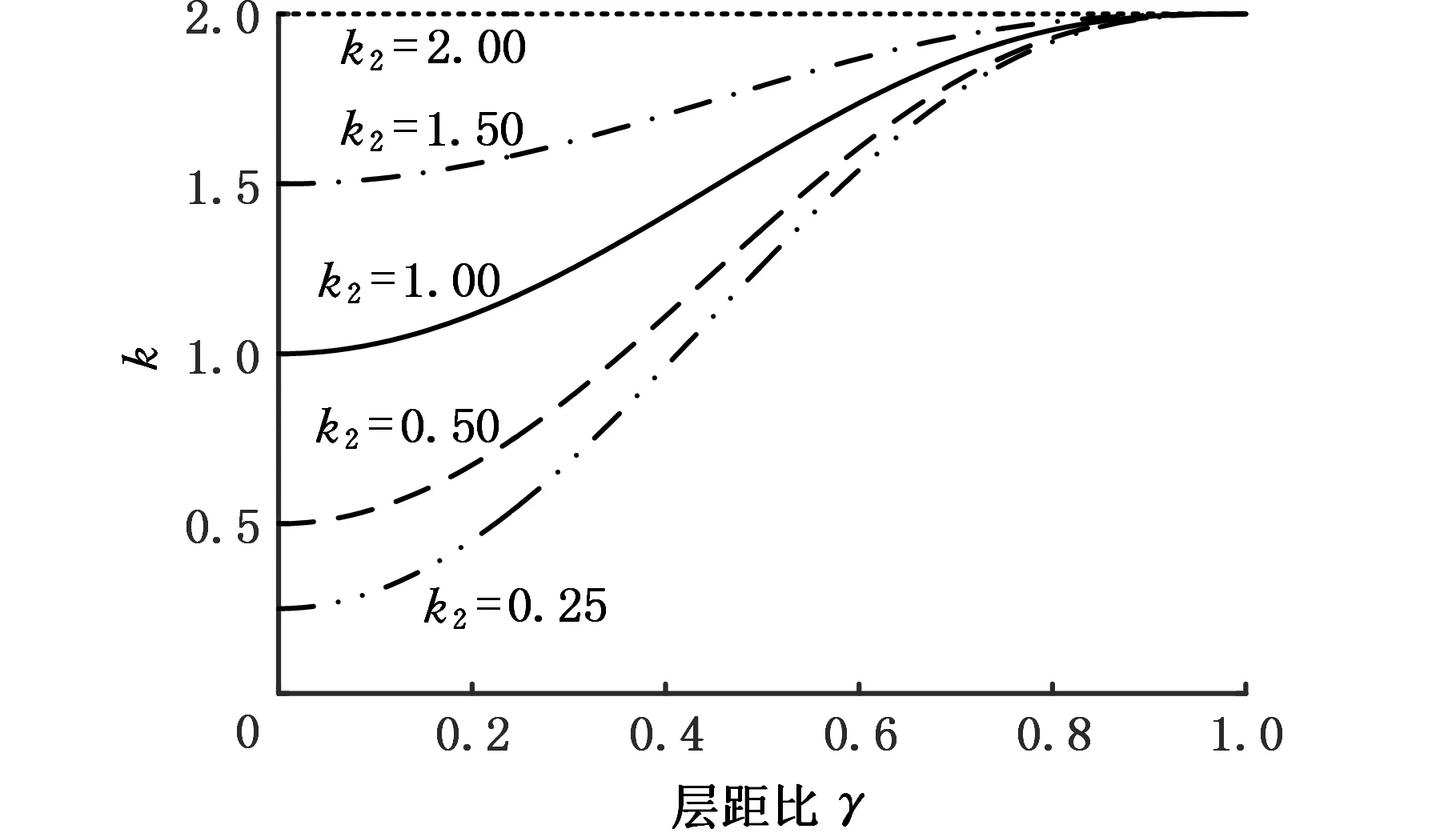
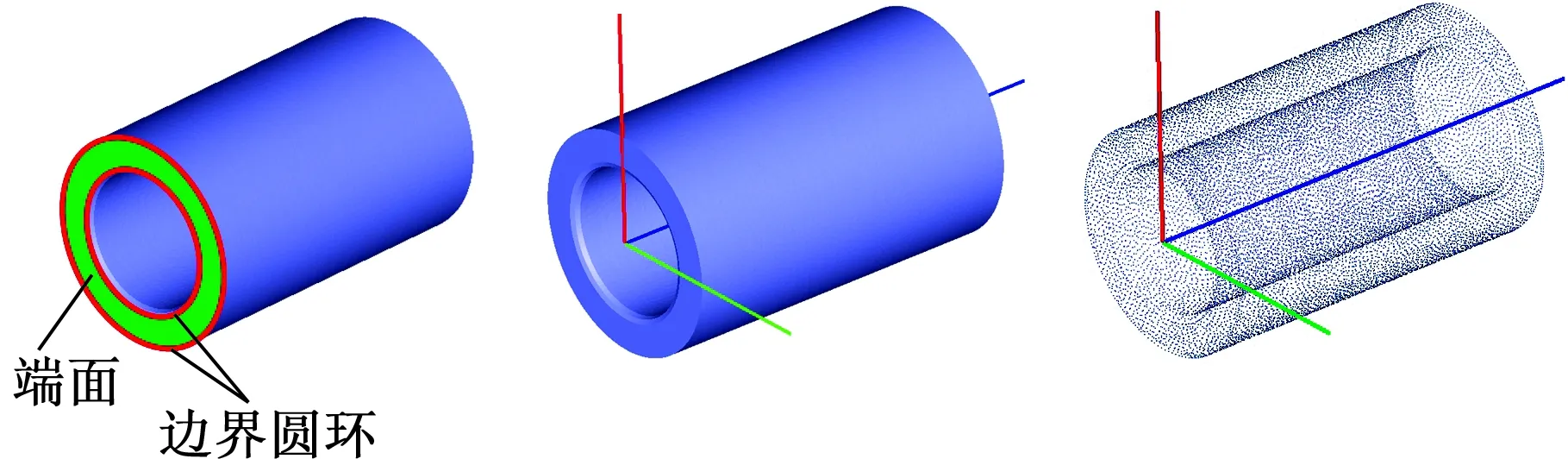
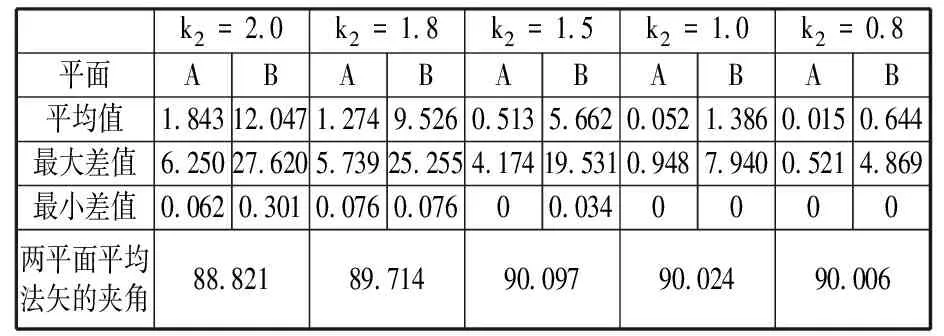
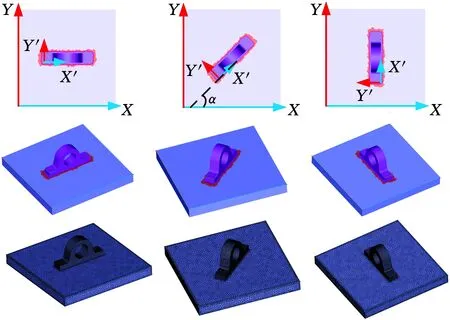
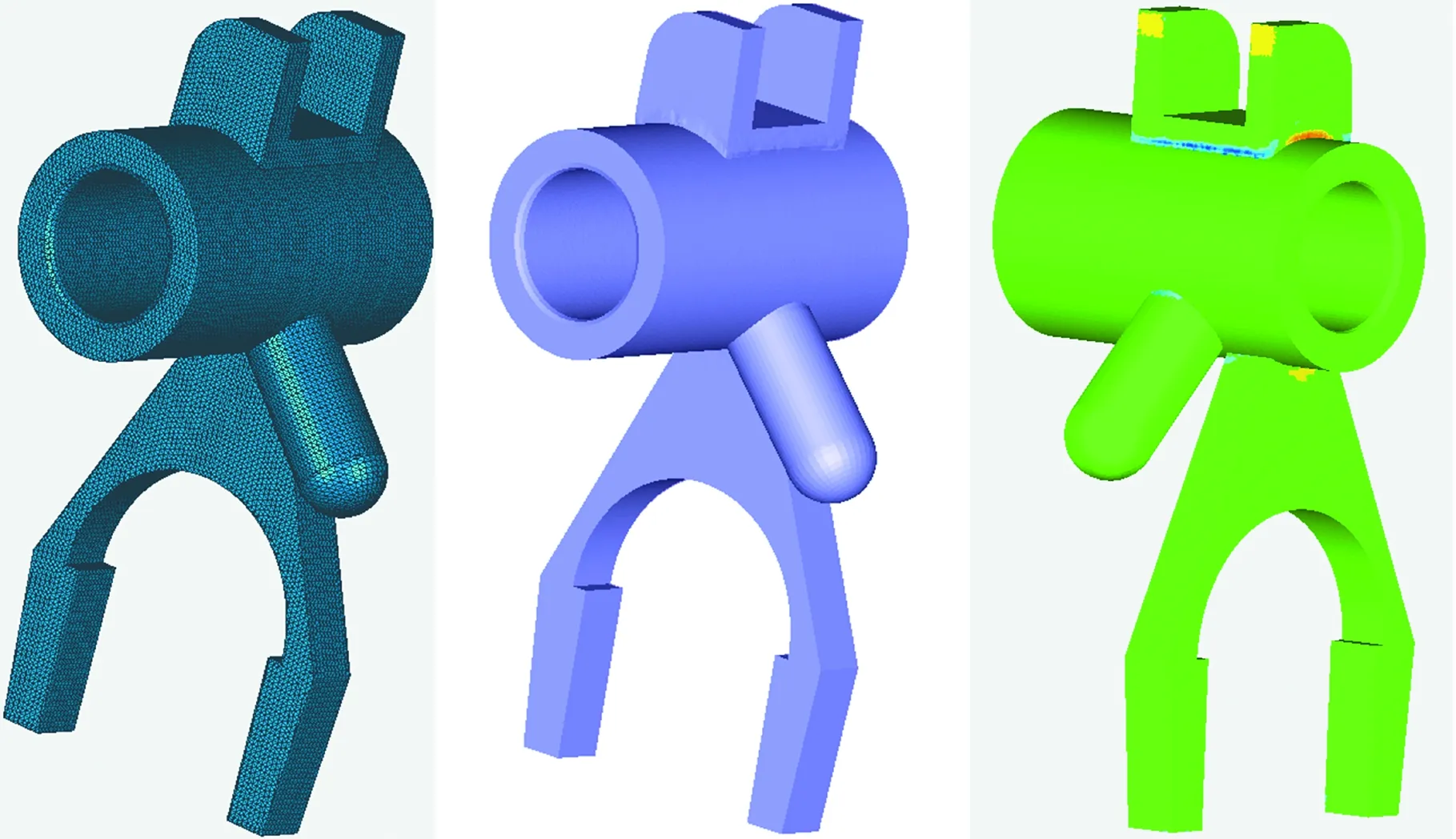
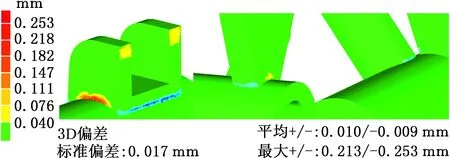
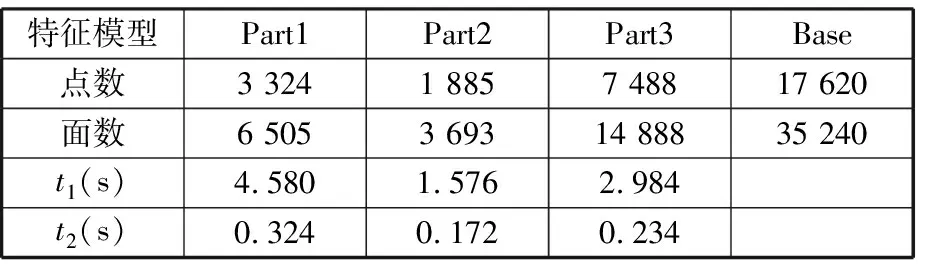
Ω(pi)={pj:gpi-ru (14) 由于权值函数选取为反距离权值,距离点pi越近的点产生的影响越大(其权值接近1),产生压倒性影响,导致变形扭曲,另外在网格比较规则的情况下容易出现不对称变形,因此选用数值从1到0的平滑衰减函数: 引入调节权值 warr(pi,pj)=f(Δg,ru)(1-f(Δg,rn)) (15) 式中,Δg为两点间的测地距离差值;rn为点pi与控制区域Ω内所有点欧氏距离中的最小值。 对细节丰富的网格模型而言,存在不同区域其网格密度不同的情况,同样会造成网格变形向密度较大的区域倾斜。引入面积调节权值 (16) 其中,N(pj)为点pj的一环邻域,Tk为一环邻域内的三角面片;A(Tk)为Tk的面积。wreg即为点pj的一环邻域内所有三角面片面积之和,这样使得采样点在密集和稀疏区域的权值差异不会过大。最终权值定义如下: wup(pi,pj)=warr(pi,pj)wreg(pi,pj)w(pi,pj) (17) 上述变形方法在初始形变较小的情况下具有较好的保形性,但当初始形变较大时,会将形变传递至整个网格,全局保形结果差。对于大多数零件(如焊接件),特征结合处一般为非工作区域,精度要求较低,可以通过对零件特征的分割(即在精度要求不太高的区域进行特征分割)来降低融合边界附近的精度要求。若形变能够较多地集中在融合边界处,同时保证远离边界的网格区域能够具有良好的保形性,那么可以得到更为理想的结果。可以通过调节式(12)中的k值来调整距离权值,使边界附近的点在其控制层中增加距离更近的点的权重,以达到形变集中在边界附近的目的。如图7a所示,当k不断减小,距离权值的分布曲线更加陡峭,形变的分布将更加集中。 如果k值取得过小,将会引起形变的过度集中,导致边界处过渡不自然,甚至出现折叠边等一些网格缺陷;对于远离边界的网格部分,需要更加均匀的权值分布。由此,考虑依据点pi到边界的测地距离di来决定该点的ki值,即随着di的增大,减小ki值。设网格上任意点到边界的测地距离最大值为dmax,引入 ki=k1{1-[1-(di/dmax)2]3}+k2[1-(di/dmax)2]3 (18) 式(18)即是根据di在k1和k2之间进行两端平滑的非线性插值,通常上限k1取2,调整k2的大小就可以得到不同di处的ki值,即在di较小处ki值较小,距离权值分布集中,di较大处ki值较大,距离权值分布均匀。不同k2值下k值随层距比的分布图见图7b,调整k2可以得到整体网格从下到上不同程度的距离-权值分布。 (a)不同k值下距离-权值分布图 (b)不同k2值下k值随层距比变化图图7 基于层距的权值优化Fig.7 Weight optimization based on layer distance 为达到自动控制网格适应性变形的目的,即对于不同的特征网格都能得到相适应的ki分布,考虑量化某一相关量来调整式(18)中的k2值。在2.2.2节中提到,特征网格的边界点分布越接近于平面,其参数化结果误差就越小,网格融合的效果越好,即边界点分布很大程度上决定了初始形变量的大小。在这样的思路下,首先确定一个平面P,使得补洞网格上所有点到平面P的距离平方和最小,设补洞网格上任一点vi到平面P的距离为d(vi,P),P满足下式: P=argmin(∑d2(vi,P)) (19) 式(19)即是用最小二乘法进行平面拟合,对图4d中的补洞网格平面拟合,结果见图8。设补洞网格上所有点到平面P的平均距离为dave,最大距离为dmax1,对k2进行粗略的线性调节(当dave、dmax1都趋向于0时,dave/dmax1取1): k2=c1(dave/dmax1)+c2 (20) 补洞网格本身为平面时,k2取c1+c2,补洞网格相对于平面更加离散时,k2向c2靠近。 图8 最小二乘法对补洞网格平面拟合Fig.8 Plane fitting to filling hole mesh based on least square method 上述变形方法存在网格体积膨胀或收缩的问题,导致特征无法和基网格保持恒定的距离,这在零件的建模中是致命的。解决问题的同时也希望可以在一个较小的范围内通过用户交互指定距离,得到一个可控的弹性的体积变化效果。分析体积变化产生的原因发现,在边界映射对齐过程中,边界点的局部坐标框架重合时产生的影响很大,而局部坐标框架是由边界点法矢来决定的。考虑通过修正边界点法矢来解决体积变化问题以及小范围内控制体积变化。 大量实验表明,在一定程度范围内,边界点的法矢朝向越靠向边界中心,特征网格的纵向膨胀越加明显,反之纵向收缩明显。图4中边界点法矢分布局部放大见图9a,发现法矢大部分朝向边界中心,而该特征的变形重建结果也确实存在体积膨胀的现象。如图9b所示,对于边界上任一点pi,对其法矢ni进行如下修正: (21) 其中,Mθi(pi-1,pi+1)为一旋转矩阵,表示绕轴线pi-1pi+1进行θi角度的旋转,pi-1、pi+1为点pi在边界环上前后相邻两点。为了不造成特征网格的非对称变形,对边界上的每一点都进行同样角度θi的修正。调整θi的目的是保证特征网格与基网格上的某些位置关系,反过来可以通过两网格之间的位置关系(点、线、面等图元的距离或投影距离)来动态调节θi的变化。由于体积变化在适当范围内与θi是成单调增减的,故采用二分法进行迭代逼近,直至满足设置的误差ε要求,表达如下: θ={θi|(dr(θi)-ds)≤ε} (22) 式中,ds为用户指定的两网格某特征图元之间的距离;dr(θi)为在θi角度下融合结果中指定特征图元之间的实际距离。 (a)边界点法矢分布及局部放大(b)法矢修正图9 网格体积变化原因及其修正Fig.9 Reason and correction of mesh volume change 2.5.1局部坐标系的建立 进行网格融合首先需要导入基网格,由于模型来源不同(可能是实体建模导出,或实物重建模型,或其他模型上分割的一部分),故基网格在全局坐标系中形态各异,没有规则。根据基网格本身特征建立一个局部坐标系FL,并计算其与全局坐标系FG的变换矩阵M1,M1满足FG=M1FL,对网格整体V1进行坐标变换,得到指定规则下网格新位置V2: V2=M1V1 (23) 这样不仅为几何约束提供了方便,还有利于后续对模型的切片打印等处理。不同的基网格有着不同的特征,同时面向不同的建模需求可能需要建立不同的坐标系。本文使用交互的方式建立坐标系,选取图2拨叉零件的基特征Base(一个空心圆柱)予以简单说明,如图10所示。首先通过选取端面上任一点向外扩张,依据法矢差异大小作为扩张停止条件,得到整个端面以及端面两边界圆环(图10左);其次对两边界圆环分别利用最小二乘法进行空间圆拟合,分别求出两圆心位置并求平均值,作为坐标系的原点;然后对端面所含面片集求平均法矢作为z轴,原点与端面上任一点共同决定x轴,y轴由x、z轴确定。所建坐标系如图10所示。 图10 建立局部坐标系Fig.10 Construct local coordinate system 2.5.2特定图元提取与添加几何约束 添加几何约束需要拾取特定的图元(点、线、面等)。如上所述,可以依据法矢或者曲率对网格进行简单的分割,得到不同面、面面相交的特征线以及线的各端点。对离散的面和线拟合以得到具体几何信息。 特征网格在基网格上的位置形态完全由两者的参数映射决定,因此通过确定参数域中心可以确定位置,确定参数域的缩放比例(同时对特征网格进行等比例缩放)可以确定大小,确定参数域的二维旋转变换可以确定朝向。实体建模中几何约束理论成熟,对提取的特定图元进行类似约束(如点面距离、面面平行等),最后反求出参数域中心和二维旋转变换,得到最终带位置约束的融合结果。 本文算法采用C+ +语言在VS2008平台及OpenGL函数库下实现,PC机配置为CPU i5-4460、3.20GHz,内存4GB。 选取图2拔叉零件中特征Part1和Base作为实验模型,见图11a,利用2.3节算法,随着k2值不断减小得到图11b所示的变形结果,其中k2=2.0时的结果也就是SCHMIDT等[7]的结果。直观上看,随k2不断减小,特征网格的形变从全局慢慢集中到边界附近,而远离边界处的细节高度保形。 为准确衡量特征网格的保形性,取图11a中的A、B两平面分析其平面度和垂直度,具体见表1,最后一组k2=0.8是通过2.3节中所述方法自动计算的结果。表1中,平均值指面的平均法矢与各顶点法矢夹角的平均值,最大、最小差值指平均法矢与各顶点法矢的最大夹角和最小夹角。A包含423个顶点,747个三角面片;B包含483个顶点,880个三角面片。显然,k2=0.8时A、B保形程度很高。 表1 特征网格保形性分析 同样选取图2拔叉零件中特征Part1和Base作为实验模型,在基于层的网格变形优化之后,采用2.4节中体积控制方法,在k2=0.8、ds=10.0、ε=0.02的条件下,得到图12d所示的控制结果。为反映体积随角度θ变化而变化的趋势,给出不同θ下的网格形变结果,见图12。θ取值以及衡量网格体积变化的dr值见表2,其中θ取负值表示朝背向边界中心的方向调整边界点法矢。 (a)θ=0 (b)θ=-0.12 rad (c)θ=-0.26 rad (d)θ=-0.362 rad图12 网格体积变化控制Fig.12 Variation control of mesh volume θ(rad)0-0.12-0.26-0.362dr (mm)12.21211.49810.64210.015 (1)特征网格的大小确定。通过对特征网格在不同方向按指定参数缩放,同时对边界参数化结果进行同比例的缩放,可实现特征网格在基网格上的局部方向缩放和全局缩放,图13a给出了一个圆形凸台在不同方向下进行缩放后的最终融合效果。 (2)特征网格的位置确定。即基网格上参数化区域中心点的确定(仅适用于特征网格边界对称的情况,此时认为边界参数化中心为边界几何中心)。考虑传统实体建模流程与零件对位置公差的严格要求,首先在基网格上选取几何参照,然后通过给定约束进行求解。圆形凸台分别在矩形平面上的任意定位和圆平面上的圆心定位见图13b和图13c。对于矩形平面,首先提取平面上相交两条边,并以此作为二维基底,通过指定距离参数即可确定平面内任意位置;对于圆平面,利用2.5.1节中方法确定圆心。对于特征网格边界非对称的情况,可以根据参数化中心与特征网格上某特定图元的位置关系和添加的约束间接求解。 (3)特征网格的旋转通过对二维参数域进行旋转来实现,旋转的角度需要通过两网格间的约束来确定。图13d给出了一个吊耳在平面中心点不同转向的情况。由于在距离权值分布优化后特征网格的保形性很高,故这里近似认为特征网格上的二维平面与基网格上的二维平面平行。二维平面分别由网格上的特征边来确定。定义X轴和X′轴的夹角为α,α分别取0°、45°、90°的情况见图13d。 对图2中拨叉零件利用本文方法进行整体融合建模并分析其精度,见图14。图14a是对图2a利用Creo 3.0设计的实体模型进行网格划分(步长0.5 mm)后的网格模型;图14b是利用本文方法在基网格Base上分别对三个特征网格Part1、Part2、Part3进行融合最终得到的重建结果;图14c是网格图14a与图14b的偏差映射图,在Geomagic Studio 2012中得到。图14c的局部放大图及偏差信息见图15,其中浅色部分正负偏差在0.04 mm之内,最大偏差为+0.213 mm和-0.253 mm,标准偏差0.017 mm。从图15中可以看出,只有在融合结合处偏差较大,在其他部分偏差很小,精度高。 (a)圆形凸台在不同方向下缩放后的融合效果 (b)圆形凸台在矩形平面上的定位 (c)圆形凸台在圆平面的圆心定位 (d)吊耳在平面中心点不同转向的情况图13 简单几何约束Fig.13 Simple geometric constraint (a) (b) (c)图14 建模流程及对比Fig.14 Modeling process and comparison 图15 局部偏差映射图Fig.15 Local deviation map 图14b中拔叉零件重建的算法耗时见表3。算法耗时主要与模型大小有关,但同时也与特征网格边界大小、形状,目标网格参数化面积等有关。根据设计流程将算法耗时分为边界参数化时间t1和局部参数化与特征网格重建时间t2。从耗时上来看,t1是t2的10倍左右,但是对特征网格来说,边界参数化只需要进行一次,在得到参数化结果后保存并与其他已参数化特征网格一起组成特征库。在新零件设计时对于需要的特征只需要从特征库中取出然后进行融合,此时执行目标网格局部参数化与特征网格变形重建部分,耗时在百毫秒级别,故在对特征网格进行缩放、旋转、移动位置等交互操作时也能实时重建。从特征库构建及重用设计流程上来看,对于已有的特征,不管其复杂度大小(如Part2一个简单类圆柱体,Part3一个几何结构较复杂的叉型结构),均能够通过网格融合来实现特征重用,且耗时相差不大;在实体建模中,要想实现较为复杂的特征重用是比较困难的,需要逆向数据提取与再设计,不仅专业要求较高,耗时还比较长。 表3 模型大小及算法耗时 (a)缩放Part1 (b)移动Part2 (c)缩放和移动Part3 (d)替换Part3 图16 变型设计及特征重用Fig.16 Variant design and feature reuse 对特征Part1、Part2、Part3进行重用,设计出结构不同的系列化拨叉零件,见图16。其中图16a改变了Part1的大小,图16b改变了Part2的位置,图16c改变了Part3的大小和位置,图16d则对Part3进行了替换,实现了另外一个特征的重用。可见该方法可以有效实现零件特征的重用,并且操作简单灵活,有效缩短新模型的建模时间。 (1)本文针对零件中设计重用困难的问题提出了网格融合技术,该技术简单方便,有效缩短了新模型的建模时间,提高了设计效率,并使重建结果具有良好的保形性,在一定精度范围内满足设计要求。 (2)本文方法可重用任意复杂的特征,同时对设计人员的专业水平要求较低,具有大众化的特点。 (3)增材制造技术在设计方面突破了传统设计思维的束缚,使得产品设计趋向个性化、艺术化,以上特点促使该方法在新模型的探索、创新设计上有着更为重要的意义;同时由于设计自由度较大,对于非专业设计人员可能出现设计模型无法满足力学性能等一些问题。 (4)本文方法对特征网格必须有一个边界环的要求使其在零件适用范围上存在一定局限性。 (5)对零件特征的定义需要进一步完善,对模型的特征分割理论及组合表达有待进一步研究。 (6)存在融合边界处形变较大造成的应力集中问题,可以考虑局部光顺操作。

2.4 特征网格体积膨胀收缩优化
2.5 特征图元提取与几何约束
3 实验分析
3.1 基于层的网格变形优化结果
3.2 体积膨胀收缩优化结果
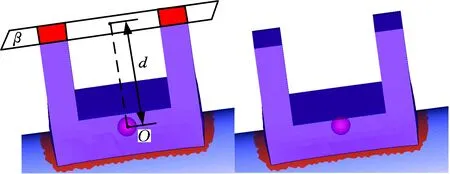


3.3 几何约束结果
3.4 零件整体建模及精度分析
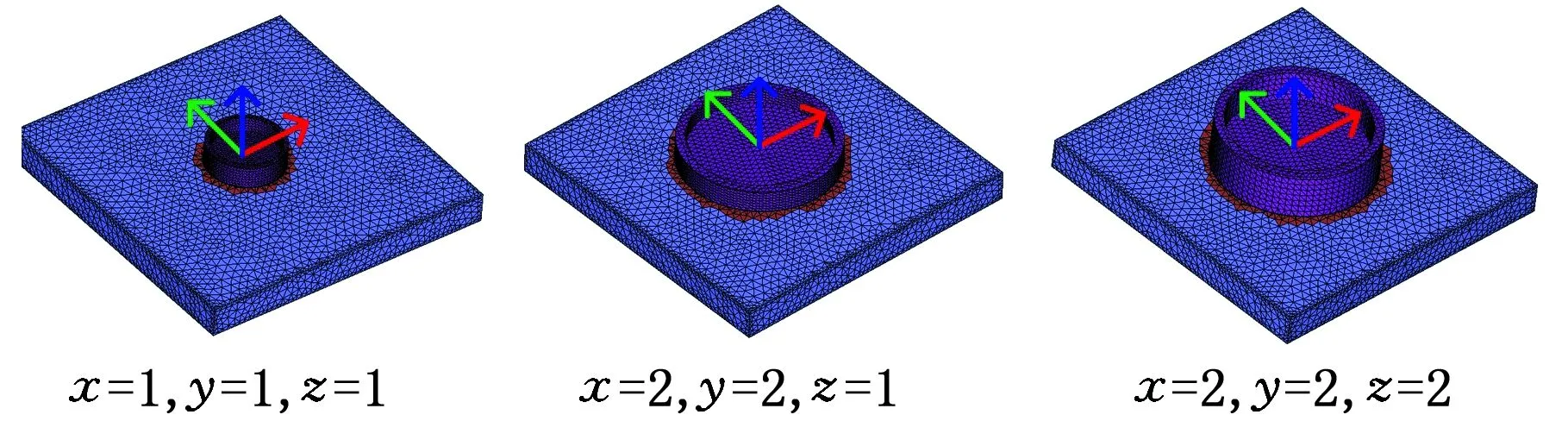
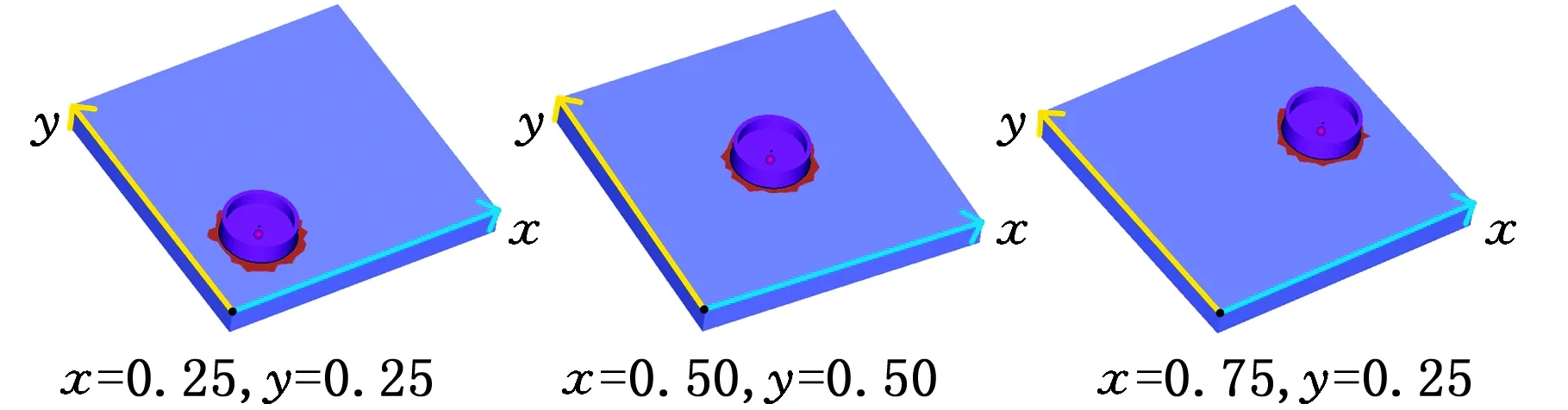
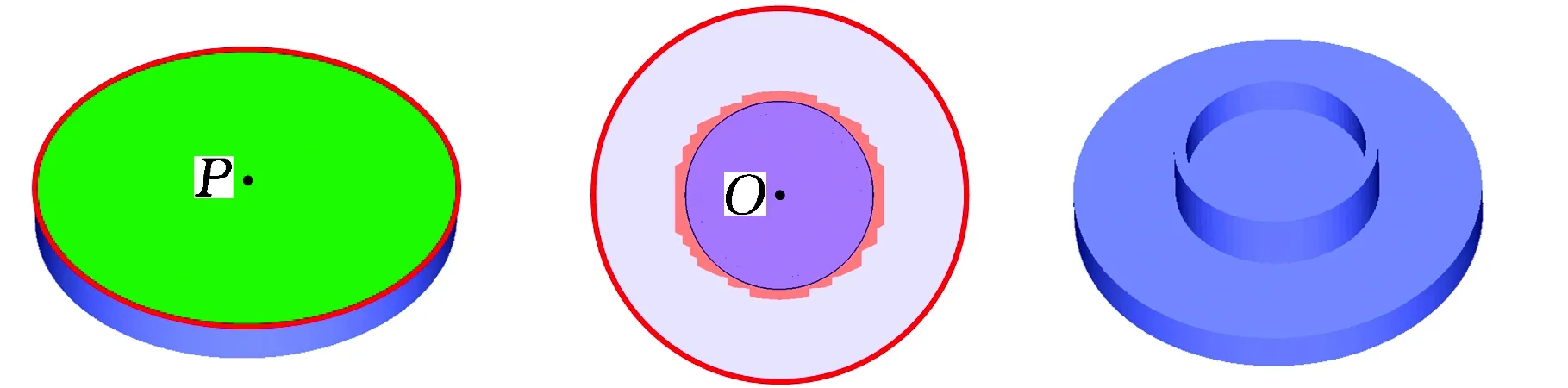
3.5 算法效率与特征重用实现

4 结论
