椭球面的傅立叶限制性问题
2018-12-19范美玲
范美玲
(汕头大学理学院,广东 汕头 515063)
0 引言
傅立叶限制性问题的研究一直是调和分析中的热点之一.1967年,E.M.Stein提出对于给定的Lp可积函数f,限制f的傅立叶变换ˆ到n-1维球面S上,则(A<CB,其中C为常数,在此简记为,A≾B)成立当且仅当,这个问题后来被称之为限制性问题.Fefferman和Stein[1]证明了在n=2时除端点之外的所有情况成立,Zygmund[2]在1974年给出了端点处的证明.Cordoba[3]在1977年用不同的方法证明二维的情形是成立的.对于高维情形,虽然已经得到了很多丰富的结果,但到目前为止它仍然未被解决,其中一个较好的结果是由Tomas和Stein[4]给出的,他们证明了当 q=2 且成立.但是他们的证明充分利用L2空间的性质,对于一般的q,该方法不能推广,而这也是限制性问题困难所在.众所周知,傅立叶限制性问题,Kakeya极大函数问题和Bochner-Riesz求和问题等都是相互关联的,著名数学家Wolff,Bourgain,Fefferman,Tao等在这些问题的研究上取得了一系列进展(见文献[5]),与其相关的方法和技巧已经广泛应用于PDE,谱理论,数论等.本文是在他们研究的基础上进一步拓广傅立叶限制性问题的内容,我们限制f的傅立叶变换在椭球面上,给出椭球面上限制性问题对应的指标p,q所必须满足的条件,并证明二维是成立的.
1 定理的提出
1.1 预备知识
首先我们回顾经典球面上的限制性猜测,它具体描述如下:
针对该问题,一个非常自然的想法是将球面换成椭球面,相关的结论是否还成立,这也是本文的出发点.为方便叙述,本文均假定E为下面形式的椭球面,,相对应的面测度为dσ.那么本文的主要结论如1.2.
1.2 主要结论
在该定理的基础上,一个非常自然的想法是反过来是否成立,即下面的猜测.
猜测(椭球面的傅立叶限制性猜测)
它和球面限制性问题一样,对于高维情形,困难依然存在,但是我们可以给出二维的证明,这也是本文的第二个主要结论.
定理2(二维的椭球面限制性定理)
2 定理1的证明
为证明定理1,先给下面的引理.
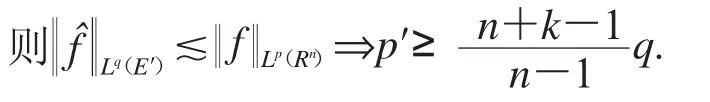
证明:证明思路是构造函数f,使f的傅立叶变换集中在E′附近.
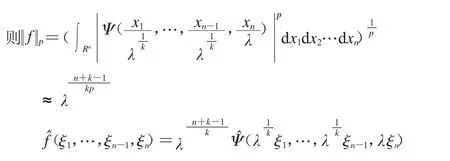
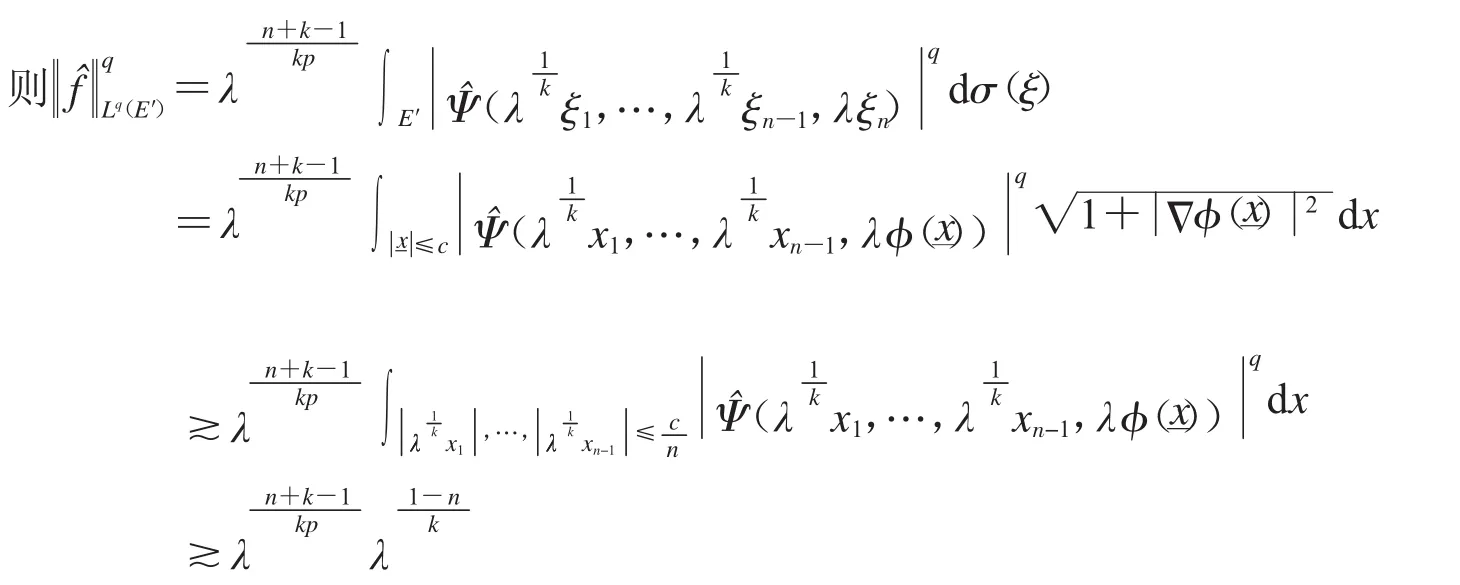
这样就完成了引理1的证明.
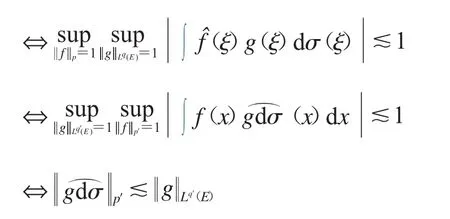
定义1:φ 是实值的 C∞(Rn)函数,a(x)是函数,定义是参数.
引理2[6]若 Ω⊂Rn是开集,φ(x):Ω→R 是 C∞函数,p∈Ω 且 φ(p)≠0,a(x)支撑在p的一个小邻域内,则对任意N,
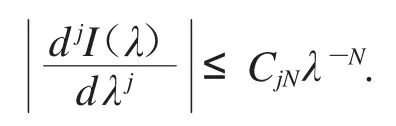
引理3[6]若Ω⊂Rn是开集,φ(x):Ω→R是C∞函数,在p点的Hessian矩阵H(φP)可逆,令σ是H(φP)的正负符号差,且a(x)支撑在p的一个小邻域内,,则对于任意N,
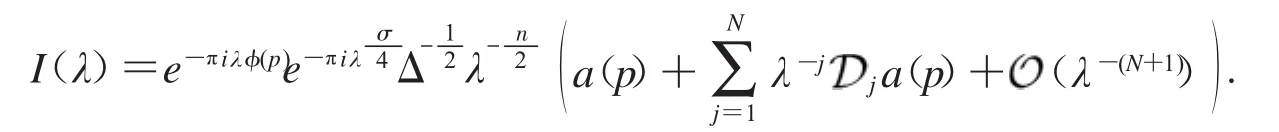


这样就完成了定理1的证明.
3 定理2的证明
要证明定理2,我们需要下面的引理4.
引理4[8]分割圆S的弧间距和θ相互控制,若f和g支撑在S的不同θ弧上,则
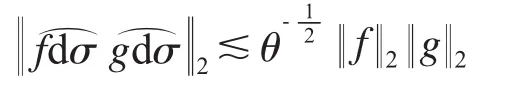
首先,要证定理2成立,我们只需证明其对偶形式成立.即证明⇔p′>4 且 p′≥3q.
事实上,我们可以进一步简化指标,即在条件p′=3q>4下成立即可.
首先注意到
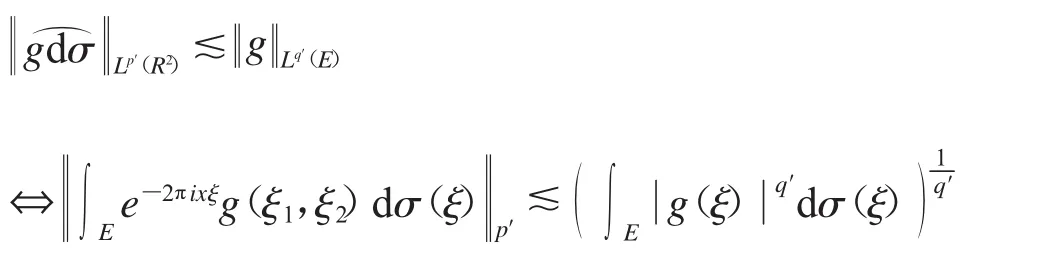
我们先把在椭圆上的积分转化到圆上,详细过程见式(1).
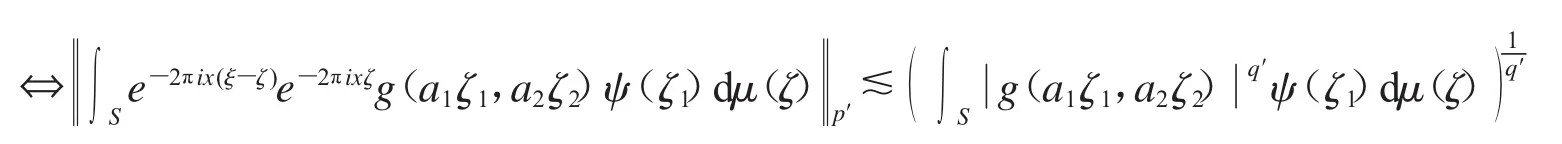
我们用Whitney分解方法[9]处理上述估计式,把圆周S平均分成2n等份,平分后所有圆弧的集合记作An.那么对任意n≥0,在n阶段分割后所得的任意圆弧在n+1阶段都有两个子体.定义I~J:I,J不相邻,I,J∈An,但存在n,使得他们的母体相邻.那么它具有下面的性质:∀x≠y,∃,I~J,s.t x∈I,y∈J.从而,
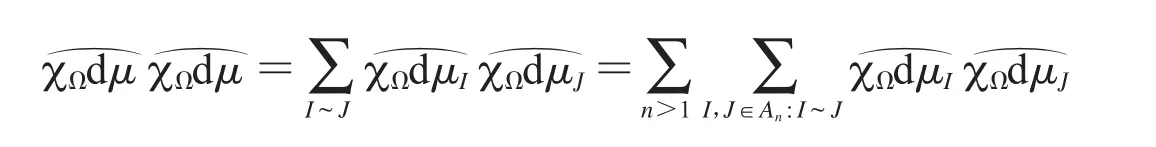
其中dμI=χ(Ix)dμ(x),dμJ=χ(Jx)dμ(x).故有