CT系统参数标定及成像
2018-12-19谢睿诚刘楚欣潘玉媚
谢睿诚,刘楚欣,潘玉媚,李 健
(汕头大学理学院数学系,广东 汕头 515063)
0 引言
CT,即计算机断层成像技术,是一种依据外部投影数据重建物体内部结构图像的无损检测技术.CT系统示意图见图1.
王召巴[1]在2001年从滤波反投影算法的基本原理着手,分析了CT系统旋转中心偏移对图像重构所造成的影响;Olander等[2]利用Radon变换性质把角度相差180°的投影经过平移与翻转,计算出旋转中心的偏移量;李增云等[3]再次证明了物体质心与其投影质心关系定理,并提出了利用部分投影快速校正CT系统旋转中心的方法.这些方法理论上可以准确地确定CT系统旋转中心的位置再进一步进行图像的重构,但现实中往往因为其计算复杂,实操性不强等原因而难以在医学和工业方面被广泛应用.
由于CT系统对系统旋转中心在托盘中的位置、探测器单元之间的距离以及X射线的180个方向等参数有极高的要求,这极大地增加了CT系统制造和安装的难度.本文运用滤波反投影和Radon变换等,针对CT系统参数标定及成像展开研究.
1)建立了直接求解模型,求解CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向,然后利用重构法验证其结果.
2)建立滤波反投影模型计算未知介质的衰减系数,然后通过Radon变换和Beer-Lambert定律导出吸收率的计算公式,并由此计算未知介质吸收率.并根据此前确定的标定参数对吸收率数据进行校正,得出指定位置的吸收率,并重构出未知介质的图像.
3)定义模板标定参数与实际参数的误差为精度度量指标,定义重构前后吸收率的变化为稳定性度量指标.然后以矩形和正方形代替椭圆和圆建立新的标定模板,减少滤波反投影中插值方法产生的误差.最后,通过对比两个模板重构前后吸收率差距和重构前后吸收率变化量,认为方形模板的精度和稳定性比椭圆形模板更好.
本文的原文获得2017年全国大学生数学建模竞赛一等奖,所采用的数据亦来自2017年全国大学生数学建模竞赛(http://www.mcm.edu.cn/html_cn/node/460baf68ab0ed0e1e 557a0c79b1c4648.html).
1 问题提出
1.1 问题提出
问题1:在正方形托盘上放置两个均匀固体介质组成的标定模板,模板的几何信息如图2所示,其中每一点的数值反映了该点的吸收强度,这里称为“吸收率”.根据这一模板及其接收信息,确定CT系统旋转中心在正方形托盘中的位置,探测器单元之间的距离以及该CT系统使用的X射线的180个方向.
问题2:附件3是利用上述CT系统得到的某未知介质的接收信息.利用问题1中得到的标定参数,确定该未知介质在正方形托盘中的位置,几何形状和吸收率等信息.另外,请具体给出图3所给的10个位置处的吸收率.
问题3:附件5是利用上述CT系统得到的另一个未知介质的接收信息.利用问题1中得到的标定参数,给出该未知介质的相关信息.另外,请具体给出图3所给的10个位置处的吸收率.
问题4:分析问题1中参数标定的精度和稳定性.在此基础上自行设计新模板,建立对应的标定模型,以改进标定精度和稳定性.

图1 CT系统示意图

图2 模板示意图(mm)
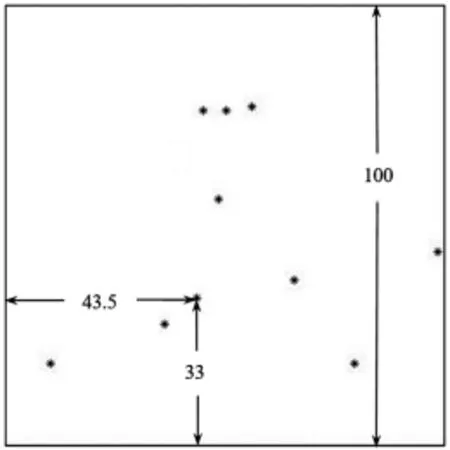
图3 10个位置示意图
2 CT图像重构模型推导
2.1 Radon变换和吸收率
根据文献[4],附件3中的接受信息数据即Radon变换的投影函数值,问题2、3是要求根据投影函数值来求吸收率,我们以衰减系数为桥梁构建投影函数值与吸收率之间的关系.Radon变换示意图见图4.

图4 Radon变换示意图
2.1.1 Radon变换(投影函数值与衰减系数的关系)
设p轴与X射线垂直,p=xcosφ+ysinφ.设未知介质的函数为f(x,y),未知介质经X射线投影在p轴上得到,即:

上述是Radon变换的原理,但在这个问题中,我们已知的数据是附件3中的接收信息数据即Radon变换的投影函数值,要通过来求 f(x,y)的函数值,得出物质的吸收率来画出物质的图像,因此本问题可以转换为求Radon变换的逆过程,根据文献[4],这个过程就是图像重构的过程,我们将采取滤波反投影的方法来得到f(x,y).
2.1.2 Beer-Lambert定律(衰减系数转换为吸收率)
由Beer-Lambert定律[8]可知:
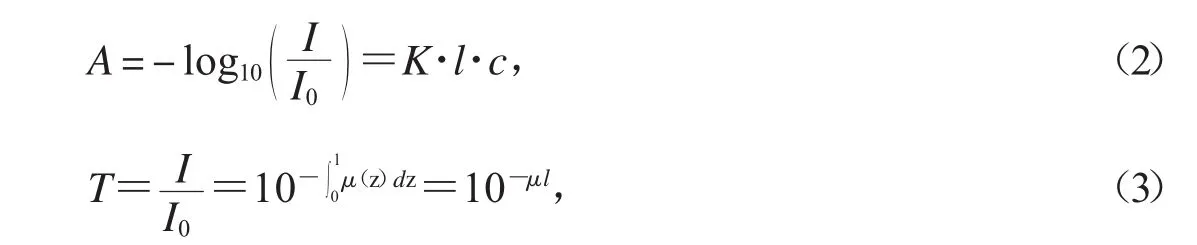
其中,A为物体的吸光率,K为吸收率(对于某种均匀的物质,K为常数),l为介质厚度,c为吸光物质浓度(对均匀物体,c为常数).
设μ为衰减系数,令

即衰减系数和吸收率之间的关系是线性关系.
据公式(1)和公式(4)有:
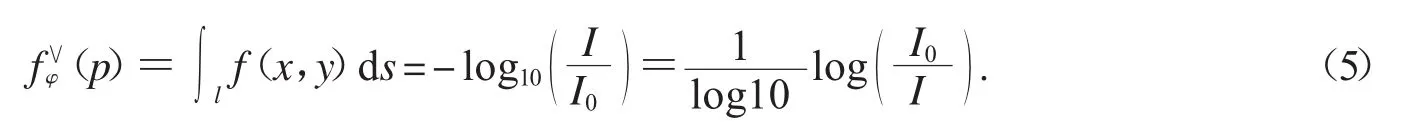
因此可以根据物体在不同角度下X射线的接收信息利用滤波反投影原理来重构物体.
2.2 滤波反投影原理
2.2.1 投影切片定律:

F(ωcosφ,ωsinφ)见 2.1和 2.2.2中说明.
2.2.2 二维傅里叶变换及极坐标变换:
定义

为f(x,y)的二维傅里叶变换.
令 u=ωcosφ,v=ωsinφ,则有函数
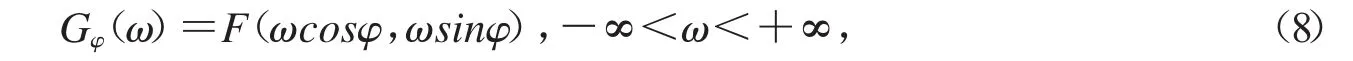
式中G(φω)为通过φ角的F切片,对固定的φ,G(φω)只有一个自变量.

那么上式可以表示为:

2.2.3 滤波器(文献[5]):
根据傅里叶变换的卷积定理:
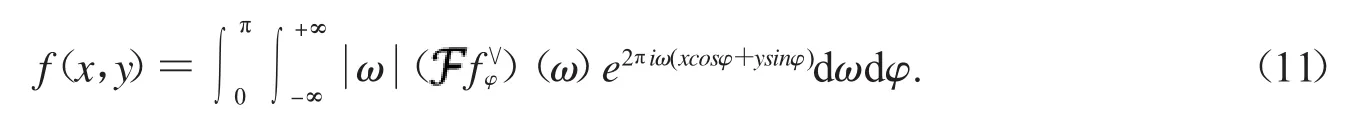

2.2.4 傅里叶逆变换
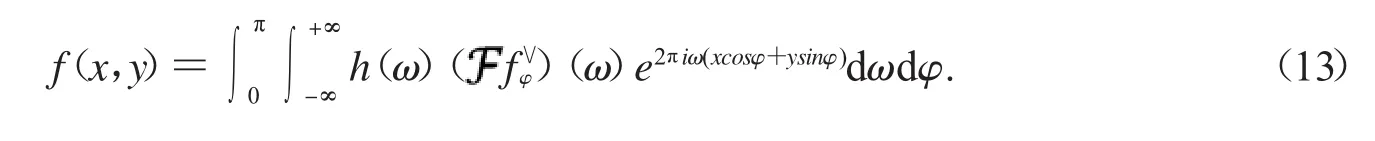
但我们运用上式的离散化形式:
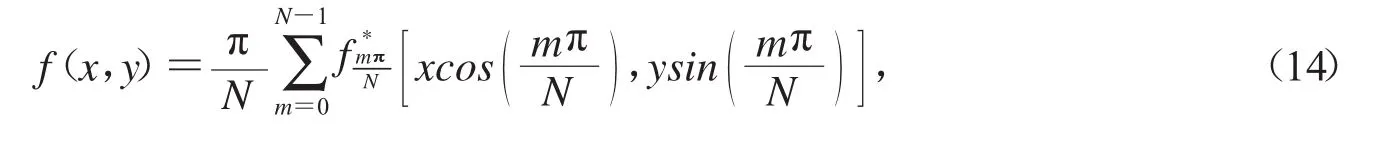
2.3 滤波反投影原理在本题中的应用
滤波反重构原理要应用于本题重构过程中,还需要解决下面两个问题:插值方法的选择和滤波器的选择.
2.3.1 插值方法的选择
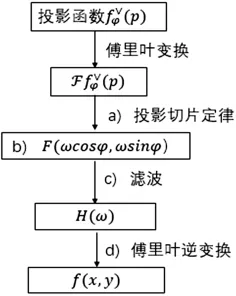
图5 滤波反投影步骤图
a)线性插值
线性插值中插值点xi,i=1,2,…,511对应的投影函数的计算公式如下所示:
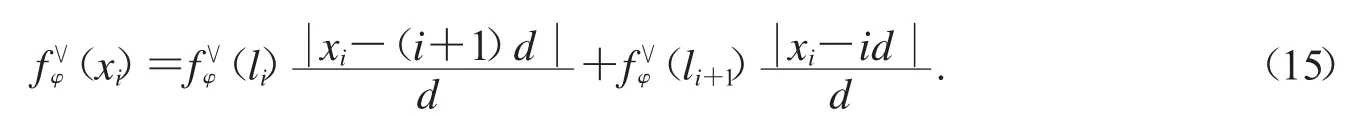
b)三次样条插值
三次样条插值法中插值点 xi,i=1,2,…,511对应的投影函数的计算公式如下所示:
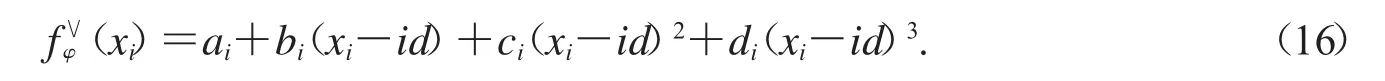
其中ai,bi,ci,di为参数,由确定.
2.3.2 滤波器的选择
我们选择的滤波器是Cosine滤波器,Cosine滤波器是在Ram-Lak滤波器的基础上乘上一个Cosine函数.
Ram-Lak滤波器:
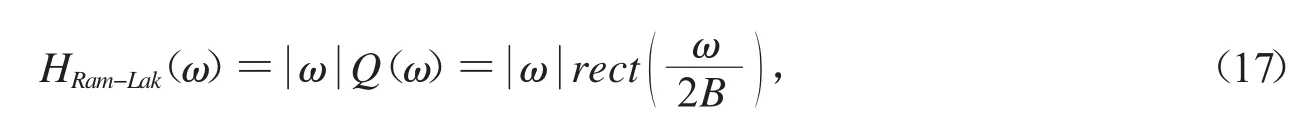

3 问题1模型的建立与求解
3.1 确定探测器单元之间的距离d
探测器单元之间的距离d,可理解为探测器单元数密度的倒数,即该问题可通过求解探测器单元数密度来解决.
a)根据附件提供的第151次旋转数据,光源平行于y轴时,接收到信息的探测器单元个数n为108个.结合模板的几何信息可知,108个探测器单元个数对应的实际距离l为30 mm,即探测器单元数密度ρ为:
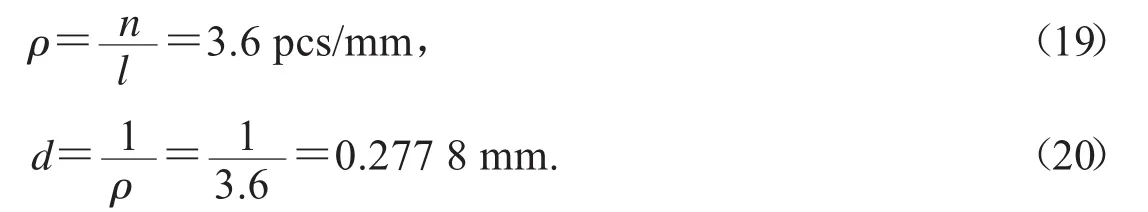
b)根据附件中第61次旋转的数据,光源平行于x轴时,接收到信息的探测器单位个数为288个.图2模板示意图提供的长轴长度为80 mm,类似地,根据a)可求出探测器单位数密度同样为3.6个/mm,探测器单元之间的距离d为0.277 8 mm.
经以上分析可得探测器单元之间的距离为0.277 8 mm.
3.2 确定CT系统使用的X射线的180个方向
利用重构原理(详见2.1 Radon变换和吸收率),将附件2数据进行重构图像,得到的重构图像如图6所示:
观察图6发现,附件2数据重构图像发生了明显的角度偏转.利用椭圆与圆圆心连线与水平方向的夹角即重构所得图像的偏转角度为29.649 3°.因此,扫描光源初始方向为与x轴负半轴夹角为60.350 7°,从第四象限指向第二象限的方向,扫描光源最终方向为初始方向的逆方向,每次CT系统逆时针旋转1°.
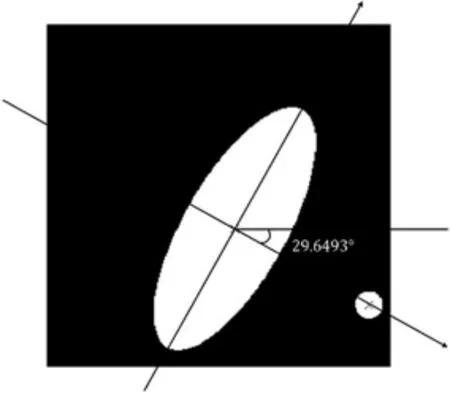
图6 附件2数据重构得到的图像
3.3 求解CT系统旋转中心
利用3.2中得到的初始旋转角度,对重构图像进行修正结果如图7所示.
由于椭圆模板在标定时放置在托盘的正中央,其重构图像也应该在正中央,可是图像中椭圆形的中心与图像中心并不重合,因而可以利用椭圆中心与图像中心的偏差来确定CT系统的旋转中心.
以重构图像的椭圆圆心为原点,建立图8所示坐标系,图像中心位于直角坐标坐标系的第二象限,求得图像中心的位置为(-8.998 5,5.999 1).
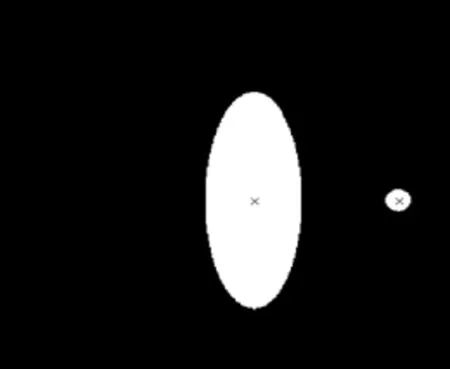
图7 调整角度后重构得到的图像
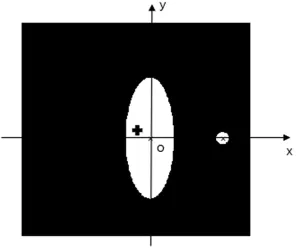
图8 置于坐标系的重构图像
4 问题2,3模型的建立与求解
4.1 吸收率校正模型
利用滤波反投影原理对标定模板的180个角度的接收信息进行重构,并利用3.2和3.3中所得角度和旋转中心位置,对重构图像的方向和位置进行校正.可得图像标定模板中吸收率为1.000 0处的衰减系数的观测值中位数为0.490 4,标定模板中吸收率为0.000 0处的吸收率中位数为0.000 1.由Beer-Lambert定律,可以得吸收率与衰减系数关系为:

4.2 问题2图像重构
依据2中建立的模型,利用滤波反投影原理对附件3所给的接收信息进行重构,并利用公式(21)进行校正,得到重构图像如图9所示,问题中指定的10个位置处的吸收率结果如表1所示.
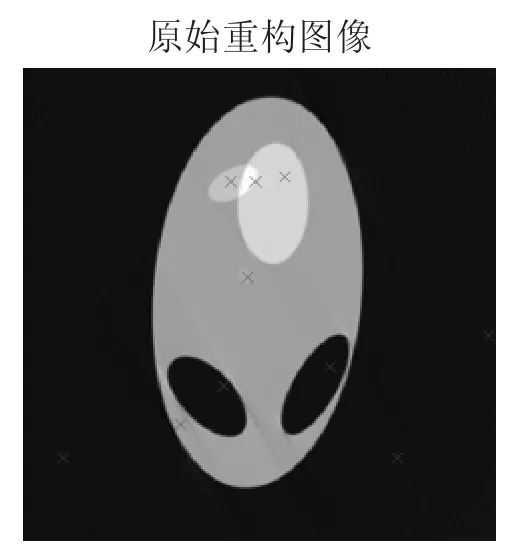
图9 原始重构图像(标记指定位置)
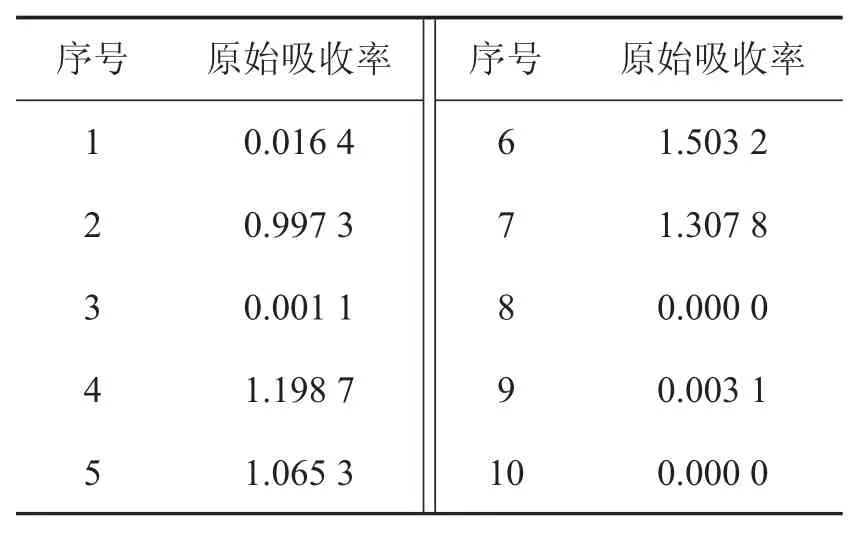
表1 图9所给10个位置处的吸收率结果
4.3 问题3图像重构
利用2中建立的模型,根据滤波反投影模型将CT系统得到的未知介质接收信息,即附件5数据进行图像重构,并利用公式(21)进行优化,得到的重构图像如图10所示,问题指定的10个位置处的吸收率结果如表2所示.
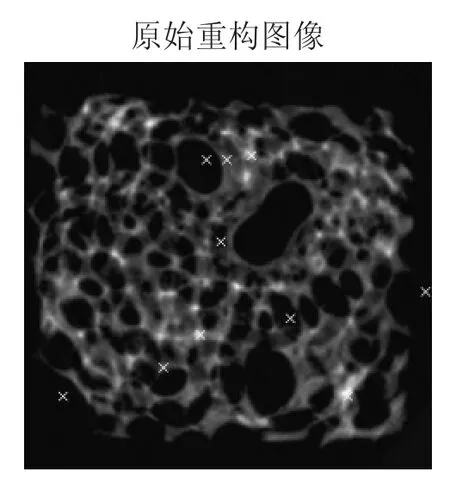
图10 原始重构图像(标记指定位置)
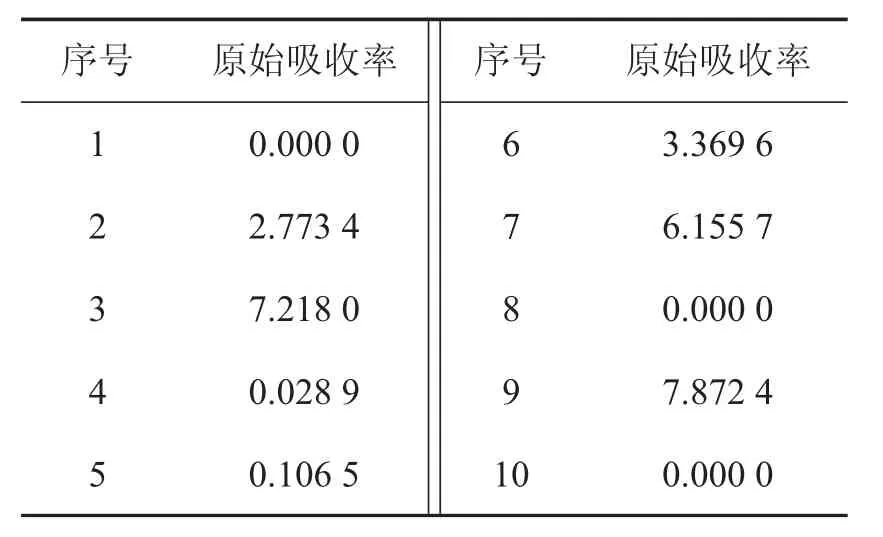
表2 图3所给10个位置处的吸收率结果
5 问题4模型的建立与求解
5.1 模型的建立
5.1.1 精度评价
1)模板位置对校正精度的影响
通过平移,旋转变换,改变模板的位置并对模板做Radon变换,得到模板的接收信息,并利用3中确定旋转中心和初始投影角度的方法,求解旋转中心和初始投影角度.与实际位置进行比较,重复多次并求平均值,得到平均误差作为精度估计依据.
2)Radon变换再重构的吸收率差距
对模板作Radon变换得出模板的投影数据,再用投影数据运用2中建立的重构方法还原图像,在模板和重构得到的图像中建立相同的坐标系,比较相同坐标下两者的吸收率数值差距,设前者为fo(x,y),后者为fl(x,y).
用L2范数来衡量fo(x,y)和fl(x,y)之间的差距R,设已知吸收率的点构成m×m的矩阵:
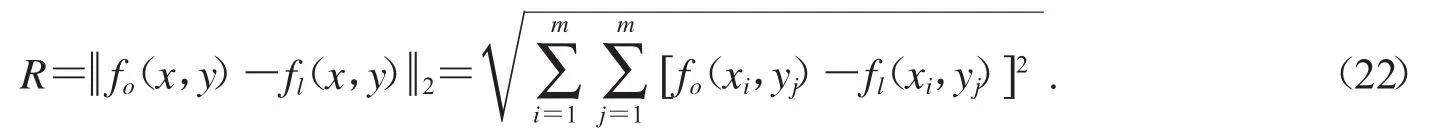
用均方误差来衡量吸收率的差距大小,均方误差计算公式为:
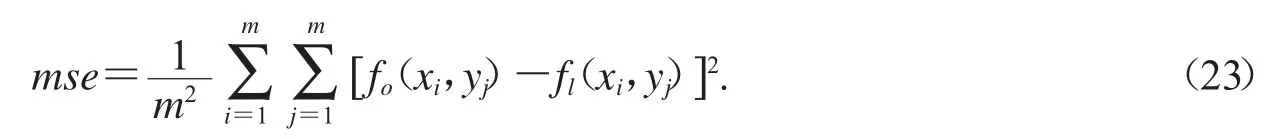
5.1.2 稳定性评价
我们用各参数对精度的影响来衡量模板的稳定性,在两种模板的精度足够好的情况下,通过改变反投影方向数、旋转中心平移距离、初始旋转角度大小以及计算精度指标中的重构前后吸收率差距的变化量来说明其稳定性,即吸收率差距变化不大就认为模板的参数标定精度稳定,反之则不稳定.
5.2 新标定模板设计
5.2.1 原始标定模板误差成因分析
a)角度变化引起的探测器数目变化量
附件2中被判断为X射线扫描光源方向平行于x轴的数据有7组,即第58次扫描至第64次扫描得到的接收信息的探测器单元个数相同.考虑造成这样现象的原因是当X射线扫描光源方向旋转至与x轴夹角较小的区域内时,每逆时针旋转一次引起标定模板投影的接收数据变化量极小,且CT系统测量的精度不高,不足以反映出如此微小的变化量.
b)插值方法的适应性
由于重构方法中应用的是线性插值方法,椭圆的边缘为圆弧状,线性插值并不能完全贴合椭圆边缘,在线性插值中会引起误差.即使用其它插值方法如多项式插值方法也不可以完全贴合,因此原始模板会在重构图形时产生误差.
5.2.2 新模板设计
针对原始模板的不足之处,我们构建新的模板(方形模板)如图11所示:

图11 新模板示意图
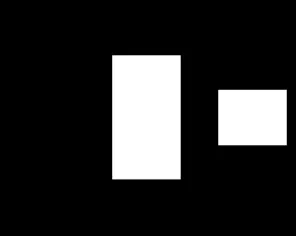
图12 新模板吸收率
如图11所示,新模板(方形模板)由矩形和正方形组成,矩形中心在正方形托盘的中心,矩形和正方形均关于正方形托盘的水平对称轴对称,其几何信息如图11所示.
5.3 模板测试
我们对椭圆模板(原始模板)以及方形模板(新模板)做Radon变换以及重构,并进行精度分析和稳定性分析.
5.3.1 精确度评价对比
对椭圆模板和方形模板做20次不同的平移变换和30次不同角度的旋转变化,并计算坐标和旋转角度与实际值的平均误差(见表3).

表3 椭圆模板和方形模板的校正精度对比
从表3可以看出,椭圆模板和方形模板的标定参数的误差都比较小,精度较高,因而两个模板都适合参数标定.
5.3.2 稳定性评价对比
由于CT系统是以等角度间隔扫描一次方式离散进行的,我们定义CT系统扫描1周所做投影的数量,也即重构图像时可以利用的轮廓数量为反投影方向数.为探究在反投影方向数减少,投影方向的角度间隔增大时,两种模板的稳定性.以反投影方向数为横坐标,以模板原吸收率与重构后模板吸收率的欧几里得距离和均方误差为纵坐标,建立平面直角坐标以呈现椭圆模板和方形模板在吸收率差距这一精确度指标上的差别.
由图13和图14可以看出,在反投影方向数范围为(0,180]时,方形模板与椭圆模板相比,重构前后吸收率差距都比较小,并且在减少反投影方向数时,方形模板吸收率差距的变化量比椭圆模板的要小,这说明方形模板的稳定性比椭圆模板的要高.
进一步探究模板摆放时旋转中心位置及旋转角度对精度的影响,分别以旋转中心平移距离和旋转角度为横坐标,以模板原吸收率与重构后模板吸收率的欧氏距离为纵坐标,建立平面直角坐标系得到图15,图16(平移距离)以及图17图18(旋转坐标),椭圆模板和方形模板在稳定性指标上的差别见图15-图18.
由图15图16可以看出,在调节旋转中心的位置变化时,椭圆模板的误差要稍小于方形模板,并且二者的误差都很小(mse<0.001),很难区分方形模板与椭圆模板的精度和稳定性差距.进一步的,从旋转角度变化的影响来探究(见图17图18)椭圆模板和方形模板的差距.
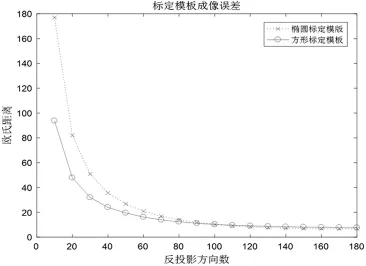
图13 不同反投影方向数下两种模板重构前后吸收率差距对比(以欧几里得距离衡量)
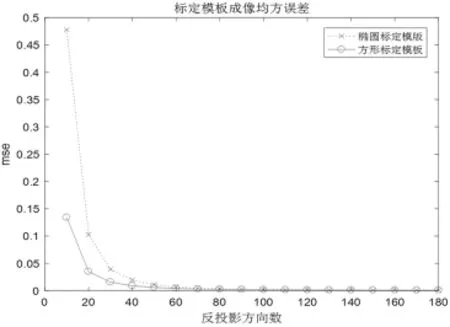
图14 不同反投影方向数下两种模板重构前后吸收率差距对比(以均方误差衡量)
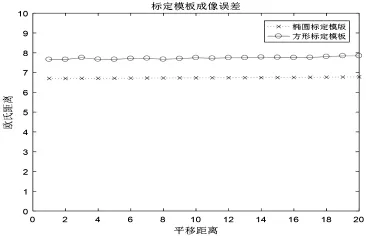
图15 不同平移距离下两种模板重构前后吸收率差距对比(以欧几里得距离衡量)
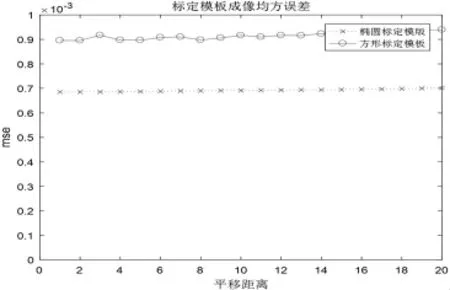
图16 不同平移距离下两种模板重构前后吸收率差距对比(以均方误差衡量)
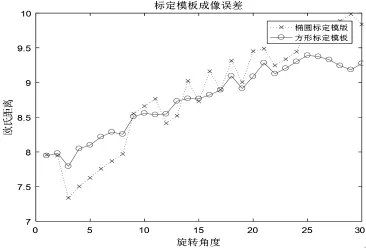
图17 不同旋转角度下两种模板重构前后吸收率差距对比(以欧几里得距离衡量)
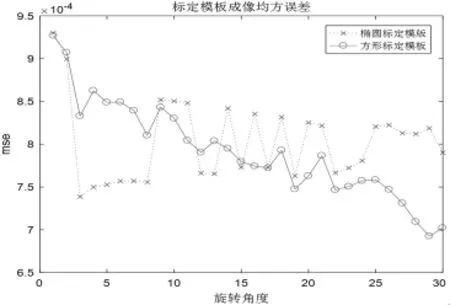
图18 不同旋转角度下两种模板重构前后吸收率差距对比(以均方误差衡量)
由图17和图18可以看出,在改变旋转角度(横坐标)时,在旋转角度大于10°时,方形模板重构前后的吸收率差距比椭圆模板的小,并且在旋转角度小于10°时,二者误差都很小,因而认为模板的摆放角度对标定精度影响不大.
综上所述,改变反投影方向数时,方形模板的稳定性优于椭圆模板;平移,旋转时方形模板和椭圆模板重构的误差都极小.故使用方形模板作为标定模板要优于椭圆模板.
6 模型评价
本文建立的滤波反投影模型实现简单,精度高,运算量小,能获得较好的重建图像,对实际生产中的CT系统参数的修正有一定的帮助,但重构所得图像边缘出现伪影,虽然我们使用的中值滤波有效平滑去除图像的噪声点,但未能完全消除其影响,这也是后续深入研究的一个方向.
