潜艇垂直面波浪力计算与运动仿真*

陆斌杰，李文魁，周 岗，陈永冰

（海军工程大学电气工程学院，武汉 430033）

0 引言

潜艇运动为强非线性、强耦合的复杂运动。潜艇近水面航行时，由于受到波浪干扰力，其摇荡运动尤为复杂，对潜艇操纵造成极大影响，研究潜艇波浪中的运动规律对于潜艇操纵控制系统设计极为重要。理论上研究波浪力的方法主要有两类，一是按波浪力的量阶分成一阶（线性分量）和二阶波浪力（非线性分量）两部分；二是研究潜艇在波浪环境下的整体受力。第一种方法清晰反映波浪不同成分对潜艇的影响，物理意义明确，被广泛使用，其中主要有切片法、STF（scattering transfer function）法、三维面元法、细长体方法、Hirom近似法等。

文献[1]较早提出了切片概念，文献[2]提出了船舶纵摇切片理论，文献[3]提出了新的切片理论，可计入前部断面对后部断面流体动力的影响。文献[4]运用切片理论进行了潜艇二阶波浪力的计算。文献[5-7]采用STF流体动力切片理论[8]和 Frank源分布紧密拟合方法[9-10]计算各种复杂剖面和任意潜深的潜艇剖面水动力系数和波浪力系数，求解波频运动响应。文献[11-12]较早提出了基于势流理论的面元法和奇点分布法，计算一阶和二阶波浪力。文献[13-14]采用三维面元频域法计算了二阶波浪力。文献[9]提出细长体方法[14]结合 Newman[15-16]三维修正处理法计算二阶波浪力。为简化计算，文献[17]提出了Hirom近似公式计算波浪力。

上述文献中有关Hirom公式的研究和应用多集中于潜艇的线性运动模型，并以此对Hirom公式进行拟合，从而模拟出一个线性海浪模型，应用范围受限。且各文献对于公式的形式描述不一，因此，本文针对潜艇空间运动模型，对大量文献进行研究对比后，总结出准确合理的Hirom公式，并以此计算垂直面波浪力，并分别考察不同波浪条件、航行运动状态对潜艇近水面潜浮运动的影响。

1 潜艇近水面运动建模

1.1 潜艇运动坐标系

坐标系、名词术语、符号规则均采用ITTC和SNAME术语公报的体系[18-19]。固定坐标系（定系）E-ξηζ和运动坐标系（动系）O-xyz，如图 1所示。图1（a）为水平面坐标系，U 为潜艇航速，μ、χ分别为绝对浪向角和相对浪向角（遭遇角）。图1（b）为垂直面坐标系。

图1 坐标系

潜艇在不同坐标系下的运动变量如表1所示。

1.2 海浪建模

海浪扰动为复杂的随机过程。潜艇在长波作用下，其垂直位置受影响较大，而短波引起的垂向升沉力和纵摇力矩较小，因此，只考虑长峰波的情况[20]。对于充分发展、具有平稳随机性及各态遍历性的长峰波海浪，采用第12届ITTC推荐的Pierson-Moskowits波谱[20]，其谱密度为：

表1 潜艇在不同坐标系下的运动变量

采用波浪叠加法模拟海浪。频谱区间范围为谱峰频率的3倍～4倍。用等间隔法对波谱离散化。各级海况下的仿真频段和频率增量选取方法如下。

表2 各类海况下的仿真频段和频率增量的选取

海浪幅值响应为：

图2 ITTC单参数谱

1.3 波浪力计算

波浪力分解为一阶波浪力和二阶波浪力，前者使潜艇作波频摇荡，后者使潜艇作低频慢变、非线性的侧倾与漂移运动。

图3 海浪幅值响应（χ=180°、H1/3=3 m）

1.3.1 一阶垂荡力和纵摇力矩

一阶波浪力对潜艇的纵摇、垂荡均有很大影响。一阶波浪力幅值与频谱中各谐波波幅成正比，相位落后于各谐波。由流体力学理论知，距水面深度z处的次波面方程为：

式中，k为波数；ξ为位置；t为时间。水深ζ处的水压力为：

式中，P0为自由水表面的大气压力；ρg|ζ|为深度 ζ处的静水压力；ρgα|ζ|为次波面的波动压力；ρ为海水密度；g为重力加速度。

由流体力学和线性叠加原理，潜艇垂向运动所受的一阶垂荡力Z1和纵摇力矩M1计算式为[15-17]：

1.3.2 二阶垂荡力和纵摇力矩

二阶垂荡波浪力为指向水面、使潜艇抛向水面的定常力，其幅值正比于波幅平方，相对一阶力为较小量，且随水深减小呈指数增长。二阶垂荡力Z2和纵摇力矩M2计算式为[19-20]：

式中，CZ2=0.1、CM2=0.01为无因次水动力系数。

综合一阶和二阶浪力，纵向运动所受波浪力（矩）为：

1.4 波浪干扰下的潜艇操纵运动方程

波浪干扰下的潜艇运动方程由静水中的操纵运动方程叠加波浪力得到。静水运动方程采用潜艇标准运动方程简化得到的空间操纵运动方程[20]。

垂向方程：

纵倾方程：

式中，h为稳心高。

运动方程：

式中，mg 为艇重，h 为稳心高，δb、δs分别为艏舵角和艉舵角，φ为横摇角。

2 模拟仿真

选取文献[21]中的潜艇参数，进行潜艇近水面航行时垂直面运动仿真。分别分析初始潜深、航速、初始浪向角、有义波高对潜艇非线性潜浮运动的影响。除单独说明外，默认仿真条件为：有义波高3 m、顶浪（χ=180°）、航速 5 kn、初始潜深 15 m。

1）不同初始潜深航行的深度、纵倾响应见图4。初始潜深越浅，上浮越快，纵倾角越大；当初始潜深大于35 m，潜艇上浮不明显，纵倾角小于0.5°，可稳定直航。图5为默认仿真条件下的所受波浪力情况。波浪力量级大于波浪力矩，一阶波浪力量级大于二阶波浪力，二阶波浪力方向恒定，并指向水面。

2）不同航速下的深度、纵倾响应见图6。较低航速时潜艇易上浮，且纵倾角越大；当航速超过一定值，航速越大，潜艇越不易上浮，纵倾角越小。

3）不同初始浪向角下的深度、纵倾响应见图7。潜艇各浪向下航行受影响程度排序为：顶狼＞顺浪＞艉斜浪＞艏斜浪＞横浪。顶浪航行最易上浮，纵倾角最大；横浪航行最难上浮，纵倾角最小。

4）不同有义波高下的深度、纵倾响应见图8。有义波高越大，越易上浮，纵倾角越大。

图4 不同初始潜深下的深度、纵倾响应（Hs=3m，χ=180°，u=5kn）

图5 潜艇所受波浪力（Hs=3 m，χ=180°，u=5 kn）

3 结论

图6 不同航速下的深度、纵倾响应（Hs=3 m，χ=180°，ζ0=15 m）

图7 不同遭遇角下的深度、纵倾响应（Hs=3m，，u=5kn，ζ0=15m）

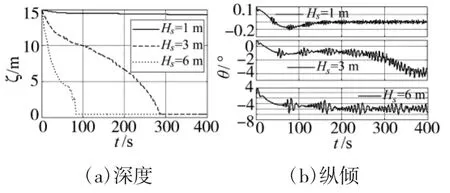
图8 不同有义波高下的深度、纵倾响应（χ=180°，u=5kn，ζ0=15m）

本文采用Hirom近似公式计算垂直面的波浪力，仿真表明，在一阶波频波浪力和二阶波浪力共同作用下，潜艇近水面低速航行时产生上浮现象，且潜深越浅、浪级越高、航速越低，潜艇越易上浮，顶浪航行最易上浮；单独操艏舵或艉舵，产生的舵力无法克服二阶波吸力，潜艇依旧上浮。低速近水面航行时，顶浪航行纵倾角最大，横浪航行纵倾角最小。结合文献[8-9，13-14]的研究结果，本文提供的Hirom近似公式和计算方法合理有效，可用于潜艇运动模拟仿真。