公路桥梁车辆荷载与疲劳寿命的技术研究

魏德林

(中铁十八局集团第一工程有限公司,广东 清远 511510)

全球都在积极研究桥梁疲劳问题。比如：英美国家系统规范了桥梁荷载,包括各种器件的疲劳程度、疲劳荷载等级设计、疲劳车辆模型等内容。国际对车辆疲劳荷载计算的方式包括：一种是关于荷载分布规律,具体根据交通产生的大量数据,整体分析典型车辆荷重以及对应频率；另一种是与车辆有关的疲劳标准。我国拥有辽阔的土地面积,并在高原、平原、盆地等地广泛进行分布,相应地会被气候和地壳运动等因素进行影响,相应地产生了各种路桥体,形成不同的载重性。在这一状况下,车辆也对各个区域的桥梁车辆疲劳荷载性能带来较大的影响。我国研究人员通过分析交通整体行业,编制一些规范,但较少涉及公路桥梁的分析。现有的公路钢桥规范缺乏合理性,具体是指钢桥拥有较大规模,相应疲劳研究缓慢,这一前提下,钢桥出现了显著的安全性和可靠性问题。相较于国际疲劳理论分析,我国有关规范相对落后,现实价值明显不足,公路桥梁车辆荷载仅对运营情况进行考虑,直接影响设计的精准度。为了改变这一现象,我国学者初步研究了公路桥梁车辆荷载与疲劳寿命的实践性。

一、车辆荷载优化高斯建模方法

（一）高斯混合模型基本原理

在概率知识与数理统计中,高斯混合模型至关重要,其对若干个高斯函数进行了结合,也可以是一种称之为状态数具有持续特点的模型,进一步拟合预估分布空间数据的状况。

利用高斯密度函数整体反映正态标准数据,普遍情况下,通常存在于数据空间的各个点不符合正态分布要求,此时通过融合不同的单一权重概率函数,也就是高斯模型成功拟合数据空间。基于理论角度分析,具备充足的混合数,多样化的车型与不同车辆的载货率形成十分复杂的车辆荷载模型。文献[1]证明高斯混合模型逐步接近概率密度分布函数,在分布车辆荷载样本概率中可以描述为高斯混合模型。这一模型采取了各种参数预估方式,其中普遍应用的是极大似然估计。其具体是在既定矢量训练状况下,获取最理想的参数模型,从而得到最大似然模型函数。但普遍情况下,在参数和极大近似然函数之间拥有十分复杂的非线性关系,无法通过一般方式得出极大点,且会形成较大的计算量。

一个总体样本中包含M个类型不同的个体样本Xi=（X1,X2,...,XM）,Xi代表一维随机变量,在样本空间所占比例为Wi,子样本形成具有独立特点的变量,第i个子样本与Pi（x）分布特点相符,进而形成有限混合模型,即:

车辆荷载与高斯混合分布相符。

（二）EM算法

EM算法对似然函数有效保证进而得到一个相对平衡点,凭借其高度稳定性与可用性得到十分广泛的应用。有关研究认为,设计初始数值GMM对迭代算法速率进行了严重的影响,同时,该算法属于一个对局部进行优化的搜索方法,一定程度产生局部性收敛,得到最佳解释,这也是搜索结果与初始化参数不同的原因；一般采取随机的初始简单方式,不能获得较好的使用效果,联系前人的经验教训,将均值算法结果作为初始化参数。

根据样本数据多权重和参数比值积极确定。对于多峰混合模型,训练已知样本的类标签严重不足或不能观测部分数据,被认定为典型不完全评价数据操作。由文献[2]了解到EM算法能对典型性不完全数据似然问题科学处理。该算法主要凭借一个快速迭代的计算极大似然程序对数据实行估算,每次迭代划分为两个环节,EM算法的估算如下。

一维空间观测数据Xi=（X1,X2,...,XM）参数极大似然估计表达式为：

公式（2）提取数据的过程中,仅能获取一部分参数数据,因此必须再一次构造完全数据类型。

强假设参数式方法为其创造了良好的性质：

（1）参数拥有非常有限的数量,一般比训练样例小,所以学习参数式方法相对比较简单；

（2）参数化处置了估计分布,搜索最优参数的过程限制于一个无关训练样例数目的低纬度空间,防止高维状况下出现维度灾难问题；

（3）在合理假设的情况下,相对于非参数方法有效减少了所需样本数量。

（三）高斯混合模型的优化

采取EM算法建立评估参数混合模型,并结合高斯分量数M实施,注意检验高斯分量数。在真实的状况中,数据样本包括未知的分布类型。严格划分观测样本为多个模型数量,从而对数据样本特性真实反映,模型也表现出复杂性。确定某一平衡点,在符合拟合模型精度前提下,提升混合模型自身便利性。对参数M数值合理明确时应注意模型的准确和便捷性,这也是模型改进的主要环节。

在信息统计中,已知数据观测样本十分复杂,故应建立衡量统计模型优良拟合准则,实现权衡所估计模型的复杂性及该模型拟合数据的优良性。通过AIC准则和BIC准则明确M参数,具体表达式为：

其中混合模型参数个数为m,样本观测向量长度为n,最大似然数值为 InL（x│M,wi,μσ2）。

二、标准疲劳车辆建模

（一）等效轴重

高斯混合模型真实体现分布公路车辆总重和轴重的概率,但在实际工程中直接运用,还必须有效的简化模型。计算简化是假定m辆等效模型车辆及统计同类车型对结构构件的疲劳损伤值基本相等。同时对车辆轴重和构件之间的应力变化科学设计,并制定线性数值关系,根据Miner准则及效力同等准则,等效轴重计算公式：

式中轴重随机变量为Pi；f（Pi）是轴重的高斯混合概率模型。

（二）等效轴距

通过文献数据分析了解所有车轴距分布的正态化,即:

其中,等效轴距为De,统计轴距为Di。

（三）实例分析

1.车型和轴距

在统计交通荷载过程中总样本为车流量,各种车辆类型代表任何一个由子样本组成的总样本。本文通过对南西路段承重数据动态监测,车辆以车轴数目为类型的划分标准,划分车辆具体包括C2、C3（A）、C3（B）、C4、C5、C6。由于桥梁通过普通轻型车辆时底缘钢筋形成的疲劳应力与极限强度要求完全不符,故可以不考虑这部分车辆形成的疲劳贡献。采取实时监测方法反映高速公路在一个月之内车辆荷载情况,总样本数为27838辆。通过分析样本可知,车流量明显高于C3（A）、C3（B）、C5。在这一路段通过偶数类型车辆,地区特色十分显著。结合对实际数据的统计,并结合公式计算各轴距形成的数据。

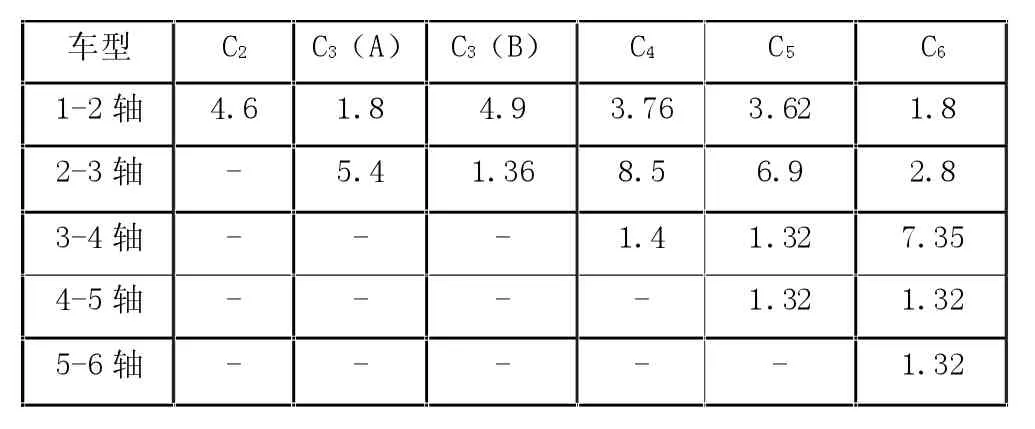
表1 典型车辆轴距统计（m）

2.轴重

比如建立C3（A）轴重荷载模型,对三轴轴重概率有效分析。通过计算可知,C3（A）一轴与二轴呈近似分布状态,同时与三轴轴重出现了巨大的差别。具体原因是C3（A）前两轴全部应用分布均匀的荷载。另外,C3（A）一轴与两轴概率呈双峰分布态势,轴重具体包括10t、20t和40t。对C3（A）建模程序不断重复,建立另外类型车辆轴重统计概率模型。对等效疲劳成功换算,得出疲劳车型在高速公路的相关标准。

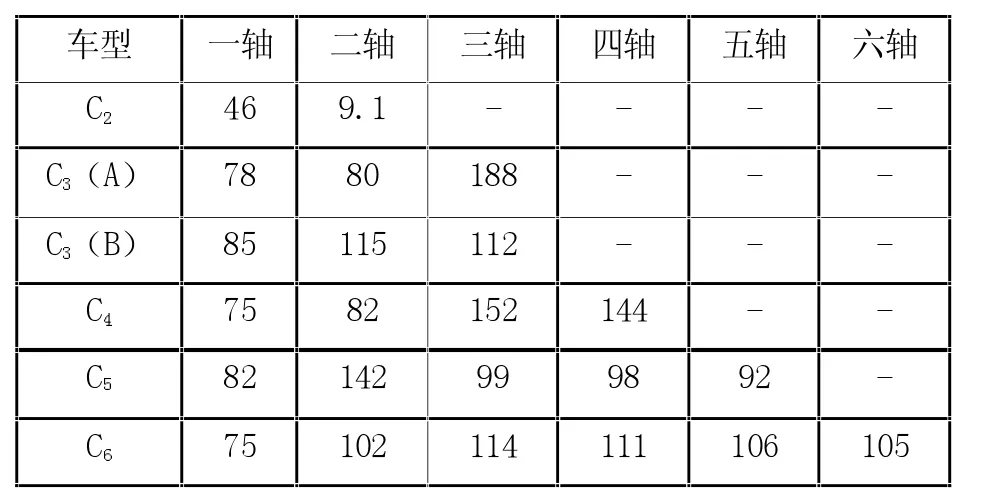
表2 典型车型等效疲劳车辆轴重kN

三、等效疲劳车辆作用下梁桥疲劳寿命评估

（一）Miner线性累计疲劳损伤准则

Miner准则由于并不牵涉加载疲劳顺序并对损伤疲劳数值进行准确计算,广泛推广应用在全国桥梁设计标准中。定义疲劳强度是通过循环使用疲劳应力数次后,材料由于疲劳产生断裂。横坐标在坐标轴上代表不断循环应力的具体次数,纵坐标代表疲劳应力,通过完全拟合获得材料曲线,表达式:

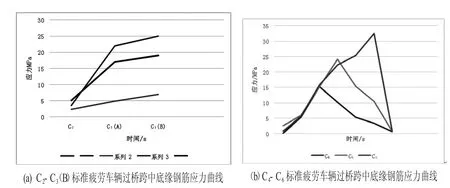
图1 C2-C6标准疲劳车辆过桥跨中底缘钢筋应力曲线

（二）高速某梁桥疲劳寿命评估

本文选择WIM对某段高速公路T梁简支工程作为研究对象。计算参考的有关参数：设计公路荷载Ⅰ级,计算跨径39.5m,底缘钢筋跨中一般牌号是HRB335。

通过有限元软件对各个等效典型性疲劳车辆过桥程序整体分析,简单绘制底缘跨中钢筋应力曲线,见图1。

采取雨流计数法准确计算车辆通过中桥梁底缘跨中钢筋截面疲劳应力中螺纹钢产生的疲劳强度,获取通过桥梁的各类车型形成的钢筋疲劳损伤值,见附表1。

在不考虑环境因素的情况下,在2015年11月梁桥通过车辆形成的疲劳损伤值5.5×10-5,未来交通量增加概率为5%,桥梁产生的疲劳寿命为89年。选择单峰荷载模型、多峰简洁荷载模型计算加载。由此可知,基于单峰荷载模型下桥梁产生82年疲劳损伤寿命,与多峰荷载模型的疲劳损伤时间对比前者相对较小,计算精度不佳。

四、结束语

社会经济的迅速发展,逐步凸显出公路桥梁的重要作用,但由于快速增加的交通量,人们也日益关注桥梁构件质量,特别是钢构件的疲劳问题。公路桥梁近几年由于疲劳破损经常发生意外事故,对人身财产带来巨大的损失。为了不断提升公路桥梁的安全性能,延长其应用寿命,本文联系EM算法和信息统计学中AIC和BIC准则,提出了高斯混合建模方法,逐步提升了概率模型的准确度与便捷性,有利于公路车辆建立科学、高效的荷载概率模型。结合WIM调查得到的数据,可以利用高斯混合建模法对车辆通过桥梁分布轴重概率密度准确描述,得到典型车辆分布轴重概率函数。根据疲劳等效损伤准则,基于高速公路建立疲劳车辆等效模型,便于公路桥梁设置疲劳荷载以及评价疲劳寿命。评估了某简支桥梁疲劳寿命,交通量设定为5%的增长率,桥梁疲劳寿命达到89年。在桥梁疲劳损伤寿命计算评价数值单峰荷载模型明显小于多峰荷载模型。

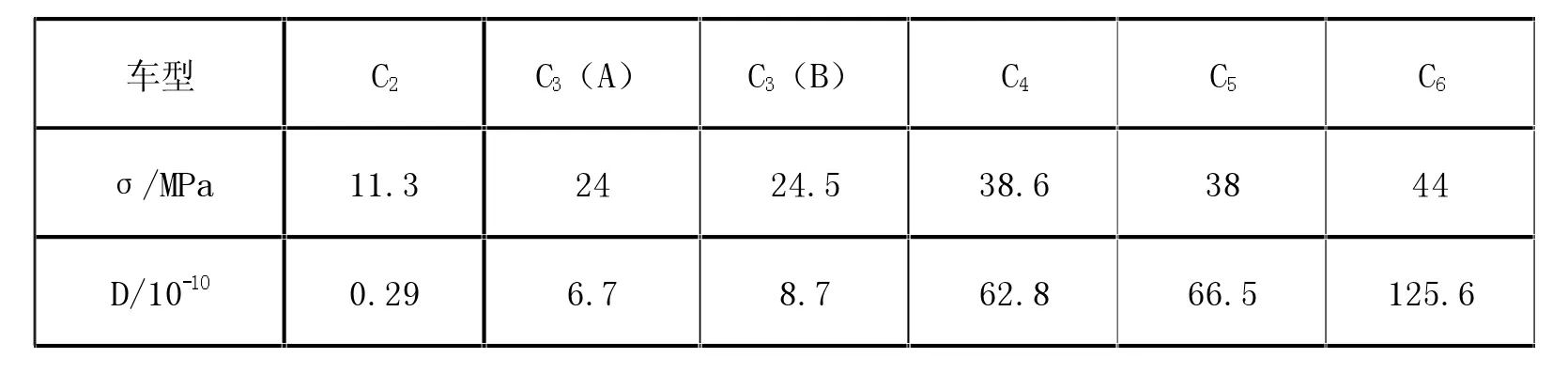
附表1 各种车型过桥对应的钢筋疲劳损伤数值