基于有限元网格尺寸效应影响的峰值应变修正研究

彭容新，陈爱军，贺国京，王解军



基于有限元网格尺寸效应影响的峰值应变修正研究

彭容新，陈爱军，贺国京，王解军

(中南林业科技大学 土木工程学院，湖南 长沙 410004)

对混凝土塑性损伤模型的单轴应力-应变关系、损伤变量、屈服准则和流动法则等进行阐述。利用ABAQUS对标准立方体混凝土试块模型采用不同网格尺寸进行计算，通过回归分析得到网格尺寸与本构模型峰值应变的函数关系。随后建立矩形截面单肢墩与双肢墩的有限元模型，基于上述函数进行损伤模型的峰值应变修正。并根据2个桥墩的有限元模型，设计并进行2个试验墩的试验研究。通过对比可见，调整峰值应变可有效消除网格尺寸对混凝土结构有限元分析的影响，ABAQUS塑性损伤模型在调整峰值应变后计算所得结果与试验结果更接近。且此方法对简单结构更为有效，而对于较为复杂结构，应视具体结构的复杂情况进行详细分析。

网格尺寸效应；塑性损伤模型；单调加载试验；非线性分析；钢筋混凝土桥墩

混凝土是以水泥为胶凝剂，结合粗细骨料、外加剂等形成的水硬性胶凝材料，是当今使用最广的建筑材料。但随着世界建筑与交通技术的不断发展，人们对混凝土结构的使用越加复杂、耐久性要求越高，特别是对于大跨度桥梁，其在长期荷载作用下的损伤与断裂受到人们的高度关注。上世纪60年代，Kachanov[1]首次在混凝土材料的研究中加入了断裂力学对其的影响。随后，Robotnov[2]引入损伤因子概念，其后，Leckie等[3−7]分别对损伤力学理论体系的形成作出了重要贡献。近20年来，随着计算机技术的不断创新，利用有限元方法对混凝土结构进行非线性分析，得到结构从开始受力直至破坏的全过程损伤演化是行之有效的。在相关参数设置合理的前提下，塑性损伤模型可用于混凝土结构或组合结构在往复荷载作用下的受力行为模拟，而弥散开裂模型只适用于结构在单调荷载作用下的力学行为分析。故相比ABAQUS中提供的混凝土本构模型，塑性损伤模型的破坏规则较为符合实际。除了混凝土本构关系，模型划分网格的尺寸对混凝土结构非线性分析的影响也极为显著。特别是对于混凝土结构的应力分析[8]，网格尺寸直接影响到有限元计算结果的精确度与准确性。国内外学者针对有限元分析网格尺寸效应问题的研究已有部分成果，DONG[9]应用结构力学基本原理，采用有限元分析计算焊趾处的结构热点应力，提出网格不敏感结构应力方法。邹超英等[10−11]以拱坝坝体为例，研究有限元单元类型、网格数量、自由度数量与能量误差之间的关系。杨令强等[12−14]利用自适应有限元对国内3座高拱坝进行研究，探讨高拱坝的应力状态、等效应力与等参单元的大小和形状之间的关系。尽管网格尺寸效应对混凝土结构有限元分析的影响取得了部分研究成果，但研究的主要内容多为焊接、高拱坝的网格划分，而关于混凝土结构非线性分析的网格尺寸效应，特别是有关桥梁墩柱的研究可查询资料很少。本文利用ABAQUS对不同网格尺寸的标准立方体混凝土模型进行分析，并采用回归分析得到网格尺寸与损伤模型的函数关系。最终通过对比桥墩模型的承载力试验与有限元计算结果，验证对混凝土的峰值应变进行修正，混凝土结构非线性分析准确性的提升效果显著。

1 混凝土塑性损伤模型

1.1 破坏准则

1.2 屈服准则

屈服面定义了塑性损伤模型的临界应力状态(如图2所示)。现今，已提出大量屈服准则用来解释构件受拉受压状态下的材料强度演变。对于混凝土塑性损伤理论，最初由Lubliner等[15]提出经典理论，随后Lee等[16]对其进行了进一步的完善。其中，混凝土塑性损伤模型的屈服面函数[17]为：

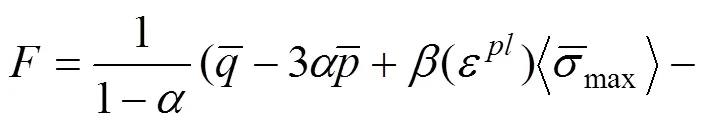
式中：为Mises等效应力；为静水压力；为最大有效应力；为混凝土双轴抗压强度；为混凝土单轴抗压强度；为混凝土单轴抗拉强度；Kc为控制混凝土屈服面在偏平面上的投影形状，不同参数对应的偏平面的屈服面如图3所示。

图2 在平面应力状态下的屈服面

1.3 流动准则

塑性损伤模型由潜在流动函数的流动规则来决定材料塑性变形的方向和大小。考虑到与金属材料的差异，该模型选用非关联流动法则，且采用Drucker-Prager型的双曲线模型形式。如图4所示，塑性应变增量与塑性势函数相一致，并由其可得到混凝土在子午面内的膨胀角与偏心率。其中塑性势函数为：

式中：φ为混凝土屈服面在强化过程中的膨胀角，根据相关研究成果，混凝土的膨胀角的取值范围为 30°~42°；e为混凝土塑性势函数的偏心距，可取 为 0.1。

图4 在子午面内的膨胀角与偏心率

2 网格尺寸效应

2.1 有限元模型的建立

根据以上所述塑性损伤模型，混凝土抗压强度取试验结果，设置膨胀角为35°，偏心率取0.1，初始等效双轴抗压强度与初始等效单轴抗压强度的比值取1.167，受拉与受压子午线应力比值为0.666 7，黏性参数取0.001。混凝土损伤因子及等效塑性应变参考《混凝土结构设计规范》(GB50010—2010)。

混凝土选用C3D8R单元，即八节点减缩积分三维实体单元。网格划分采用扫掠方法，网格以六面体为主。边界条件为试块底面固结，在试块顶面进行位移控制加载。

2.2 计算结果分析

为验证网格尺寸对混凝土结构非线性分析的影响，同时将标准立方体混凝土划分成8，27，64，216，512，1 331和1 728个单元，并进行单轴拉压的力学性能试验模拟。计算所得单轴受力荷载-位移曲线如图5所示。极限荷载计算值随模型网格尺寸增大而增大，且随着网格尺寸的不断减小极限荷载趋于定值。而单轴受拉极限荷载的减小程度要远大于单轴受压。对于不同网格尺寸的标准混凝土结构的计算结果，除极限荷载点差别较大外，随着位移的增大，荷载的变化趋势基本一致，并于最大位移的位置相重合。同时随着网格尺寸的不断增大，曲线的下降趋势变缓，且计算效率与收敛性较好。

根据以上计算结果，得到不同网格尺寸的标准立方体混凝土损伤云图如图6所示。由图6可知，计算所得受压损伤结果与试验结果一致，且随着网格尺寸的减小，计算所得结果更加趋于实际结果。故对混凝土结构进行非线性分析时适当减少模型划分网格的尺寸，其计算结果的准确性显著提升。

(a) 单轴受拉；(b) 单轴受压

(a) 75 mm网格；(b) 50 mm网格；(c) 37.5 mm网格；(d) 25 mm网格；(e) 18.75 mm网格；(f) 13.6 mm网格；(g) 12.5 mm网格

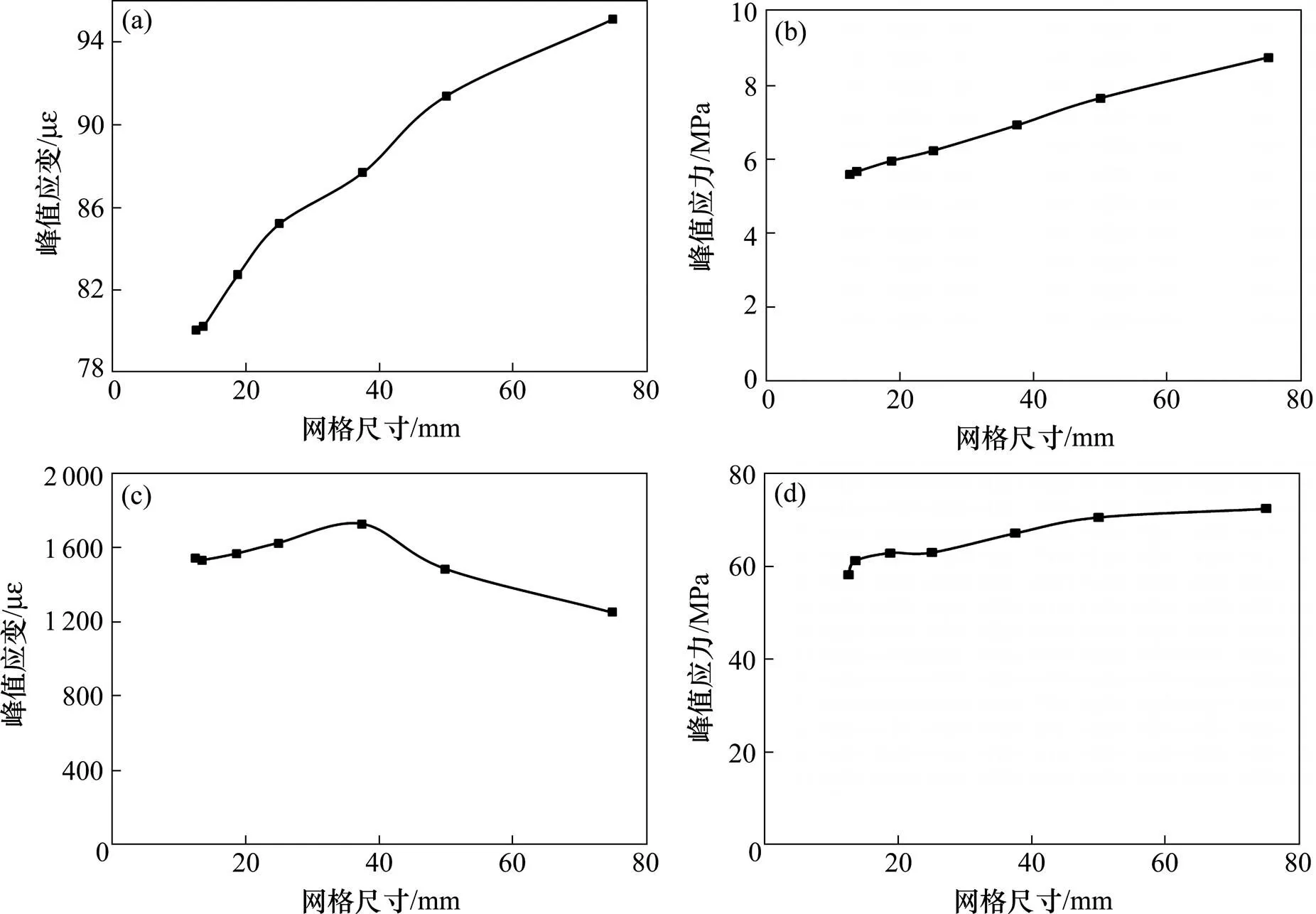
(a), (b) 单轴受拉；(c), (d) 单轴受压

由受压损伤云图6可以看出，随着网格尺寸的减小，立方体混凝土的损伤程度首先减小至3.87%，随后又逐渐增大，且在网格尺寸达到13.6 mm与12.5 mm时，混凝土结构受压损伤程度基本一致。同时随着网格尺寸的减小，受压损伤向立方体混凝土的顶部发展，且破坏位置更加具体。同时，由图6可以看出，标准立方体混凝土受压破坏出现明显的斜裂缝，整体压碎现象明显。

2.3 峰值应变修正法

由以上计算结果可以看出，对于相同的构件，选取不同的网格尺寸，有限元计算所得荷载、位移及构件的应力与损伤分析相差较大。网格尺寸效应对混凝土构件有限元计算的准确性有很大影响。

由断裂能的释放原理,混凝土结构在断裂过程中所释放的能量与网格尺寸无关[18]。而单元网格尺寸越小，混凝土结构的裂缝开展越快，其构件的能量释放能力越小。故在相同的破坏准则下，当网格较小时，在较小的荷载作用下，小单元的应力往往非常大，这使得构件更加容易破坏，计算所得构件的承载力相对就较小。

由有限元计算结果的对比分析可知，计算所得峰值应变与本构模型的峰值应变有所区别。因此，为消除网格尺寸效应对混凝土结构非线性分析影响，保证混凝土构件非线性分析的准确性。本文尝试采用调整混凝土本构模型峰值应变的方法，来消除网格尺寸对混凝土结构非线性分析的影响。

通过以上计算所得标准立方体混凝土的荷载−位移曲线，可得标准立方体混凝土的峰值应力应变−网格尺寸曲线如图7所示。由图7可知，拉应变与拉应力随着网格尺寸的增加变化趋势明显，网格尺寸对混凝土本构模型的峰值拉应变影响较大。

当网格尺寸较大时，网格尺寸对混凝土峰值压应变的影响亦非常明显。故根据计算峰值应变、网格尺寸及本构模型的破坏准则，通过回归分析得到峰值应变与网格尺寸的关系如下：

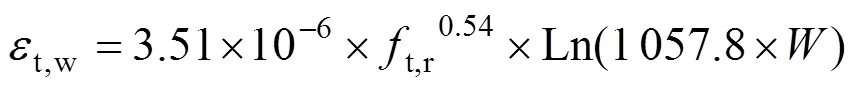
其中，混凝土的峰值应变不是一个定值，而是随着网格尺寸的增大而不断变化的，且式中同时计入了混凝土塑性损伤模型的破坏准则，故通过该式可直接进行混凝土峰值应变的计算，并完成峰值应变的修正。

3 网格尺寸效应的试验研究

3.1 试验概况

3.1.1 试验墩设计

根据现有钢筋混凝土桥墩的截面特性，设计制作2个试验墩，分别为单肢墩与双肢墩。DZ-01为矩形截面单肢墩，截面尺寸为540 mm×360 mm；SZ-02为双肢墩，试验墩底座设计为1.2 m长×0.7 m宽×0.5 m高，在浇筑时预留好4个Φ100 mm地锚螺栓孔，试验时通过地锚螺栓锚固于刚性地基。如图8所示。

(a) DZ-01(矩形截面实体墩)；(b) SZ-02(双肢墩)

试验墩采用C50混凝土，一次性浇筑完成，2 d后脱模，自然养护28 d，并分别同条件养护3组标准试块，正式加载前对试块进行力学性能试验。其中DZ-01混凝土强度均值为51.70 MPa，SZ-01混凝土强度均值为50.40 MPa。纵筋采用HRB335热轧钢筋；箍筋采用HRB235热轧钢筋，钢筋材料性能试验值与标准值强度基本一致。

3.1.2 试验墩加载方案

试验加载设备如图9所示。竖向荷载通过竖向千斤顶一次加载到位，竖向千斤顶置于墩顶与反力架横梁之间，并在墩顶与千斤顶之间设置滑轮小车，以保证竖向力随着墩顶的侧向移动而移动。水平荷载采用电液伺服控制系统加载，作动器最大输出力为250 kN。在正式加载前先进行预加载，于墩顶施加100 kN的竖向荷载，并施加预计开裂荷载10%~30%的水平荷载。在2次预加载之后，再施加试验墩各等级荷载。根据作动器的性能，采用荷载控制加载。其中整体墩每级水平荷载为7 kN，空缝双肢墩模型每级水平荷载为10 kN加载。且每级等幅加载直到试验墩的抗力下降到最大抗力的85%时，停止继续加载，以防试验墩突然倒塌。

在试验墩浇筑前，于试验墩混凝土、纵筋与箍筋上均预设钢筋应变计，通过静态电阻应变仪进行测试。并于加载前在试验墩墩顶安装位移计，测试墩顶的水平位移。同时在试验墩表面粉刷乳胶漆以便观察桥墩裂缝开展及破坏过程。

3.2 试验墩有限元模型的建立

如图10所示的有限元模型中，混凝土选用C3D8R单元，即8节点减缩积分三维实体单元；纵筋和箍筋单元类型采用T3D2，即2节点线性三维桁架单元。边界条件采用墩底基座固结。为模拟试验中的加载方式，分别在有限元模型的墩顶面竖向和侧面顺桥向各设置1个加载控制点，以模拟墩顶加载的竖向力与水平推力，并将该作用点与混凝土所对应的截面进行耦合。对于箍筋和纵筋，采用Embeded技术将其内嵌到整个混凝土试验墩模型中，使纵筋和箍筋与混凝土共同工作(如图10(b))。钢筋为各项同性材料，采用理想弹塑性模型，混凝土采用上述标准立方体混凝土所用的本构数据。并分别以60，45，30和15 mm的网格尺寸进行计算分析。

(a) 试验墩加载示意图；(b) 试验墩加载现场

(a) 试验墩模型(15 mm网格)；(b) 接触模拟

3.3 结果分析

3.3.1 试验墩破坏形态分析

如图11所示为2个试验墩的破坏形态。对于单肢墩(DZ-01)如图11(a)所示，当墩顶水平加载至105 kN时，试验墩受拉侧出现3条水平裂缝，其分别距墩底为10，30与45 cm，且钢筋与混凝土的应变于此时迅速增大。随后当加载达到145 kN时，DZ-01又出现2条水平裂缝，其中一条距墩底85 cm。同时，桥墩受压侧出现局部剥落。其后的试验，该桥墩墩顶加载到极限荷载，即135.95 kN。在此过程中，水平裂缝不断发展到桥墩的侧面，但没有产生新的裂缝。

(a) DZ-01；(b) SZ-02

在相同水平荷载作用下，双肢墩(SZ-02)的裂缝与损伤相比DZ-01更加严重，且分布面积更大，破坏更为严重。其开裂荷载为60 kN，为 DZ-01的57.14%，最大承载能力为105 kN，只有DZ-01的72.41%。

3.3.2 试验墩墩顶荷载-位移曲线

根据试验结果与有限元计算结果(以15 mm网格为例)如图12所示可得，利用ABAQUS进行有限元分析所得计算结果与试验结果基本一致，且调整混凝土峰值应变后，有限元计算结果与试验结果更为接近。单肢桥墩相比双肢桥墩的承载力较大，且由于试验墩为矮墩的缩尺模型，故在相同截面下，双肢墩的延性并未得到明显的提升。

表1为该桥墩不同网格尺寸的极限承载能力与延性系数的有限元计算与试验结果，从表1可得，对于单肢墩，通过峰值应变的调整，试验所得承载力结果相比计算结果的最大误差由8.3%减少到1.9%，延性相比计算结果的最大误差由38.4%减少到15.8%。而对于双肢墩，通过峰值应变的调整，试验所得承载力结果相比计算结果的最大误差由8.8%减少到3.6%，延性相比计算结果的最大误差由24.3%减少到17.6%。

本文所提出的混凝土本构模型峰值应变修正法对混凝土结构非线性分析的效果显著，且对单肢墩结构的影响更为明显，而对双肢墩结构，由于结构形式对网格划分的影响较大，网格划分更为复杂，仅通过调整峰值应变，对计算的精确提升并不明显。

(a) SZ-01(整体墩)；(b) SZ-02(双肢墩)

而对于延性系数，其经过本构模型的调整，误差依然较大。究其原因，主要还是试验加载及固定装置与试验墩无法完全固定，使得加载作动器在进行试验时所测的的荷载数据出现误差所致。

表1 桥墩承载能力与延性计算结果

注：1. 表中模型编号栏的括号中“N”表示未调整的模型，“Y”表示调整的模型； 2. 表中“F”表示极限承载力，“”表示延性系数

4 结论

1) 相同模型，选取不同的网格尺寸，有限元计算所得荷载、位移及构件的应力与损伤分析结果相差较大。网格尺寸效应对混凝土构件非线性分析的准确性影响很大。

2) 对于标准立方体混凝土结构采用不同网格尺寸进行计算，除极限荷载点差别较大外，随着位移的增大，荷载的变化趋势基本一致。同时随着网格尺寸的不断增大，荷载的下降趋势逐渐变缓，且计算效率与收敛性更好。应力分布及受压损伤计算结果与试验结果相一致，且随着网格尺寸的减小，计算结果与试验结果更加相近。

3) 有限元分析得到的抗推极限承载力及延性系数与试验所得结果基本一致，且通过调整混凝土的峰值应变，对混凝土结构非线性分析准确性的提升效果显著。

4) 对单肢墩这种简单结构，通过峰值应变修正来减少有限元网格划分尺寸效应的影响是十分有效的。而对于结构相对复杂的双肢墩，不能简单地通过峰值应变修正来减少网格尺寸效应的影响以达到提高计算精度目的，应视具体结构的复杂情况进行详细分析。

[1] Kachanov L M. Time of the rapture process under creep conditions TVZAkad[J]. Nauk S S R Otd Tech Nuak, 1958, 8: 26−31.

[2] Rabonov Y N. Creep rapture[C]// Proc 12, Inter Congress, Appl Mech Stanford, Springer Berlin, 1969.

[3] Leckie F A, Hayhurst D R. Creep rupture of structure[C]// Proc R Soc A, 340, 1974.

[4] Hult J. Damage induced tensile instability[C]// Trans. 3rd AMIRT, London, 1975.

[5] Lemaitre J. Application of damage concepts to predict creep-fatigue failure[J]. J Eng Mat Tech, ASME, 1979, 101(1): 202−209.

[6] Kajcinovic D. Continuum damage theory of brittle materials[J]. J Appl Mech, 1981: 809−824.

[7] Sidoroff F. Discription of anistropic damage application to elasticity[C]// IUTAM Colloquium, Physical Nonlinearities in Structural Analysis, 1981: 237−244.

[8] 崔焕平. 混凝土非线性有限元分析与网格尺寸效应[D].郑州: 郑州大学, 2004. CUI Huanping. Nonlinear finite element analysis of concrete and grid size effect[D]. Zhengzhou: Zhengzhou University, 2004.

[9] DONG P. A structural stress definition and numerical implementation for fatigue analysis of welded joints[J]. International Journal of Fatigue, 2001, 23(10): 865−876.

[10] 邹超英, 曾海军. 单元类型和节点数量对拱坝坝体应力的影响[J]. 科学技术与工程, 2013, 13(26): 7894− 7897. ZOU Chaoying, ZENG Haijun. Influence of element type and number of nodes on stress of arch dam body[J]. Science Technology and Engineering, 2013, 13(26): 7894−7897.

[11] 邹超英, 苏志敏, 曾海军, 等. 拱坝有限元分析网格剖分方案研究[J]. 南水北调与水利科技, 2011, 9(1): 47− 49. ZOU Chaoying, SU Zhimin, ZENG Haijun, et al. Research on grid subdivision scheme for finite element analysis of arch dam[J]. South-to-north Water Diversion and Hydro Technology, 2011, 9(1): 47−49.

[12] 杨令强, 练继建, 张社荣, 等. 随机有限元与最大熵法联合求混凝土拱坝可靠度[J]. 水利水运工程学报, 2003(2): 24−28. YANG Lingqiang, LIAN Jijian, ZHANG Sherong, et al. The reliability of concrete arch dam by stochastic finite element and maximum entropy method[J]. Journal of Water Conservancy and Waterway Engineering, 2003(2): 24−28.

[13] 杨令强, 马静, 陈祖坪. 利用自适应有限元研究高拱坝的应力控制标准[J]. 水利水电技术, 2008(4): 53−55. YANG Lingqiang, MA Jing, CHEN Zuping. The stress control standard of high arch dam is studied by adaptive finite element method[J]. Water Conservancy and Hydroelectric Technology, 2008(4): 53−55.

[14] 杨令强, 马静, 陈祖坪. 自适应有限元在拱坝破坏追踪中的应用[J]. 水力发电学报, 2008(3): 48−53. YANG Lingqiang, MA Jing, CHEN Zuping. Application of adaptive finite element method in failure tracking of arch dams[J]. Journal of Hydroelectric Power, 2008(3): 48−53.

[15] Lubliner J, Oliver J, Oller S, et al. A plastic- damagemodel for concrete[J]. International Journal of Solids and Structures, 1989, 25(3): 299−326.

[16] Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics Division-ASCE, 1998, 124(8): 892−900.

[17] Yin Chi, Min Yu, Le Huang, et al. Finite element modeling of steel-polypropylene hybrid fiber reinforced concrete using modified concrete damaged plasticity[J]. Engineering Structures, 2017, 148: 23−35.

[18] 沈聚敏, 王传志, 江见鲸. 钢筋混凝土有限元与板壳极限分析[D]. 北京: 清华大学, 1993. SHEN Jumin, WANG Chuanzhi, JIANG Jianjing. Finite element analysis of reinforced concrete and plate-shell limit[D]. Beijing: Tsinghua University Press, 1993.

(编辑 阳丽霞)

Study on peak strain correction based on the impact of finite element mesh size effect

PENGRongxin, CHEN Aijun, HE Guojing, WANG Jiejun

(School of Civil Engineering, Central South University of Forestry and Technology, Changsha 410004, China)

Firstly, the uniaxial stress-strain relation, damage variable, yield criterion and flow rule of the plastic damage model of concrete were expounded. Then, ABAQUS was used to calculate the standard cubic concrete sample block model with different mesh size, the function relation between the mesh size and the peak strain of the constitutive model was obtained by regression analysis. Then the finite element model of single pier and double pier with rectangular section was established, and the peak strain of damage model was corrected based on the above function. According to the finite element model of two piers, two test piers were designed and studied. By contrast, adjusting peak strain can effectively eliminate the influence of mesh size on the finite element analysis of concrete structure, and the results obtained by ABAQUS plastic damage model in adjusting peak strain are closer to the experimental results. And this method is more effective for simple structure, but for more complex structure, it should be analyzed in detail according to the complexity of concrete structure.

mesh size effect; plastic damage model; monotonic loading test; nonlinear analysis; reinforced concrete pier

10.19713/j.cnki.43−1423/u.2018.12.018

O242.21

A

1672 − 7029(2018)12 − 3148 − 10

2017−11−03

国家自然科学基金资助项目(51178473)；湖南省交通科技计划项目(201526)

陈爱军(1973−)，男，湖南邵阳人，副教授，博士，从事大跨桥梁施工监控及桥梁新型结构形式研究；E−mail：992357035@qq.com