近断层脉冲方向性对大跨斜拉桥地震响应的影响

陈志强，郑史雄，陈志伟，洪成晶，李晰

近断层脉冲方向性对大跨斜拉桥地震响应的影响

陈志强，郑史雄，陈志伟，洪成晶，李晰

(西南交通大学 土木工程学院，四川 成都 610031)

由于近断层地震动脉冲特性在不同方向上差异明显，以集集地震中典型脉冲地震记录为例，比较地震动峰值加速度PGA和峰值速度PGV在各个方向上的变异性；基于连续小波变化识别出最强脉冲能量所对应的方向，比较最强脉冲方向上地震动与初始地震记录的2条水平分量脉冲性的差异；以某大跨斜拉桥为例，研究近断层地震动脉冲方向性效应对其地震响应的影响。研究结果表明：近断层脉冲地震动的峰值加速度PGA和峰值速度PGV在各个方向上差异明显，通过旋转变换以后PGA和PGV的变异性分别达到30%和70%；基于连续小波变换识别出的最强脉冲方向与PGV最大值所在的方向基本重合，最强脉冲方向上地震动的反应谱和脉冲幅值都要明显强与实测地震动记录的2条水平分量；最强脉冲方向上地震动作用下大跨斜拉桥的地震响应明显要大于实测地震记录2条水平分量作用下的结果，在近断层地区的大跨斜拉桥抗震分析时应该以最强脉冲方向上的地震动作为输入，如果直接采用实测地震记录水平分量作为地震输入则将低估桥塔和主梁的位移响应可达到45.4%和40.2%。

脉冲方向性；连续小波变换；大跨斜拉桥；地震响应

大跨度斜拉桥由于其造型美观，跨越能力较强，近年来在公路和铁路的跨江、跨海工程中都得到了较多的运用。主跨1 088 m的苏通长江大桥、杭州湾跨海大桥中跨度448 m的主桥都已经建成通车，主跨1 092 m沪−通长江大桥、主跨518 m的公安长江大桥等一大批大跨度斜拉桥也正在如火如荼建设当中。对于这类大跨度斜拉桥而言，由于其跨度较大，刚度较低，结构自振周期较长，长周期地震作用对其影响尤为突出。近断层脉冲地震动是最为典型的一类长周期地震动。由于滑冲效应和前场方向性效应的影响，其速度时程中包含有明显的长周期、高幅值脉冲[1]。这种速度脉冲会对地震动中长周期段的反应谱产生显著的放大效应[2]，特别是当结构的自振周期和脉冲周期T接近时，结构的地震需求可能会急剧的增大。对于大跨度斜拉桥这种特殊结构，由于其自振周期较长，对结构其控制作用的振型较多，近断层脉冲地震记录中所含的长周期、高幅值脉冲更容易使其产生共振效应，从而对其地震响应产生较为不利的影响。近年来已经有不少学者进行了相关研究。徐艳等[3]通过等效模态法将斜拉桥简化为单自由度体系，提出了脉冲地震作用下斜拉桥地震响应的简化计算方法；LI等[4]提出了近断层脉冲地震动分解−叠加的合成方法，然后以苏通大桥为例，研究了滑冲效应和前场方向性效应对产生的2类脉冲地震动对大跨度斜拉桥地震响应的影响；李帅等[5]以集集地震为例，根据地震动测站位置与断层的空间位置关系，将地震动分为破裂前方区域(FD)、破裂区域(MD)和破裂后方区域(BD)，研究了近断层地震动的空间分布对斜拉桥地震响应的影响；Shrestha[6]研究了尼泊尔近断层区域内的Karnali斜拉桥的地震响应，详细研究了近断层竖向地震动对其地震响应的影响。以上成果虽然考虑到了近断层地震动速度脉冲效应的影响，在一定程度上丰富了近断层地区大跨度斜拉桥抗震设计理论，但是目前的研究都没有考虑到近断层脉冲地震动的方向性。然而，常志旺[7]的研究表明近断层脉冲地震动存在显著的方向性，脉冲型地震动的两条水平分量经过旋转变换后脉冲特性可能会消失，非脉冲地震动的两条水平分量经过旋转变换后也有可能变为脉冲型地震动。YANG等[8]的研究表明近断层最强脉冲方向上地震动的反应谱和能量都要明显大于垂直于断层和平行于断层2个方向的地震动分量。鉴于此，本文以台湾集集地震典型脉冲地震记录为例，基于连续小波变换[9]确定其最强脉冲方向，比较各个方向上地震动脉冲特性的差异，最后以某一大跨度斜拉桥为例，详细研究近断层脉冲地震动的方向性对大跨度斜拉桥地震响应的影响，从而为近断层地区大跨度斜拉桥的抗震设计提供参考。

1 近断层脉冲地震动的方向性

1.1 近断层脉冲地震动峰值参数的方向性

对于1组实测的地震记录，其包含2条水平分量和1条竖直分量。在进行结构地震响应分析时，通常以实测地震动的最大水平分量最为地震动输入。由于地震发生时地震记录测站和断层空间位置的随机性，实测的2条水平分量并不一定是该位置处所受到的最强地震作用。为了研究地震动的方向性，通常可以采用平行四边形法则对地震动的2条水平分量进行旋转变换，从而得到不同方向上的地震动水平分量，其计算式为[7]

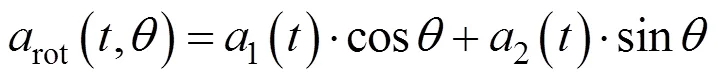
对于同一个测站的2条水平分量，通过不断变化的值就可以获得任意方向上的地震记录，从而研究地震动的方向性。

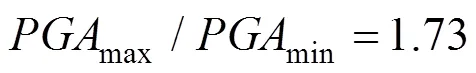
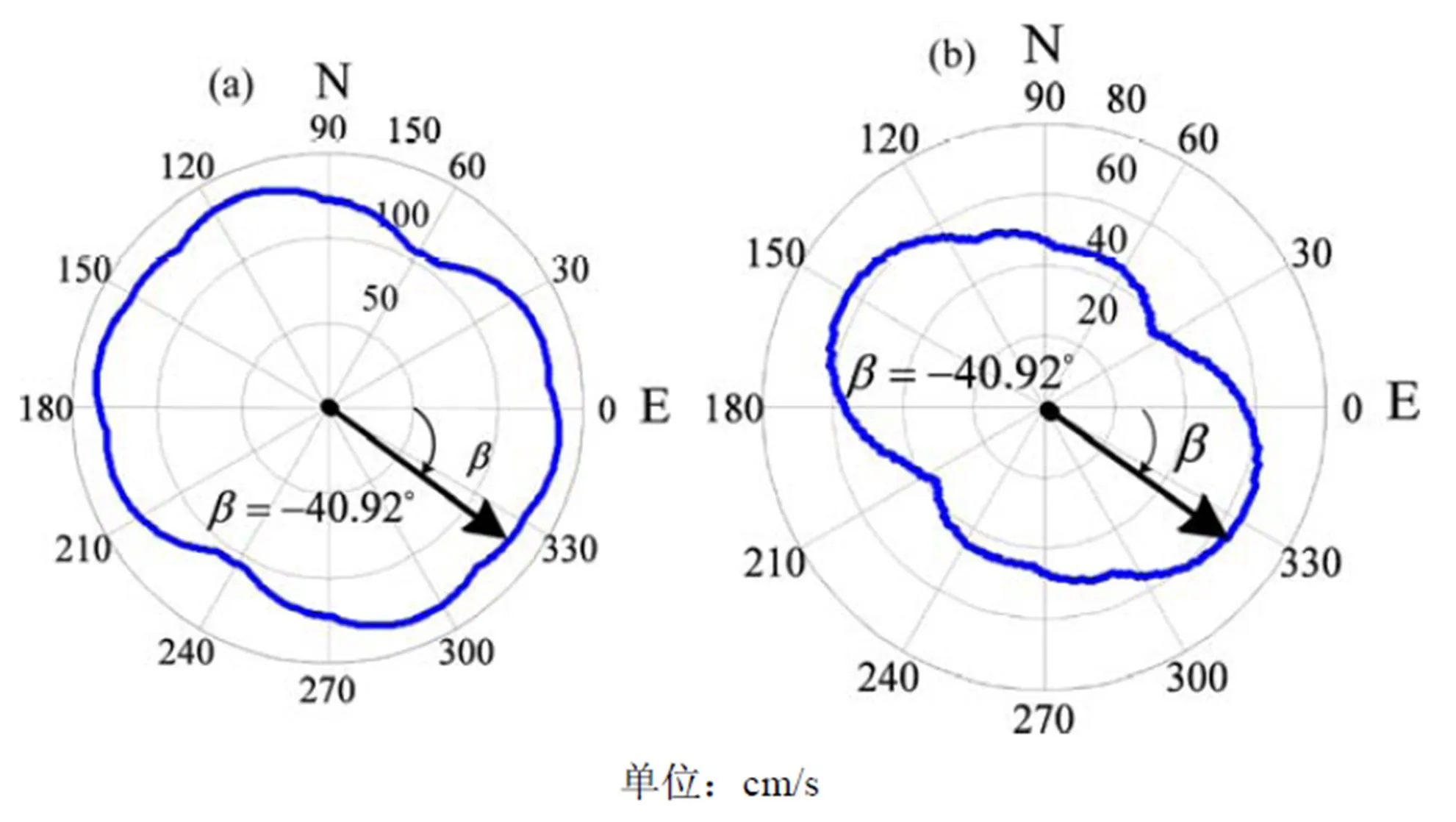
(a) PGA分布图；(b) PGV分布图

1.2 基于连续小波变换最强脉冲方向的确定

对于近断层脉冲地震动而言，不仅其峰值参数在各个方向差异显著，而且其脉冲特性在各个方向也有显著变化[9]，同一个测站的2条水平地震记录经过旋转变换后，其脉冲性可能消失，转化为非脉冲地震动。这在过去的多次研究中都得到了证 实[7, 10−12]。为了获得脉冲特性最为显著的方向(即最强脉冲方向)，Shahi等[10]基于连续小波变换提出了一种确定最强脉冲方向的高效方法，其首先对地震动的2条水平分量进行连续小波变换，然后将2条水平分量的小波系数进行线性组合，由此得到任意方向的地震动小波系数，最后以小波系数最大的方向作为地震动的最强脉冲方向。任意时刻时的小波基函数为

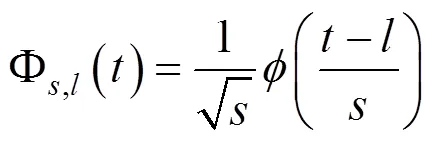
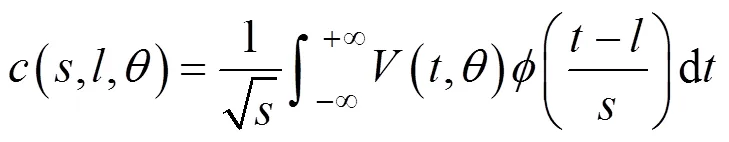
将式(1)代入，可得

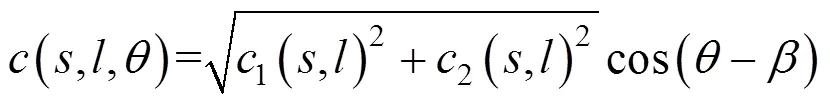
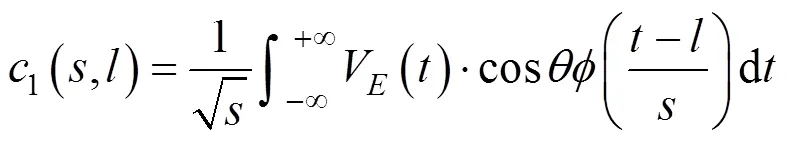
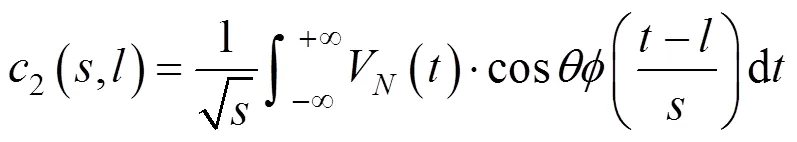
由此可计算最强脉冲方向

最强脉冲方向确定后，将EW和NS 2条水平地震记录按照式(1)进行旋转变换，即可得到最强脉冲方向上的地震记录。

这里以集集地震TCU036测站为例，按照式(2) ~(9)求得其最强脉冲方向为−40.92°，最强脉冲方向与峰值加速度和峰值速度的分布关系如图1所示。东西向、南北向以及最强脉冲方向3个方向上地震记录的速度时程和按照小波分析[12]提取的脉冲时程如图2所示，加速度反应谱(阻尼比=5%)如图3所示。

图1中可以看出，按照连续小波变换确定的最强脉冲方向上地震动的峰值加速度虽然较大，但并不是PGA最大值所在方向。该最强脉冲方向与峰值速度PGV最大值所在的方向基本重合，这主要是由于最强脉冲方向的确定就是按照地震动速度时程确定的，按照该方法确定最强脉冲时程是综合考虑了各个方向上地震动峰值速度PGV、脉冲周期以及脉冲持时等因素的影响。因此，按照连续小波变换确定的最强脉冲方向与峰值速度PGV最大值所在的方向基本重合。

(a) TCU036-E；(b) TCU036-E；(c) TCU036-STO

图2中可以看出，虽然这3条地震水平分量都为脉冲型地震记录，然而其脉冲幅值p和脉冲周期p[12]存在显著差异，与东西向、南北向地震记录相比，最强脉冲方向上地震动的脉冲幅值也明显要更大，脉冲周期明显更短，能量更为集中。由此说明了相比于原始的2条地震动水平分量，最强脉冲方向上地震动的脉冲特性将更为显著。

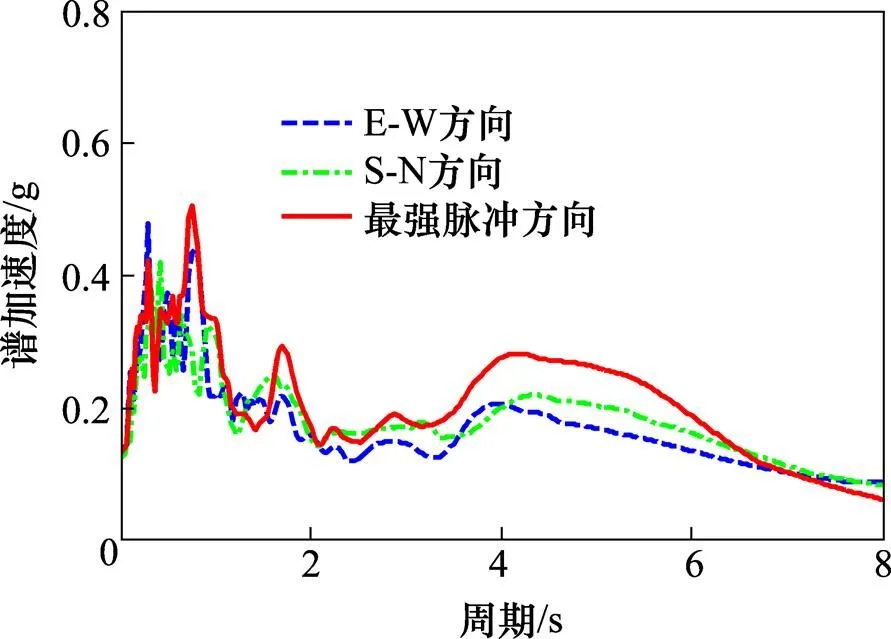
图3 不同方向上地震动加速度反应谱

此外，从图3中可以看出，与东西向和南北向2条原始水平地震记录相比，最强脉冲方向上地震动反应谱不仅在1.6~6.5 s的长周期范围内要更大，而且在0~1 s的高频段，最强脉冲方向上地震动反应谱也更大。只有在1.3 s附近的局部位置处，其才略微减小，这与YANG等[8]分析的结果完全一致。对于大部分工程结构而言，其自振周期都位于0~6.5 s的频段内，因此在最强脉冲地震激励下，桥梁结构的地震响应可能会明显增大。

2 工程背景与桥梁动力模型

2.1 工程背景及桥梁结构建模

以某双塔双索面特大跨斜拉桥为工程依托，其跨径布置为51+91+300+91+51 m，桥梁全长584 m (含两端主桥梁缝)，边、中跨之比为0.473。主梁为预应力混凝土箱型梁，材料为C55混凝土，截面类型为单箱单室等高截面，截面全宽13 m，中心处梁高4 m。桥塔采用钻石型塔，塔高120.5 m，梁顶以上塔高75 m，材料为C50混凝土。斜拉索采用抗拉标准强度1 670 MPa平行钢丝拉索，全桥共有72对(144根)，索面呈扇形布置。支撑体系采用半漂浮体系，即主梁在塔上设置双向滑动球形钢支座，墩上设置单向滑动球形钢支座，塔梁间设置纵向阻尼器。整个桥梁结构布置如图4所示。

图4 斜拉桥立面布置图

基于ANSYS通用有限元软件建立全桥有限元模型进行动力分析，主梁和桥塔采用BEAM188单元模拟，边墩和辅助墩采用BEAM44单元进行模拟，拉索采用LINK8单元进行模拟。主梁与主塔和辅助墩之间的支座采用节点耦合来实现，塔底和墩底均为固结。桥梁结构有限元模型如图5所示。

2.2 桥梁结构动力特性

基于ANSYS中的Modal 模块，采用Lanczos方法计算该斜拉桥的前50阶模态的振型和频率。相对于连续梁桥和连续刚构桥而言，大跨度斜拉桥结构体系较柔，自振周期较长，高阶模态的参与系数较大。限于文章篇幅所限，表1仅列出了前5阶模态的周期、频率和振型。从表1可知，该算例斜拉桥1阶模态为全桥纵飘，自振周期为5.99 s，属于长周期结构，结合图3中的地震动反应谱，1阶模态刚好落在脉冲周期附近，近断层地震动的速度脉冲效应将对其地震响应产生明显的影响。

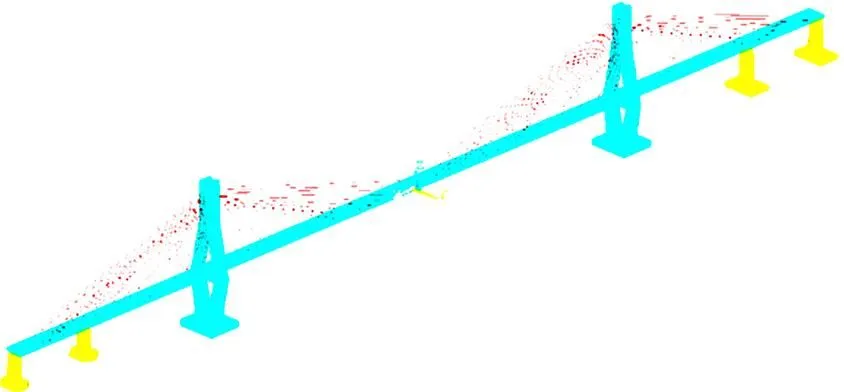
图5 桥梁结构有限元模型

表1 桥梁动力特性

3 考虑脉冲方向性的大跨斜拉桥地震响应分析

为了研究近断层脉冲方向性效应对大跨度斜拉桥地震响应的影响，将图3中的东西方向(EW)、南北方向(NS)和最强脉冲方向(Strongest Pulse Orientation，SPO)上的地震记录分别作用于该算例桥梁数值模型，通过时程分析获得桥梁结构地震响应。由于各个方向上地震动的峰值参数都不同，为了保持各个方向上地震动的结构效应，这里均采用原始地震记录，不做调幅处理。

另外，为了量化近断层脉冲方向性对大跨度斜拉桥地震响应的影响程度，本文定义了脉冲方向性对桥梁结构地震响应的放大系数F

3.1 桥塔地震响应

图6~7分别给出了上述3条地震作用下桥塔的位移和剪力地震响应的峰值包络曲线，图8给出了近断层地震动脉冲方向性对桥塔地震响应的放大系数F。从图6~8中可以看出桥塔的最大位移和最大剪力分别发生在塔顶和塔底，近断层地震动脉冲方向性对大跨度斜拉桥的地震响应有着明显的放大作用，以塔顶位移为例，东西方向、南北方向和最强脉冲方向地震作用下塔顶位移分别为137.0，162.4和199.2 cm，与东西方向和南北方向的地震记录相比，最强脉冲方向上地震作用下塔顶位移分别增大了45.4%和22.7%。同样，由图7可知，最强脉冲方向地震作用下桥塔的纵向剪力增长也非常明显，与东西方向和南北方向的地震记录相比，最强脉冲方向上地震作用下塔底剪力分别增大了27.8%和13.5%。由此说明了近断层脉冲方向性对大跨度斜拉桥桥塔地震响应有着显著的影响，最强脉冲方向地震作用下，桥塔地震响应明显要大于实际记录到的2条水平分量。

图6 桥塔纵向位移响应峰值

图7 桥塔纵向剪力响应峰值

图8 最强脉冲激励下桥塔地震响应放大系数

此外，值得注意的是随着桥塔从塔顶到塔底高度的减小，桥塔纵向剪力逐渐增大，但是在距离塔底87.26 m处突然减小了，这主要是由于该算例桥梁采用的是钻石型桥塔，在距塔底87.26 m处，桥塔分为了左右两肢，该位置以上的桥塔承受的剪力是整个桥塔产生的剪力，而从距离塔底5~87.26 m这一段剪力仅为桥塔一肢的剪力，仅相当于整个桥塔所受剪力的一半，因此桥塔剪力在距塔底87.26 m处发生了突变。

3.2 主梁地震响应

图9给出了东西方向、南北方向和最强脉冲方向3条地震作用下该算例桥梁主梁竖向位移峰值响应包络曲线，图10给出了近断层地震动脉冲方向性对主梁竖向位移响应的放大系数。从图9~10中可以看出，上述3条地震作用下主梁地震响应差异明显。类似于桥塔的地震响应，最强脉冲方向地震作用下主梁的竖向位移明显要大于东西方向和南北方向地震记录作用下主梁的位移响应。以响应最大的1/4中跨为例，相比于东西方向和南北方向的地震记录作用，最强脉冲方向上地震作用下1/4中跨主梁的竖向位移分别增大了40.23%和13.22%。同样，在其他位置处，最强脉冲方向上地震作用下桥梁结构的地震响应也明显要更大。

需要特别指出的是，不论东西方向、南北方向还是最强脉冲方向上主梁竖向位移最大值都发生在中跨跨中与桥塔之间，而中跨跨中的位移反而更小。这主要是由于该算例桥梁1阶正对称竖弯振型对应的周期为2.5 s，而1阶反对称竖弯对应的周期为1.64 s，1阶正对称竖弯所对应的周期刚好为高频地震动与长周期脉冲对反应谱产生放大效应的周期段之间，该位置处反应谱值较小，而1阶反对称竖弯对应的周期与高频段更为接近，该周期处地震动的反应谱的谱值更大，桥梁结构的1阶反对称竖弯振型被激起，因此导致了中跨的跨中位移反而比跨中与桥塔之间的主梁的竖向位移更小。

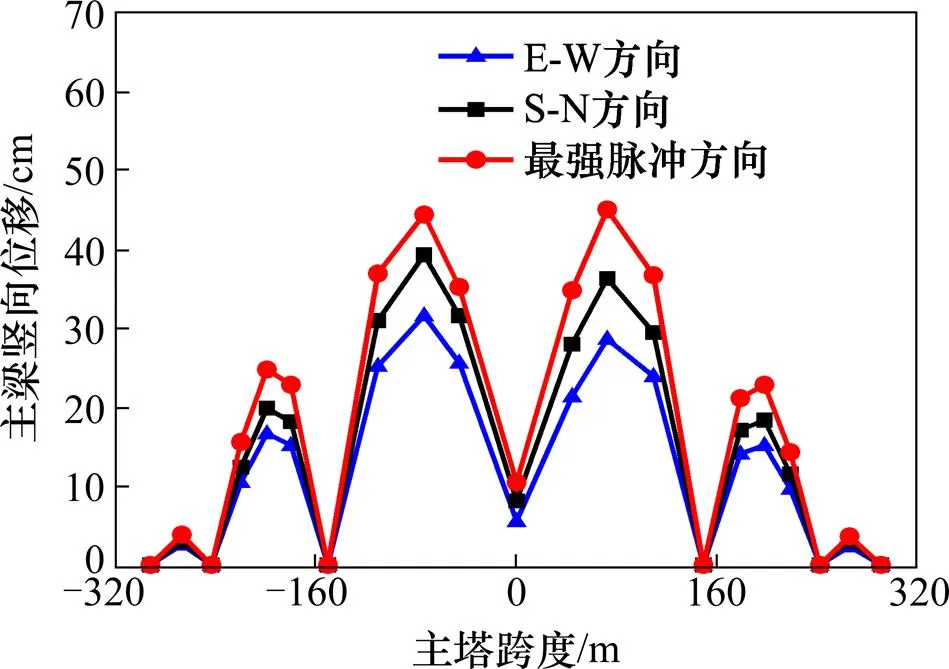
图9 主梁竖向位移响应峰值

图10 最强脉冲激励下主梁竖向位移放大系数

综上所述，可以看出近断层脉冲方向性对大跨度斜拉桥地震响应有着显著的影响，最强脉冲方向上地震动作用下，桥梁的地震响应明显要大于原始地震记录的2条水平分量作用下的结果。在桥梁地震响应分析时应该以最强脉冲方向上的地震分量作为地震输入，如果直接以实测地震记录的2条水平分量最为地震输入可能严重的低估桥梁结构的地震需求，从而导致桥梁结构的抗震设计偏于 危险。

4 结论

1) 近断层脉冲地震的峰值参数在各个方向上差异显著，1次地震中，地震动测站记录到的2条水平分量经过旋转变换后峰值加速度可能相差30%，峰值速度可能相差70%。

2) 通过连续小波变换识别处的最强脉冲方向与峰值速度PGV所在的方向基本重合，最强脉冲方向上地震动的脉冲幅值、脉冲指标以及地震动反应谱都要明显高于实测地震动的2条水平分量。

3) 近断层地震动脉冲方向性对大跨度斜拉桥地震响应有重要影响，最强脉冲方向上地震动输入时，大跨度斜拉桥地震响应明显增大，在其抗震分析时应该以最强脉冲方向上地震动作为依据，否则将低估桥梁结构的地震响应。

[1] Kalkan E, Kunnath S K. Effects of fling step and forward directivity on seismic response of buildings[J]. Earthquake Spectra, 2006, 22(2): 367−390.

[2] Somerville P G, Smith N F, Graves R W, et al. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J]. Seismological Research Letters, 1997, 68(1): 199−222.

[3] 徐艳, 黄永福, 李建中. 脉冲型地震作用下斜拉桥纵向响应的简化计算[J]. 华南理工大学学报(自然科学版), 2015, 43(2): 41−47. XU Yan, HUANG Yongfu, LI Jianzhong. Simplified calculation of longitudinal seismic response of cable-stayed bridges subjected to pulsed ground motions [J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(2): 41−47.

[4] LI S, ZHANG F, WANG J, et al. Effects of near-fault motions and artificial pulse-type ground motions on super-span cable-stayed bridge systems[J]. Journal of Bridge Engineering, 2016, 22(3): 04016128.

[5] 李帅, 王景全, 颜晓伟, 等. 近断层地震动空间分布特征对斜拉桥地震响应影响[J]. 土木工程学报, 2016, 49(6): 94−104. LI Shuai, WANG Jingquan, YAN Xiaowei, et al. Influence of spatial distribution characteristics of near-fault ground motions on seismic responses of cable-stayed bridges[J]. China Civil Engineering Journal, 2016, 49(6): 94−104.

[6] Shrestha B. Seismic response of long span cable-stayed bridge to near-fault vertical ground motions[J]. KSCE Journal of Civil Engineering, 2015, 19(1): 180−187.

[7] 常志旺. 近场脉冲型地震动的量化识别及特性研究[D].哈尔滨：哈尔滨工业大学, 2014. CHANG Zhiwang. Quantitative identification and the characteristics of near-fault pulse-like ground motions [D]. Harbin: Harbin Institute of Technology, 2014.

[8] YANG D, ZHOU J. A stochastic model and synthesis for near-fault impulsive ground motions[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(2): 243− 264.

[9] Zamora M, Riddell R. Elastic and inelastic response spectra considering near-fault effects[J]. Journal of Earthquake Engineering, 2011, 15(5): 775−808.

[10] Shahi S K, Baker J W. A probabilistic framework to include the effects of near-fault directivity in seismic hazard assessment[M]. Pacific Earthquake Engineering Research Center, 2013.

[11] 杨成, 唐泽楠, 常志旺, 等. 基于经验模态分解的速度脉冲型地震动量化识别[J]. 工程力学, 2017, 34(4): 206−212. YANG Cheng, TANG Zenan, CHANG Zhiwang, et al. EMD-based quantitative categorization for velocity pulse-like ground motions[J]. Engineering Mechanics, 2017, 34(4): 206−212.

[12] Baker J W. Quantitative classification of near-fault ground motions using wavelet analysis[J]. Bulletin of the Seismological Society of America, 2007, 97(97): 1486− 1501.

(编辑 涂鹏)

Influence of directivity of near-fault impulse effect on seismic response of long span cable stayed bridge

CHEN Zhiqiang, ZHENG Shixiong, CHEN Zhiwei, HONG Chengjing, LI Xi

(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

The impulse characteristics of near fault ground motion are obviously different in different directions. Therefore, the variability of peak ground acceleration (PGA) and peak ground velocity (PGV) in each direction was compared firstly based on typical pulse seismic record in Chi-Chi earthquake. And then the orientation of the strongest pulse is determined in terms of the wavelet transform. The difference of the impulse and pulse amplitude between the seismic wave of the strongest pulse direction and the initial earthquake record was compared. Finally, taking a large span cable stayed bridge as an example, the influence of the directional effect of near fault seismic impulse on its seismic response was studied in detail. The results show that: The PGA and PGV of the near fault pulse type ground motions are obviously different in each direction. After the rotation transformation, the variability of PGA and PGV reaches 30% and 70% respectively; The strongest pulse direction identified by continuous wavelet transform coincides with the direction of the maximum PGV value, and the response spectrum and pulse amplitude of the strong pulse direction are obviously stronger than the two horizontal components recorded by the recorded ground motion; The seismic response of long span cable stayed bridge under strong impulse direction is obviously larger than that of the two horizontal components of the actual seismic record, In the seismic analysis of long-span cable-stayed bridges in the near-fault area, the seismic action on the strongest impulse direction should be taken as input, otherwise, the displacement response of tower and girder can be underestimated by 45.4% and 40.2% respectively.

pulse directivity; continuous wavelet transform; long span cable stayed bridge; seismic response

10.19713/j.cnki.43−1423/u.2018.12.015

U442.5

A

1672 − 7029(2018)12 − 3127 − 08

2017−11−09

国家自然科学基金资助项目(U1434205)；教育部春晖计划资助项目(Z2014032)；中国铁路总公司科技开发项目(2015G002-A)

郑史雄(1965−)，男，浙江江山人，教授，博士，从事桥梁结构抗震研究；E−mail：zhengsx@home.swjtu.edu.cn